Механика несжимаемой жидкости. Основные определения и законы

1.

Механика несжимаемой
жидкости
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ЗАКОНЫ

2.

Несжимаемая жидкость
В данном разделе механики изучают законы движения
жидкости как сплошной (непрерывной) среды. Плотность
жидкости практически не зависит от давления, поэтому
жидкость будем считать несжимаемой средой, плотность
которой везде одинакова.
Для кинематического описания движения (течения)
жидкости обычно используют метод Эйлера: в
интересующей нас системе отсчета задается поле
скоростей жидкости, т. е. зависимость скорости v каждой
точки жидкости от ее радиуса-вектора r и времени t.
Во многих случаях, когда сила трения между отдельными
слоями текущей жидкости пренебрежимо мала, жидкость
можно считать идеальной (без внутреннего трения).

3.

Линии и трубки тока
Мысленно проведем в движущейся жидкости линии так,
чтобы касательные к ним в каждой точке совпадали по
направлению с вектором v. Эти линии называют линиями
тока. Линии проводят так, чтобы их густота была
пропорциональна модулю вектора v, а их направление
совпадало с направлением вектора v. Там, где скорость
больше, линии тока гуще, и наоборот.
При стационарном течении, когда v не зависит от t,
картина линий тока остается неизменной и линии тока
совпадают с траекториями частиц жидкости.
Поверхность, образованная линиями тока, которые
проведены через все точки замкнутого контура, называют
трубкой тока. При стационарном течении жидкости ее
частицы при своем движении не пересекают трубку тока.

4.

Уравнение неразрывности струи
Рассмотрим жидкость, текущую внутри
некоторой трубки тока - такой, что
скорость движения частиц жидкости
одинакова во всех точках произвольного
сечения
данной
трубки. Тогда
за
промежуток времени Δt сквозь сечение
площади S пройдет объем жидкости SvΔt.
Поскольку жидкость несжимаема, масса
жидкости между сечениями S1 и S2 трубки
тока будет оставаться неизменной. Значит, объем жидкости, протекающей
сквозь сечения S1 и S2 за время Δt, должен быть одинаковым. Отсюда
следует, что S1v1 = S2v2. Другими словами, для несжимаемой жидкости
величина Sv в любом сечении одной и той же трубки тока одинакова:
(4.1)
Это соотношение называют уравнением неразрывности струи.

5.

Уравнение Бернулли
Рассмотрим
стационарное
течение
идеальной жидкости в однородном поле
сил тяжести. Выделим часть жидкости,
которая в момент t заполняет объем
узкой трубки тока между сечениями 1 и 2.
К моменту t+Δt эта часть жидкости
переместится вдоль трубки тока в
направлении,
показанном
жирной
стрелкой, и окажется между сечениями 1'
и 2'. Приращение полной механической энергии этой части жидкости за
время Δt
(4.2)
где справа стоит работа, которую совершают силы давления (они и есть в
данном случае сторонние). При этом силы давления, перпендикулярные
выделенной трубке, работы не совершают. Работу будут совершать только
силы давления, действующие в сечениях 1 и 2. Эта работа равна

6.

в силу неразрывности струи S1Δl1 = S2Δl2
сечениями 1-1' и 2-2' одинаковы и
= ΔV, т. е. объемы между
(4.3)
Течение жидкости стационарно, поэтому полная механическая энергия
части жидкости трубки тока между сечениями 1' и 2 не меняется. Значит,
приращение энергии ΔЕ рассматриваемой части жидкости можно
представить как разность энергий элементов 2-2' и 1-1':
(4.4)
где ρ - плотность жидкости. Приравняв, согласно (4.2), выражения (4.3) и
(4.4), получим после сокращения на ΔV и перегруппировки слагаемых
следующее уравнение:
Так как сечения 1 и 2 взяты произвольно, то
(4.5)
где все величины относятся к одной и той же линии тока. Для разных
линий тока эта константа, вообще говоря, будет своей.
Уравнение (4.5) называют уравнением Бернулли. Несмотря на то, что это
уравнение получено для идеальной жидкости, оно достаточно хорошо
выполняется и для реальных жидкостей, внутреннее трение которых
(вязкость) сравнительно мало.

7.

Вязкость
Всем реальным жидкостям в той или иной степени присуще внутреннее
трение, или вязкость. Рассмотрим движение жидкости, скорость v
отдельных слоев которой зависит только от поперечной координаты z.
Сила трения Fтр, действующая между слоями движущейся жидкости,
может быть представлена следующей формулой:
(4.6)
где η - коэффициент внутреннего
трения, или вязкость - величина,
зависящая от природы и состояния
жидкости; ∂v/∂z - градиент модуля
скорости (он характеризует крутизну
графика зависимости v от z); S площадь
интересующей
нас
поверхности раздела между слоями
(эта поверхность перпендикулярна оси
z).

8.

Ламинарное и турбулентное течения.
Особенностью ламинарного течения является его регулярность. При
ламинарном течении в прямолинейной трубе частицы жидкости
движутся вдоль траекторий, параллельных оси трубы. При больших
скоростях ламинарное течение становится неустойчивым и переходит в
турбулентное, при котором частицы жидкости совершают беспорядочные
движения, что приводит к перемешиванию между слоями жидкости.
Такие быстрые и нерегулярные изменения происходят вследствие
неустойчивости ламинарных течений при определенных условиях.
Характер течения зависит от значения безразмерной величины – числа
Рейнольдса:
(4.7)
где ρ - плотность жидкости, v - характерная скорость потока, l
характерный размер, η - вязкость. При малых значениях числа Re
наблюдается ламинарное течение, а начиная с некоторого критического
значения Re, ламинарное течение переходит в турбулентное. Если в
качестве характерного размера для круглой трубы, взять ее радиус, то
критическое значение Re ~ 1000 (для воды).

9.

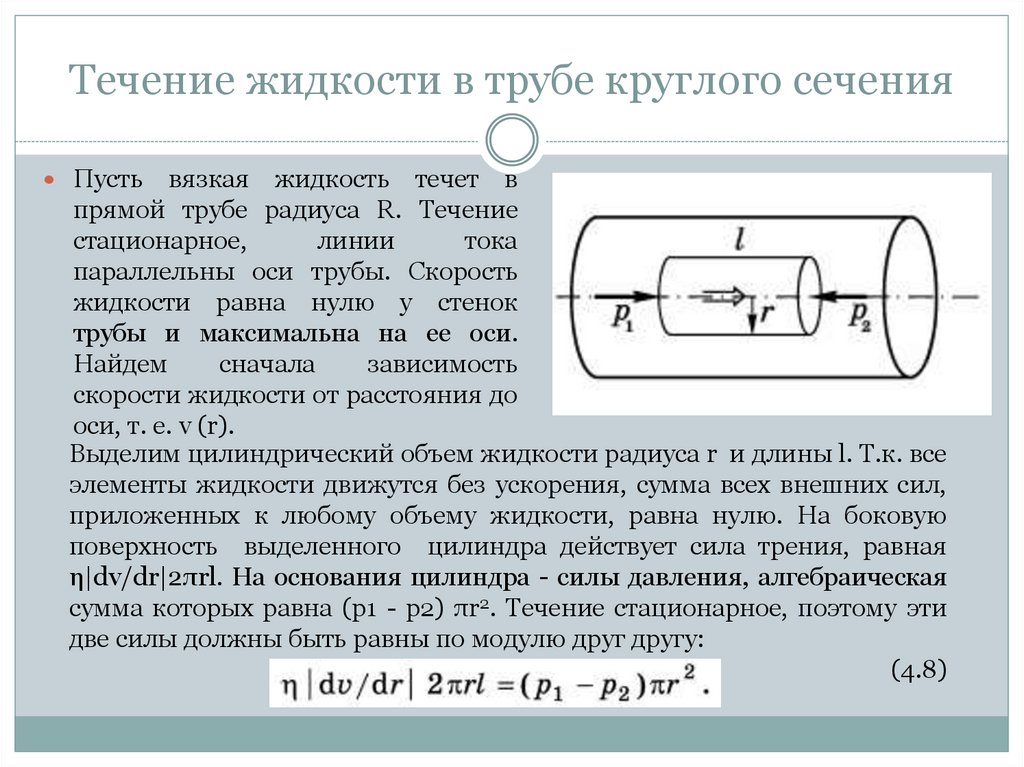
Течение жидкости в трубе круглого сечения
Пусть
вязкая жидкость течет в
прямой трубе радиуса R. Течение
стационарное,
линии
тока
параллельны оси трубы. Скорость
жидкости равна нулю у стенок
трубы и максимальна на ее оси.
Найдем
сначала
зависимость
скорости жидкости от расстояния до
оси, т. е. v (r).
Выделим цилиндрический объем жидкости радиуса r и длины l. Т.к. все
элементы жидкости движутся без ускорения, сумма всех внешних сил,
приложенных к любому объему жидкости, равна нулю. На боковую
поверхность выделенного цилиндра действует сила трения, равная
η|dv/dr|2πrl. На основания цилиндра - силы давления, алгебраическая
сумма которых равна (p1 - p2) πr2. Течение стационарное, поэтому эти
две силы должны быть равны по модулю друг другу:
(4.8)

10.

Скорость v уменьшается с ростом расстояния r от оси трубы, поэтому dv/dr <0
и |dv/dr| =-dv/dr. Тогда уравнение (4.8) можно переписать так:
Интегрируем его с учетом того, что у стенок, где r = R, v = 0 :
В результате получим:
(4.9)
График этой зависимости v(r) будет иметь вид, представленный на рисунке.
Найдем поток Q жидкости, т. е. объем
жидкости,
протекающей
через
поперечное сечение трубы за единицу
времени. Объем жидкости, ежесекундно
протекающей
через
элементарное
кольцо радиуса (r, r+dr), dQ = v·2πrdr.
Подставив v(r) из (4.9) и интегрируя по
r, найдем
(4.10)
Это формула Пуазейля.