Similar presentations:
Метод координат (9 класс)
1. Метод координат
МЕТОДКООРДИНАТ
Выполнила: ученица 9В класса
Средней школы №31
Борисова Дарья
Учитель: Кутина Т.А.
г. Братск
2. П 89 Разложение вектора по двум неколлинеарным векторам.
П 89 РАЗЛОЖЕНИЕВЕКТОРА ПО ДВУМ
НЕКОЛЛИНЕАРНЫМ
ВЕКТОРАМ.
3.
ЛеммаЕсли векторы а и в коллинеарны и а=0,то
существует такое число к, что в=ка .
a b
k b
k a
2.
k 0 b ka
a b
и
b ka
b
k k 0 b ka
a
и
b ka
Из пункта 1 и 2 следует, что
b
b a
ka a
b
a
a
b a
ka
a 1
b ka
b
4.
Теоремаp
Любой вектор
можно разложить
по двум
неколлинеарным векторам a и b ,причем
коэффициенты разложения определяются
единственным образом.
a
и b
Пусть
неколлинеарны (не
являются параллельными и не 0 )
p xa yb
5.
вектор p1.Докажем,что любой
можно
разложить
по двум неколлинеарным векторам a
и b
Доказательство.
p
a
1) p o ; p oa ob
О
b
2) p // b p kb
p o a k b
3) p // a p // b
A
P
PA// b
OAPB- //-мм
PB//
a
p
a
О
b
OP=OA+OB
B
p xa yb
; ОA=x a
OB=y b
по Лемме
6.
П 90 Координаты вектораy
i
;
Ox
;
j Oy
j1
x
1
i
i не //
{ х ; y}
x ; y – координаты
и
- единичные
векторы
j p xi yj
x и y- коэффициенты
p
i
iи j
i 1
j 1
j
p
- координатные векторы
p xi yj
x ; y – координаты
p
7.
Правила действий над векторами сзаданными координатами.
Равные векторы имеют
равные координаты
m
y
m 4i 3 j
p
m {4 ;3}
m p
х
p 4i 3 j
Координаты вектора p - это коэффициенты
разложения этого вектора по
i
и
j
.
8.
1.Пусть
а х1 ; у1
b х2 ; у 2
a х1 i; у1 j
a b
b х2 i; у 2 j
, тогда
a b 0
a b х1 i y1 j x2 i y2 j
x1 x2 i y1 y2 j 0 i 0 j 0
Следовательно,
х1 = х2; у1 = у2
9.
Каждая координата суммы двух (и более)векторов равна сумме соответствующих
координат этих векторов.
Дано:
а х1 ; у1
b х2 ; у 2
Доказать:
Док-во:
с a b
с х1 х2 ; у1 у 2
a х1 i; у1 j
b х i; у j
2
2
a b х1 i y1 j x2 i y 2 j
x1 x2 i y1 y2 j с
Следовательно,
с х1 х2 ; у1 у2
10.
Координаты противоположныхвекторов противоположны.
Пусть p { х ; y}
p xi yj
p xi yj
p { -х ; -y}
11.
Координаты разности двух векторовравны разности соответствующих
координат вычитаемых векторов.
Дано:
а х1 ; у1
b х2 ; у 2
Доказать:
Док-во:
с a b
с х1 х2 ; у1 у 2
a х1 i; у1 j
b х i; у j
2
2
a b х1 i y1 j x2 i y2 j
x1 x2 i y1 y2 j с
Следовательно,
с х1 х2 ; у1 у2
12.
Координаты коллинеарных векторовпропорциональны.
a {x1 ; y1}
ka {kx1 ; ky1}
{0;0}
o
y
A (x ; y)
yA
O
xA
x
OA { х ; y}
A (x ; y) OA
{ х ; y}
Координаты p-вектора численно равны координатам
точки, являющейся концом этого вектора.







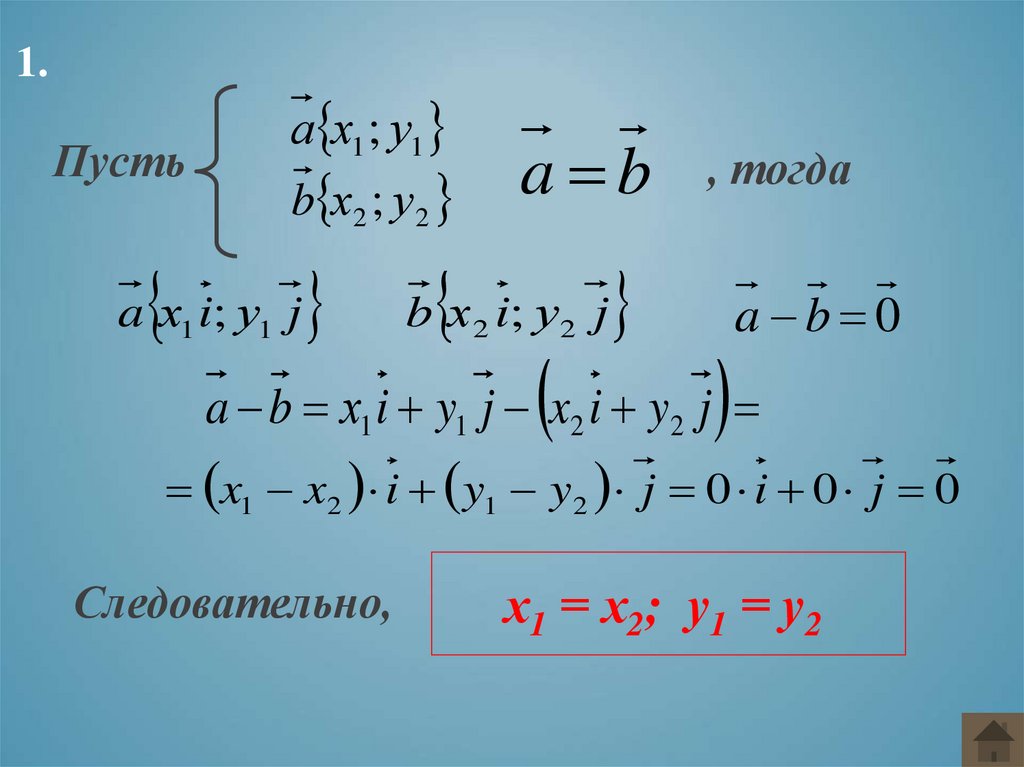




 physics
physics








