Similar presentations:
²êÆÜøðàÜ ØºøºÜ²Üºð
1. ²êÆÜøðàÜ ØºøºÜ²Üºð
ÀܸвÜàôð¾ÈºÎîð²îºÊÜÆβ
²êÆÜøðàÜ ØºøºÜ²Üºð
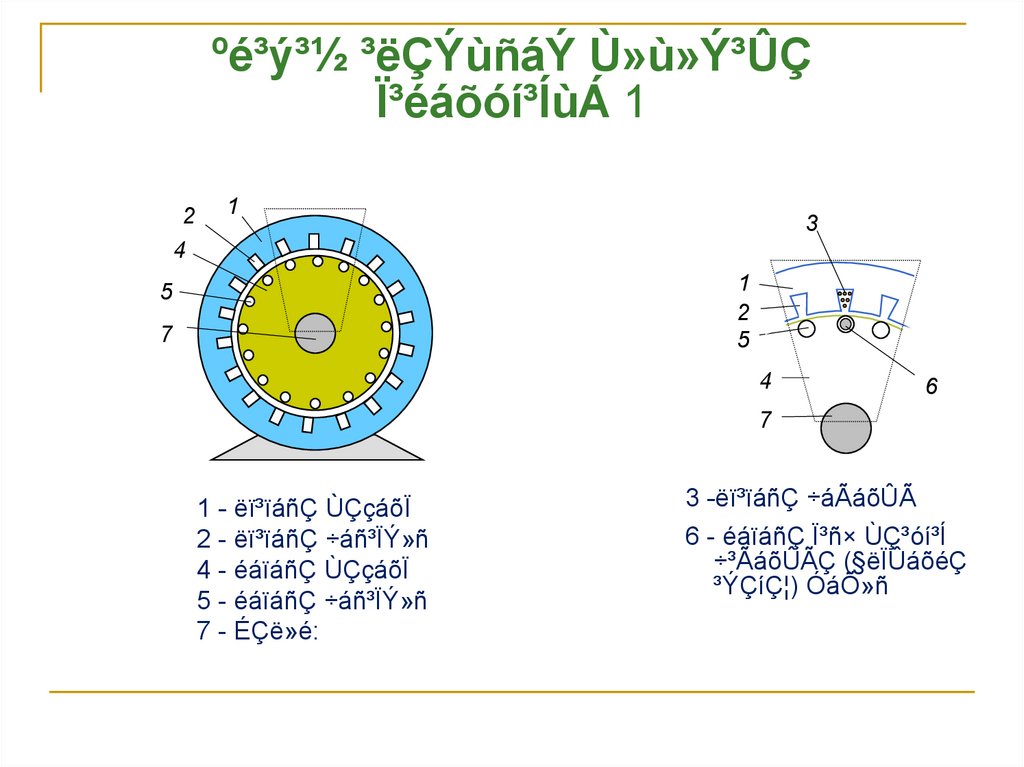
2. ºé³ý³½ ³ëÇÝùñáÝ Ù»ù»Ý³ÛÇ Ï³éáõóí³ÍùÁ 1
24
1
3
1
2
5
5
7
4
6
7
1 - ëï³ïáñÇ ÙÇçáõÏ
2 - ëï³ïáñÇ ÷áñ³ÏÝ»ñ
4 - éáïáñÇ ÙÇçáõÏ
5 - éáïáñÇ ÷áñ³ÏÝ»ñ
7 - ÉÇë»é:
3 -ëï³ïáñÇ ÷áÃáõÛÃ
6 - éáïáñÇ Ï³ñ× Ùdzóí³Í
÷³ÃáõÛÃÇ (§ëÏÛáõéÇ
³ÝÇíǦ) ÓáÕ»ñ
3. ºé³ý³½ ³ëÇÝùñáÝ Ù»ù»Ý³ÛÇ Ï³éáõóí³ÍùÁ 2
ü³½³ÛÇÝ éáïáñáí ³ëÇÝùñáÝß³ñÅÇãÇ éáïáñÇ Ï³éáõóí³ÍùÁ (ա)
¨ å³ÛÙ³Ý³Ï³Ý Ýß³ÝÁ (բ)
5
4
8
7
ա)
բ)
γñ× Ùdzóí³Í éáïáñáí
³ëÇÝùñáÝ ß³ñÅÇãÇ éáïáñÇ
ÃÙµáõϳӨ ÷³ÃáõÛÃÁ
(§սÏÛáõéÇ ³ÝÇíÁ¦) (ա) ¨
å³ÛÙ³Ý³Ï³Ý Ýß³ÝÁ (բ)
R
ա)
9
4 - éáïáñÇ ÙÇçáõÏ
5 - éáïáñÇ ÷áñ³ÏÝ»ñ
7 - ÉÇë»é
8 – åÕÝÓ» ûÕ³ÏÝ»ñ
9 - ·ñ³ýÇï» (³ÍË» ûÕ³ÏÝ»ñ)
բ)
4. äïïíáÕ Ù³·ÝÇë³Ï³Ý ¹³ßïÇ ëï³óáõÙÁ 1
xA
2 /3
Y
2 /3
+ B
C
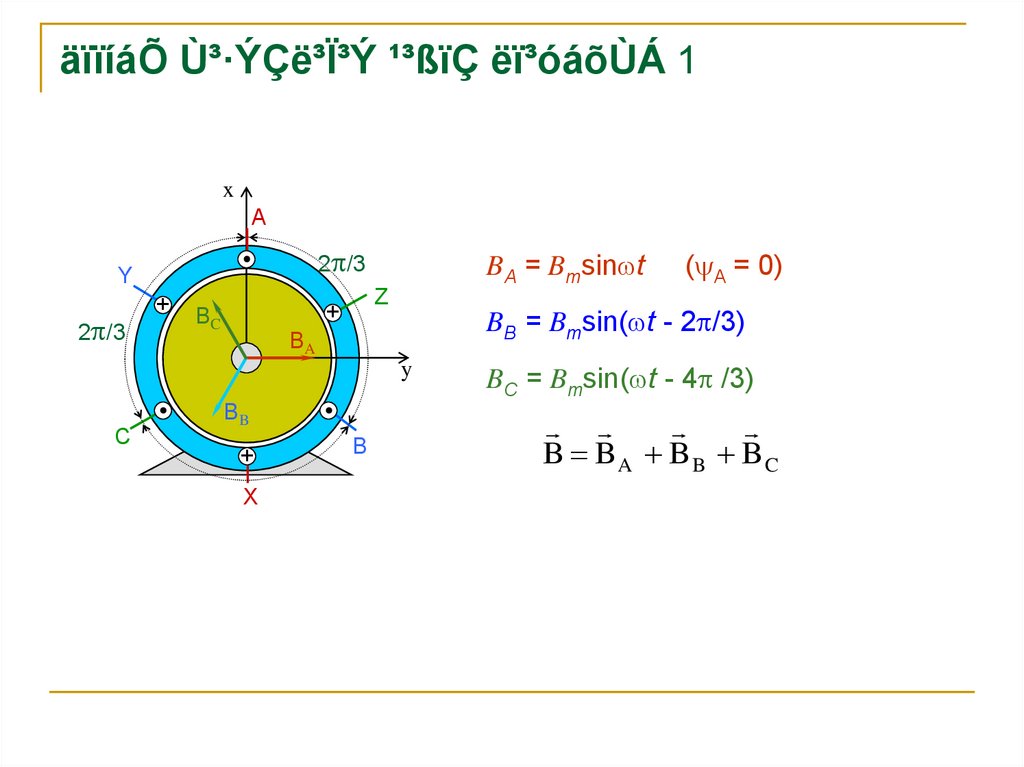
BA = Bmsin t
Z
+
BB = Bmsin( t - 2 /3)
BA
y
C
BB
+
X
( A = 0)
B
BC = Bmsin( t - 4 /3)
B B A B B BC
5. äïïíáÕ Ù³·ÝÇë³Ï³Ý ¹³ßïÇ ëï³óáõÙÁ 2
11
Bx BA BB cos( 1200 ) BC cos 1200 BA BB ( ) BC ( )
2
2
Y
1200
-1200
X
1
2 1
4
Bx Bm sin t sin( t ) sin( t ) 1.5Bm cos t
2
3
2
3
B y BA sin 00 BB sin( 1200 ) BC sin 1200 BB (
3
3
) BC
2
2
3
2
3
4
B y Bm
sin( t )
sin( t ) 1.5 Bm sin t
2
3
2
3
6. äïïíáÕ Ù³·ÝÇë³Ï³Ý ¹³ßïÇ ëï³óáõÙÁ 3
YBC
B y2
1.5Bm
By
t
α
BA
BB
B
ω
Bx2
Bx
X
n1
60 f 1 (åï/ñ)
p
tg
B x sin t
tg t
B y cos t
P – ½áõÛ· µ¨»éÝ»ñÇ
ÃÇí
êÇÝËñáÝ ³ñ³·áõÃÛáõÝÝ»ñÇ ë³Ý¹Õ³ÏÁ
P = 1; 2; 3; 4
P = 1, n1 = 3000 (åï/ñ),
P = 2, n1 = 1500 (åï/ñ),
P = 3, n1 = 1000 (åï/ñ),
P = 4, n1 = 7500 (åï/ñ):
7. ²ëÇÝùñáÝ ß³ñÅÇãÇ ³ß˳ï³ÝùÇ ëϽµáõÝùÁ
ëï e2 i2 F Mn1
êï³ïáñ
F
F
èáïáñ
ëï
F
n2
n2 = const < n1
n1 n 2
- ë³ÑùÇ ·áñͳÏÇó
s
n1
60 f
n2 n1 (1 s)
(1 s)
p
²Ýí³Ý³Ï³Ý µ»éÝí³ÍùÝ»ñÇ ¹»åùáõÙ` s³ = 0,02…0,06 .
»Ã» n1 = 3000 åï/ñ, n2³ = (2820 … 2940) åï/ñ
n1 = 1500 åï/ñ, n2³ = (1410 … 1470) åï/ñ
n1 = 1000 åï/ñ, n2³ = (940 … 980) åï/ñ
n1 = 750 åï/ñ, n2³ = (705 … 735) åï/ñ
ä³ñ³å ÁÝóóùÇ ¹»åùáõÙ` s0 = 0,005…0,01:
8. ²ëÇÝùñáÝ Ù»ù»Ý³ÛÇ ³ß˳ï³Ýù³ÛÇÝ é»ÅÇÙÝ»ñÁ
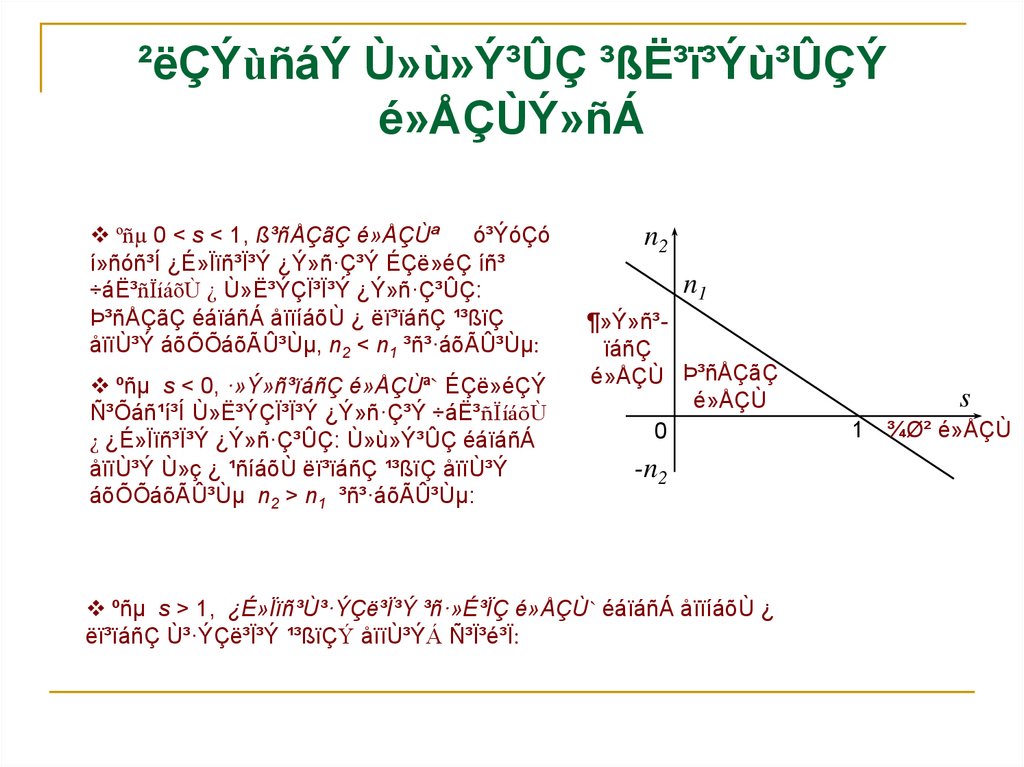
ºñµ 0 < s < 1, ß³ñÅÇãÇ é»ÅÇÙªó³ÝóÇó
í»ñóñ³Í ¿É»Ïïñ³Ï³Ý ¿Ý»ñ·Ç³Ý ÉÇë»éÇ íñ³
÷á˳ñÏíáõÙ ¿ ٻ˳ÝÇÏ³Ï³Ý ¿Ý»ñ·Ç³ÛÇ:
Þ³ñÅÇãÇ éáïáñÁ åïïíáõÙ ¿ ëï³ïáñÇ ¹³ßïÇ
åïïÙ³Ý áõÕÕáõÃÛ³Ùµ, n2 < n1 ³ñ³·áõÃÛ³Ùµ:
ºñµ s < 0, ·»Ý»ñ³ïáñÇ é»ÅÇÙª` ÉÇë»éÇÝ
ѳÕáñ¹í³Í ٻ˳ÝÇÏ³Ï³Ý ¿Ý»ñ·Ç³Ý ÷á˳ñÏíáõÙ
¿ ¿É»Ïïñ³Ï³Ý ¿Ý»ñ·Ç³ÛÇ: Ù»ù»Ý³ÛÇ éáïáñÁ
åïïÙ³Ý Ù»ç ¿ ¹ñíáõÙ ëï³ïáñÇ ¹³ßïÇ åïïÙ³Ý
áõÕÕáõÃÛ³Ùµ n2 > n1 ³ñ³·áõÃÛ³Ùµ:
n2
n1
¶»Ý»ñ³ïáñÇ
é»ÅÇÙ Þ³ñÅÇãÇ
é»ÅÇÙ
0
-n2
ºñµ s > 1, ¿É»Ïïñ³Ù³·ÝÇë³Ï³Ý ³ñ·»É³ÏÇ é»ÅÇÙ` éáïáñÁ åïïíáõÙ ¿
ëï³ïáñÇ Ù³·ÝÇë³Ï³Ý ¹³ßïÇÝ åïïÙ³ÝÁ ѳϳé³Ï:
s
1 ¾Ø² é»ÅÇÙ
9. ²ëÇÝùñáÝ ß³ñÅÇãÇ ³ß˳ï³ÝùÁ µÝáõó·ñáÕ ³Ýí³Ý³Ï³Ý å³ñ³Ù»ïñ»ñÁ 1
P³ - ²ëÇÝùñáÝ ß³ñÅÇãÇ ³Ýí³Ý³Ï³Ý ѽáñáõÃÛáõÝÁ ÉÇë»éÇ íñ³ ½³ñ·³óñ³Íٻ˳ÝÇÏ³Ï³Ý Ñ½áñáõÃÛáõÝÝ ¿ ³Ýí³Ý³Ï³Ý µ»éÝí³ÍùÇ ¹»åùáõÙ:
P³ ³Ýí³Ý³Ï³Ý ѽáñáõÃÛ³Ùµ »ñϳñ³ï¨ ³ß˳ï»ÉÇë ß³ñÅÇãÇ
ç»ñÙ³ëïÇ׳ÝÁ ãÇ ·»ñ³½³ÝóáõÙ ÃáõÛɳïñ»ÉÇ ë³ÑٳݳÛÇÝ ³ñÅ»ùÁ:
P¿..³ 3U ³ I ³ cos ³ - ²ëÇÝùñáÝ ß³ñÅÇãÇ ëå³éÙ³Ý Ñ½áñáõÃÛáõÝÁ`
ß³ñÅÇãÇ í»ñóñ³Í ¿É»Ïïñ³Ï³Ý ѽáñáõÃÛáõÝÁ
³Ýí³Ý³Ï³Ý µ»éÝí³ÍùÇ ¹»åùáõÙ;
³
P³
0,8 0,95 -²ëÇÝùñáÝ ß³ñÅÇãÇ û·ï³Ï³ñ ·áñÍáÕáõÃÛ³Ý
P¿.³
·áñͳÏÇóÁ ³Ýí³Ý³Ï³Ý µ»éÝí³ÍùÇ ¹»åùáõÙ;
P³ = P¿.³ - P³ - ²ëÇÝùñáÝ ß³ñÅÇãÇ Ñ½áñáõÃÛ³Ý ÏáñáõëïÝ»ñÁ
³Ýí³Ý³Ï³Ý µ»éÝí³ÍùÇ ¹»åùáõÙ:
10. ²ëÇÝùñáÝ ß³ñÅÇãÇ ³ß˳ï³ÝùÁ µÝáõó·ñáÕ ³Ýí³Ý³Ï³Ý å³ñ³Ù»ïñ»ñÁ 2
ºé³ý³½ ß³ñÅÇãÁ ϳñáÕ ¿ ³ß˳ï»É »ñÏáõ ï³ñµ»ñ ·Í³ÛÇÝ ³Ýí³Ý³Ï³ÝɳñáõÙÝ»ñáí.
U³ ·Í³ÛÇÝ É³ñáõÙáí` »Ã» ß³ñÅÇãÇ ëï³ïáñÇ ÷³ÃáõÛÃÁ Ùdzóí³Í ¿
³ëïÕ³Ó,
U³
·Í³ÛÇÝ É³ñáõÙáí` »Ã» ß³ñÅÇãÇ ëï³ïáñÇ ÷³ÃáõÛÃÁ
3
Ùdzóí³Í ¿ »é³ÝÏÛáõݳӨ:
cos ³ 0,8 0,9 - ß³ñÅÇãÇ Ñ½áñáõÃÛ³Ý ·áñͳÏÇóÁ ³Ýí³Ý³Ï³Ý
µ»éÝí³ÍùÇ ¹»åùáõÙ
cos 0 0,1 0,2 - ß³ñÅÇãÇ Ñ½áñáõÃÛ³Ý ·áñͳÏÇóÁ å³ñ³å
ÁÝóóùÇ é»ÅÇÙáõÙ
11. ²ëÇÝùñáÝ ß³ñÅÇãÇ ³ß˳ï³ÝùÁ µÝáõó·ñáÕ ³Ýí³Ý³Ï³Ý å³ñ³Ù»ïñ»ñÁ 3
ºé³ý³½ ³ëÇÝùñáÝ ß³ñÅÇãÇ ³Ýí³Ý³Ï³Ý Ñáë³ÝùÁI³
P¿.³
3 U ³ cos ³
P³
3 U ³ ³ cos ³
²ëÇÝùñáÝ ß³ñÅÇãÇ éáïáñÇ ³Ýí³Ý³Ï³Ý ³ñ³·áõÃÛáõÝÁ ¨ ë³ÑùÁ
n 2³ n1 (1 s³ )
s³
n1 n2³
100% (2 6)%
n1
ÈÇë»éÇ íñ³ ³ëÇÝùñáÝ ß³ñÅÇãÇ ½³ñ·³óñ³Í ³Ýí³Ý³Ï³Ý ÙáÙ»ÝïÁ
M³
P³
60 P³
2³
2 n2³
12. ²ëÇÝËñáÝ ß³ñÅÇãÇ Ñ½áñáõÃÛáõÝÝ»ñÇ Ñ³ßí»ÏßÇéÁ
P1P1 3UI cos
P1¹
P1ÙÇç
P¿Ù
P¿Ù
P1÷³Ã
PÙ = P¿Ù – P2÷ =
PÙ»Ë
P2
P2
P2
P1
P¿Ù = P1¹ P1ÙÇç
P2÷
PÙ»Ë
= P1 – P1÷ – P1ÙÇç – P2÷³Ã
P2 = PÙ»Ë – Pß÷
P1 P2 = Pß = P1÷³Ã + P1ÙÇç + P2÷³Ã + PÙ»Ë
13. ²ëÇÝùñáÝ ß³ñÅÇãÇ Ù»Ë³ÝÇÏ³Ï³Ý µÝáõó·ÇÍÁ
sÏñn1 n 2Ïñ
n1
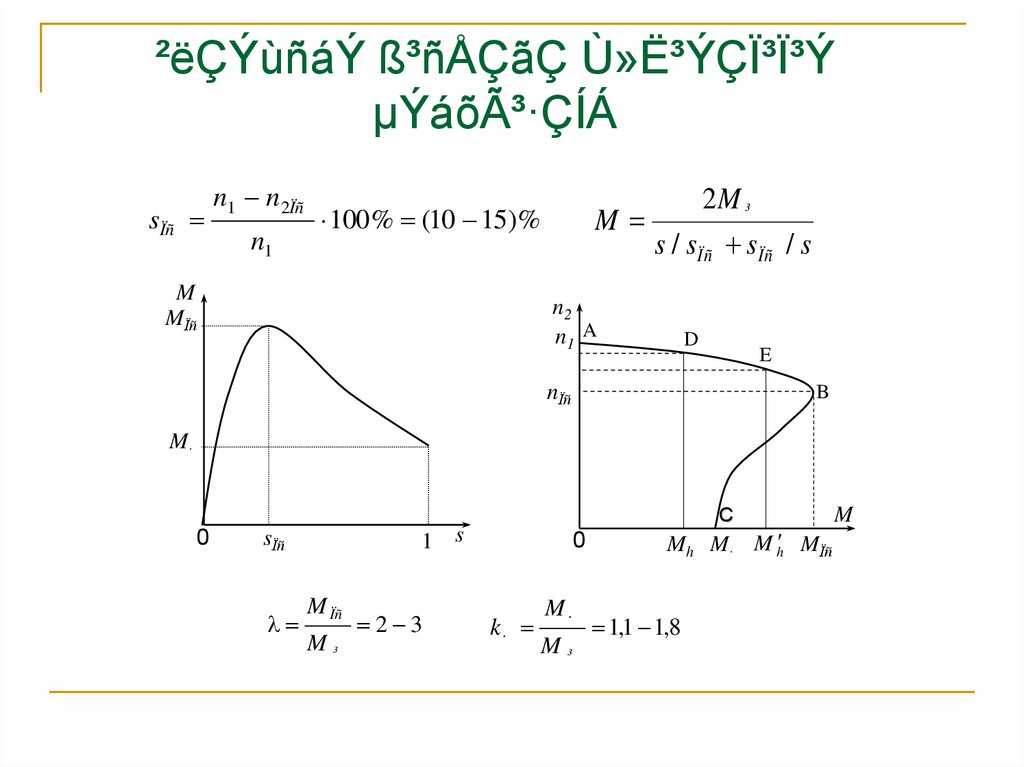
2M ³
M
s / sÏñ sÏñ / s
100 % (10 15)%
M
MÏñ
n2
n1 A
D
E
nÏñ
B
M·
C
0
1 s
sÏñ
M Ïñ
M³
2 3
0
k·
M·
M³
Mh M· M h MÏñ
1,1 1,8
M
14. êÝáÕ ó³ÝóÇ É³ñÙ³Ý ³½¹»óáõÃÛáõÝÁ ³ëÇÝùáÝ ß³ñÅÇãÇ ³ß˳ï³ÝùÇ íñ³
n2n1 A
U2
U1
U³
U3
M = f(U) ,
nÏñ f(U)
U1 = (0,8 – 0,9)U³
nÏñ
U2 = (0,6 – 0,7)U³
M
0
M·1
M·
Mh
U3 = (1,1 – 1,2)U³
MÏñ1 MÏñ
êÝáÕ ó³ÝóÇ É³ñÙ³Ý ß»ÕÙ³Ý ÃáõÛɳïñ»ÉÇ ë³ÑÙ³ÝÝ»ñÁ ³ëÇÝùáÝ
ß³ñÅÇãÇ ÝáñÙ³É ³ß˳ï³ÝùÇ Ñ³Ù³ñ
5% < U < +5% (+10%)
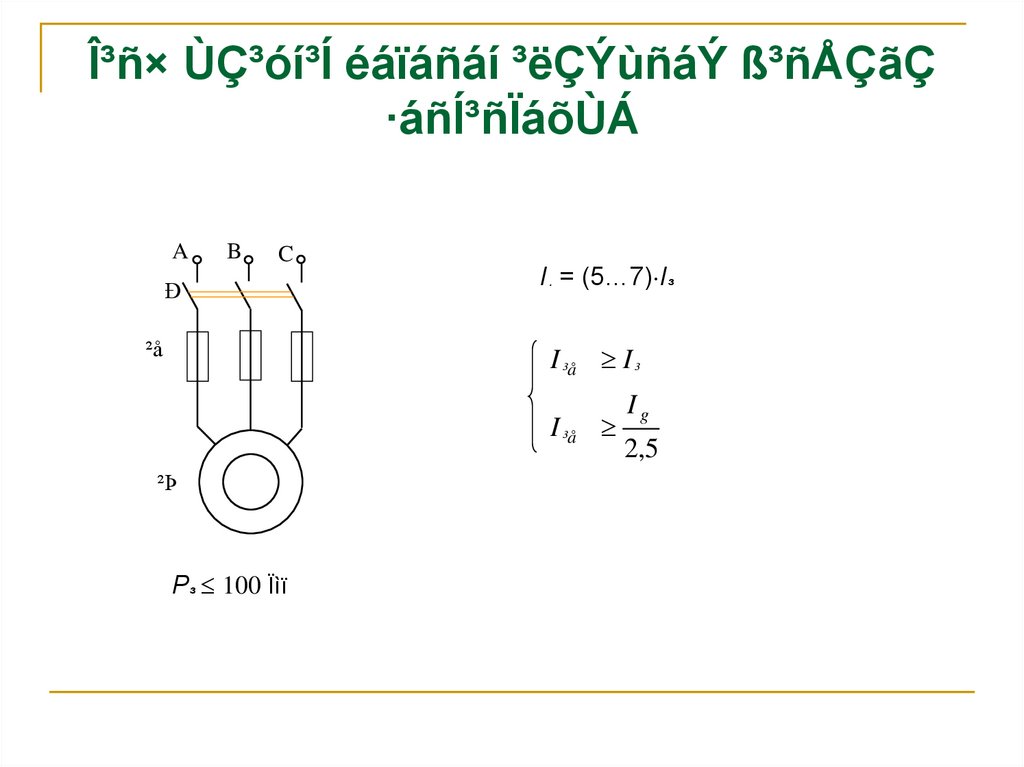
15. γñ× Ùdzóí³Í éáïáñáí ³ëÇÝùñáÝ ß³ñÅÇãÇ ·áñͳñÏáõÙÁ
AB
C
Ð
²å
I· = (5…7) I³
I ³å I ³
I ³å
²Þ
P³ 100 Ïìï
Ig
2,5
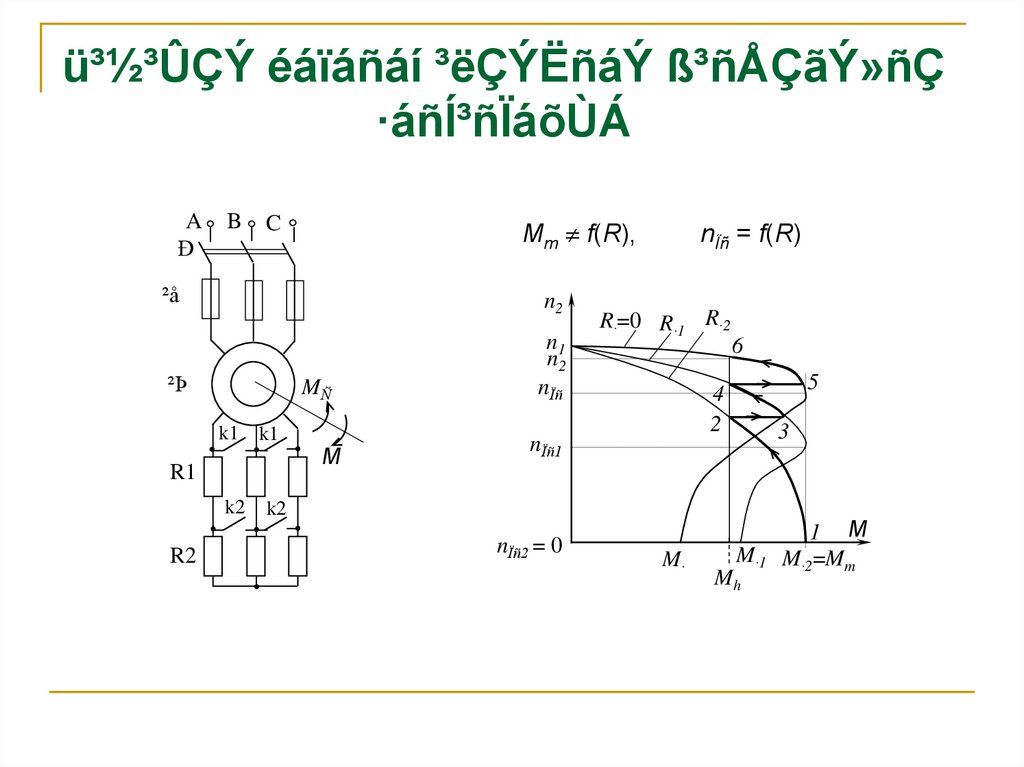
16. ü³½³ÛÇÝ éáïáñáí ³ëÇÝËñáÝ ß³ñÅÇãÝ»ñÇ ·áñͳñÏáõÙÁ
AÐ
B
C
Mm f(R),
²å
n2
²Þ
MÑ
k1
k1
M
R1
k2
R2
n1
n2
nÏñ
nÏñ = f(R)
R·=0 R·1 R·2
6
5
4
2
nÏñ1
3
k2
nÏñ2 = 0
M·
M·1
Mh
1 M
M·2=Mm
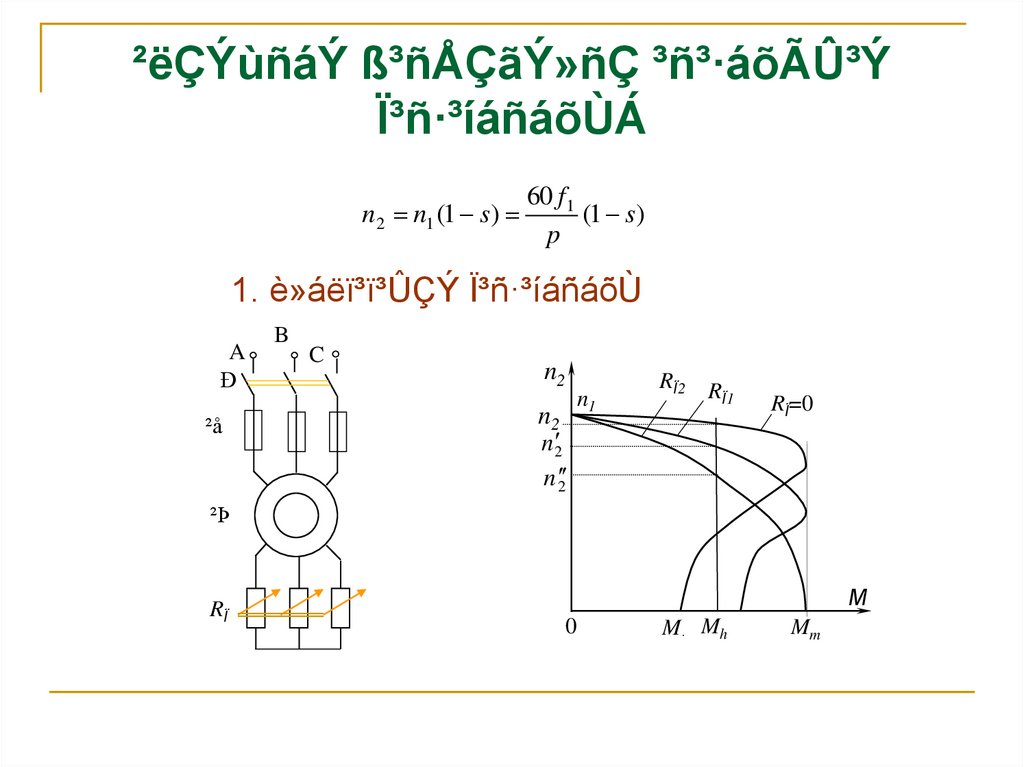
17. ²ëÇÝùñáÝ ß³ñÅÇãÝ»ñÇ ³ñ³·áõÃÛ³Ý Ï³ñ·³íáñáõÙÁ
n2 n1 (1 s)60 f1
(1 s)
p
1. è»áëï³ï³ÛÇÝ Ï³ñ·³íáñáõÙ
A
Ð
²å
B
C
n2
n1
n2
RÏ2 R
Ï1
RÏ=0
n 2
n 2
²Þ
RÏ
M
0
M · Mh
Mm
18. ²ëÇÝùñáÝ ß³ñÅÇãÝ»ñÇ ³ñ³·áõÃÛ³Ý Ï³ñ·³íáñáõÙÁ
2. ´¨»é³ÛÇÝ Ï³ñ·³íáñáõÙN
I
+
A
.
S
X
+
S
.
I
N
I
+
N
P = 2, n1 = 1500 åï/ñ
.
I
I
A
.
+
S
P = 1, n1 = 3000 åï/ñ
X
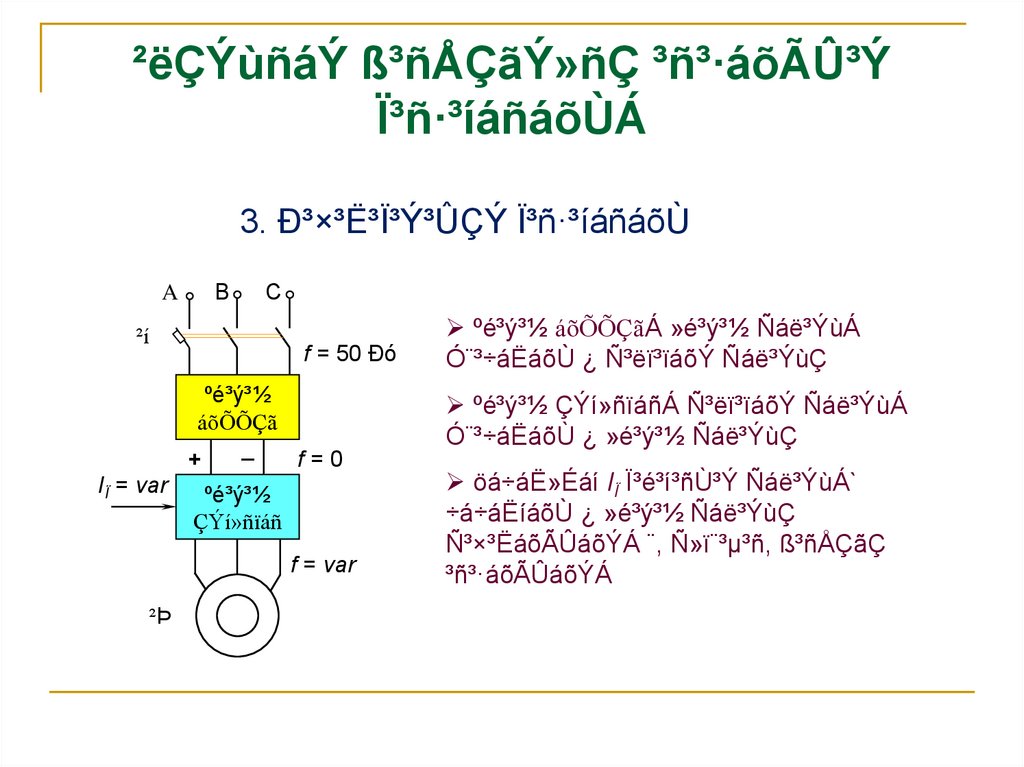
19. ²ëÇÝùñáÝ ß³ñÅÇãÝ»ñÇ ³ñ³·áõÃÛ³Ý Ï³ñ·³íáñáõÙÁ
3. г׳˳ϳݳÛÇÝ Ï³ñ·³íáñáõÙA
B
C
²í
f = 50 Ðó
ºé³ý³½
áõÕÕÇã
_
+
f=0
IÏ = var
ºé³ý³½
ÇÝí»ñïáñ
f = var
²Þ
ºé³ý³½ áõÕÕÇãÁ »é³ý³½ Ñáë³ÝùÁ
Ó¨³÷áËáõÙ ¿ ѳëï³ïáõÝ Ñáë³ÝùÇ
ºé³ý³½ ÇÝí»ñïáñÁ ѳëï³ïáõÝ Ñáë³ÝùÁ
Ó¨³÷áËáõÙ ¿ »é³ý³½ Ñáë³ÝùÇ
öá÷áË»Éáí IÏ Ï³é³í³ñÙ³Ý Ñáë³ÝùÁ`
÷á÷áËíáõÙ ¿ »é³ý³½ Ñáë³ÝùÇ
ѳ׳ËáõÃÛáõÝÁ ¨, ѻ勉µ³ñ, ß³ñÅÇãÇ
³ñ³·áõÃÛáõÝÁ











 medicine
medicine


