Similar presentations:
Преобразования координат на плоскости
1. Преобразования координат на плоскости
2. Пример
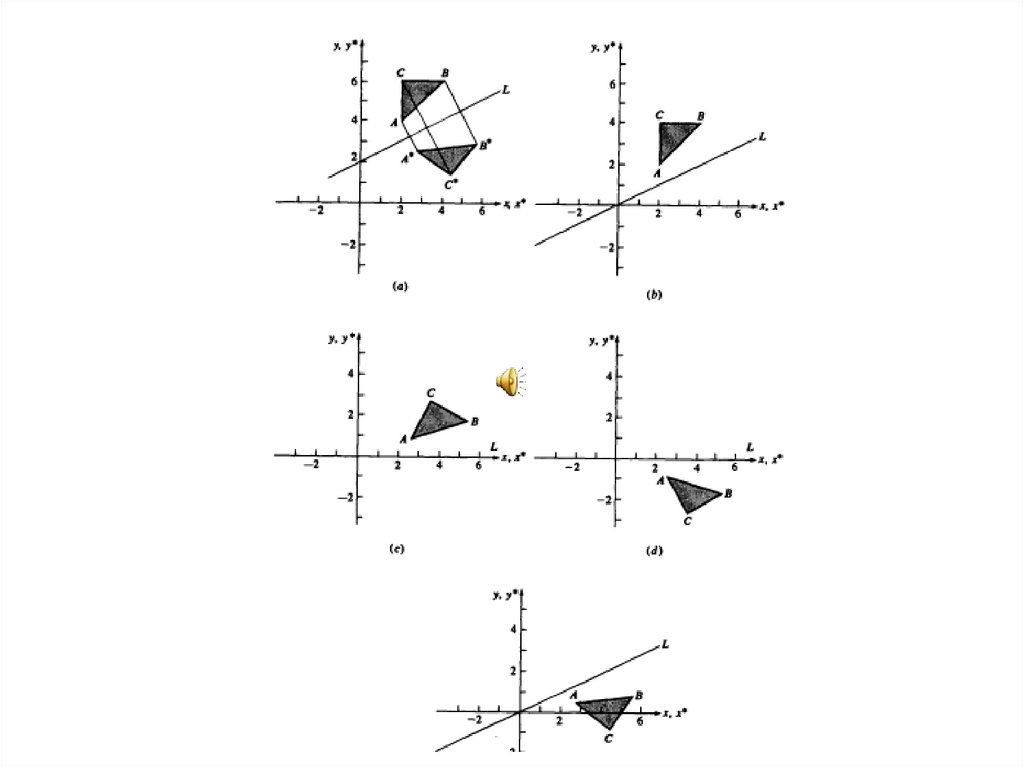
Рассмотрим прямую y=0.5(x+4) итреугольник АВС, где А(2,4,1), В(4,6,1),
С(2,6,1). Найти координаты треугольника,
симметричного заданному относительно
данной прямой.
Роджерс, Адамс. С.76-105 (С.101-105)
3.
4.
Матрица перемещени яПереместим прямую до совпадения с началом координат
1 0 0
S 0 1 0
0 2 1
x
*
y * 1 x
x* x
y* y 2
1 0 0
y 1 0 1 0
0 2 1
5.
Матрица поворотаcosα sin α 0
V - sin α cosα 0 , против часовой стрелки
0
0
1
cosα - sin α 0
V sin α cosα 0 , по часовой стрелки
0
0
1
1
2
arctg 26.57
2 / 5 1/ 5 0
**
**
*
*
x y 1 x y 1 1/ 5 2 / 5 0
0
0
1
2 * 1 * **
1 * 2 *
**
x
x
y ,y
x
y
5
5
5
5
6.
Матрица отражения относительно оси Х1 0 0
R 0 -1 0
0 0 1
x
***
y
x x
***
y
***
***
**
y
**
1 x
**
y
**
1 0 0
1 0 - 1 0
0 0 1
7.
Обратные матрицы2 / 5 1/ 5 0
V 1 1 / 5 2 / 5 0
0
0
1
1 0 0
1
S 0 1 0
0 2 1
Результирующая матрица
4 / 5 0
3/ 5
1
1
T S V R V S 4 / 5 3 / 5 0
8 / 5 16 / 5 1
8.
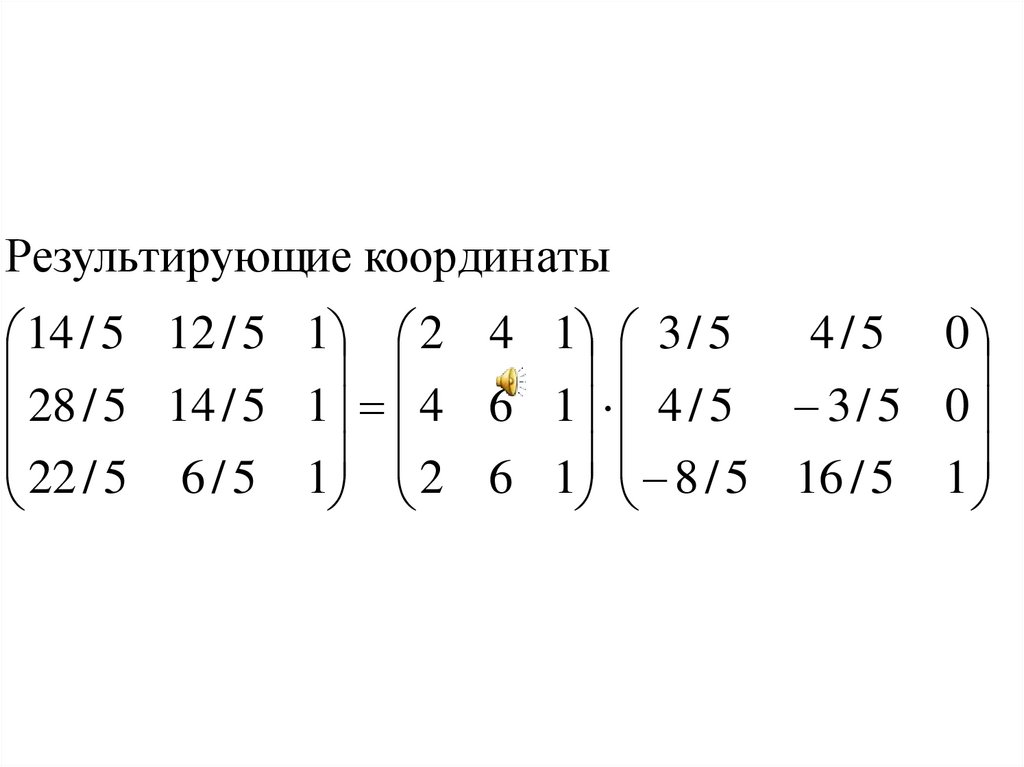
Результирующие координаты4 / 5 0
14 / 5 12 / 5 1 2 4 1 3 / 5
28 / 5 14 / 5 1 4 6 1 4 / 5 3 / 5 0
22 / 5 6 / 5 1 2 6 1 8 / 5 16 / 5 1
9. Пример
y 0.5( x 4)Пример
A 2,4 , B 4,6 , C 2,6
k 0.5
y k x b
k k 1 k 1 / k 2
y 2 x b
4 2 2 b b 8
y 2 x 8
10. Пример
y 0.5 x 4y 2 x 8
0.5 x 4 2 x 8 2.5 x 6 x 12 / 5, y 16 / 5
A 2,4
A 12 / 5,16 / 5
A x , y
12 / 5 0.5 2 x
x 14 / 5, y 12 / 5
16 / 5 0.5 4 y
11. Пример
y 0.5( x 4)Пример
A 2,4 , B 4,6 , C 2,6
k 0.5
y k x b
k k 1 k 1 / k 2
y 2 x b
6 2 4 b b 14
y 2 x 14
12. Пример
y 0.5 x 4y 2 x 14
0.5 x 4 2 x 14 2.5 x 12 x 24 / 5, y 22 / 5
B 4,6
B 24 / 5,22 / 5
B x , y
24 / 5 0.5 4 x
x 28 / 5, y 14 / 5
22 / 5 0.5 6 y
13. Пример
y 0.5( x 4)Пример
A 2,4 , B 4,6 , C 2,6
k 0.5
y k x b
k k 1 k 1 / k 2
y 2 x b
6 2 2 b b 10
y 2 x 10
14. Пример
y 0.5 x 4y 2 x 10
0.5 x 4 2 x 10 2.5 x 8 x 16 / 5, y 18 / 5
С 2,6
С 16 / 5,18 / 5
С x , y
16 / 5 0.5 2 x
x 22 / 5, y 6 / 5
18 / 5 0.5 6 y
15. Ещё пример
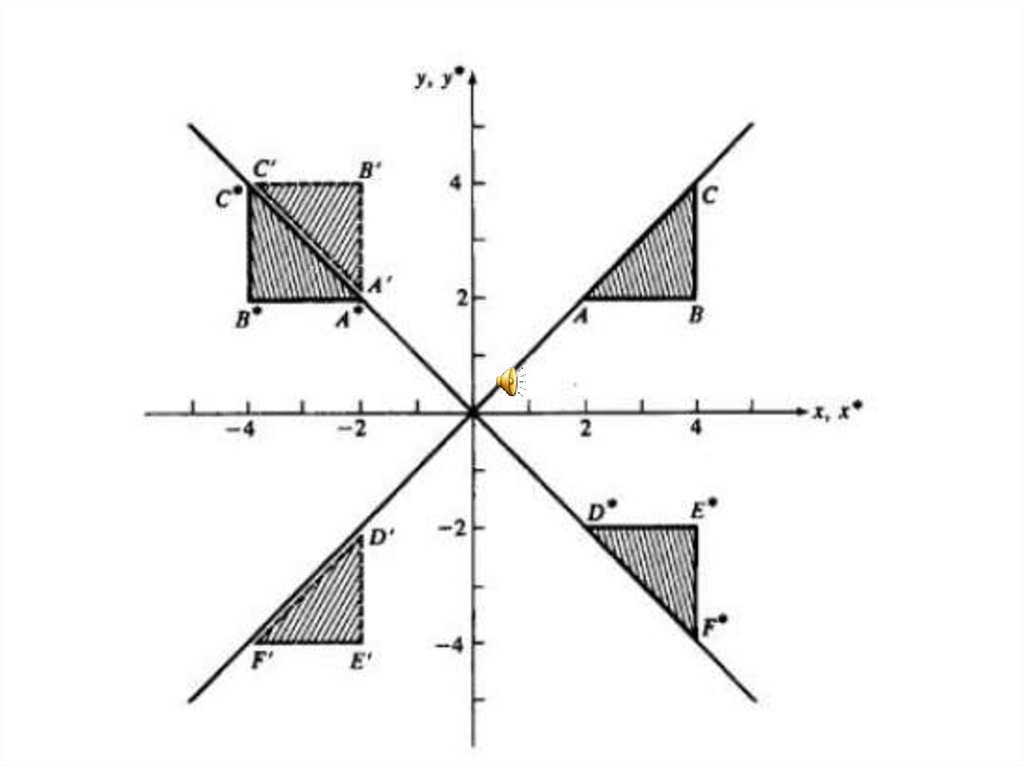
Дан треугольник АВС, А(2,2), В(4,2),С(4,4). Найти координаты треугольника,
полученного из исходного треугольника в
результате следующих преобразований:
1.Поворот на +90 градусов относительно
точки начала координат
2. Отражение относительно линии y=-x
16. Поворот
Старые координаты x r cos , y r sinНовые координаты
x1 r cos , y1 r sin
x1 r cos cos sin sin , y1 r cos sin sin cos
x1 x cos y sin , y1 x sin y cos
cos
Матрица поворотаV
sin
sin
, x1
cos
y1 x
y V
17. Поворот
Старые координаты x r cos , y r sinНовые координаты
x1 r cos , y1 r sin
x1 r cos cos sin sin , y1 r sin cos cos sin
x1 x cos y sin , y1 y cos x sin
cos
Матрица поворотаV
sin
sin
, x1
cos
y1 x
y V
18. Отражение
x 01 0
R
0 1
x1 y1 x y R
x1 x, y1 y
y 0
1 0
R
0 1
x1 y1 x y R
x1 x, y1 y
19. Отражение
y x0 1
R
1 0
x1 y1 x
y R
x1 y, y1 x
y x
0 1
R
1 0
x1 y1 x y R
x1 y, y1 x
20. Результирующая матрица
0 10 1
, R
V
1 0
1 0
1 0
T V R
0 1
1 0
T1 R V
0 1
21.
22. Результирующие координаты
2 2y1 2 2
y2 4 2 T 4 2
y3 4 4
4
4
1 0
T
0 1
x1
x2
x
3
2 2
y1 2 2
y2 4 2 T1 4 2
y3 4 4
4
4
1 0
T1
0 1
x1
x2
x
3
23. Преобразование единичного квадрата
01
1
0
0
0
0
0 a b a
b
1 c d a c b d
1
d
c
a b
ab cd c
b
Ap a c b d
b b d c a c ad bc
c d
2
2 2
2
Ap As ad bc As
a
b
c
d
24.
25. Ещё один пример
ABC , A 1,0 , B 0,1 , C 1,03 2
T
1 2
A B C
1
S ABC 2 1 1, S A B C S ABC ad bc 8
2
2
1 0
3
3 2
1 2
0 1
1 0 1 2 3 2
1
S A B C 4 4 8
2
26.
27. Масштабирование
a bT
c d
a d , b c 0 пропорциональное
a d 1 растяжение
a d 1 сжатие
a d , b c 0 непропорциональное
28.
29. Матрицы преобразований
2 0T1
0 2
1 / 2 0
T2
0 3
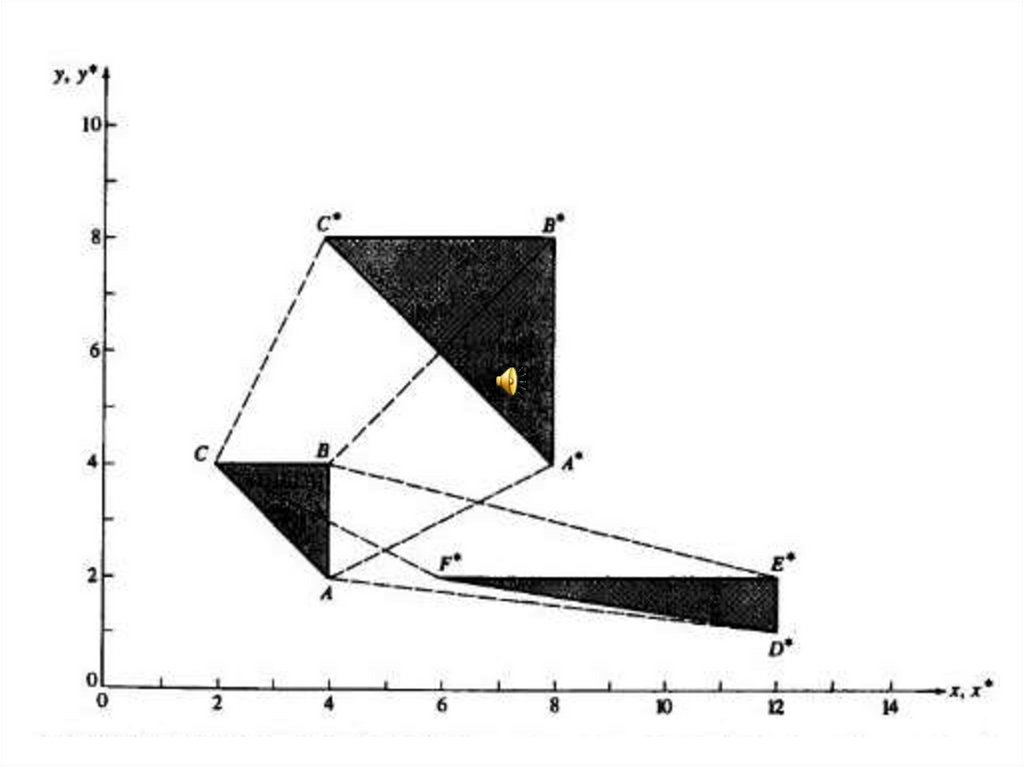
ABC , A 4,2 , B 4,4 , C 2,4
4 2
8 4
2 0
4 4
8 8
0 2
2
4
4
8
4 2
2 6
1 / 2 0
4 4
2 12
0 3
2
4
1
12
30.
31.
2 0T1
0 2
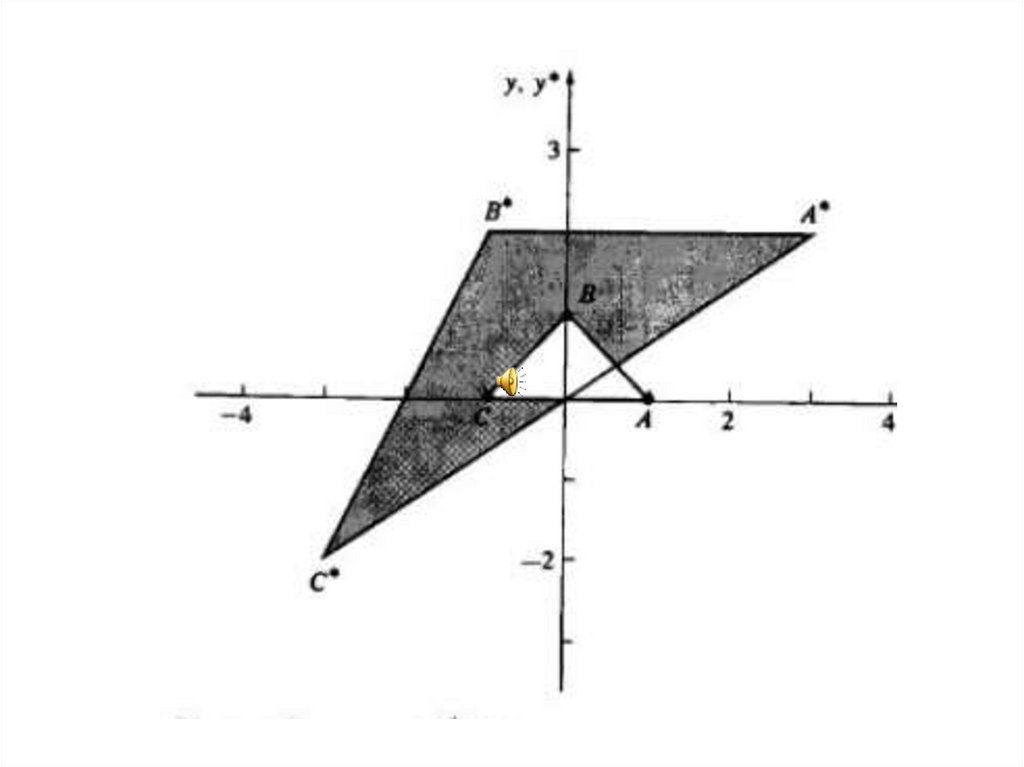
ABC , A 1, 1 , B 2, 1 , C 1,2
1 1
2 2
2 0
2 1
4 2
0 2
1
2
2
4

























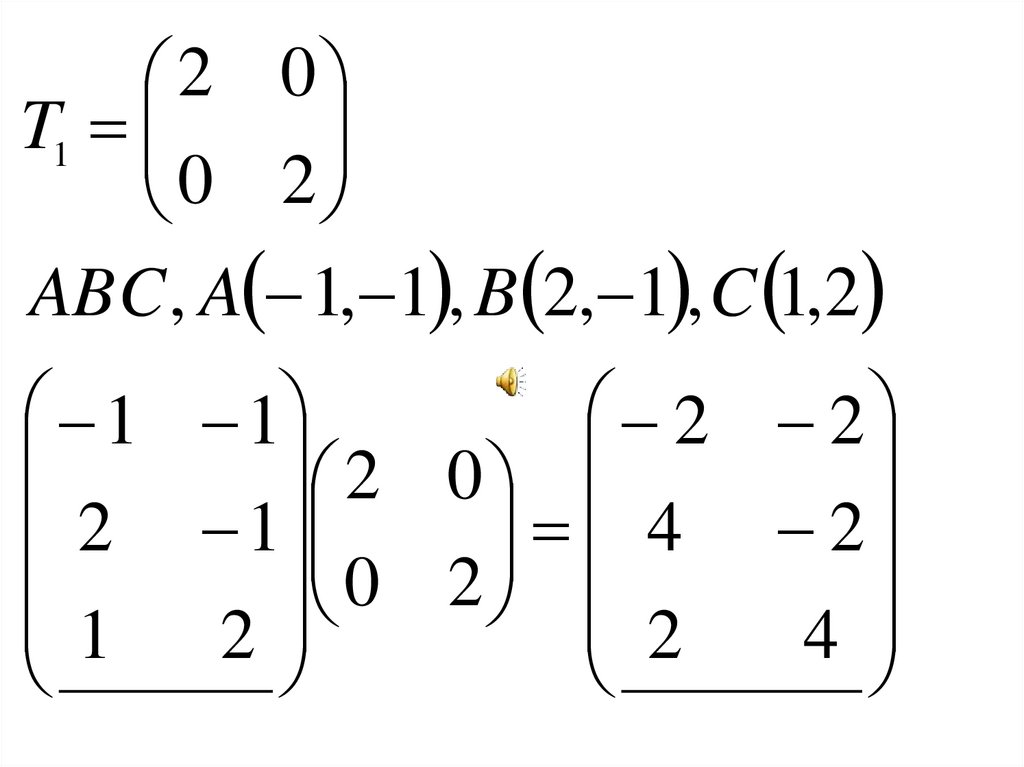
 mathematics
mathematics