Функция. Область определения и область значений функции

1.

Функция.
Область определения и
область значений функции.

2. Функция – это зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное

значение переменной у.
х – независимая переменная или
аргумент
у – зависимая переменная
значение функции
или

3.

Если зависимость переменной у от
переменной х является функцией, то коротко
это записывают так:
у = f(х)
Пример.
у = 2х + 3
или
Если х = 5, то f(5)
f(х) = 2х + 3
= 2 5 + 3=10 + 3 = 13
Если f(х) = 0, то 2х + 3 = 0
2х = -3
х = -1,5

4.

Область определения функции – все значения
независимой переменной х.
Обозначение: D(
f)
Область значений функции – все значения
зависимой переменной у.
Обозначение: Е(
f)
Если функция у = f(х) задана формулой и ее
область определения не указана, то считают,
что область определения функции состоит из
всех значений х, при которых выражение f(х)
имеет смысл.

5.

Пример. Найти область определения
функции:
f(х) = 2х + 3
D(f)=R или D(f) = (- ; + )
x
2) f(х) = х +
3
5x + 2
3) f(х) =
x-8
х – 8 0
х 8
D(f)=R или D(f) = (- ; + )
1)
2
D(f)= (- ; 8) (8; + )
8

6.

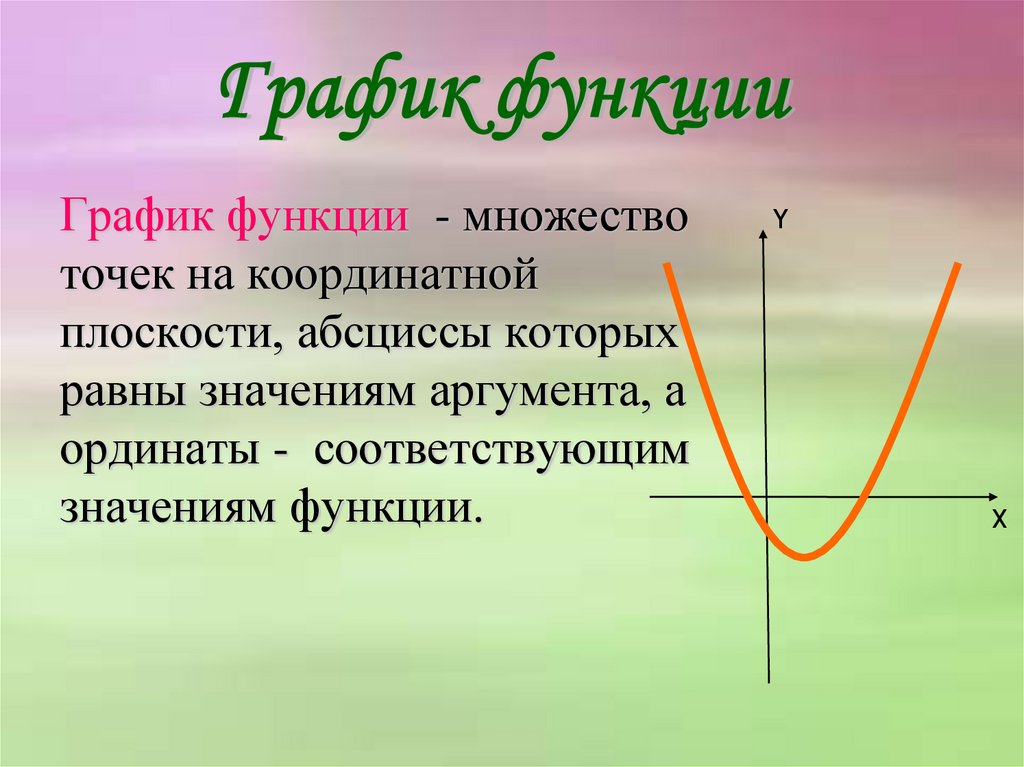
График функции - множество
точек на координатной
плоскости, абсциссы которых
равны значениям аргумента, а
ординаты - соответствующим
значениям функции.
Y
X

7.

Существует несколько основных
видов функций:
линейная функция;
прямая пропорциональность;
обратная пропорциональность;
квадратичная функция;
кубическая функция;
функция корня;
функция модуля.
y
x

8.

функция вида y = k х + b
1. D( f ) = R;
2. E( f ) = R;
3. графиком функции
является прямая
y
k>0
k=0
x
k<0

9.

функция вида y = k х
1. D( f ) = R;
2. E( f ) = R;
3. графиком функции
является прямая,
проходящая через
начало координат.
y
x

10.

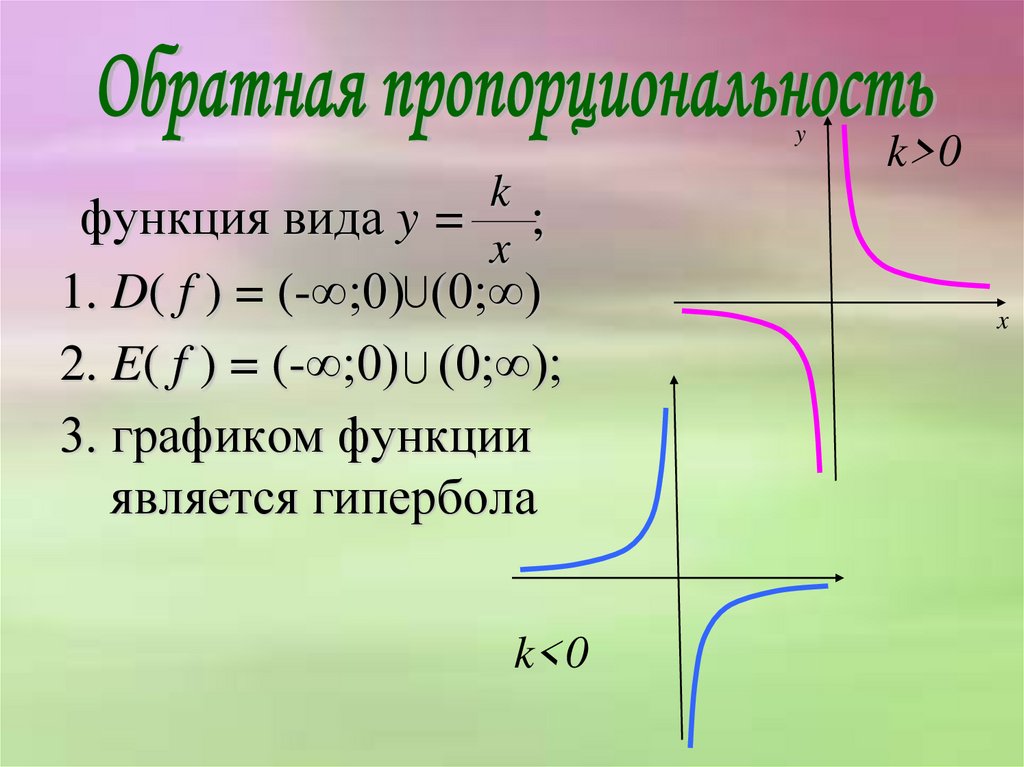
y
k
функция вида y = ;
x
1. D( f ) = (-∞;0) (0;∞)
2. E( f ) = (-∞;0) (0;∞);
3. графиком функции
является гипербола
k<0
k>0
x

11.

функция вида y = x² ;
1.D( f ) = R;
2. E( f ) = [0;∞);
3. графиком функции
является парабола
y
x

12.

функция вида y = x³;
1. D( f ) = R;
2. E( f ) = R;
3. графиком функции
является кубическая
парабола.
y
x

13.

функция вида y = x ;
1. D( f ) = [0;∞);
2. E( f ) = [0;∞);
3. графиком функции
является ветвь
параболы.
y
x

14.

функция вида y = |x|;
1. D( f ) = R;
2. E( f ) = [0;∞);
3. график функции на
промежутке [0;∞)
совпадает с графиком
функции у = х, а на
промежутке (-∞;0] – с
графиком функции у = -х
y
x

15. 1. Каждый график соотнесите с соответствующей ему формулой:

k
y=
x
y = 2x
y
y
x
y = x²
y = 2x + 2
y
y
x
x
x

16. 2. Каждую прямую соотнесите с её уравнением:

y x
y 2
x 2
y
y
x
y 2
y
y
x
x
x