Определение функции

1.

2. Функция – это зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное

значение переменной у.
х – независимая переменная или
аргумент
у – зависимая переменная
значение функции
или

3.

Область определения функции – все значения
независимой переменной х.
Обозначение: D( f )
Область значений функции – все значения
зависимой переменной у.
Обозначение: Е( f )
Если функция у = f(х) задана формулой и ее
область определения не указана, то считают,
что область определения функции состоит из
всех значений х, при которых выражение f(х)
имеет смысл.

4.

Пример. Найти область определения
функции:
1) f(х) = 2х + 3
D(f)=R или D(f) = (- ; + )
x
2) f(х) = х +
3
5x + 2
3) f(х) =
x-8
х – 8 0
х 8
D(f)=R или D(f) = (- ; + )
2
D(f)= (- ; 8) (8; + )
8

5.

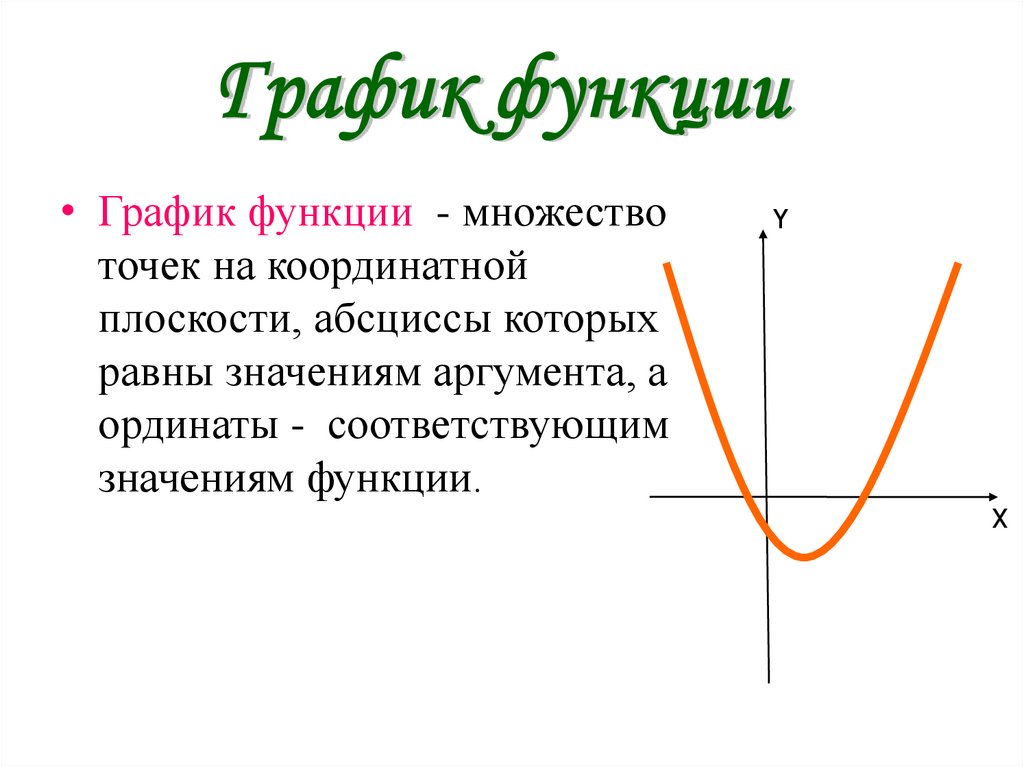
• График функции - множество
точек на координатной
плоскости, абсциссы которых
равны значениям аргумента, а
ординаты - соответствующим
значениям функции.
Y
X

6.

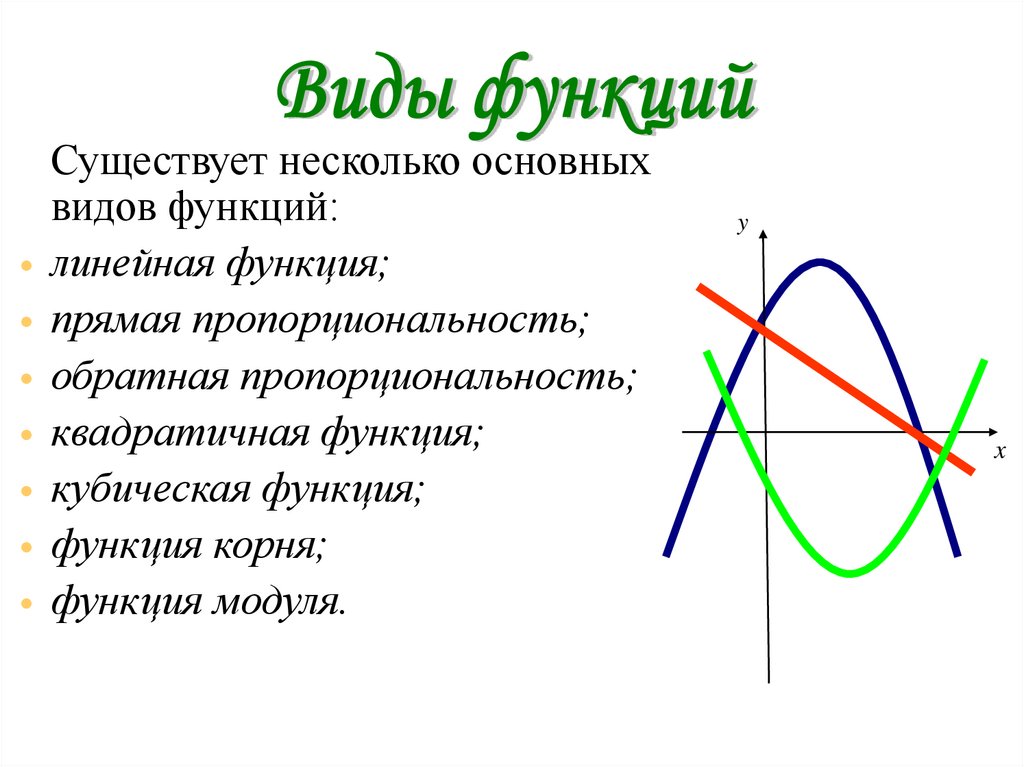
Существует несколько основных
видов функций:
• линейная функция;
• прямая пропорциональность;
• обратная пропорциональность;
• квадратичная функция;
• кубическая функция;
• функция корня;
• функция модуля.
y
x

7.

функция вида y = k х + b
• 1. D( f ) = R;
2. E( f ) = R;
3. графиком функции
является прямая
y
k>0
k=0
x
k<0

8.

функция вида y = k х
• 1. D( f ) = R;
2. E( f ) = R;
3. графиком функции
является прямая,
проходящая через
начало координат.
y
x

9.

y
k
• функция вида у= x
• 1. D(f)=(-∞;0) (0;∞)
• 2. E(f)=(-∞;0) (0;∞);
• 3. графиком функции
является гипербола
k<0
k>0
x

10.

• функция вида y = x² ;
• 1. D( f ) = R;
• 2. E( f ) = [0;∞);
• 3. графиком функции
является парабола
y
x

11.

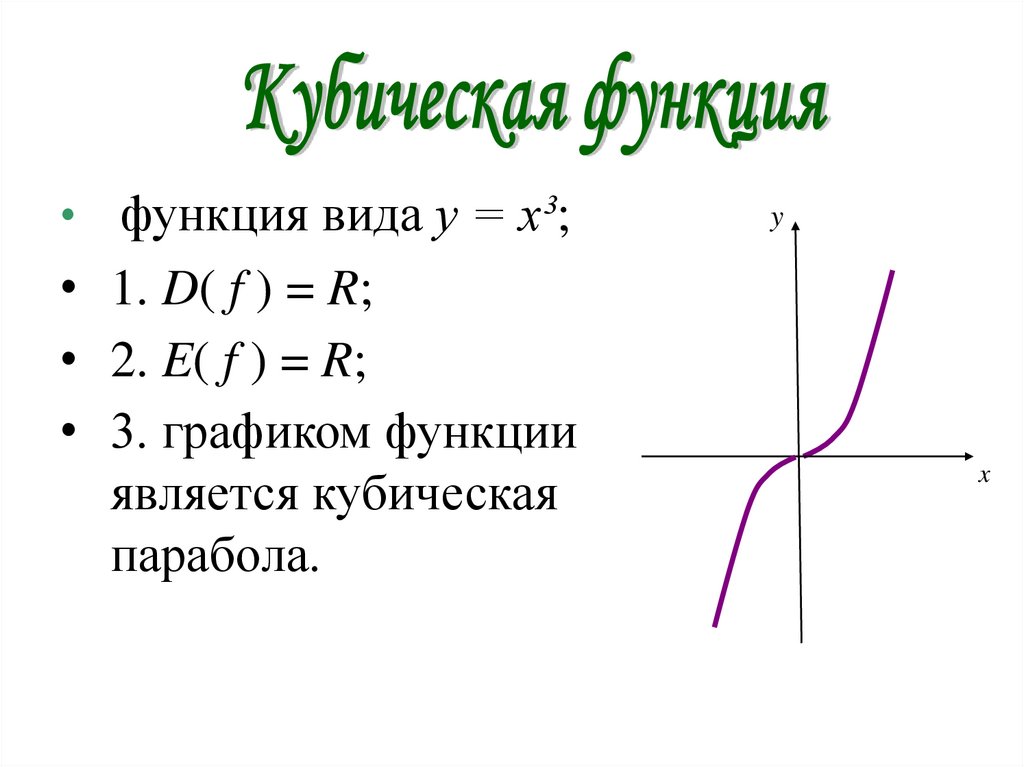
• функция вида y = x³;
• 1. D( f ) = R;
• 2. E( f ) = R;
• 3. графиком функции
является кубическая
парабола.
y
x

12.

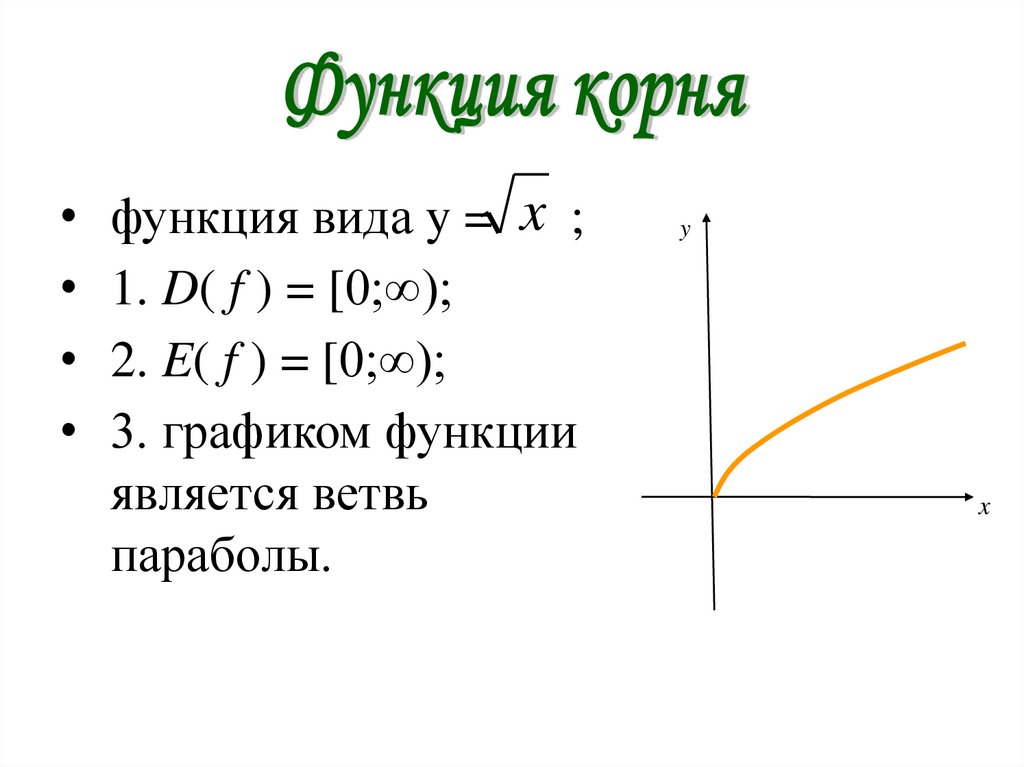
• функция вида y = x ;
• 1. D( f ) = [0;∞);
• 2. E( f ) = [0;∞);
• 3. графиком функции
является ветвь
параболы.
y
x

13. Функция модуля

• функция вида y = |x|
• 1. D( f ) = R;
• 2. E( f ) = [0;∞);
y
0
x

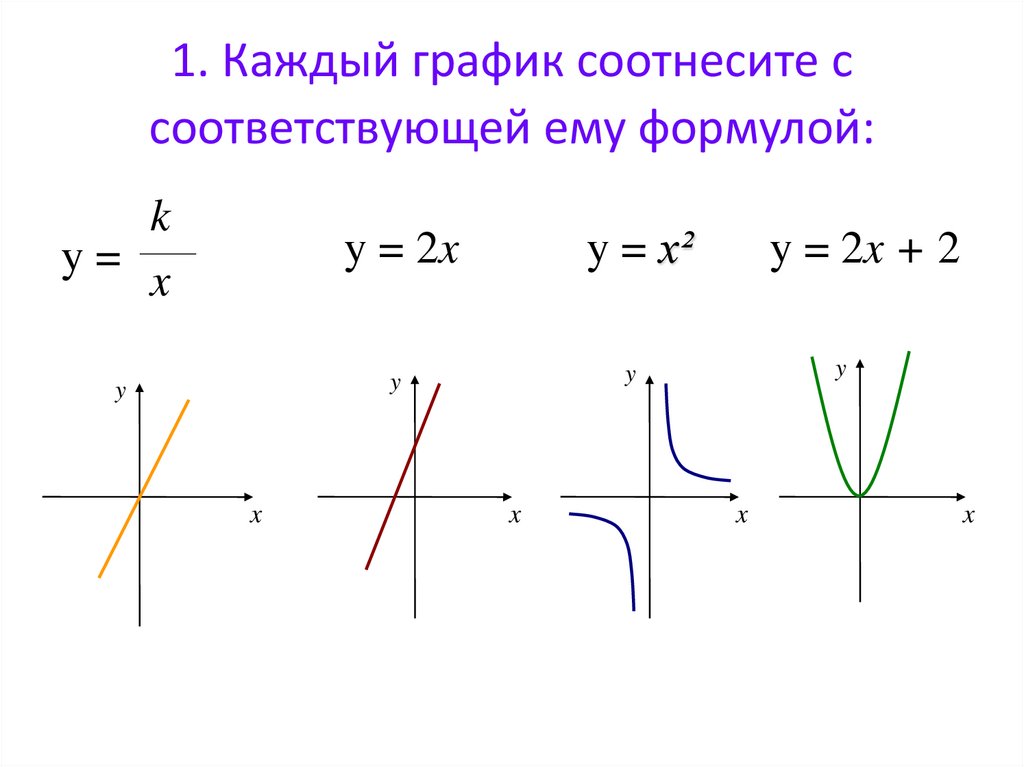
14. 1. Каждый график соотнесите с соответствующей ему формулой:

k
y=
x
y = 2x
y = x²
y
y
y
x
x
y = 2x + 2
y
x
x

15. 2. Каждую прямую соотнесите с её уравнением:

y x
x 2
y 2
y 2
y
y
y
y
x
x
x
x

16. 3 а: Прочитайте графики функций

y
y
4
-2
0
x
x
0
-2
y = |x| + 4
y = |x+2| - 2

17. 3б: Прочитайте графики функций

y
y
1
x
1
0
y = |x -1|
x
0
-3
y = -|x| -3

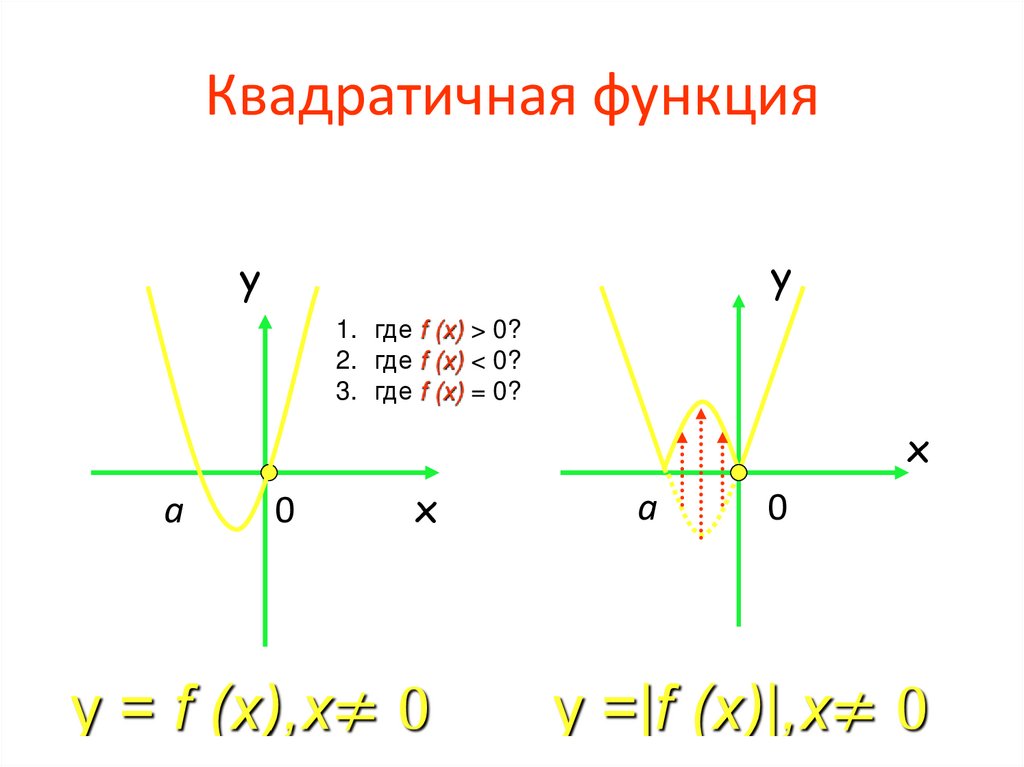
18. Квадратичная функция

y
y
1. где f (x) > 0?
2. где f (x) < 0?
3. где f (x) = 0?
x
a
0
x
a
0

19. Тема урока: Свойства и графики элементарных функций.

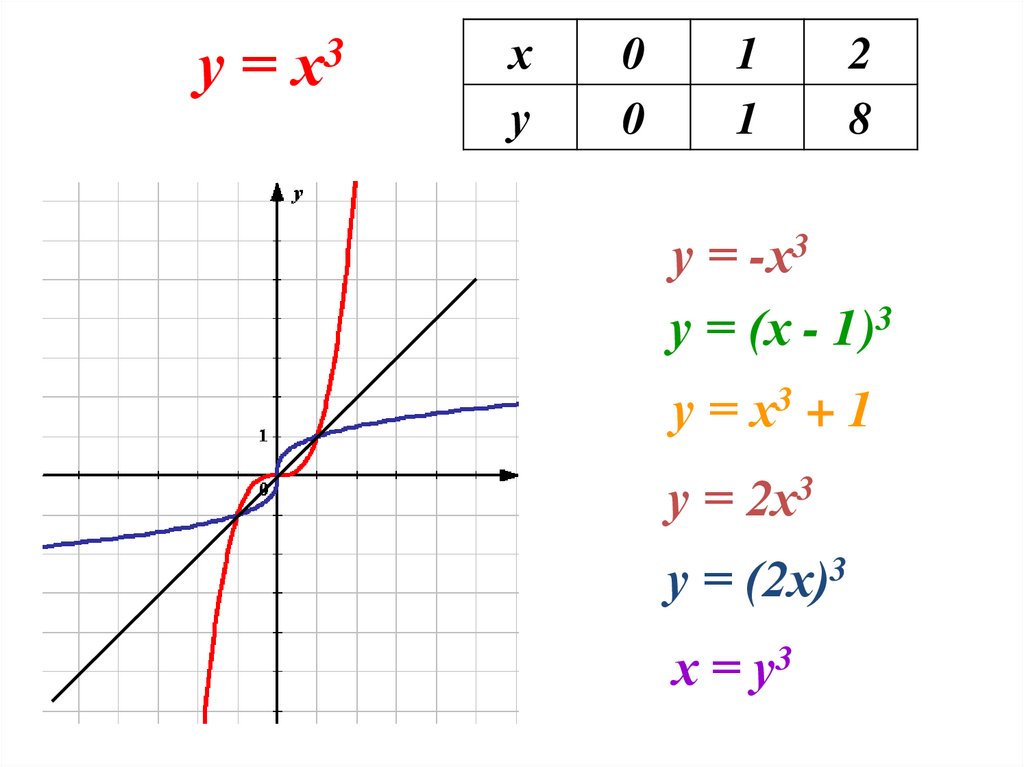
20. у = х3

3
у=х
х
у
0
0
1
1
2
8
у = -х3
у = (х - 1)3
у = х3 + 1
у = 2х3
у = (2х)3
х = у3

21.

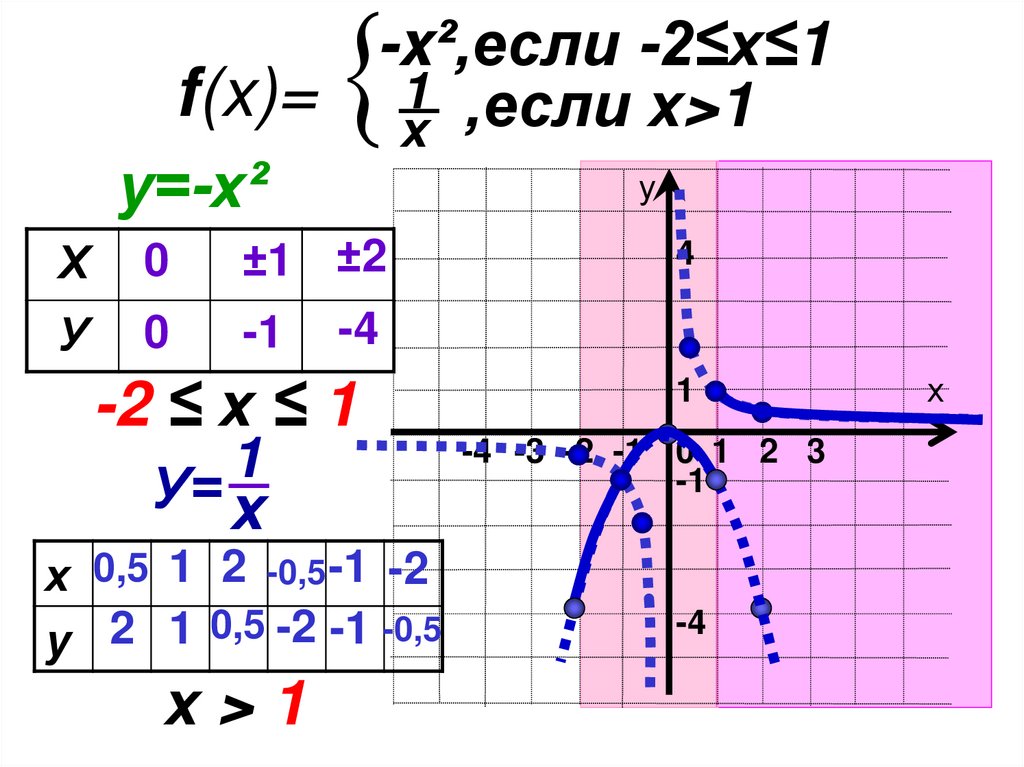
Постройте график функции
-x²,если -2≤х≤1
f(x)= 1х ,если х>1
и опишите её свойства.

22.

-x²,если -2≤х≤1
f(x)= 1х ,если х>1
у
у=-х²
Х
0
У
0
±1 ±2
-1 -4
-2 ≤ х ≤ 1
1
У= х
х 0,5 1 2 -0,5 -1 -2
у 2 1 0,5 -2 -1 -0,5
х>1
4
1
-4 -3 -2 -1 0 1 2 3
-1
-4
х

23.

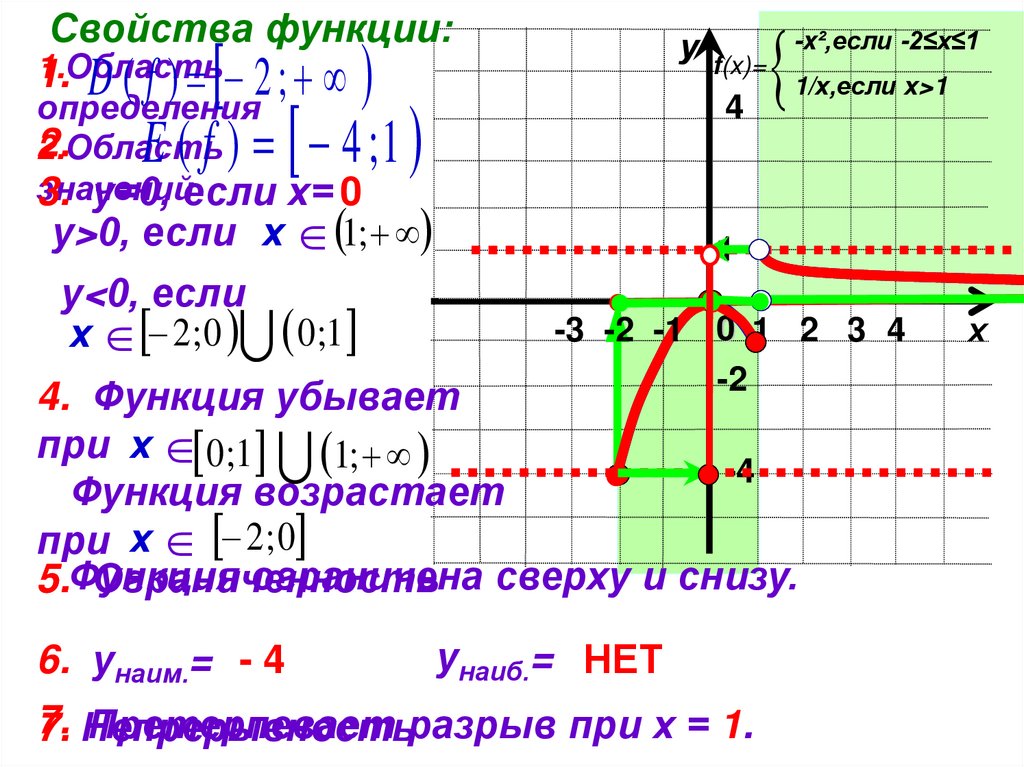
Свойства функции:
1.Область
1. D ( f ) 2 ;
определения
у f(x)=
E ( f ) 4 ;1
4
-x²,если -2≤х≤1
1/х,если х>1
2.
2.Область
значений
3. у=0, если х= 0
у>0, если х 1;
у<0, если
х 2; 0 0;1
1
-3 -2 -1 0 1 2 3 4
-2
4. Функция убывает
при х 0 ;1 1;
-4
Функция возрастает
при х 2 ; 0
ограничена сверху и снизу.
5.Функция
Ограниченность
6. унаим.= - 4
унаиб.= НЕТ
7. Непрерывность
Претерпевает разрыв при х = 1.
х

24.

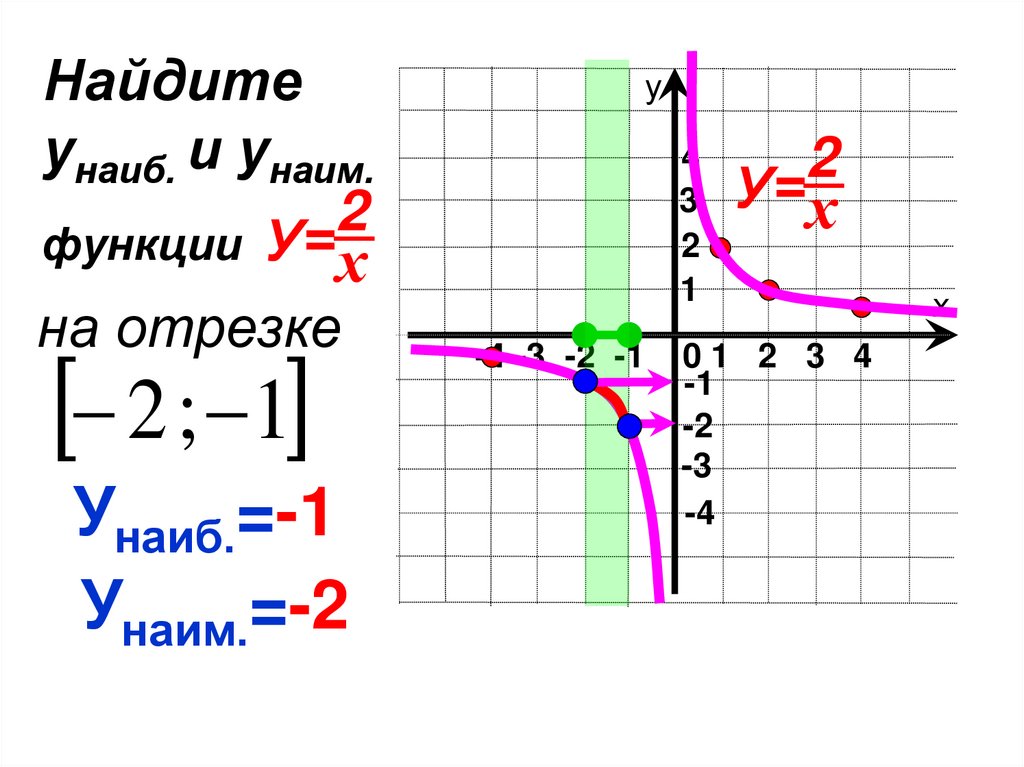
Найдите
унаиб. и унаим.
2
функции У=х
на отрезке
2 ; 1
Унаиб.=-1
Унаим.=-2
у
4
3
2
1
-4 -3 -2 -1
2
У=х
01 2 3 4
-1
-2
-3
-4
х

25.

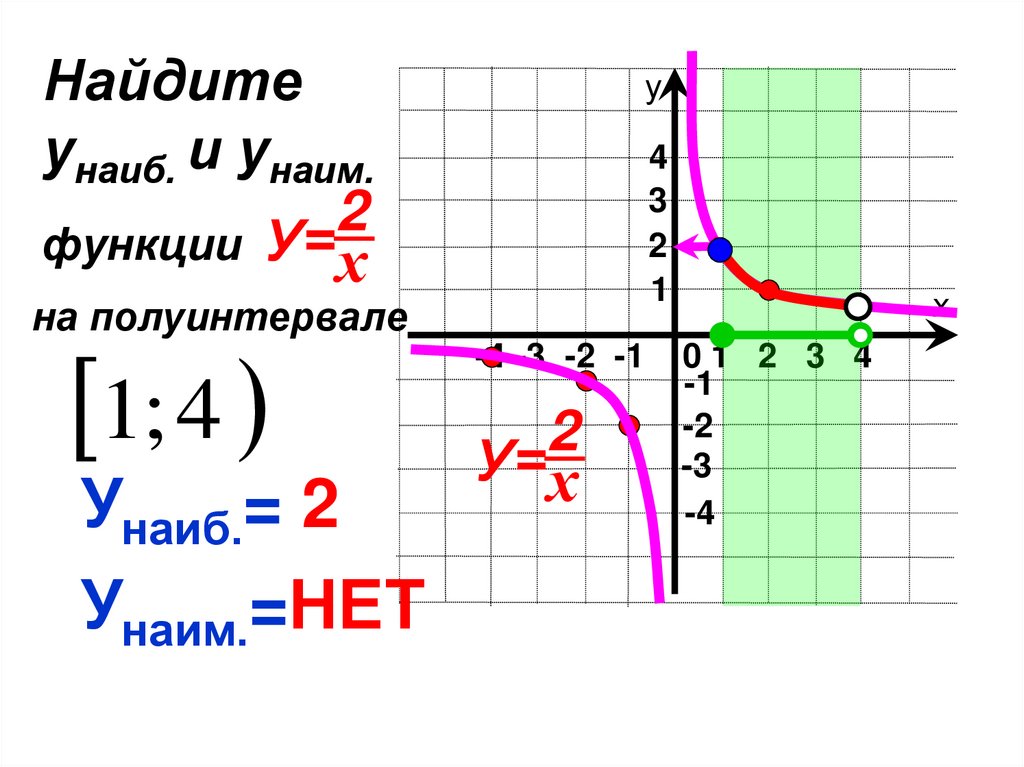
Найдите
унаиб. и унаим.
2
функции У=х
у
4
3
2
1
на полуинтервале
1; 4
Унаиб.= 2
Унаим.=НЕТ
-4 -3 -2 -1
2
У=х
х
01 2 3 4
-1
-2
-3
-4

26.

Д/з: 1. Постройте график
функции
√x+3,если -3≤х≤1
f(x)= 2(х-1)²,если 1<х≤2
и опишите её свойства.

27.

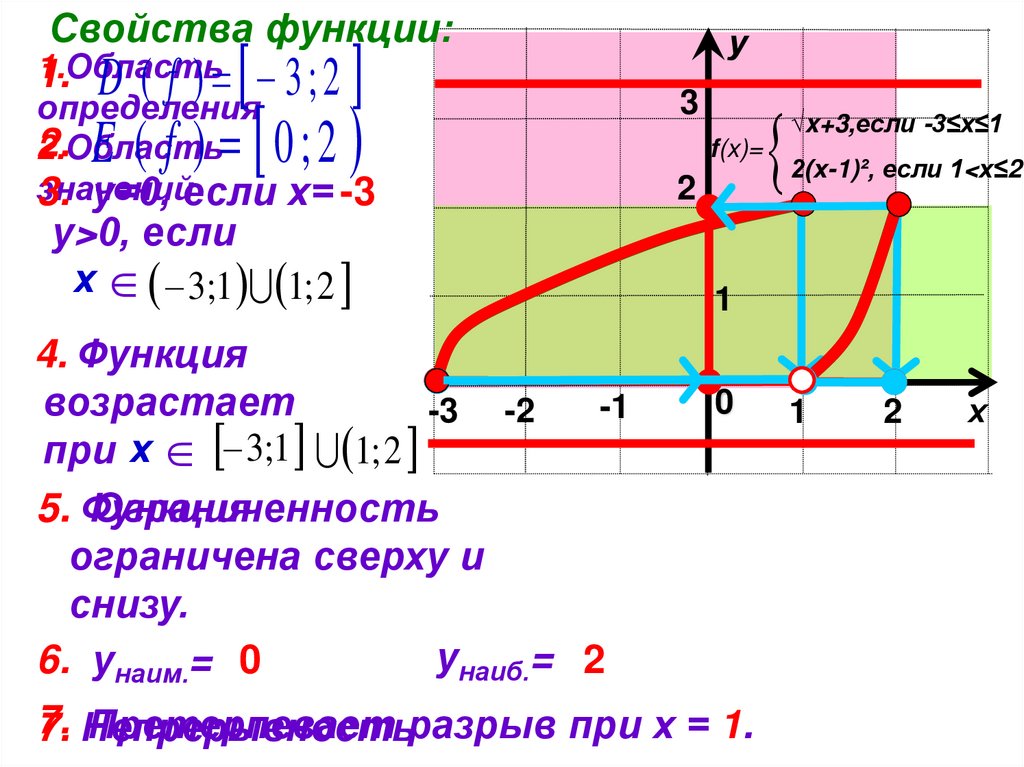
Свойства функции:
1.Область
1. D ( f ) 3 ; 2
определения
у
E ( f ) 0;2
3
2.
2.Область
значений
3. у=0, если х= -3
f(x)=
2
у>0, если
х 3;1 1; 2
4. Функция
возрастает
-3
при х 3;1 1; 2
√x+3,если -3≤х≤1
2(х-1)², если 1<х≤2
1
-2
-1
0
5. Функция
Ограниченность
ограничена сверху и
снизу.
унаиб.= 2
6. унаим.= 0
7. Непрерывность
Претерпевает разрыв при х = 1.
1
2
х