Определитель матрицы третьего порядка (Занятие 3)

1. Определитель матрицы третьего порядка

2.

Пусть матрица А имеет размерность 3 3:
а11
А а 21
а
31
а12
а 22
а32
а13
а 23
а33
Определителем 3-го порядка называется число
а11 а12 а13
det( A) а 21 а 22 а 23 a11 a 22 a33 a13 a 21 a32 a12 a 23 a31 a13 a 22 a31 a12 a 21 a33 a11 a 23 a32
а31 а32 а33
Примеры
1.
1 1 4
2 0 3 1 0 1 4 2 5 1 3 0 4 0 0 1 2 1 1 3 5 23
0 5 1
2..
5
1 3
4
3
2 ?
4
2
5

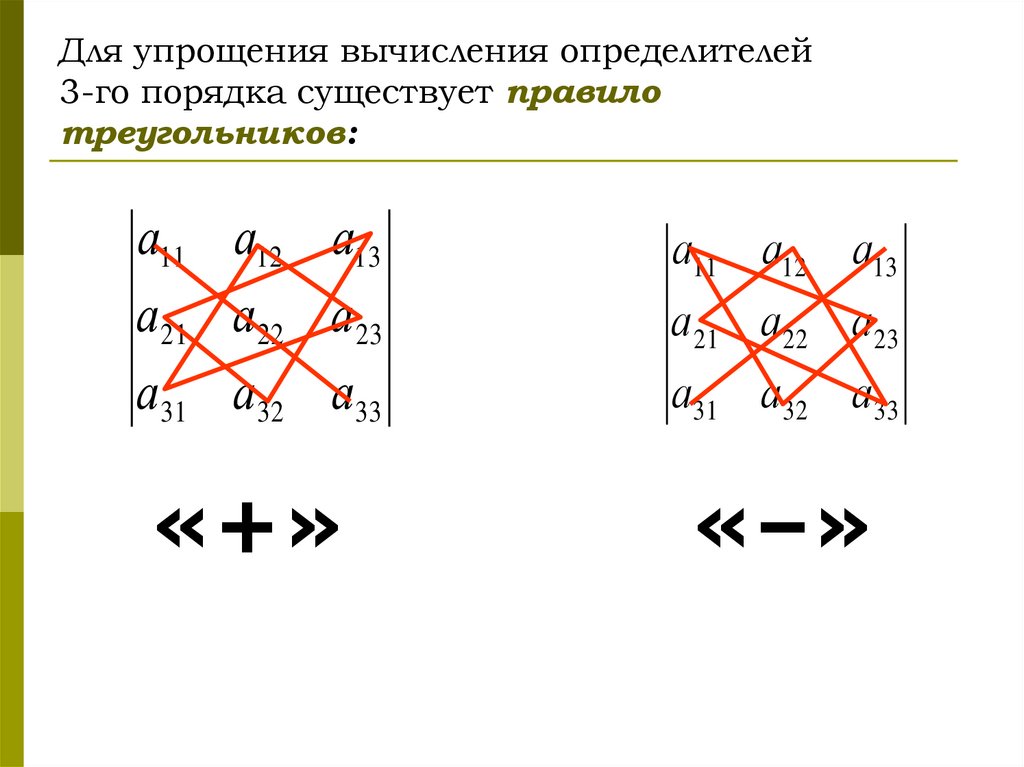
3. Для упрощения вычисления определителей 3-го порядка существует правило треугольников:

а11 а12 а13
а11 а12 а13
а 21 а 22 а 23
а 21 а 22 а 23
а31 а32 а33
а31 а32 а33
«+»
«–»

4. Правило Саррюса (параллельных)

Справа от определителя дописывают первых 2 столбца
(или внизу 2 строки) и произведения элементов на
главной диагонали и на диагоналях, ей параллельных,
берут со знаком "плюс"; а произведения элементов
побочной диагонали и диагоналей, ей параллельных, со
знаком "минус":

5. Пример

6. Задание

Выпишите определение определтеля 3
порядка
Зарисуйте схематично правила
треугольников и параллельных
Выполните пример 2 методами
треугольников и параллельных.