Similar presentations:
Модели колебаний (лекция 7)
1.
Лекция 7МОДЕЛИ
КОЛЕБАНИЙ
Вопросы:
1. Свободные затухающие колебания.
Характеристики затухания.
2. Вынужденные колебания. Резонанс.
2.
Затухающими являются колебания, происходящие вдиссипативной колебательной системе. В реальной
колебательной системе имеются силы сопротивления
(трения), действие которых уменьшает энергию
колебаний.
При небольших скоростях движения в среде
сила сопротивления пропорциональна скорости:
Fсопр x
dx
r vx r
dt
где r коэффициент сопротивления среды, [r]
= кг/с.
Знак минус в формуле показывает, что сила и скорость
имеют противоположные направления.
3.
Уравнение движения (второй закон Ньютона) приналичии квазиупругих сил и сил сопротивления имеет
вид:
max kx r v x
Обозначения:
β
r
2 ;
m
k
m
2
0
– коэффициент затухания колебаний;
ω0
[β] = 1/с
– собственная циклическая частота колебаний
системы (частота, с которой происходили бы свободные
колебания системы при отсутствии сопротивления среды,
т.е. при r = 0).
4.
Дифференциальное уравнение свободных затухающихколебаний примет вид:
2
d x
dx
2
2β
ω0 x 0
2
dt
dt
Общее решение этого уравнения имеет вид:
x A0e
з
2
0
2
t
cos( зt )
циклическая частота затухающих
колебаний.
А0 и фаза определяются
х(0) = х0; υ(0) = υ0.
Начальные амплитуда
начальных условий:
из
5.
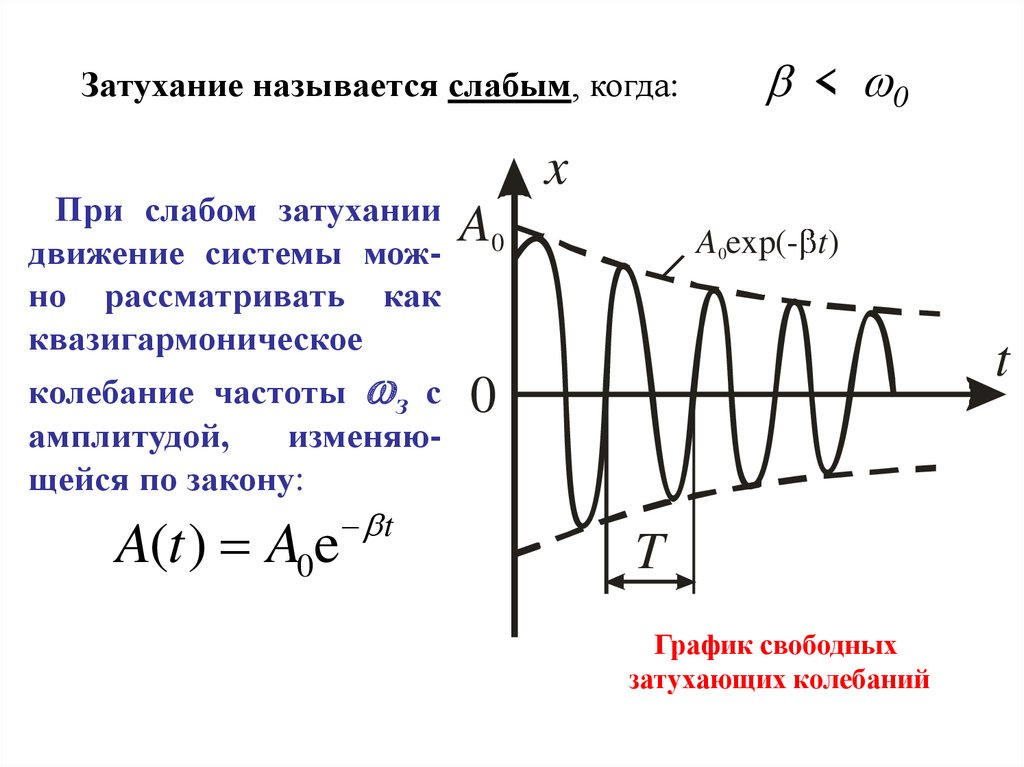
Затухание называется слабым, когда:При слабом затухании
движение системы можно рассматривать как
квазигармоническое
колебание частоты з с
амплитудой,
изменяющейся по закону:
t
A(t ) A0e
< 0
x
A0
A0exp(- t)
t
0
T
График свободных
затухающих колебаний
6.
Характеристики затухания1. Коэффициент затухания колебаний
скорость затухания колебаний:
r
2. Время релаксации
характеризует
2m
– время, за которое амплитуда
колебаний уменьшается в е ≈ 2,7 раз:
t
A0e
A(t )
e
e
( t )
A(t ) A0e
откуда
= 1, или:
1
Физический смысл коэффициента затухания колебаний:
это величина, обратно пропорциональная времени,
за которое амплитуда колебаний уменьшается в е раз.
7.
3. Период затухающих колебаний:T
2
з
2
2
0
2
4. Декремент затухания – отношение значений амплитуд,
соответствующих моментам времени, отличающимся на
период:
T
A(t )
e
A(t T )
5. Логарифмический декремент затухания θ –
натуральный логарифм от декремента затухания:
A(t )
θ ln
T
A(t T )
8.
За время система успевает совершитьчисло колебаний, равное:
Физический
смысл
логарифмического
декремента затухания − это величина,
обратная числу колебаний, совершаемых за
время релаксации (за время уменьшения
амплитуды в е раз):
Ne
T
1
θ
Ne
6. Добротность Q системы – безразмерная величина, обратно пропорциональная потерям энергии в колебательной
системе.
Q 2
=
π/θ N e
Запас энергии в колебательной системе
Потери энергии за один период колебаний
Для идеальной системы (без затухания колебаний): Q
→∞
9.
Вынужденные колебанияВынужденными называются такие колебания, которые
возникают в колебательной системе под действием
внешней периодически изменяющейся силы (вынуждающей силы). Вынужденные колебания – это
незатухающие колебания.
Вынуждающая сила изменяется
со временем по гармоническому
закону:
x
Fx F0 cos t
t
период
установивш иеся
установления
колебания
колебаний
ω
– частота вынуждающей
силы;
F0
– амплитуда вынуждающей
силы.
10.
В уравнении движения (втором законе Ньютона) кромеквазиупругой силы и силы сопротивления среды
учитываем вынуждающую силу:
max kx r v x F0 cos t
Дифференциальное уравнение вынужденных колебаний:
2
F0
d x
dx
2
2β
ω0 x
cos t
2
dt
dt
m
Это неоднородное (правая часть отлична от нуля)
дифференциальное уравнение второго порядка с
постоянными коэффициентами.
11.
Общее решение неоднородного уравненияравно сумме общего решения соответствующего однородного уравнения, и частного
решения данного неоднородного уравнения:
x A0e
t
cos( зt ) A cos( t )
Жан
Даламбер
(1717 – 1783)
Первое слагаемое играет роль только при установлении
колебаний. С течением времени из-за множителя e t роль
этого слагаемого уменьшается. После установления
колебаний первым слагаемым можно пренебречь, сохраняя
лишь второе, которое описывает установившиеся
вынужденные гармонические колебания с частотой,
равной частоте вынуждающей силы:
x A cos( t )
12.
Амплитуда вынужденных колебаний зависит от частотывынуждающей силы.
Вынужденные колебания отстают по фазе от
вынуждающей силы, причем величина отставания
также зависит от частоты вынуждающей силы.
A
F0 / m
( ) 4
2
0
2 2
2
;
2
2
tg 2
2
0
Явление резкого возрастания амплитуды вынужденных
колебаний при приближении частоты вынуждающей
силы к некоторому значению, называется резонансом, а
соответствующая частота – резонансной частотой рез.
13.
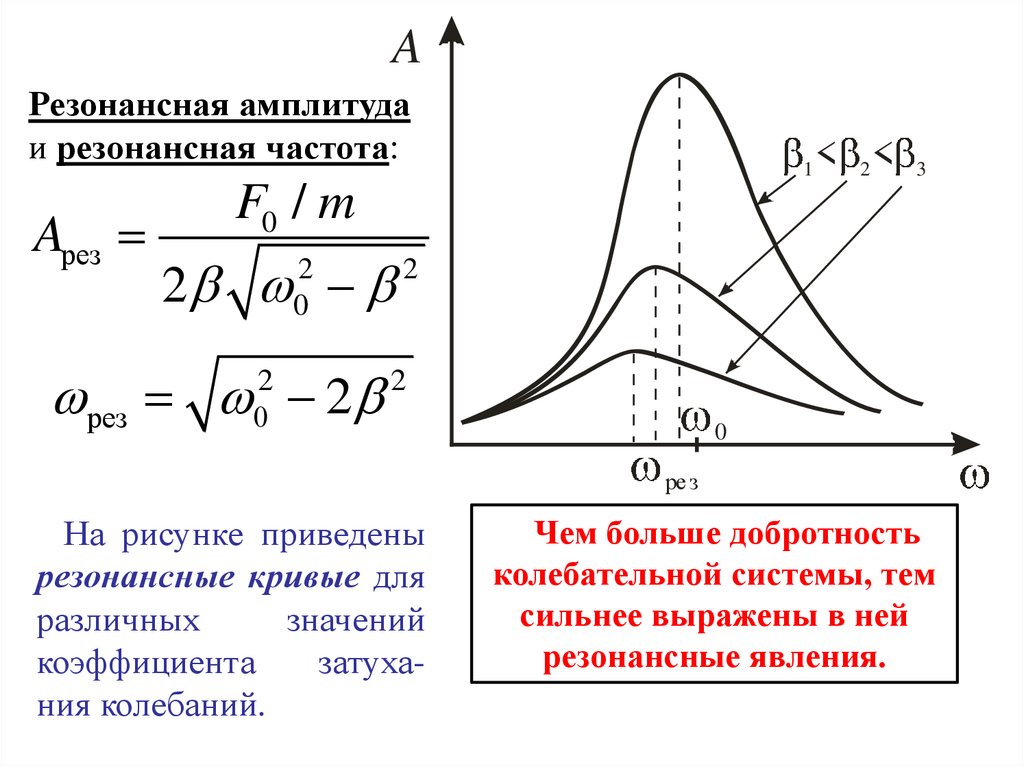
AРезонансная амплитуда
и резонансная частота:
Aрез
1
< 2<
3
F0 / m
2
2
0
рез 2
2
0
2
2
0
рез
На рисунке приведены
резонансные кривые для
различных
значений
коэффициента
затухания колебаний.
Чем больше добротность
колебательной системы, тем
сильнее выражены в ней
резонансные явления.
14.
Необходимость учитывать явление резонанса в технике:при конструировании и эксплуатации машин (станков, самолетов и др.) и различных сооружений (мостов, зданий и
др.) их собственная частота колебаний не должна быть
близкой к частоте возможных внешних воздействий.
Пример: обрушение Египетского
моста в Санкт-Петербурге в 1905
году при прохождении по нему эскадрона гвардейской кавалерии.
Египетский мост сегодня
(восстановлен в другом виде
в 1955 году).












 physics
physics