Similar presentations:
«Способы решения квадратных уравнений». Исследовательская работа
1.
МОУ «СОШ им. Г.И. Марчука р. п. Духовницкое»ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
«СПОСОБЫ РЕШЕНИЯ
КВАДРАТНЫХ УРАВНЕНИЙ»
Авторы:
Балдина Анна Александровна, ученица 10
класса
Фадеева Дарья Александровна, ученица 10
класса
Руководитель:
Кузьмичева Татьяна Владимировна,
учитель математики
р. п. Духовницкое
2020
2.
СодержаниеВведение
1. Опрос учащихся 8-9 классов и его результаты
2. Из истории квадратных уравнений
2.1. Квадратные уравнения в Древнем Вавилоне
2.2. Квадратные уравнения в Индии
2.3. Квадратные уравнения в Европе XII-XVII в
3. Способы решения квадратных уравнений
3.1. Стандартные
3.2. Нестандартные
4. Заключение
5. Список интернет-ресурсов
6.Приложение
3.
К изучению темы«Квадратные
трехчлены» учащиеся
приступают, уже
накопив
определенный опыт,
владея достаточно
большим запасом
алгебраических и
общематематических
представлений,
понятий, умений.
4.
Проблемныйвопрос:
- Существуют ли кроме общепринятых
приемов решения квадратных уравнений
другие, которые позволяют быстро и
рационально решать квадратные
уравнения?
Гипотеза:
- Используя малоизестные приёмы
некоторые виды квадратных уравнений
можно решать достаточно легко.
5.
Цель:- Изучить стандартные и
нестандартные способы решения
квадратных уравнений.
Объект
исследования:
- Квадратные уравнения
Предмет
исследования:
- Стандартные и нестандартные
методы решения квадратных
уравнений
6.
Задачи:- Изучить историю развития теории и
практики решения квадратных
уравнений;
- Изучить стандартные и нестандартные
способы решения квадратных
уравнений;
- Научиться применять нестандартные
способы решения уравнений с большими
коэффициентами;
- Подобрать тренировочные упражнения
для отработки изученных приёмов.
7.
1. ОПРОС1) Умеете ли вы решать квадратные уравнения? Да или
Нет
2) Какими способами решения квадратных уравнений
вы владеете?
А. По теореме Виета
Б. по формуле через D
В. по формуле через D1
Г. другие...
3) Какие сложности вы испытываете при решении
квадратных уравнений?
А. не знаю формул
Б. сложно вычислять
В. путаю коэффициенты
Г. допускаю вычислительные ошибки
Д. не испытываю затруднений
4) Знакомы ли вам какие-либо другие пути решения
квадратных уравнений? Да или Нет
8.
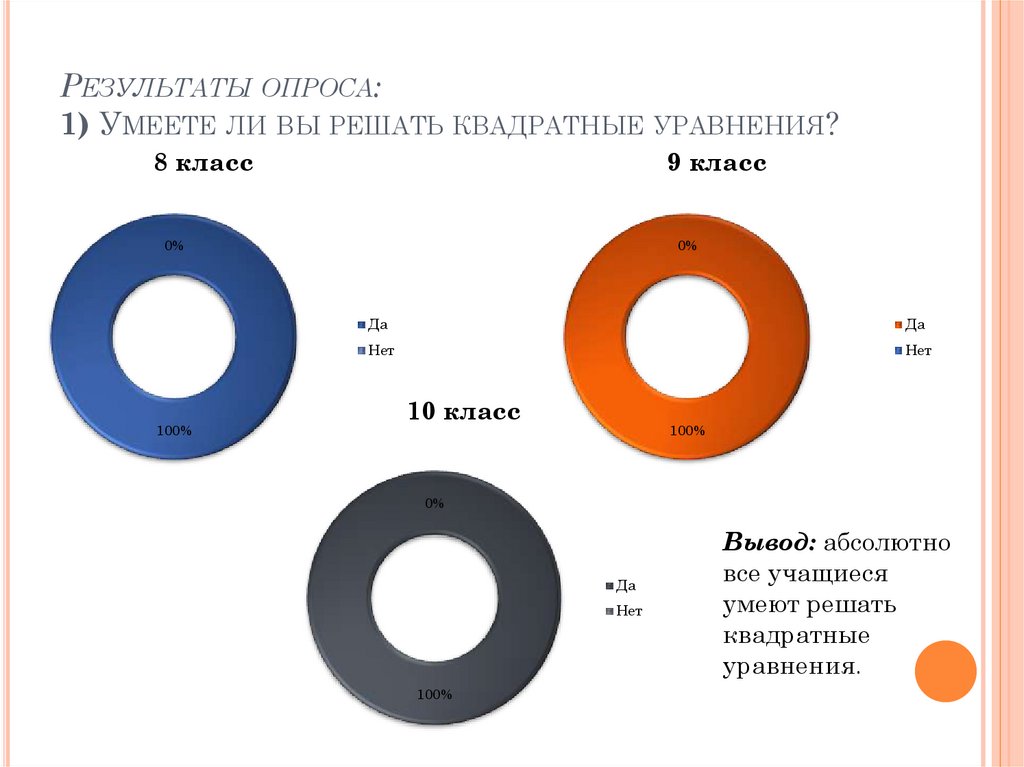
РЕЗУЛЬТАТЫ ОПРОСА:1) УМЕЕТЕ ЛИ ВЫ РЕШАТЬ КВАДРАТНЫЕ УРАВНЕНИЯ?
8 класс
9 класс
0%
100%
0%
Да
Да
Нет
Нет
10 класс
100%
0%
Да
Нет
100%
Вывод: абсолютно
все учащиеся
умеют решать
квадратные
уравнения.
9.
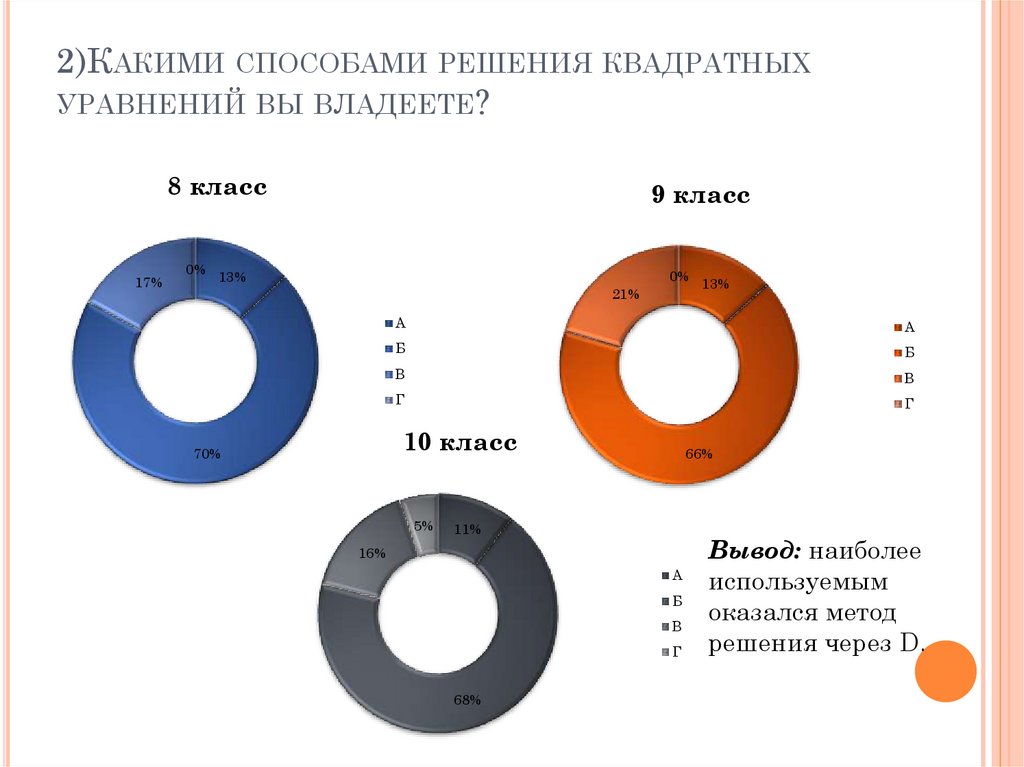
2)КАКИМИ СПОСОБАМИ РЕШЕНИЯ КВАДРАТНЫХУРАВНЕНИЙ ВЫ ВЛАДЕЕТЕ?
8 класс
17%
0%
9 класс
0%
13%
21%
А
А
Б
Б
В
В
Г
Г
10 класс
70%
13%
5%
66%
11%
16%
А
Б
В
Г
68%
Вывод: наиболее
используемым
оказался метод
решения через D.
10.
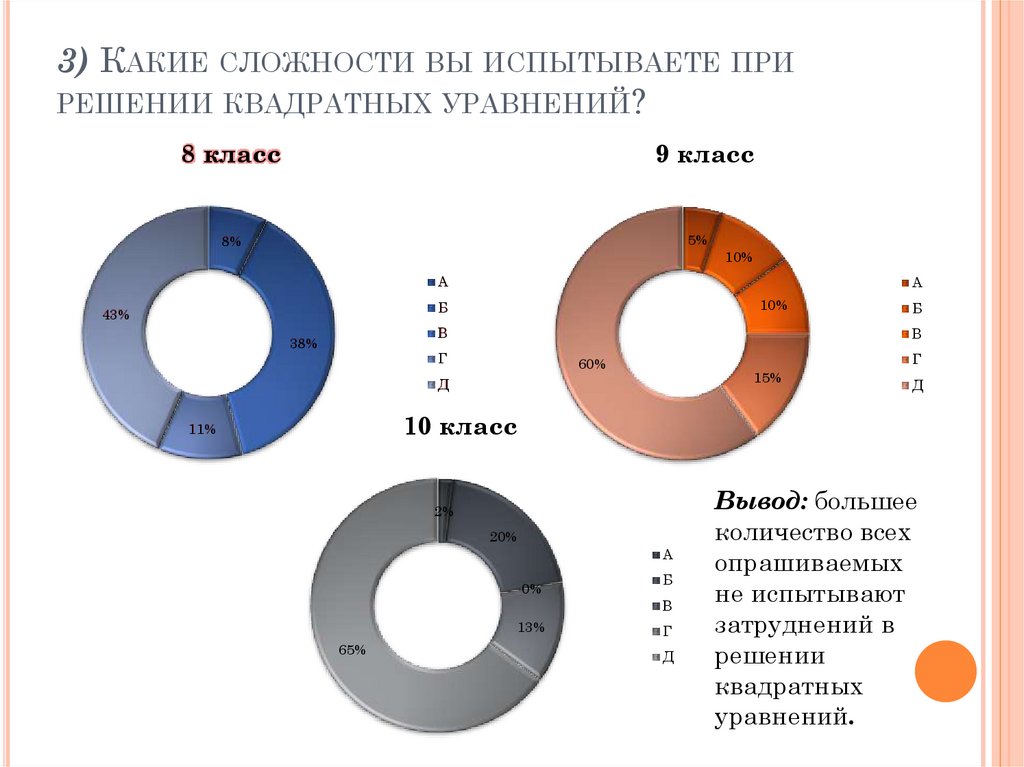
3) КАКИЕ СЛОЖНОСТИ ВЫ ИСПЫТЫВАЕТЕ ПРИРЕШЕНИИ КВАДРАТНЫХ УРАВНЕНИЙ?
8 класс
9 класс
5%
8%
10%
А
А
10%
Б
43%
В
38%
Б
В
Г
Г
60%
15%
Д
Д
10 класс
11%
2%
20%
А
0%
Б
В
13%
65%
Г
Д
Вывод: большее
количество всех
опрашиваемых
не испытывают
затруднений в
решении
квадратных
уравнений.
11.
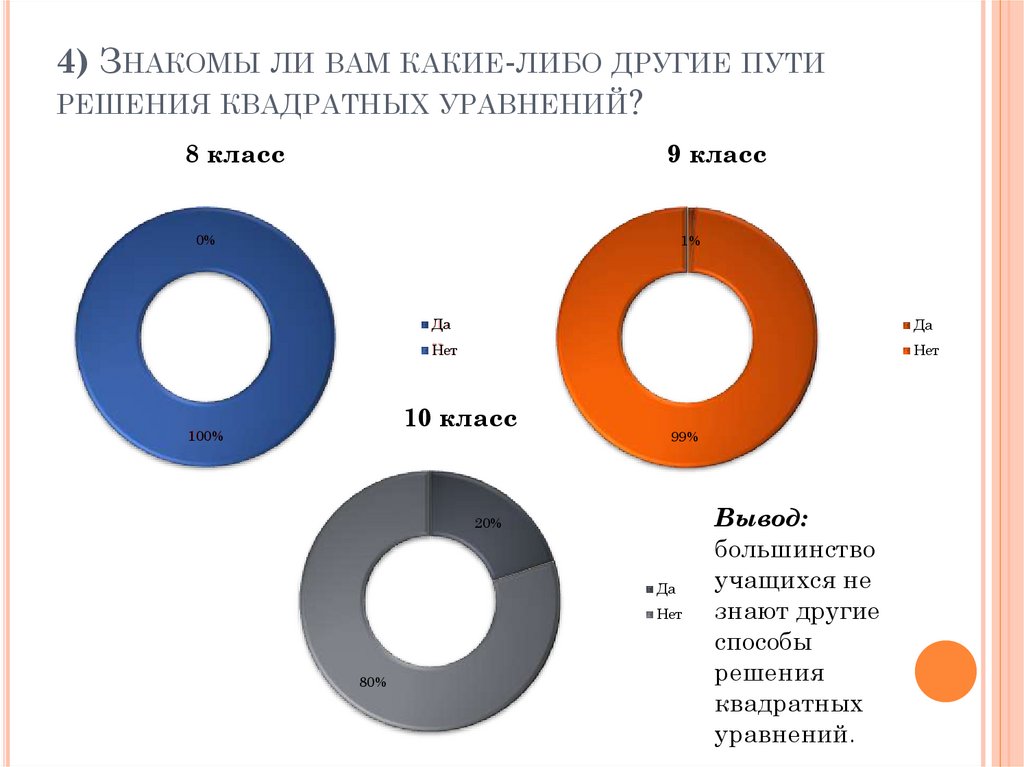
4) ЗНАКОМЫ ЛИ ВАМ КАКИЕ-ЛИБО ДРУГИЕ ПУТИРЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ?
8 класс
9 класс
0%
1%
Да
Да
Нет
Нет
10 класс
100%
99%
20%
Да
Нет
80%
Вывод:
большинство
учащихся не
знают другие
способы
решения
квадратных
уравнений.
12.
2. ИЗ ИСТОРИИ КВАДРАТНЫХ УРАВНЕНИЙ2.1.КВАДРАТНЫЕ УРАВНЕНИЯ В ДРЕВНЕМ
ВАВИЛОНЕ
Квадратные уравнения умели решать около
2000 лет до нашей эры вавилоняне. Применяя
современную алгебраическую запись, можно
сказать, что в их клинописных текстах
встречаются, кроме неполных, и такие,
например, полные квадратные уравнения:
13.
В«Арифметике»
Диофанта нет
систематического
изложения алгебры,
однако в ней
содержится
систематизированный
ряд задач,
сопровождаемых
объяснениями и
решаемых при
помощи составления
уравнений разных
степеней.
14.
2.2. КВАДРАТНЫЕ УРАВНЕНИЯ В ИНДИИИндийский
ученый, Брахмагупта (VII
в.), изложил общее правило решения
квадратных уравнений, приведенных к
единой канонической форме:
15.
В алгебраическом трактате Аль-Хорезми даетсяклассификация линейных и квадратных
уравнений. Автор излагает способы решения
указанных уравнений, пользуясь приемами алджабр и ал-мукабала.
16.
2.3. КВАДРАТНЫЕ УРАВНЕНИЯ В ЕВРОПЕ XIIXVII В.Формы решения квадратных уравнений по образцу
Аль-Хорезми в Европе были впервые изложены в
«Книге абака», написанной в
1202г. итальянским
математиком Леонардом
Фибоначчи.
17.
Общееправило
решения квадратных
уравнений,
приведенных к
единому
каноническому
виду
при всевозможных
комбинациях знаков и
коэффициентов b, c,
было сформулировано
в Европе в 1544 г. М.
Штифелем.
18.
3. СПОСОБЫРЕШЕНИЯ КВАДРАТНЫХ
УРАВНЕНИЙ
3.1. СТАНДАРТНЫЕ СПОСОБЫ
Квадратное
уравнение — это
алгебраическое уравнение общего
вида:
ax² + bx + c = 0
где — x свободная переменная, a, b
и c — коэффициенты, причём a≠0 .
19.
1. РЕШЕНИЕ ЧЕРЕЗ ДИСКРИМИНАНТ, при этом
1)Если D > 0, то квадратное уравнение
имеет два различных корня, которые
находятся по формуле:
2)Если
D = 0, то квадратное уравнение
имеет два одинаковых корня:
3)Если
нет.
D < 0, то действительных корней
20.
2. РЕШЕНИЕ ЧЕРЕЗ D1где
, отсюда формула
нахождения корней:
21.
3. РЕШЕНИЕ ЧЕРЕЗ ТЕОРЕМУ ВИЕТАПо теореме Виета в уравнении
сумма корней равна его второму
коэффициенту, взятому с
противоположным знаком, а
произведение – свободному члену.
22.
3.2. НЕСТАНДАРТНЫЕ СПОСОБЫ1. РЕШЕНИЕ УРАВНЕНИЙ СПОСОБОМ
«ПЕРЕБРОСКИ».
ах2 + bх + с = 0, где а ≠ 0
а2х2 + аbх + ас = 0
Пусть ах = у, откуда х =
у2 + by + ас = 0
Его корни у1 и у2 найдем с помощью теоремы
Виета.
Окончательно получаем:
23.
РЕШЕНИЕ УРАВНЕНИЙ СПОСОБОМ«ПЕРЕБРОСКИ».
Ответ: 4; 3,5
Ответ: 1,75; 2
24.
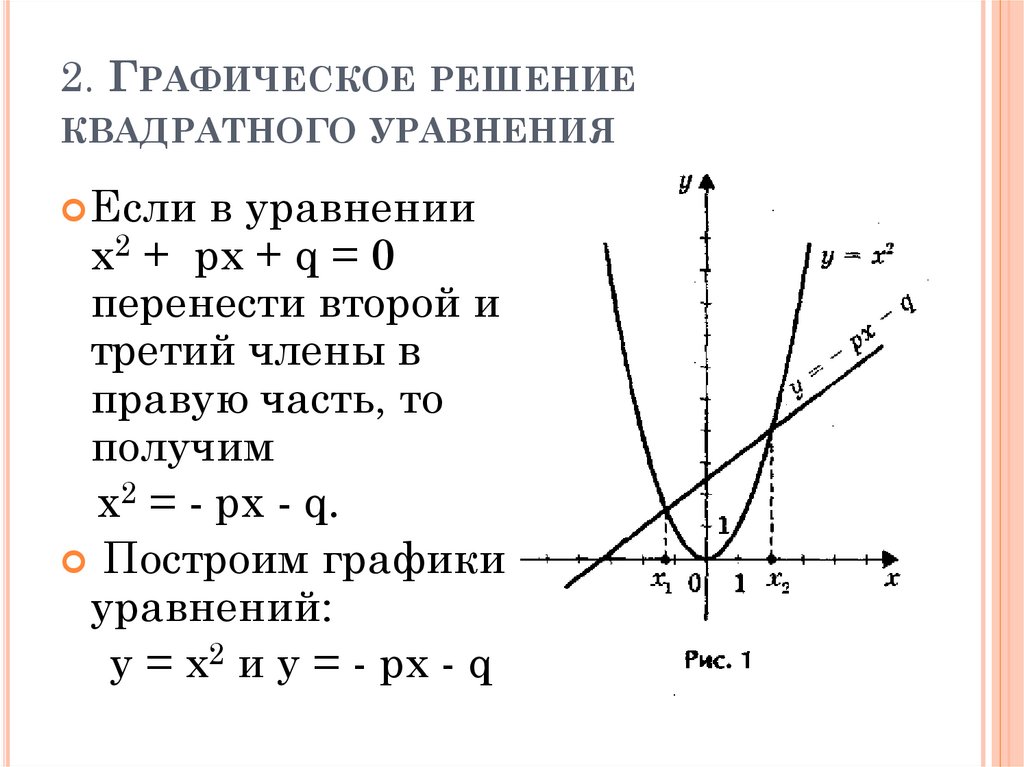
2. ГРАФИЧЕСКОЕ РЕШЕНИЕКВАДРАТНОГО УРАВНЕНИЯ
Если в уравнении
х2 + px + q = 0
перенести второй и
третий члены в
правую часть, то
получим
х2 = - px - q.
Построим графики
уравнений:
у = х2 и у = - px - q
25.
ПРИМЕРЫ1) Решим графически
уравнение х2 - 3х - 4 = 0 (рис.
2).
Решение. Запишем уравнение
в виде х2 = 3х + 4.
Построим параболу у = х2 и
прямую у = 3х + 4.
Прямая и парабола
пересекаются в двух точках
А и В с абсциссами х1 = - 1 и х2
= 4.
Ответ: х1 = - 1; х2 = 4.
26.
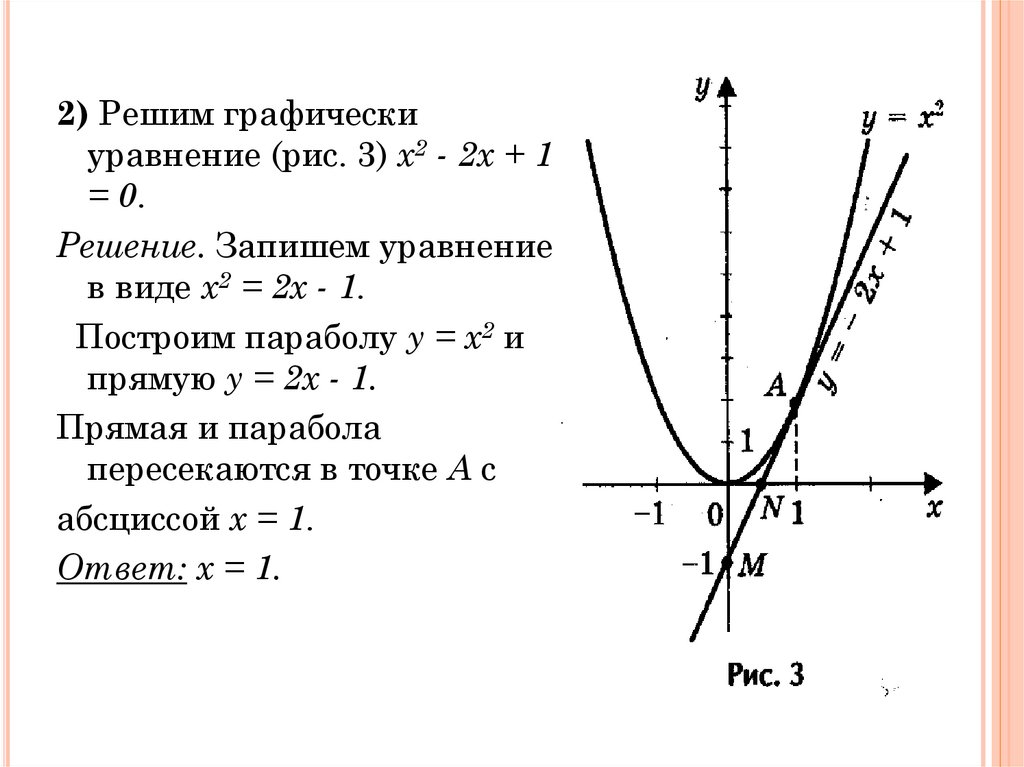
2) Решим графическиуравнение (рис. 3) х2 - 2х + 1
= 0.
Решение. Запишем уравнение
в виде х2 = 2х - 1.
Построим параболу у = х2 и
прямую у = 2х - 1.
Прямая и парабола
пересекаются в точке А с
абсциссой х = 1.
Ответ: х = 1.
27.
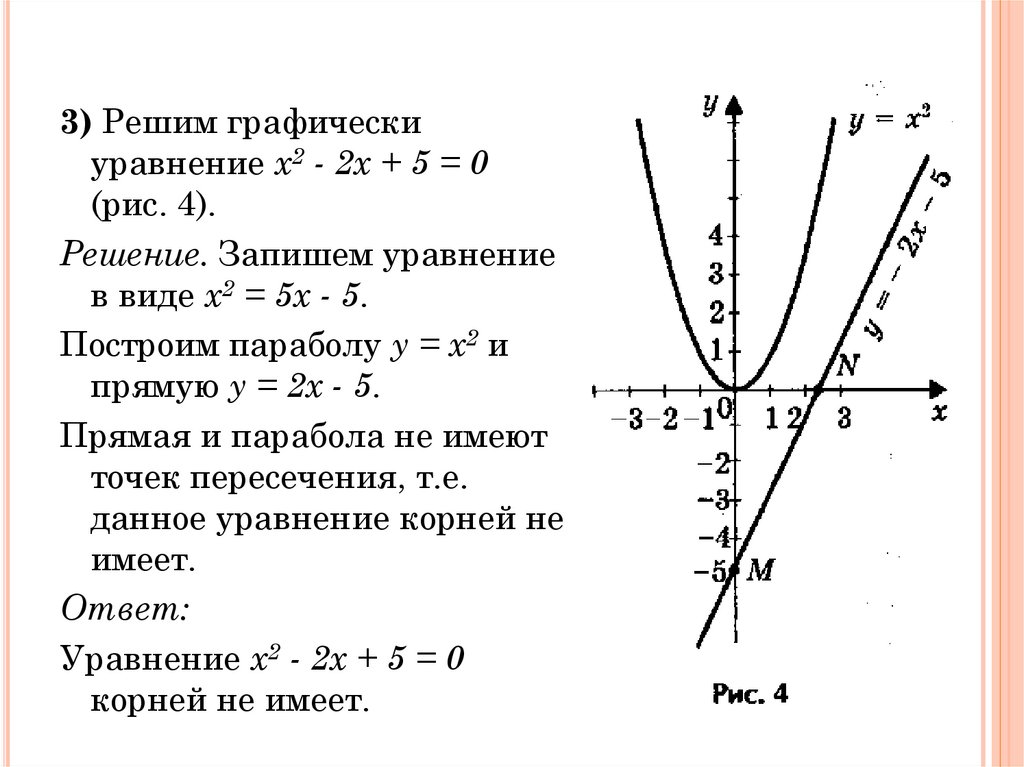
3) Решим графическиуравнение х2 - 2х + 5 = 0
(рис. 4).
Решение. Запишем уравнение
в виде х2 = 5х - 5.
Построим параболу у = х2 и
прямую у = 2х - 5.
Прямая и парабола не имеют
точек пересечения, т.е.
данное уравнение корней не
имеет.
Ответ:
Уравнение х2 - 2х + 5 = 0
корней не имеет.
28.
3. ПРИ ПОМОЩИ СВОЙСТВ КОЭФФИЦИЕНТОВКВАДРАТНОГО УРАВНЕНИЯ.
Дано квадратное
уравнение
2
ах +
где а ≠ 0
bх + с = 0,
29.
.1) ЕСЛИ
, ТО
Так как a + b + c = 0 то b = – (a + c).
В уравнение ax² + bx + c = 0
подставим b = – (a + c), получим:
ax² – ( a + c)x + c = 0
(ax² – ax) – (cx – x) = 0
ax(x – 1) – c(ax – c) = 0
(x – 1)(ax – c) = 0
x – 1 = 0 и ax – c = 0
30.
ПРИ ПОМОЩИ СВОЙСТВ КОЭФФИЦИЕНТОВКВАДРАТНОГО УРАВНЕНИЯ
31.
2) ЕСЛИТО
В уравнение ax² + bx + c = 0
подставим b = a + c , получим:
ax² + ( a + c)x + c = 0
(ax² + ax) + (cx + x) = 0
ax(x + 1) + c(ax + c) = 0
(x + 1)(ax + c) = 0
x + 1 = 0 и ax + c = 0
32.
ПРИ ПОМОЩИ СВОЙСТВ КОЭФФИЦИЕНТОВКВАДРАТНОГО УРАВНЕНИЯ
33.
;.3) ЕСЛИ
, ТО
Уравнение принимает вид ax² + (a² + 1)x + a = 0
Подставив b = a² + 1, c = a , по известной нам
формуле находим дискриминант:
Теперь находим корни уравнения:
34.
ПРИ ПОМОЩИ СВОЙСТВ КОЭФФИЦИЕНТОВКВАДРАТНОГО УРАВНЕНИЯ
35.
4. ЗАКЛЮЧЕНИЕКвадратные уравнения находят широкое
применение при решении тригонометрических,
показательных, логарифмических и
иррациональных уравнений и неравенств.
Так как эти методы решения квадратных
уравнений просты в применении, то они,
безусловно, должны заинтересовать
увлекающихся математикой учеников. Наша
работа дает возможность иначе посмотреть на те
задачи, которые ставит перед нами математика.
36.
5. СПИСОК ИНТЕРНЕТ-РЕСУРСОВ1. https://pandia.ru/text/78/002/10610.php
2. https://studfile.net/preview/5430386/
3. https://kopilkaurokov.ru/matematika/uroki/12sposobov-rieshieniia-kvadratnykh-uravnienii
4. http://www.tutoronline.ru/blog/reshenie-kvadratnyhuravnenij-metodom-perebroski.aspx
5. http://www.tutoronline.ru/blog/dec_2011/kvadratnyei-bikvadratnye-uravnenija.aspx















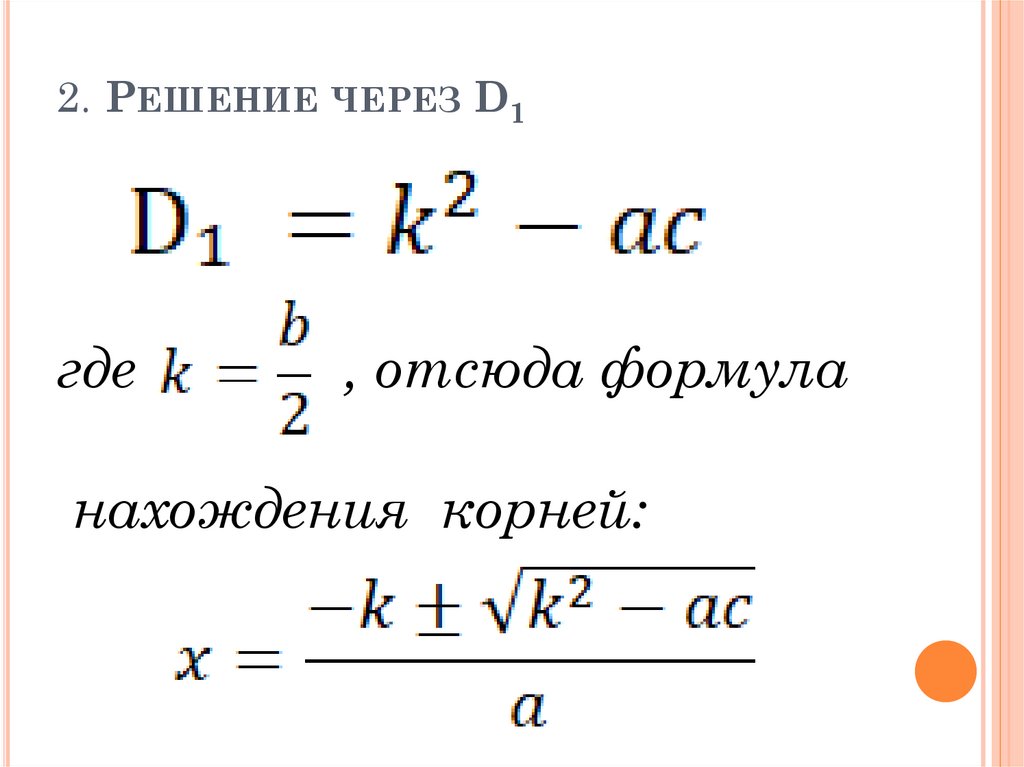





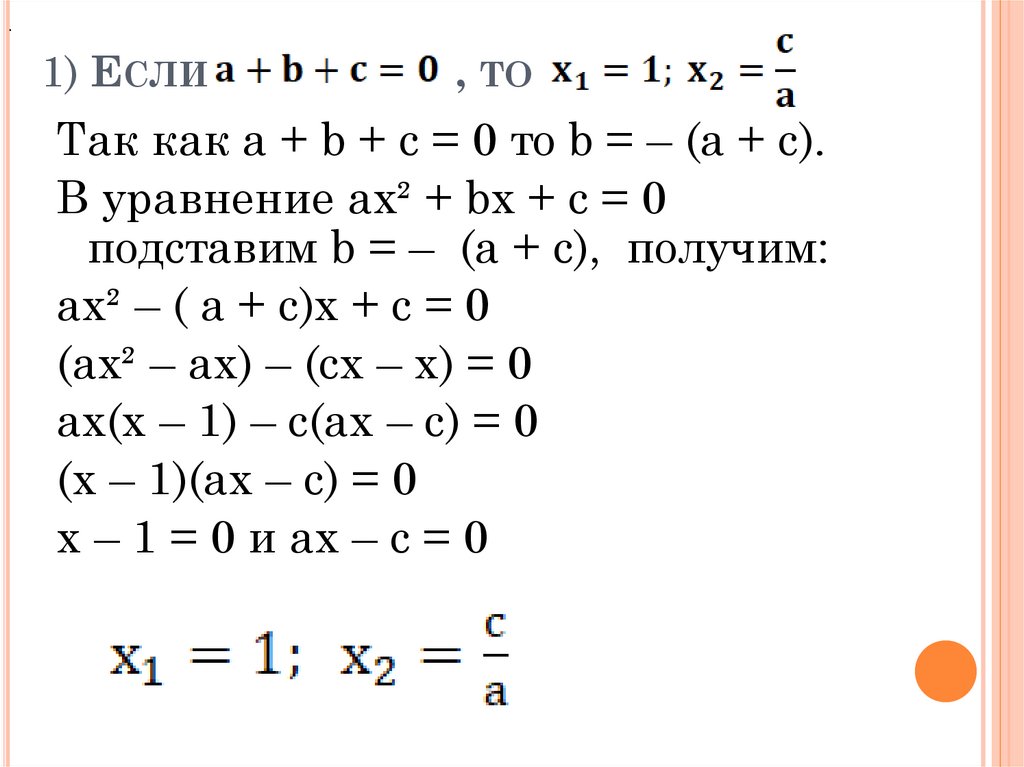

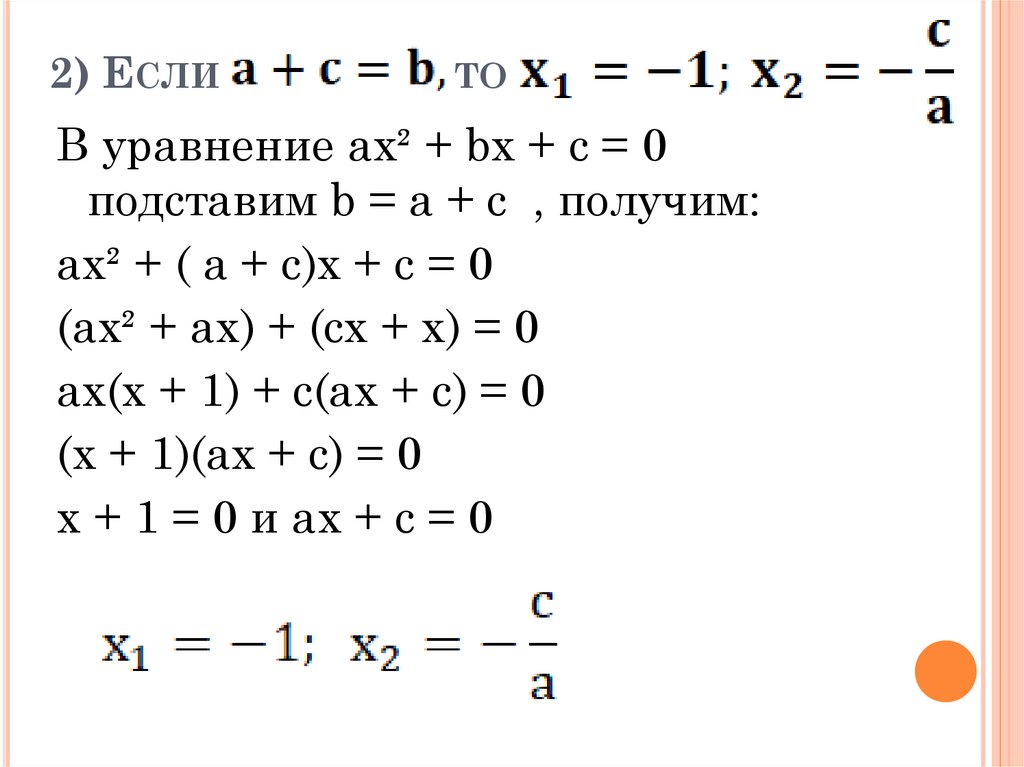





 mathematics
mathematics








