Similar presentations:
Классная работа. Признаки равенства треугольников
1.
2.
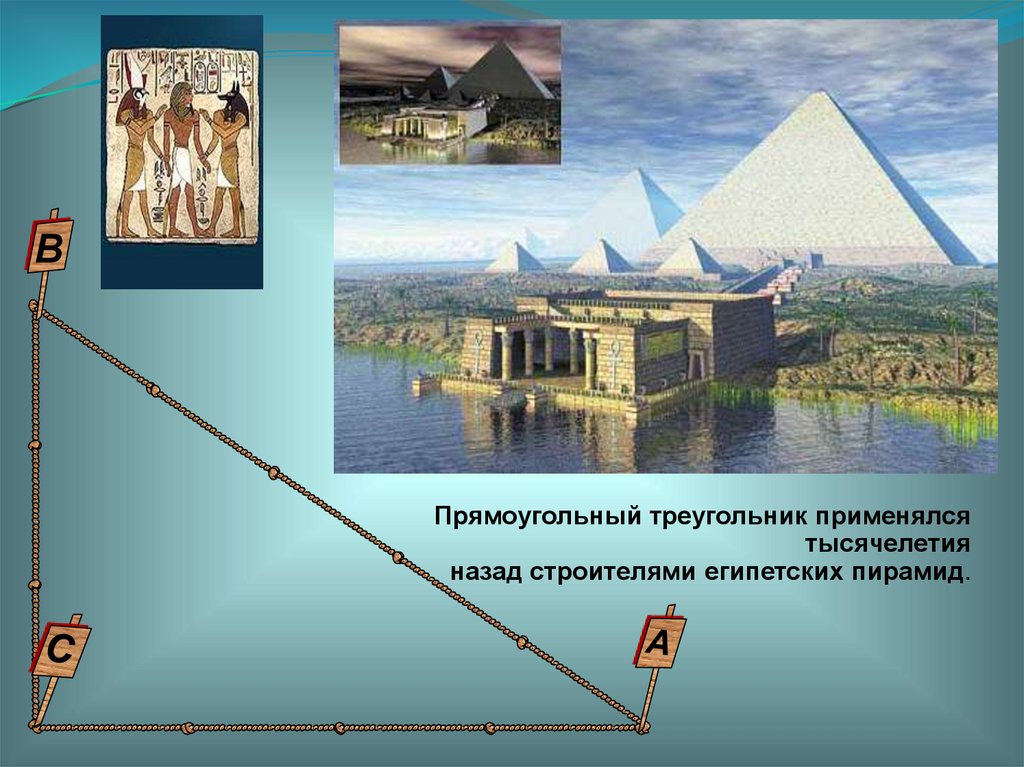
ВПрямоугольный треугольник применялся
тысячелетия
назад строителями египетских пирамид.
3.
Для составления красивых паркетов частоиспользовали треугольники.
4.
Треугольники в конструкции мостов.5.
Высоковольтные линии электропередачи.Треугольники делают конструкции надежными.
6.
Начиная игру в бильярд, необходимо расположитьшары в виде треугольника.
Для этого используют специальную треугольную
рамку.
7.
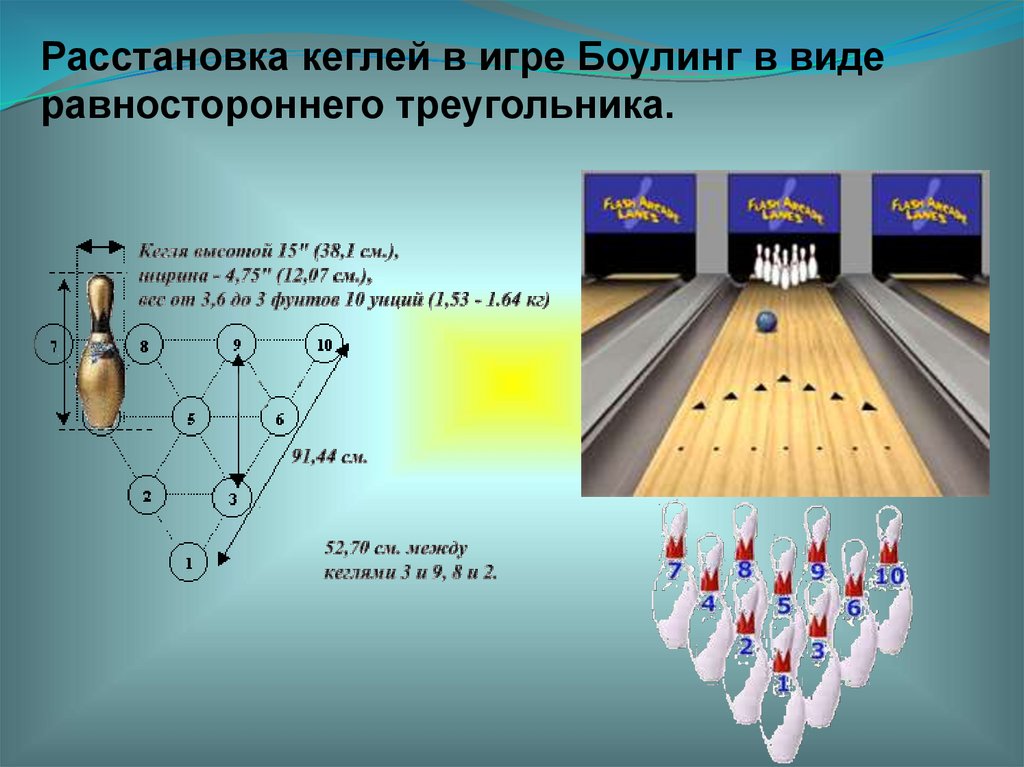
Расстановка кеглей в игре Боулинг в видеравностороннего треугольника.
8.
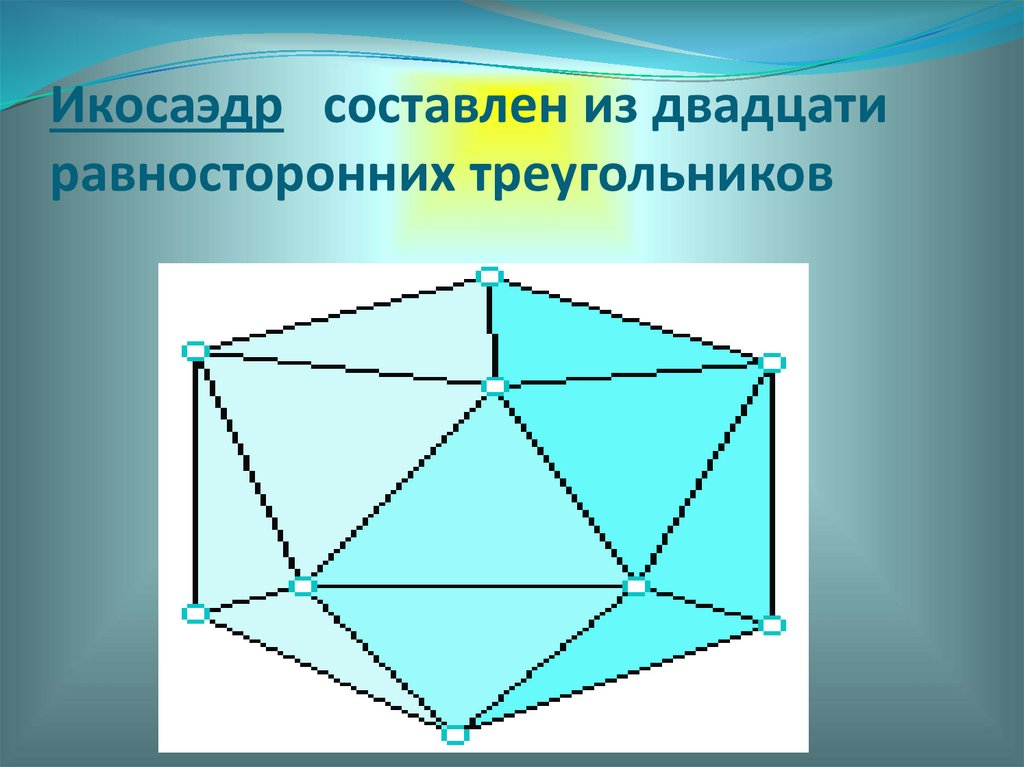
Икосаэдр составлен из двадцатиравносторонних треугольников
9.
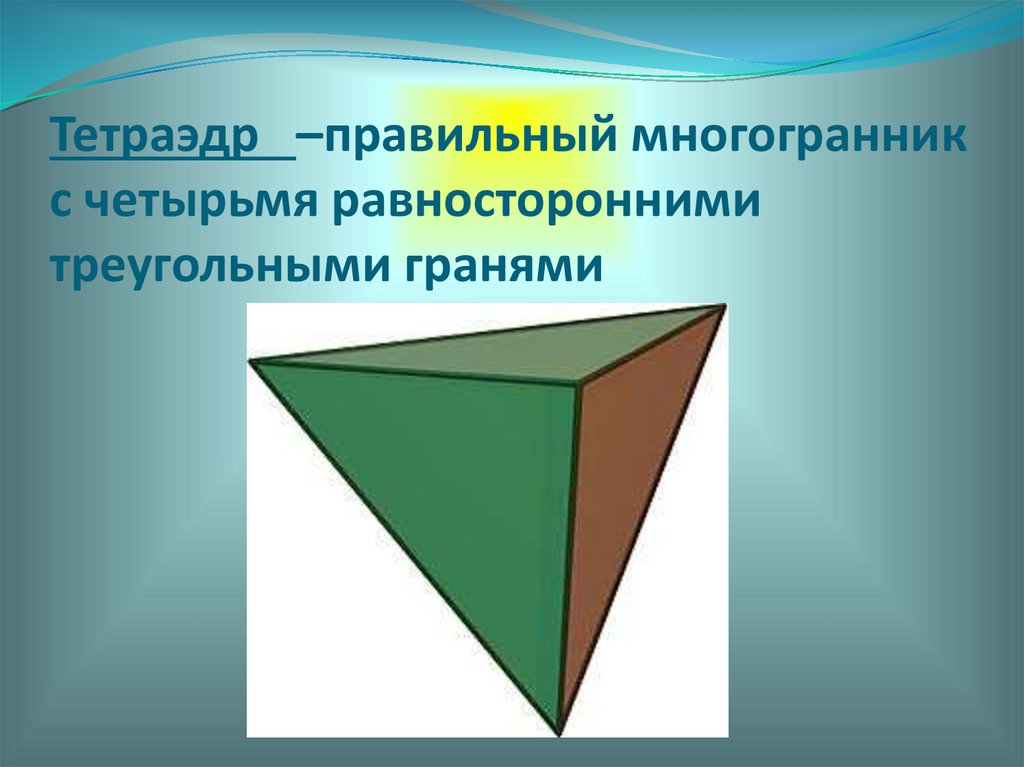
Тетраэдр –правильный многогранникс четырьмя равносторонними
треугольными гранями
10.
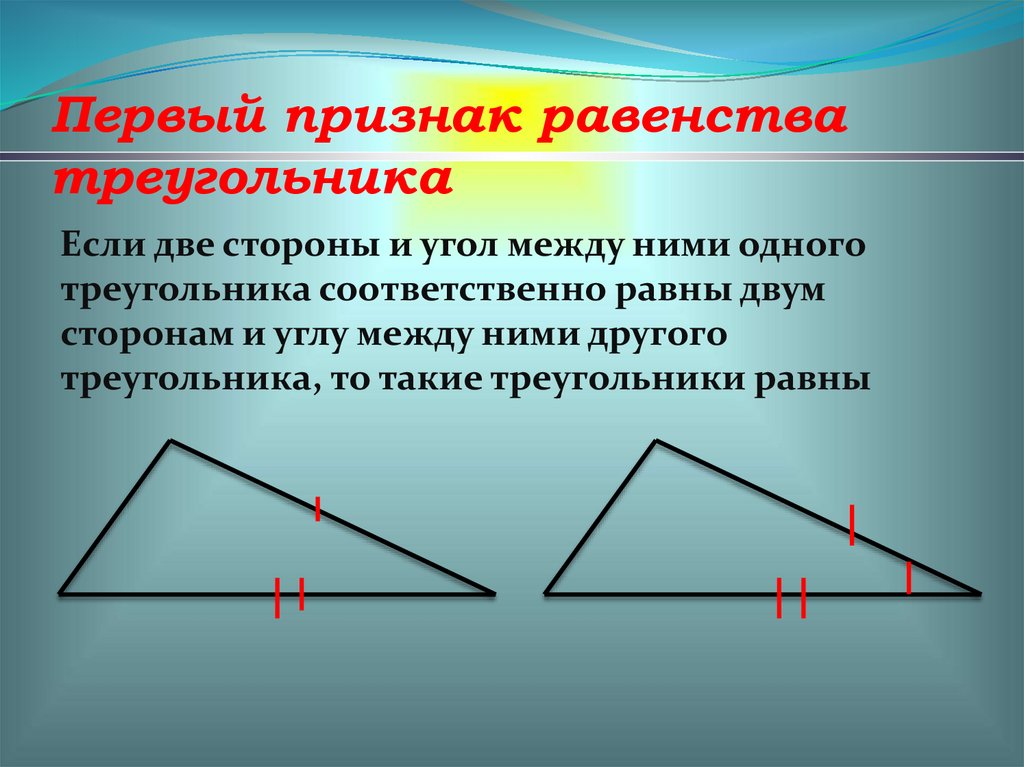
Первый признак равенстватреугольника
Если две стороны и угол между ними одного
треугольника соответственно равны двум
сторонам и углу между ними другого
треугольника, то такие треугольники равны
11.
Второй признак равенстватреугольников
Если сторона и два прилежащих к ней угла одного
треугольника соответственно равны стороне и двум
прилежащим к ней углам другого треугольника, то
такие треугольники равны
12.
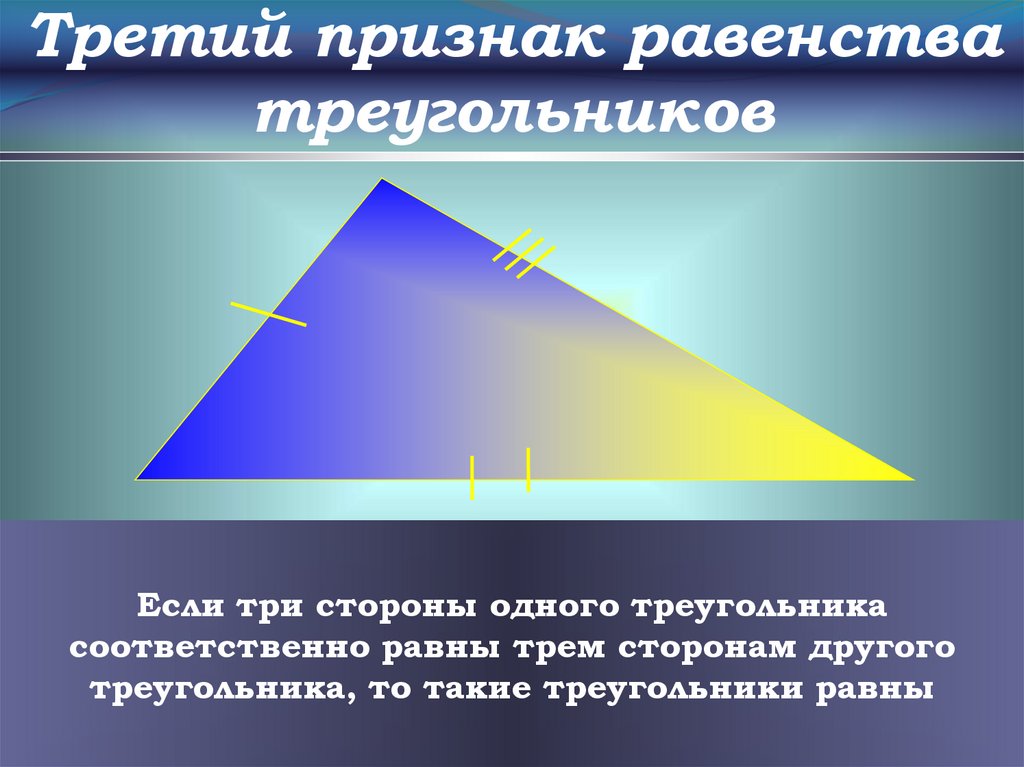
Третий признак равенстватреугольников
Если три стороны одного треугольника
соответственно равны трем сторонам другого
треугольника, то такие треугольники равны
13.
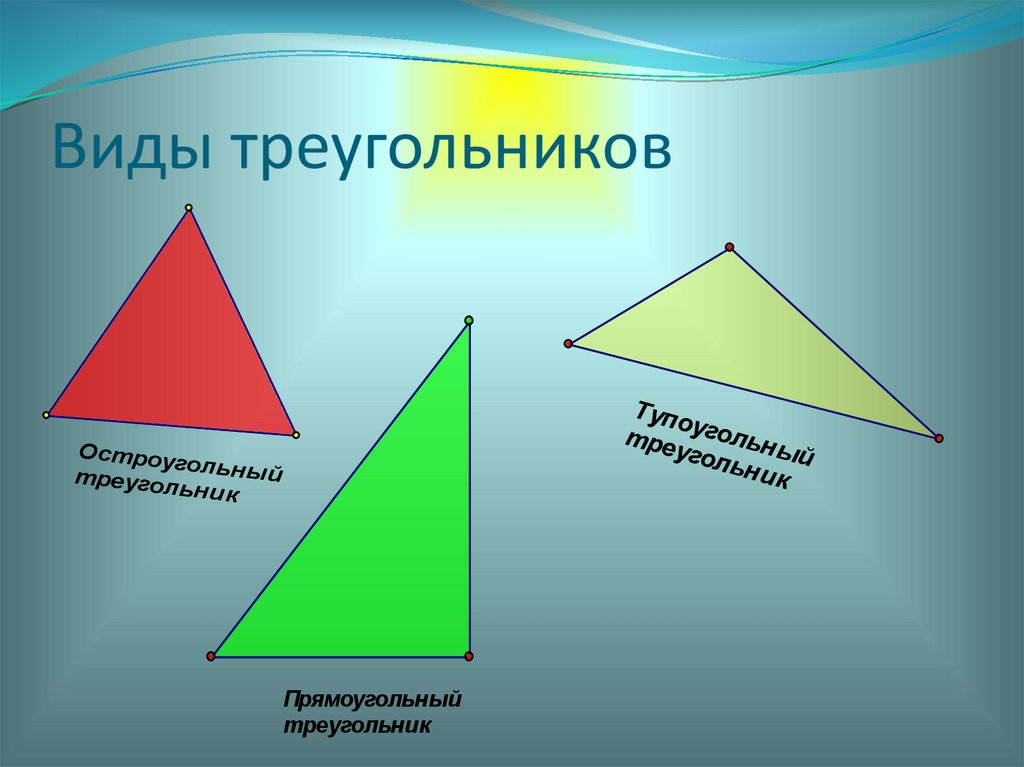
Виды треугольниковТуп
о
тре угольн
ы
угол
ьн и й
к
Остроу
го
треугол льн ый
ьн ик
Прямоугольный
треугольник
14.
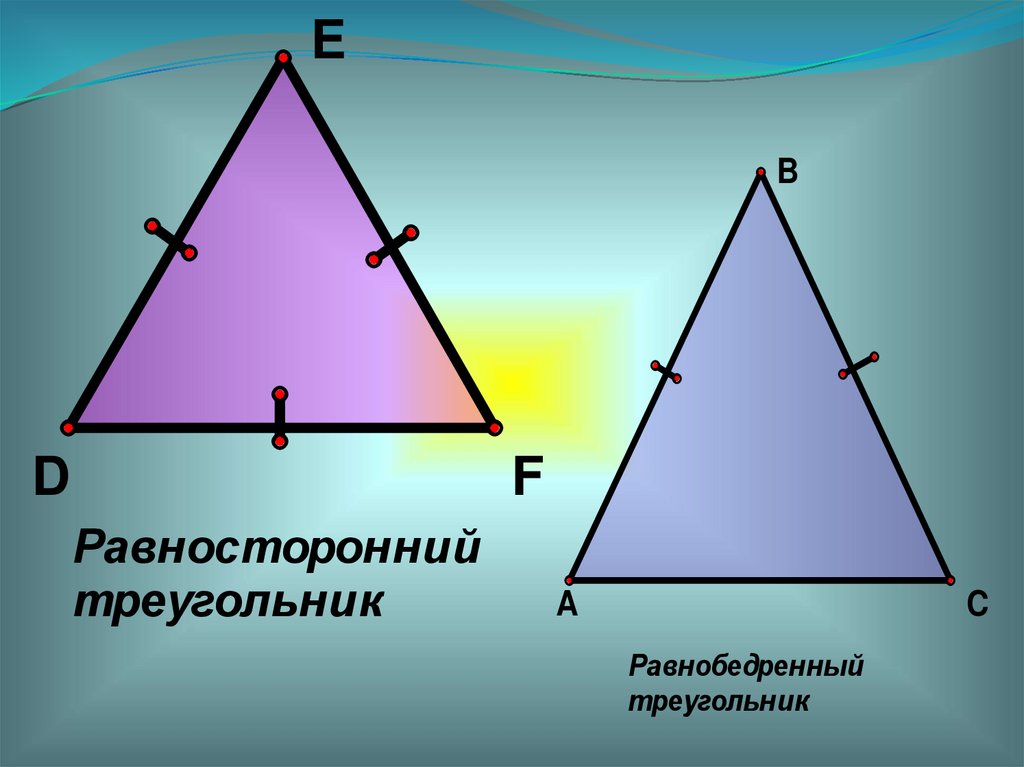
EB
D
F
Равносторонний
треугольник
A
C
Равнобедренный
треугольник
15.
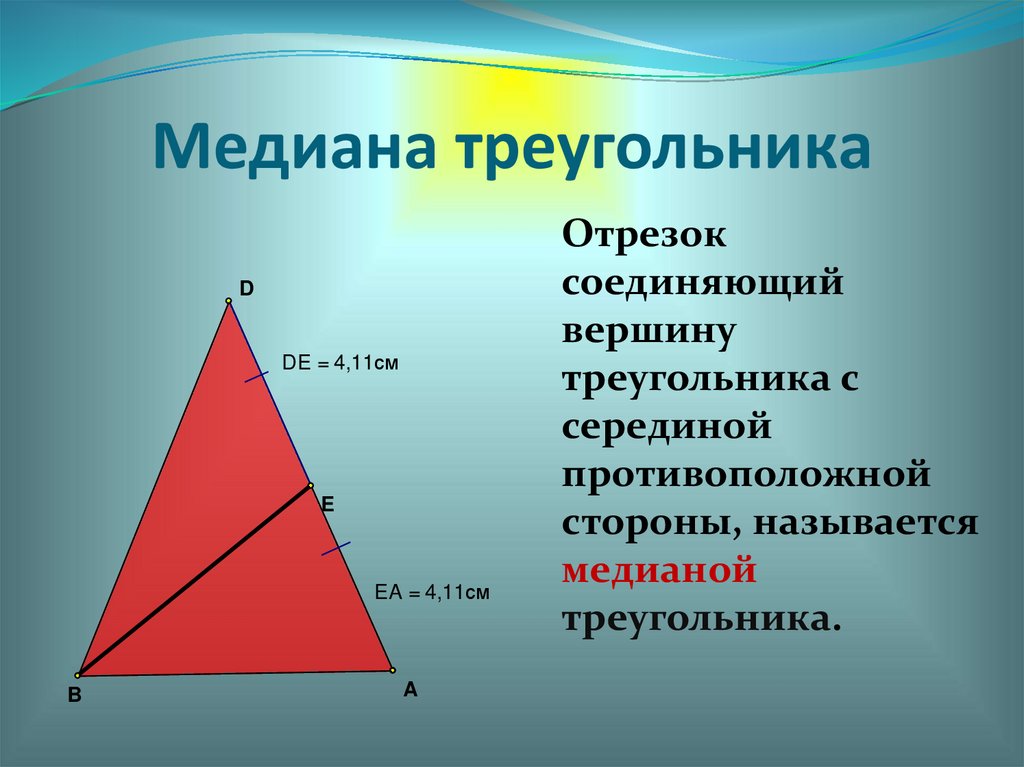
Медиана треугольникаD
DE = 4,11см
E
EA = 4,11см
B
A
Отрезок
соединяющий
вершину
треугольника с
серединой
противоположной
стороны, называется
медианой
треугольника.
16.
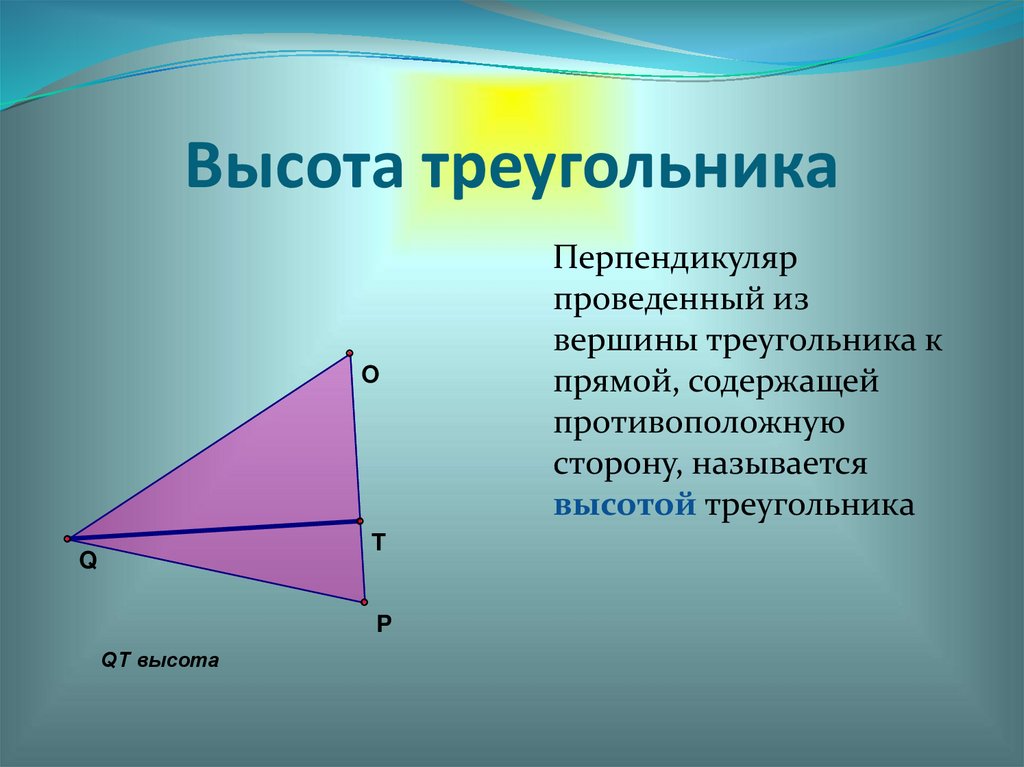
Высота треугольникаO
T
Q
P
QT высота
Перпендикуляр
проведенный из
вершины треугольника к
прямой, содержащей
противоположную
сторону, называется
высотой треугольника
17.
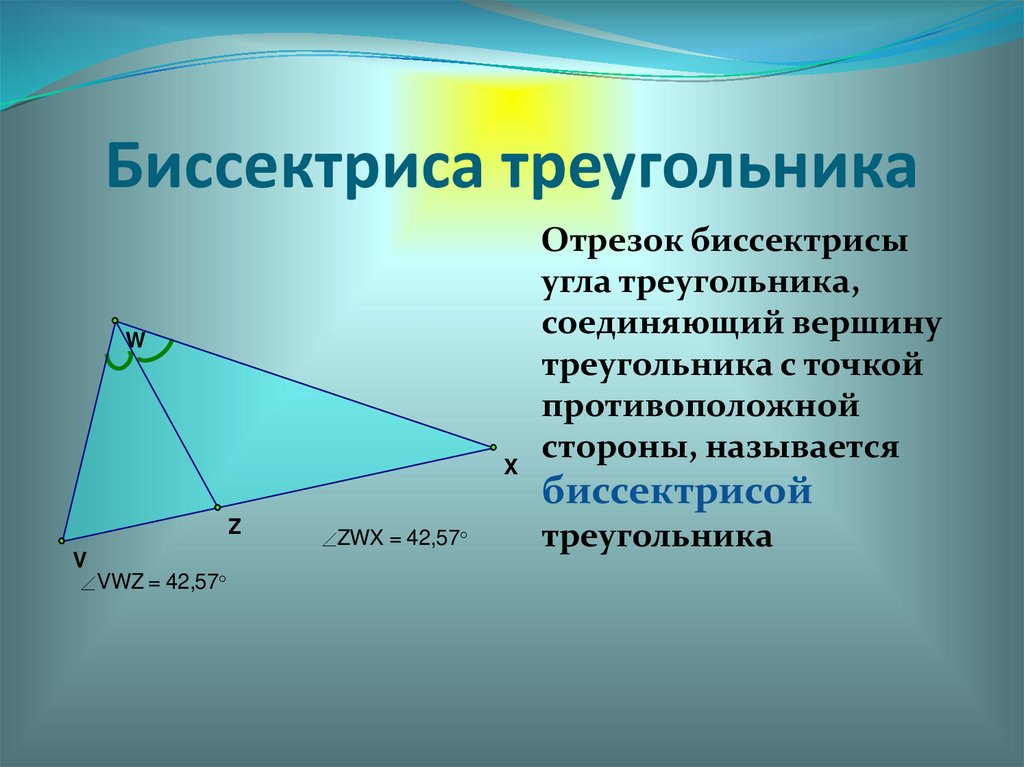
Биссектриса треугольникаW
X
Z
V
VWZ = 42,57
ZWX = 42,57
Отрезок биссектрисы
угла треугольника,
соединяющий вершину
треугольника с точкой
противоположной
стороны, называется
биссектрисой
треугольника
18.
Устная работа19.
20.
21.
22.
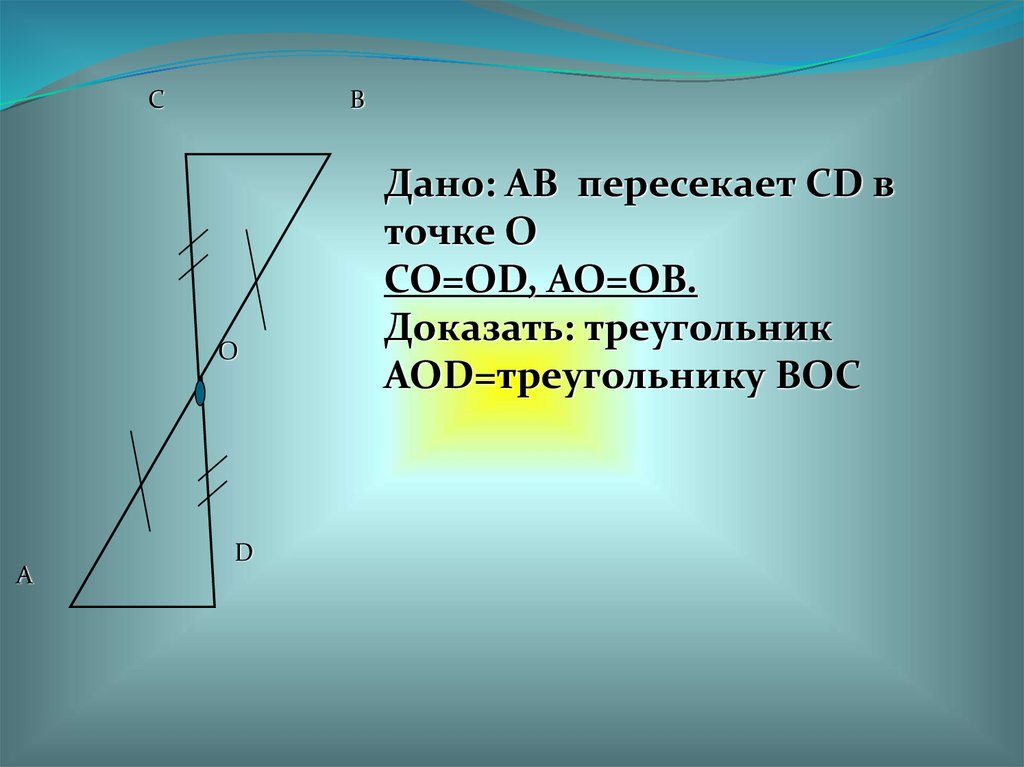
СВ
О
А
D
Дано: AB пересекает CD в
точке О
СО=ОD, АО=ОВ.
Доказать: треугольник
АОD=треугольнику ВОС
23.
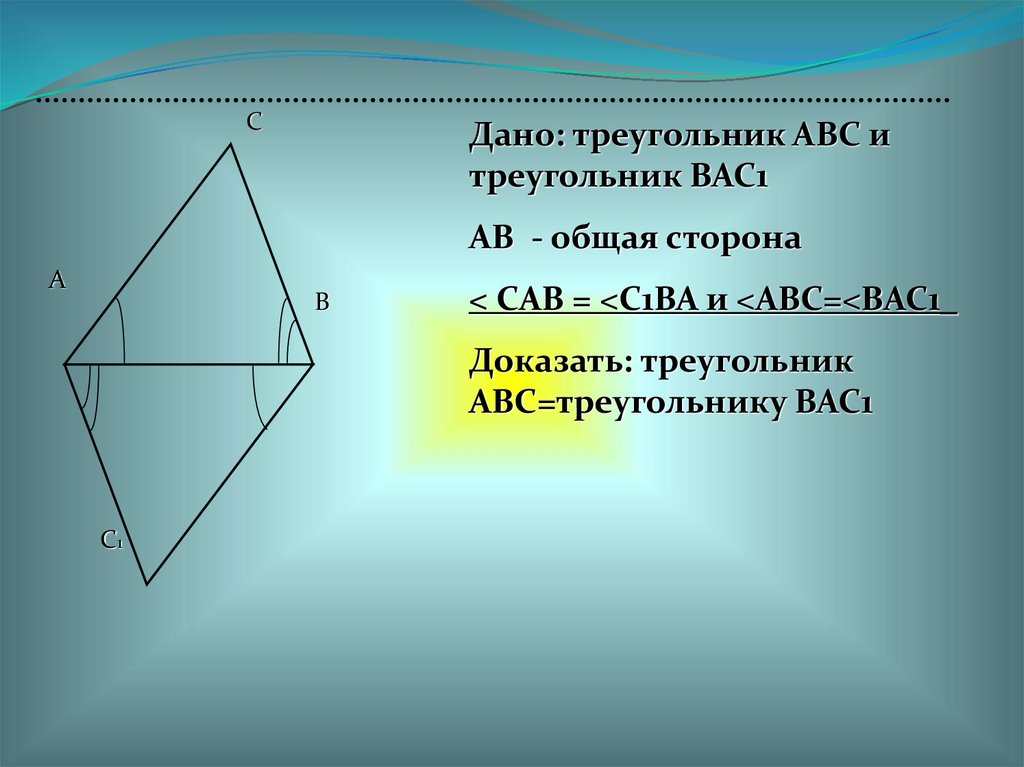
СДано: треугольник АВС и
треугольник ВАС1
AB - общая сторона
А
В
< САВ = <С1ВА и <АВС=<ВАС1_
Доказать: треугольник
АВС=треугольнику ВАС1
С1
24.
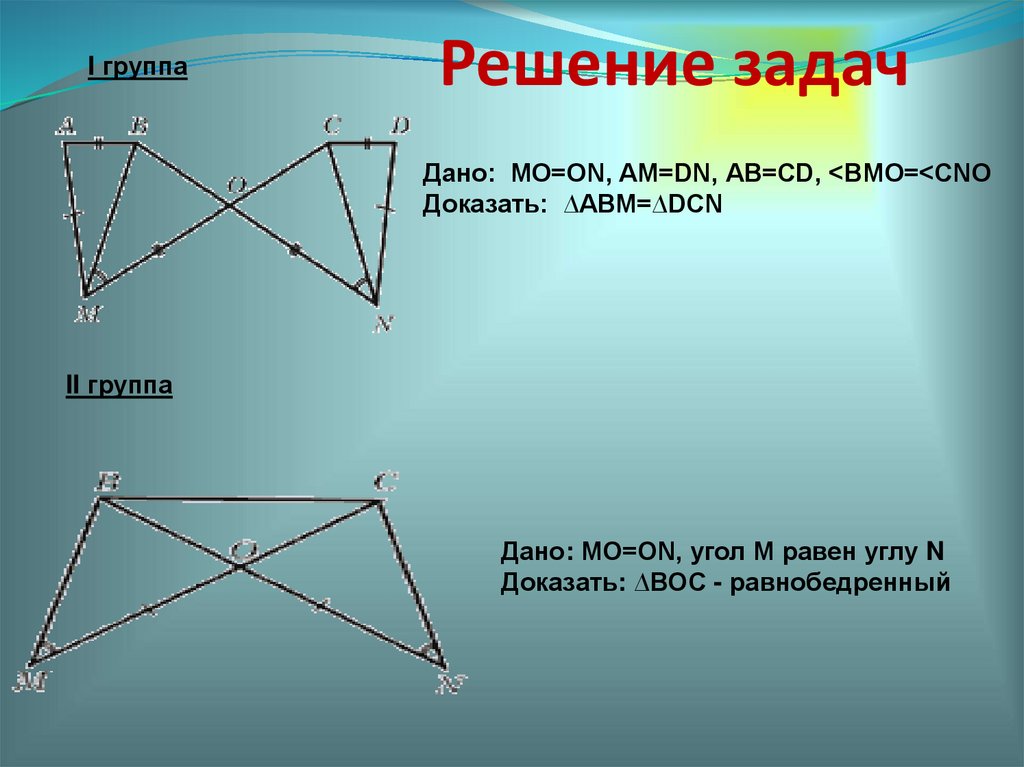
I группаРешение задач
Дано: МО=ОN, АМ=DN, АВ=СD, <ВМО=<СNО
Доказать: ∆АВМ=∆DСN
II группа
Дано: МО=ОN, угол М равен углу N
Доказать: ∆ВОС - равнобедренный
25.
I группаII группа
26.
27.
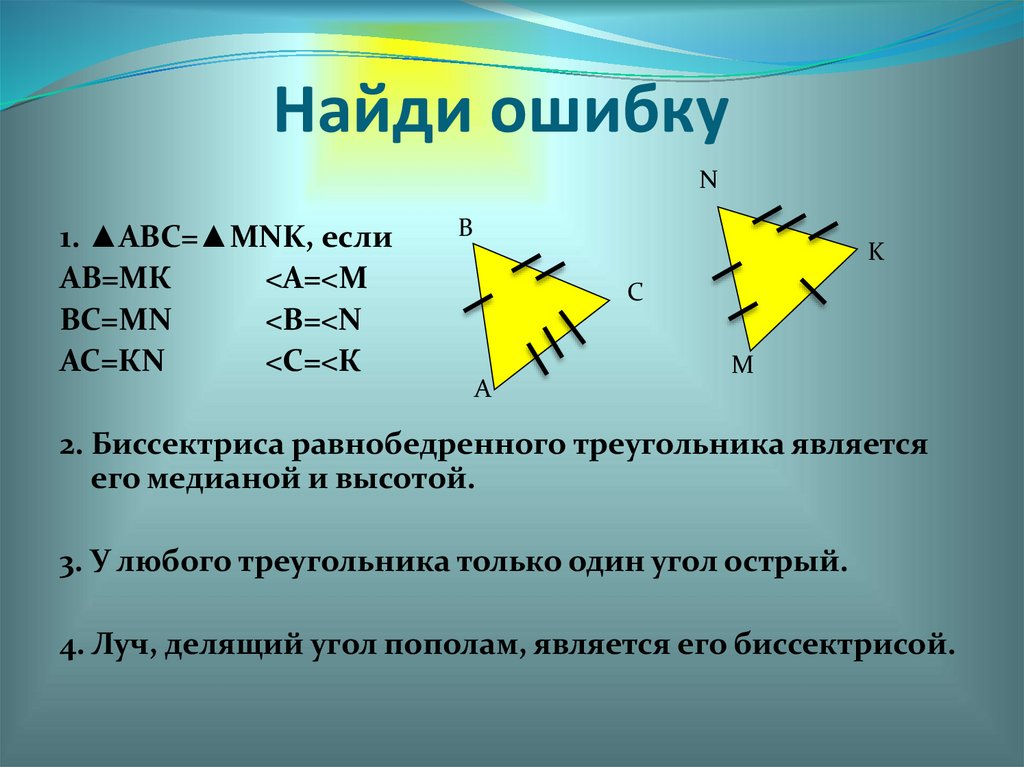
Найди ошибкуN
1. ▲ABC=▲MNK, если
АВ=МК
<А=<М
ВС=МN
<В=<N
АС=КN
<С=<К
В
K
С
А
М
2. Биссектриса равнобедренного треугольника является
его медианой и высотой.
3. У любого треугольника только один угол острый.
4. Луч, делящий угол пополам, является его биссектрисой.
28.
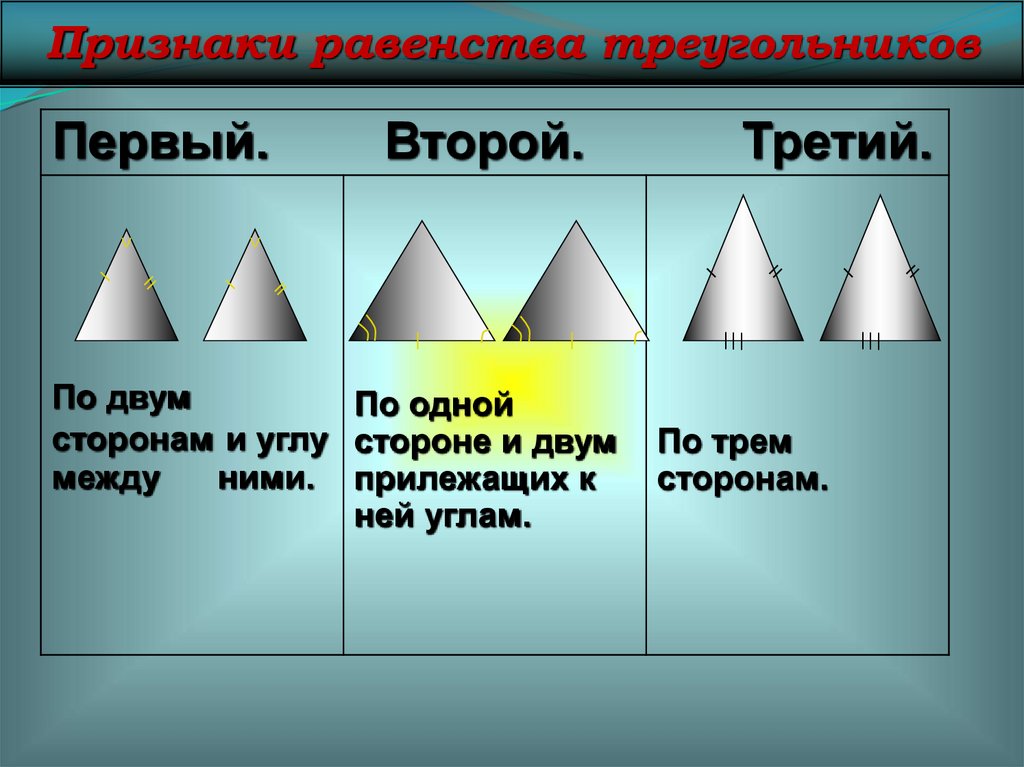
Признаки равенства треугольниковПервый.
Второй.
По двум
По одной
сторонам и углу стороне и двум
между
ними. прилежащих к
ней углам.
Третий.
По трем
сторонам.
29.
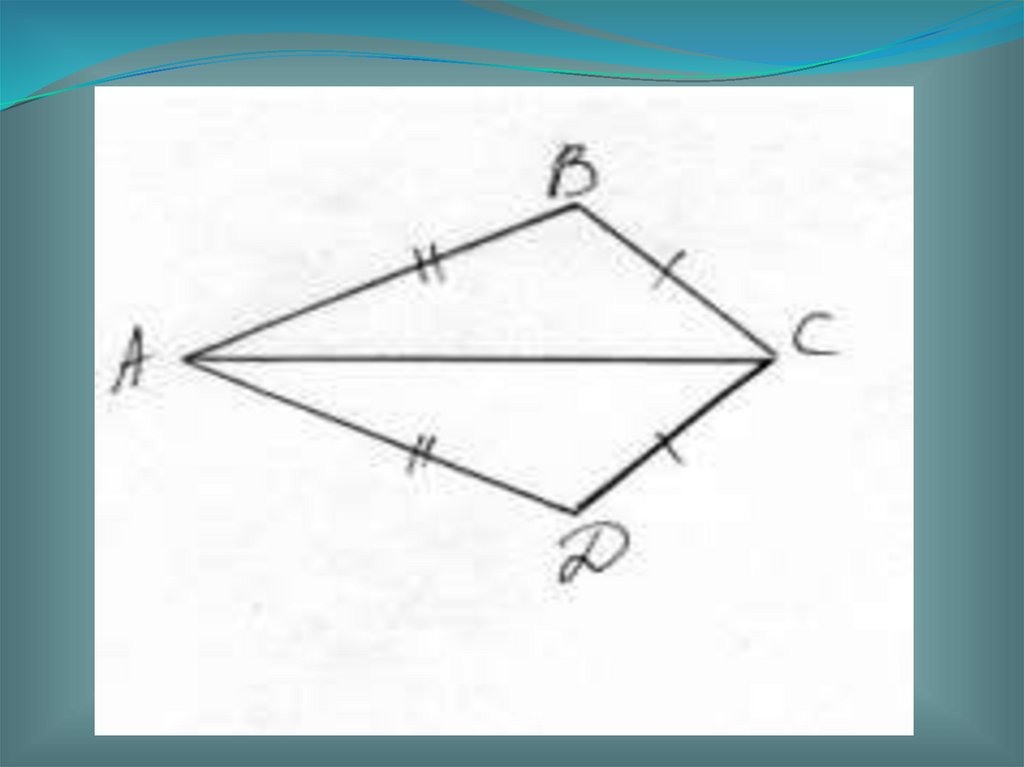
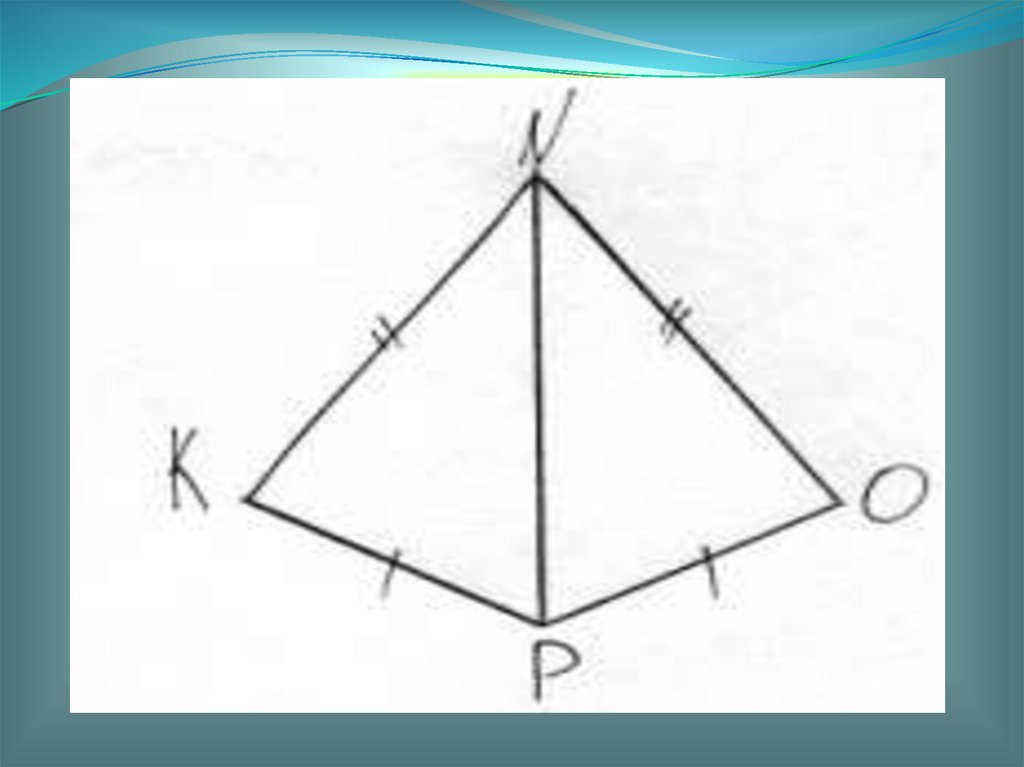
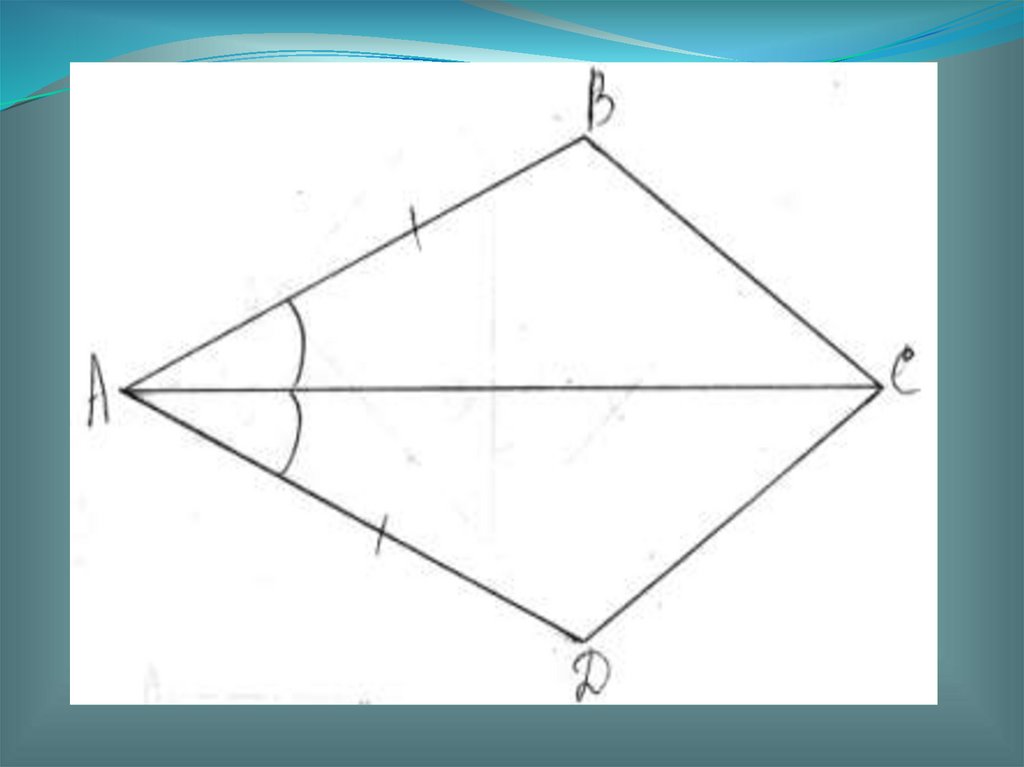
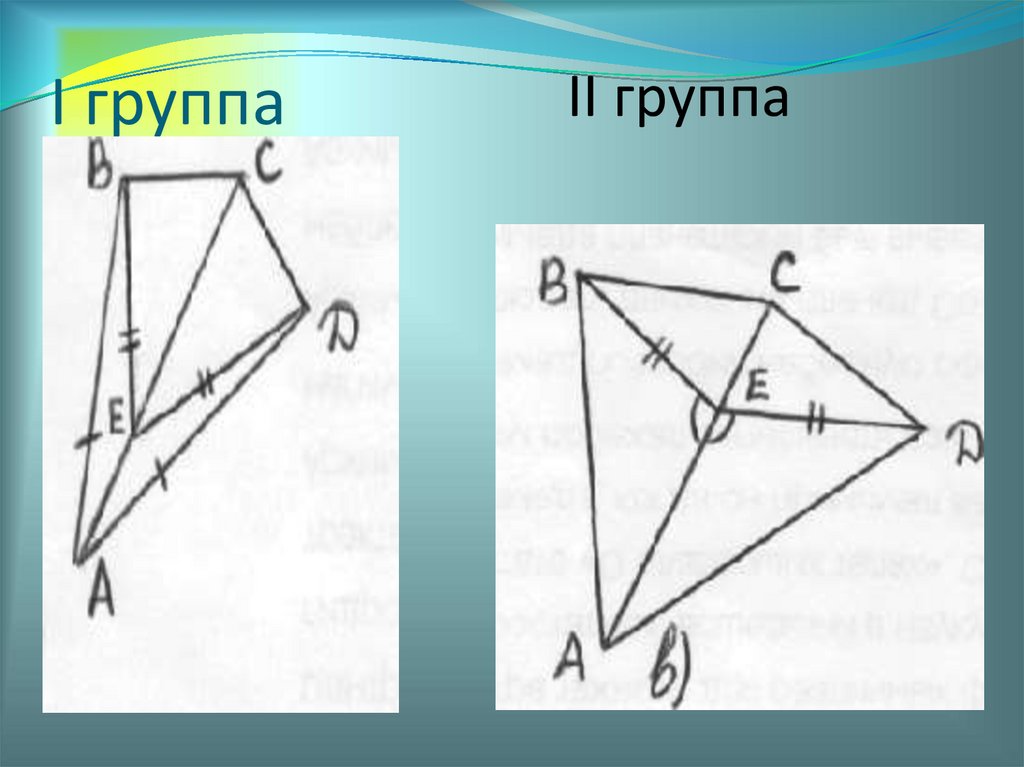
Домашнее задание1. Пункты 14-20 повторить
2. Исследовательская задача (на
листочке)
Исследовать: отметить равные
отрезки и углы, выписать пары
равных треугольников








 mathematics
mathematics pedagogy
pedagogy








