Similar presentations:
Интеграл. Определенный интеграл. Свойства
1.
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГООБРАЗОВАНИЯ РОСТОВСКОЙ ОБЛАСТИ
Государственной бюджетное профессиональное образовательное учреждение Ростовской
области
«Ростовский технологический техникум сервиса»
(ГБПОУ РО «РТТС»)
Тема:"Интеграл. Определенный интеграл. Свойства.
Примеры. Применение определенного интеграла для
нахождения длин, площадей и объемов”
Подготовила:
Обучающаяся группы №17 1 курса
Маилова Айтач
2.
Определенный интеграл.Определенным интегралом функции
y=f(x) на [a,b] называется
,
если этот предел существует и не зависит от
способа разбиений [a,b] на
и от выбора
точек
. Определенный интеграл
обозначается:
Числа a и b
называются соответственно нижним и верхним
пределами интегрирования.
3.
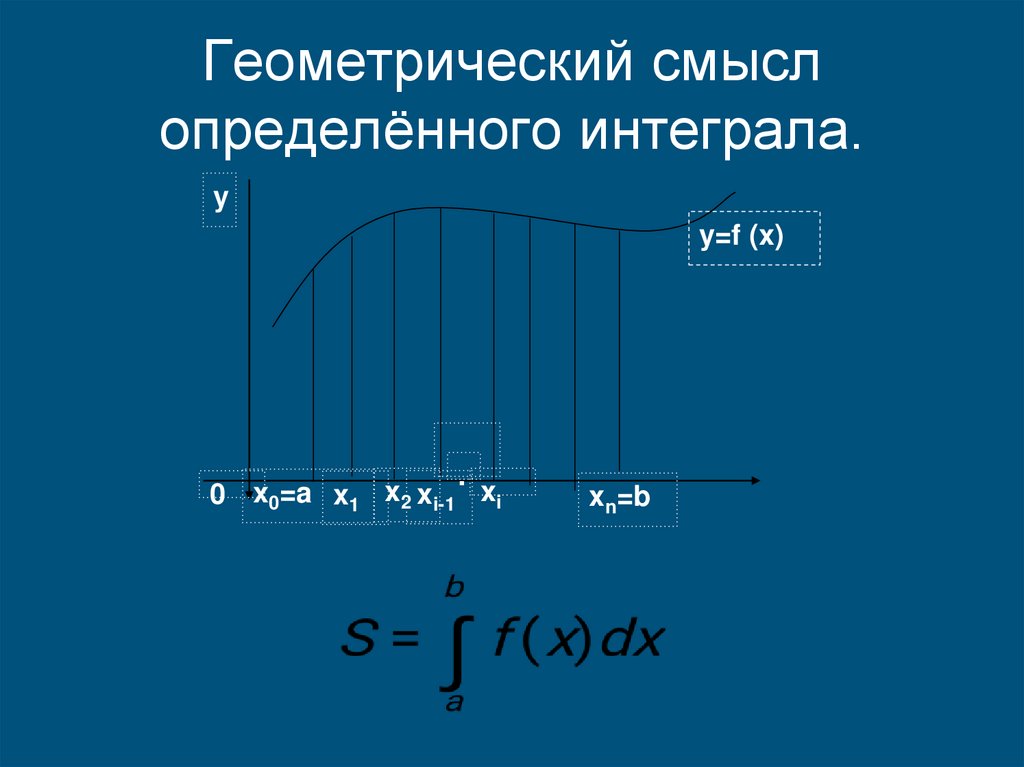
Геометрический смыслопределённого интеграла.
y
y=f (x)
.
0 x0=a x1 x2 xi-1 xi
xn=b
4.
Свойства определённогоинтеграла.
1.
3.
2.
, k-любое число
4.
5.Аддитивность определённого интеграла. Для
любых чисел a,b,c справедливо:
5.
Формула Ньютона-Лейбница.Если F(x) есть какая-либо первообразная
от непрерывной на [ , ] функции f(x), то
справедлива формула
Ньютона-Лейбница:
6.
Пример.7.
Площадь криволинейной трапеции, ограниченнойкривой, заданной параметрически.
8.
, гдеx(t), y(t), x’(t), y’(t) – непрерывны
на
y
0 a
b
x
9.
Пример.Найти площадь фигуры, ограниченной осью OX и одной
аркой
(t-sin t), y= (1-cos t).
циклоиды:x=
y
0
x
10.
Вычисление длины дуги кривой.11.
Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ].12.
Пусть кривая задана в параметрическойформе x=x(t), y=y(t), t
, причём x(t),
y(t), x’(t) 0, y’(t) непрерывны на
,











 mathematics
mathematics








