Similar presentations:
Тригонометрия задачки
1.
Задачки2.
3.
02
sin sin 3 ... sin(2 n 1) 0 | *sin
sin sin sin 3 sin ... sin(2 n 1) sin 0
1
1
(cos(0) cos(2 )) (cos(2 ) cos(4 )) ... 0
2
2
cos 0 cos 2 cos 2 ... cos 2n 0
cos 2n 1
2n 2 k
k
n
K max k
K
K 1
,
n
2
n
2
2018 1 2019 1
,
n
2 n
2
2* 2018 n 2* 2019
Ответ : 2* 2019, 2* 2019 1
4.
5.
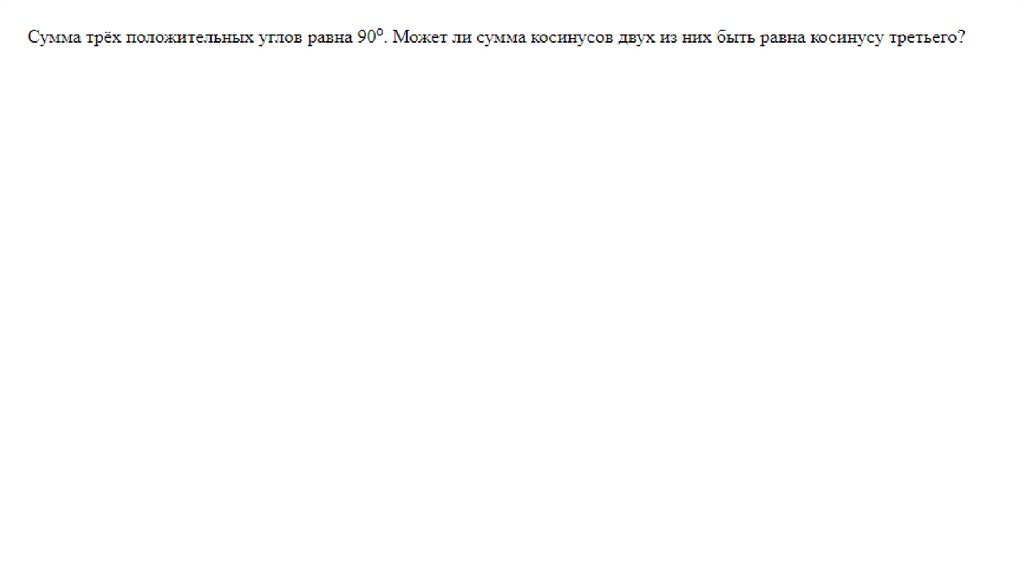
Пусть это возможно :cos(90 ) sin( ) sin cos sin cos cos cos
Равенство при :
sin sin 1
2
2
2 k , k 0
2 n, n 0
2 (n k)
Третий угол не может быть положительным противоречие
Ответ : нет
6.
7.
sin некотое числонужно найти чему равен sin
половинного угла ,
2
если известен синус этого угла :
sin sin некотое число
2 k , k
2 k , k
sin
sin
Т .е. не более 3 х значений
Пример :
0
2
sin(
2
) sin
2
2
sin(
) sin
2
2
разных значений не более 4
Пример
3
3
sin 3 t 4t 3
2 2 k, k
k, k
2
2
sin 2
sin
2
sin
2
sin
2
Итак
t sin
sin
1 1 3
3
{ , ,
, }
2
2 2 2
2
2
3
4
3
sin {0,sin( )
,sin( ) }
3
3
2
3
2
8.
9.
/2F
/2
(cos 2 (cos(x)) sin 2 (sin(x))) dx
0
/2
0
/2
cos 2 (cos(x)) dx
0
sin 2 (sin(x)) dx
0
0
sin 2 (cos( x)) dx | x y, x y | sin 2 (cos(y)) d( y)
2
2
2
2
/2
0
sin (cos(y)) d( y )
2
/2
/2
sin 2 (cos(y)) d( y)
0
/2
F
0
/2
(cos 2 (cos(x)) sin 2 (cos(x))) dx
1dx
0
2
10.
11.
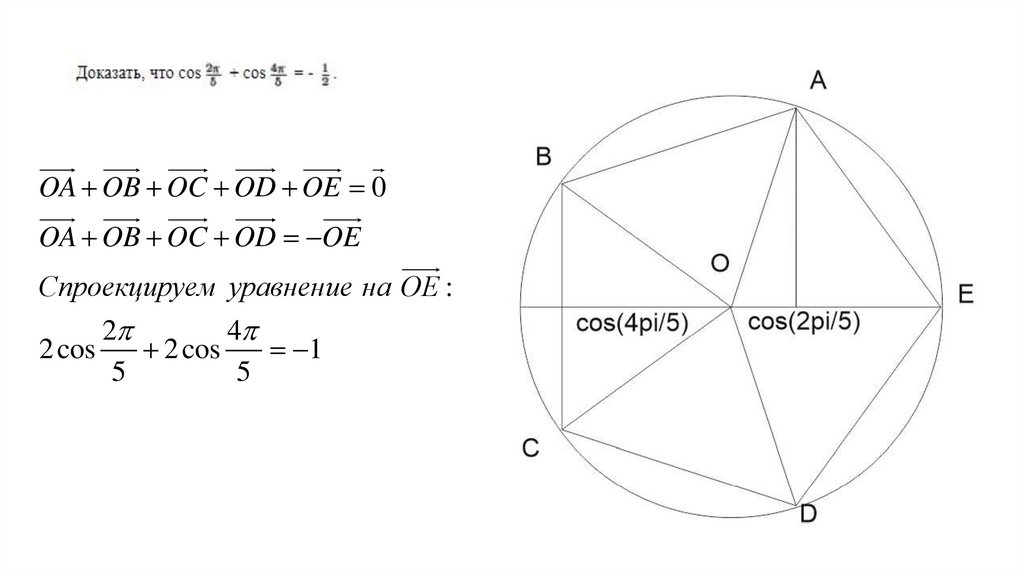
OA OB OC OD OE 0OA OB OC OD OE
Спроекцируем уравнение на OE :
2
4
2 cos
2 cos
1
5
5
12.
13.
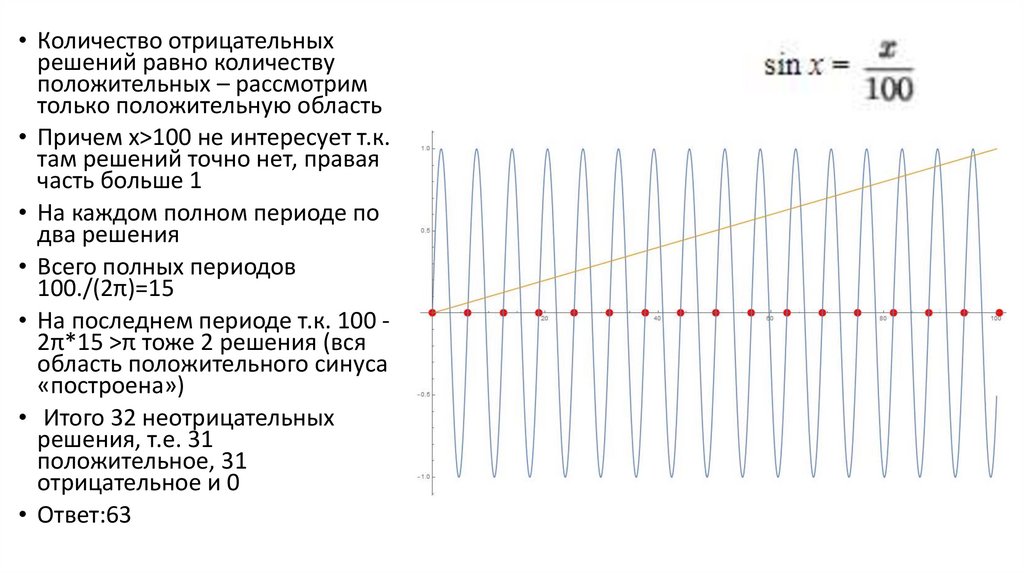
• Количество отрицательныхрешений равно количеству
положительных – рассмотрим
только положительную область
• Причем x>100 не интересует т.к.
там решений точно нет, правая
часть больше 1
• На каждом полном периоде по
два решения
• Всего полных периодов
100./(2π)=15
• На последнем периоде т.к. 100 2π*15 >π тоже 2 решения (вся
область положительного синуса
«построена»)
• Итого 32 неотрицательных
решения, т.е. 31
положительное, 31
отрицательное и 0
• Ответ:63







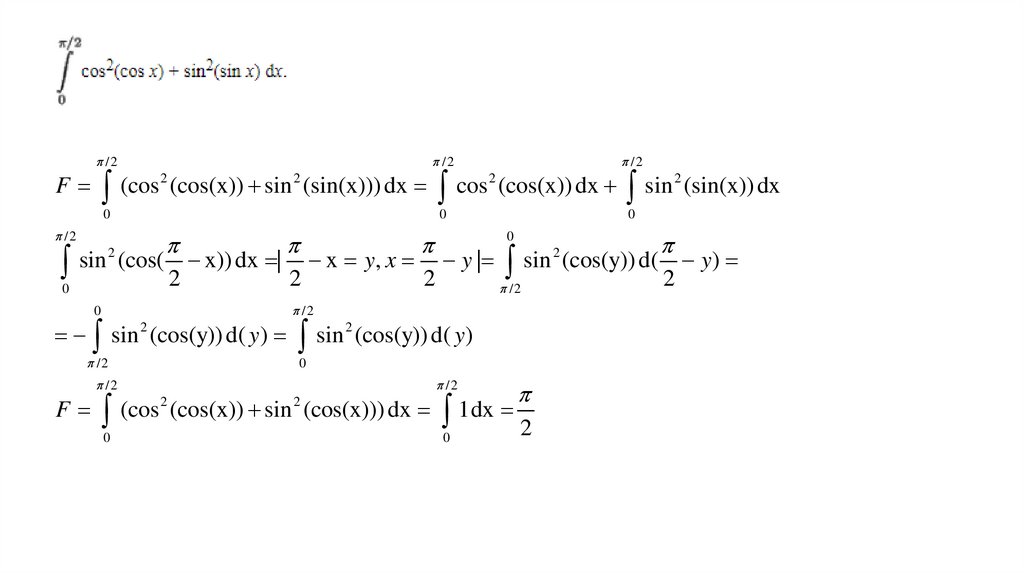


 mathematics
mathematics