Similar presentations:
Амплиту́дно-часто́тная характери́стика (АЧХ). Фа́зочасто́тная характеристика
1.
АЧХ• АЧХ
H ( ) H H
z exp( j T )
1
[1 b e
j T
] [1 b e
j T
]
1
1 b 2b cos T
2
(4)
2.
ФЧХ• ФЧХ
( ) arg H ( z ) z exp( j T )
Im H ( z )
arctg
z exp( j T )
Re H ( z )
b sin T
arctg
1 b cos T
(5)
3.
АЧХИз (4) следует, что
при b > 0 имеем фильтр нижних частот, а
при b < 0 – фильтр верхних частот.
При b > 0 из (4) находим, что АЧХ имеет
максимальное значение Hmax на частоте f =0, а
минимальное значение Hmin – на частоте f = fs /2
(т.е. при T = /2):
H max
1
H ( 0)
1 b
(6),
H min
1
H ( f s / 2)
1 b
(7).
4.
АЧХ и АЧХ• Для определенных областей изменения аргумента
T
получаем еще более простые формулы :
K ( )
1
1 ( T / ) 2
K ( )
,
2 sin( T / 2)
,
, ( T ) 2 1
(12),
1, T (3 4)
(13),
T
( ) arctg
,
T 1
(14).
5.
Полоса пропускания• Формулы (12) и (14) описывают поведение АЧХ и ФЧХ
РЦФ 1-порядка в полосе пропускания, а формула (13)
– поведение АЧХ в полосе задерживания.
• Обычно ширину полосы пропускания f ФНЧ
определяют из условия
2
(15).
K ( f )
2
• Сравнивая (12) и (15), получаем 2 f T = , откуда
имеем:
fs
f
,
2
1
(16).
6.
Расчет коэффициента b• Если заданы частота дискретизации и полоса
фильтра, то значение его коэффициента b
(или = 1 – b) можно определить по формулам
2 f
b 1
fs
(17),
2 f
fs
(18).
7.
Групповое время задержкиВажным параметром является так называемое
групповое время задержки (ГВЗ) ( ), которое
определяется как производная от фазы по частоте:
( )=d d .
• Для ГВЗ получим следующую формулу:
b cos T
( ) bT
2
1 b 2b cos T
(19).
8.
Групповое время задержки• Обычно ГВЗ имеет смысл рассматривать лишь в
полосе пропускания фильтра. Для этого случая
формулу (19) можно существенно упростить:
( ) T 2
,
2
( T )
T 1
(0) T/ , а на краю полосы
пропускания ( f) T/2 .
• На нулевой частоте
(20).
9.
Время задержки импульса• Время задержки
з импульса определим из условия
достижения выходным сигналом фильтра уровня,
равного половине установившегося значения:
• y( з) = 0,5 y .
• При << 1 из (23) получим
• nз 0,7 / ,
• откуда для времени задержки имеем
з
0,7
T
(24).
10.
Время нарастания• Время нарастания
н переходной характеристики
определим из условия
• н = (n0,9 – n0,1) T ,
• где n0,9 и n0,1 - количество периодов частоты
дискретизации, за которое переходная характеристика
достигает, соответственно, уровня 0,9 и 0,1 от
установившегося значения y .
• При << 1 из (23) получим
н
2,2
T
(25).
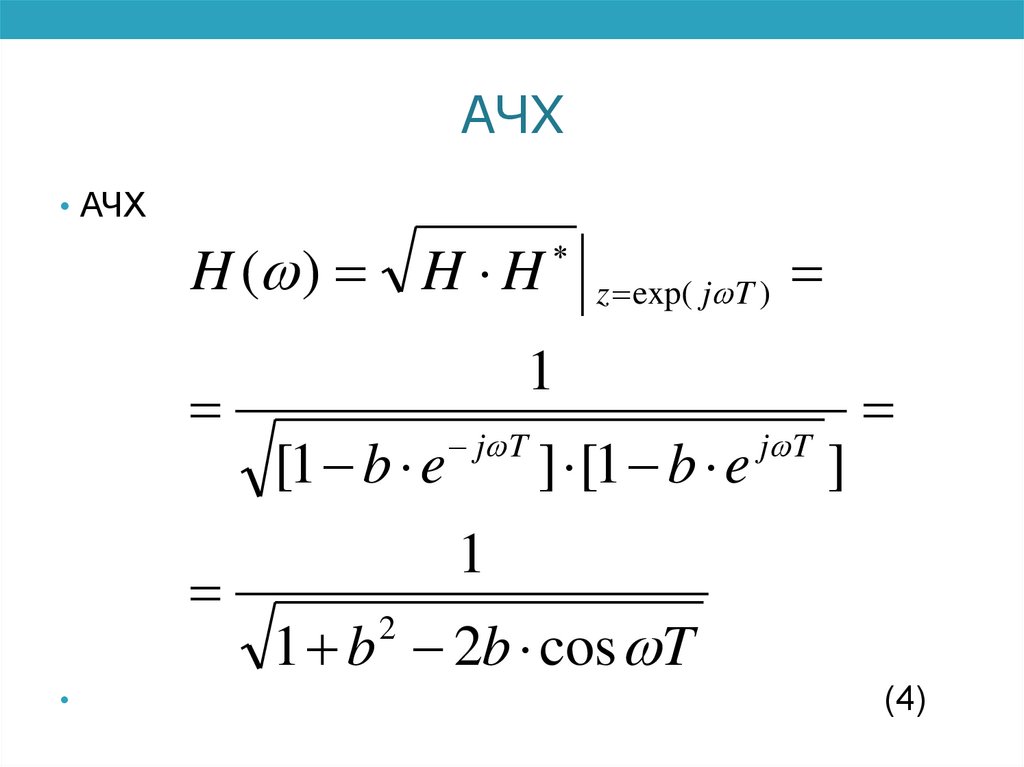
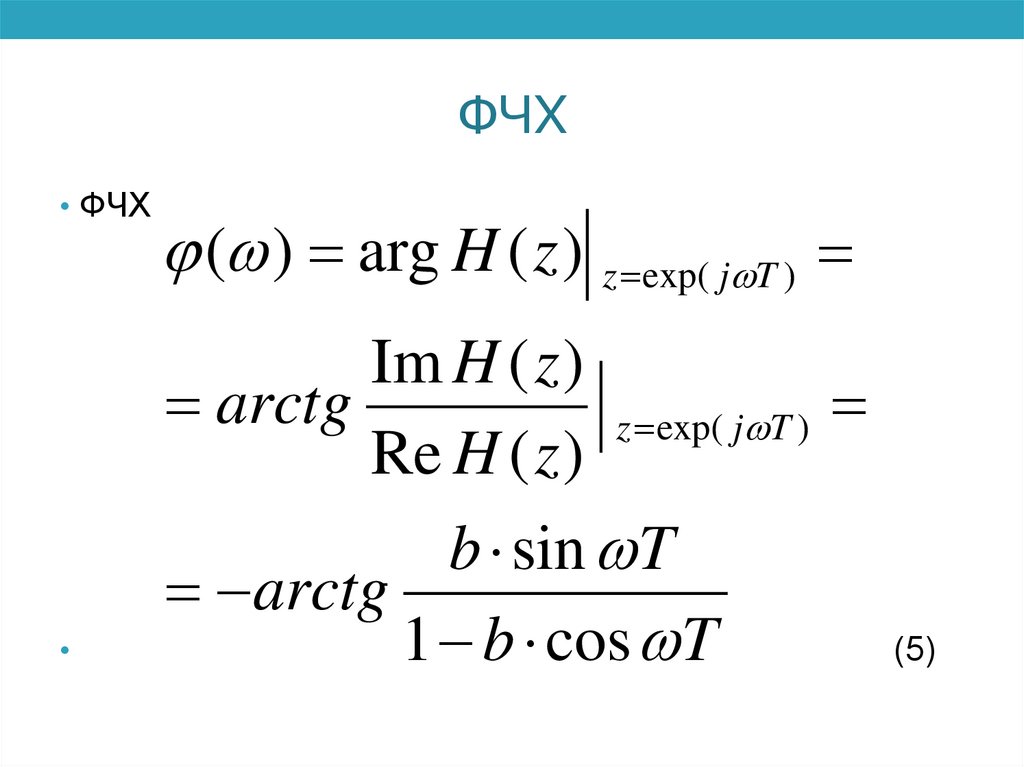








 physics
physics electronics
electronics








