Кривые Безье

1. Кривые Безье

Координаты кривой описываются в зависимости от
параметра t є [0,1]
Bi – функция компонент опорных вершин
(координаты опорных точек по x и у)
Параметрическое представление кривой Безье:
,
,
где базис Безье-Бернштейна, или функция аппроксимации
, где
- базисные функции кривой Безье , i-я функция базиса Бернштейна порядка n.

2. Кривые Безье

Координаты кривой описываются в зависимости от
параметра t є [0,1]
Для двух точек:
P = (1-t)B0 + tB1
• Для трёх точек:
P = (1−t)2B0 + 2(1−t)tB1 + t2B2
• Для четырёх точек:
P = (1−t)3B0 + 3(1−t)2tB1 +3(1−t)t2B2 + t3B3

3. https://www.kontrolnaya-rabota.ru/s/grafik/tochka/

https://www.kontrolnayarabota.ru/s/grafik/tochka/
3

4. Задание

4
Задание
Кривые высших степеней
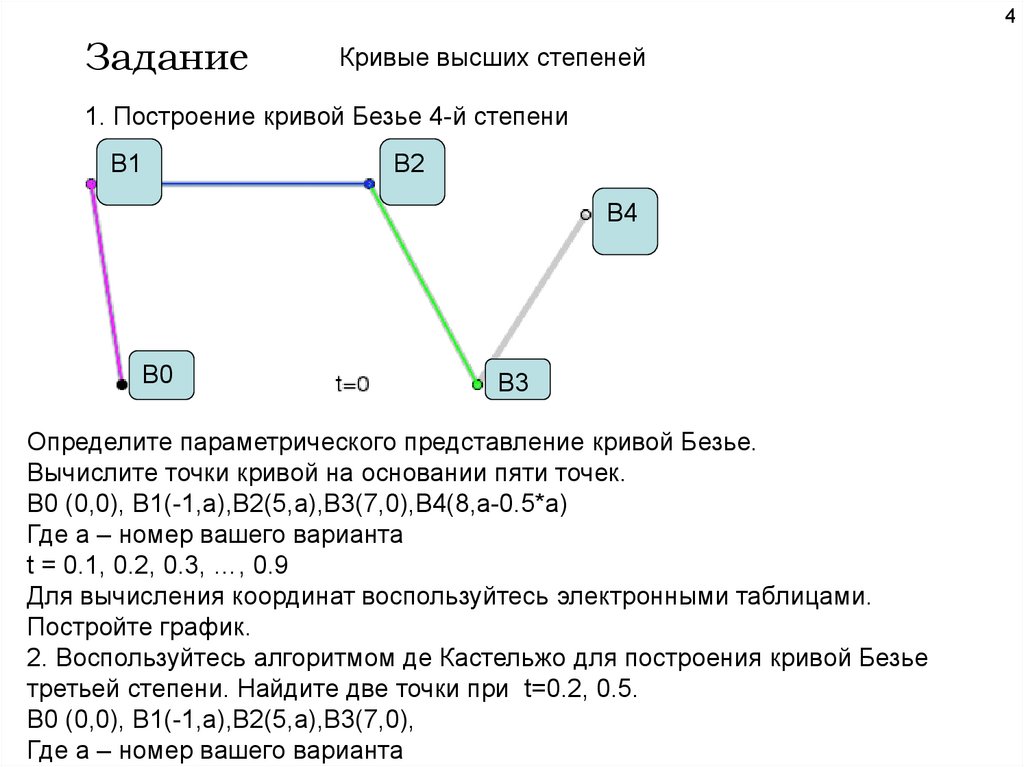
1. Построение кривой Безье 4-й степени
В1
В2
В4
В0
В3
Определите параметрического представление кривой Безье.
Вычислите точки кривой на основании пяти точек.
B0 (0,0), B1(-1,a),B2(5,a),B3(7,0),B4(8,a-0.5*a)
Где а – номер вашего варианта
t = 0.1, 0.2, 0.3, …, 0.9
Для вычисления координат воспользуйтесь электронными таблицами.
Постройте график.
2. Воспользуйтесь алгоритмом де Кастельжо для построения кривой Безье
третьей степени. Найдите две точки при t=0.2, 0.5.
B0 (0,0), B1(-1,a),B2(5,a),B3(7,0),
Где а – номер вашего варианта