Кривые на плоскости

1. Кривые на плоскости

Лекция 3

2. Задача построения произвольных кривых

Линия может быть задана в форме
неявного уравнения или в
параметрической форме
Задача в этом случае сводится к
нахождению соответствующих
функциональных зависимостей

3. Задача построения произвольных кривых

Задача построения
произвольных
Однако на практике линия обычно
кривых
задается некоторым множеством точек и
задача ее построения может быть
сформулирована одним из двух способов:
как задача интерполяции
как задача аппроксимации

4. Задача интерполяции

На заданном классе функций (например,
полиномов указанной степени) ищется
функция, обеспечивающая прохождение
описываемой ею кривой через заданное
множество точек

5. Сплайны

В этом случае широко применяется
подход, основанный на использовании
полиномов невысокой степени,
называемых сплайнами
Основная идея заключается в том, чтобы
не пытаться найти функциональные
зависимости, которые описывали бы
линию в целом

6. Сплайновое приближение

Вместо этого воспроизводится достаточно
точное описание отдельных участков этой
линии с обеспечением плавного перехода
между такими участками
Подобное кусочно-гладкое описание
кривой, заданной конечным множеством
своих точек, называется ее сплайновым
приближением

7. Интерполяционные полиномы Лагранжа

Пусть на плоскости задан набор точек (xi, yi), i
= 0,1,…,n
Кривая, проходящая через каждую из этих
точек, описывается полиномом n-й степени многочленом Лагранжа, который имеет вид:
Ln ( x) i 0 yi
n
j i
x xj
xi x j

8. Недостатки многочлена Лагранжа

Недостатки
многочлена
Многочлен Лагранжа описывает кривую в
Лагранжа
целом, однако такое описание имеет ряд
недостатков:
высокая степень полинома приводит к
сильным колебаниям интерполирующей
функции между узлами интерполяции
интерполирующая функция обладает высокой
чувствительностью к узловым значениям
изменение одного из узлов приводит к
необходимости пересчета всей функции

9. Кубические сплайны

Вместо интерполяционных полиномов
Лагранжа используют кубические сплайны
Кубическим сплайном называется функция
S(x), обладающая следующими
свойствами:
описываемая ею кривая проходит через
каждую точку заданного множества, т.е. S(x i)=yi
на каждом из отрезков [xi, xi+1] функция является
многочленом 3-й степени
на всем отрезке [x0, xn] функция имеет
непрерывную вторую производную

10. Кубические сплайны

Таким образом, задача сводится к
построению n полиномов вида:
y = ai3 * x3 + ai2 * x2 + ai1 * x + ai0, i=1, 2,…,n
Соответственно, потребуется найти 4n
коэффициентов aij (i=1,…,n; j=0,1,2,3) этих
полиномов

11. Кубические сплайны

Коэффициенты полиномов определяются
системой линейных уравнений, которые
получаются из следующих условий:
прохождения через каждый из узлов (n+1
условие),
непрерывности функции в промежуточных
узлах (n-1 условие),
непрерывности 1-й производной функции в
промежуточных узлах (n-1 условие),
непрерывности 2-й производной функции в n-1
промежуточных узлах (n-1 условие),

12. Кубические сплайны

2-х дополнительных условий в граничных узлах
(например, равенства нулю первых
производных)
Тем самым, удается получить систему 4n
линейных уравнений с 4n неизвестными,
имеющую при ненулевом детерминанте
единственное решение

13. Задача аппроксимации

Задача заключается в построении гладкой
кривой, наилучшим образом
приближенной к некоторому множеству
точек в пространстве или на плоскости

14. Методы аппроксимации

Наиболее известные методы
аппроксимации:
метод наименьших квадратов
метод кривых Безье
метод B-сплайнов.

15. Метод наименьших квадратов

На заданном классе функций (например,
полиномов указанной степени) ищется
функция, обеспечивающая минимальное
значение суммы квадратов отклонений на
некотором множестве точек

16. Аппроксимация полиномом

17. Аппроксимация полиномом

18. Аппроксимация полиномом

19. Кривые Безье

Пусть в пространстве или на плоскости
задан упорядоченный набор точек,
определяемый векторами V0, V1, … , Vm.
Ломаная V0V1 …Vm называется
контрольной ломаной, порожденной
массивом V ={ V0, V1, … , Vm }.

20. Кривые Безье

Кривой Безье, определяемой массивом V,
называется линия задаваемая векторным
уравнением
m
r (t ) Cmi t i (1 t ) m i V i , 0 t 1,
i 0
где
m!
C
i!(m i )!
i
m
- биномиальные коэффициенты.

21. Свойства кривых Безье

Гладкость
Линия начинается в точке и заканчивается в
точке касаясь при этом отрезков и
контрольной ломаной
Коэффициенты при вершинах Vi являются
многочленами Бернштейна; они
неотрицательны и их сумма равна 1.
m
i i
m i
m
C
t
(
1
t
)
(
t
(
1
t
))
1
m
i 0

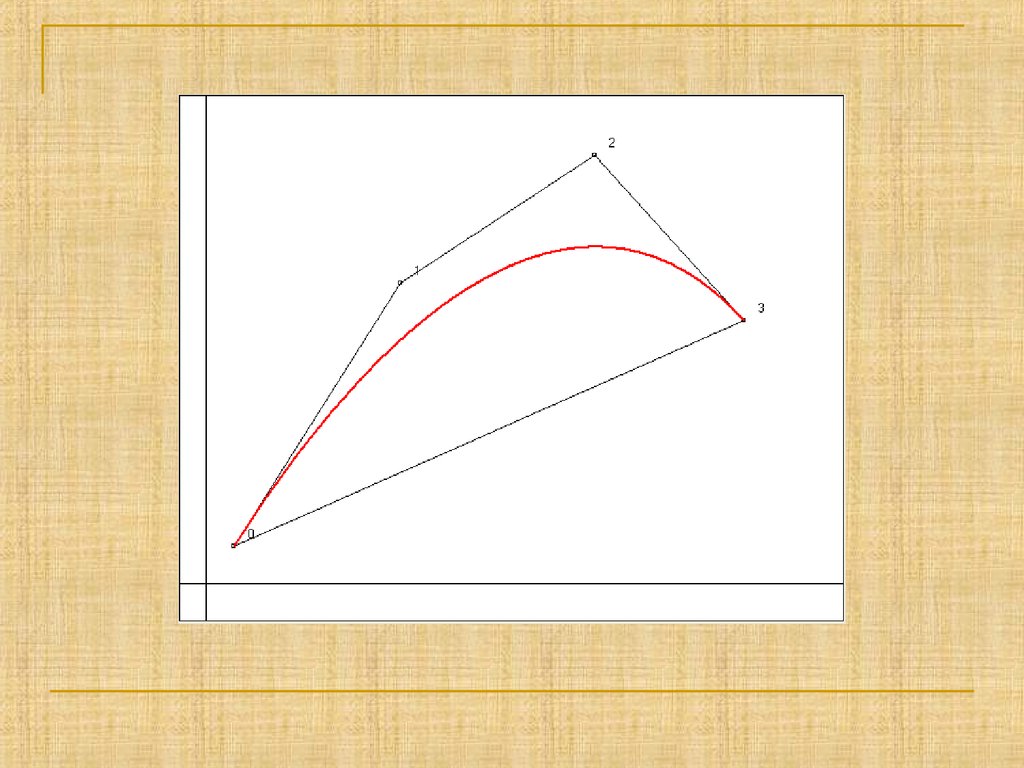
22. Кубическая кривая Безье

При m = 3 получаем кубическую кривую
Безье, описываемую векторным
параметрическим уравнением
r (t ) V0 (1 t ) 3V1t (1 t ) 3V2t (1 t ) V3t
3
2
2
3
Порядок точек в заданном наборе
существенно влияет на вид кривой Безье.
что демонстрируется на следующих
слайдах.

23.

24.

25.

26.

27. Недостатки кривых Безье

Степень функциональных коэффициентов
связана с числом точек в заданном наборе
При добавлении хотя бы одной точки в
набор все коэффициенты должны быть
пересчитаны
Изменение хотя бы одной точки приводит к
заметному изменению вида всей кривой.

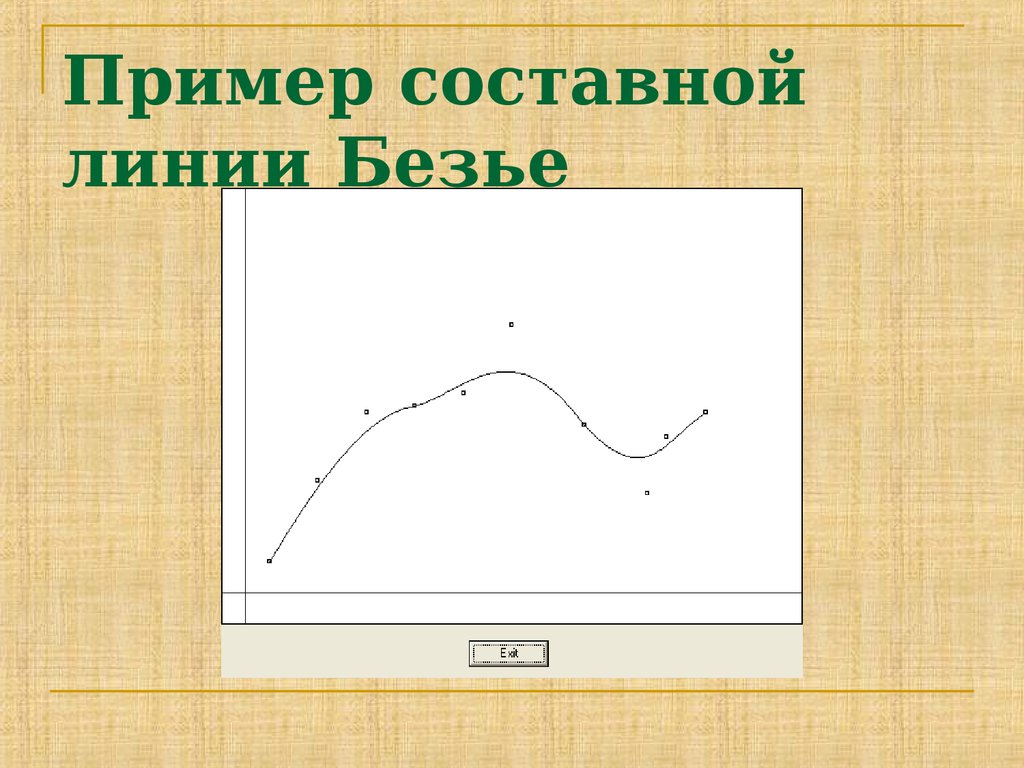
28. Составная кубическая кривая Безье

В практических вычислениях оказывается
удобным пользоваться кривыми,
составленными из элементарных кривых
Безье, как правило кубических. При этом
обеспечить гладкость в точках стыковки.
Составная кривая называется G1–
непрерывной, если вдоль нее непрерывен
единичный вектор касательной и G2–
непрерывной, если непрерывен также и
вектор кривизны.

29. Пример составной линии Безье