Similar presentations:
Пересечение поверхностей. Часть 2
1. Модуль «Начертательная геометрия» Тема 6 (тетрадь «6 тем»)
2.
содержание лекцииметоды построения линии пересечения
двух поверхностей (Часть 2)
метод сфер-посредников
(способ вспомогательных секущих сфер)
основные термины
способ концентрических сфер
частный случай пересечения поверхностей
(теорема Монжа)
способ эксцентрических сфер
примеры решений задач из методички [2]
литература
3.
задачи4.
содержание лекцииметоды построения линии пересечения
двух поверхностей (Часть 2)
метод сфер-посредников
(способ вспомогательных секущих сфер)
основные термины
способ концентрических сфер
частный случай пересечения поверхностей
(теорема Монжа)
способ эксцентрических сфер
примеры решений задач из методички [2]
литература
5.
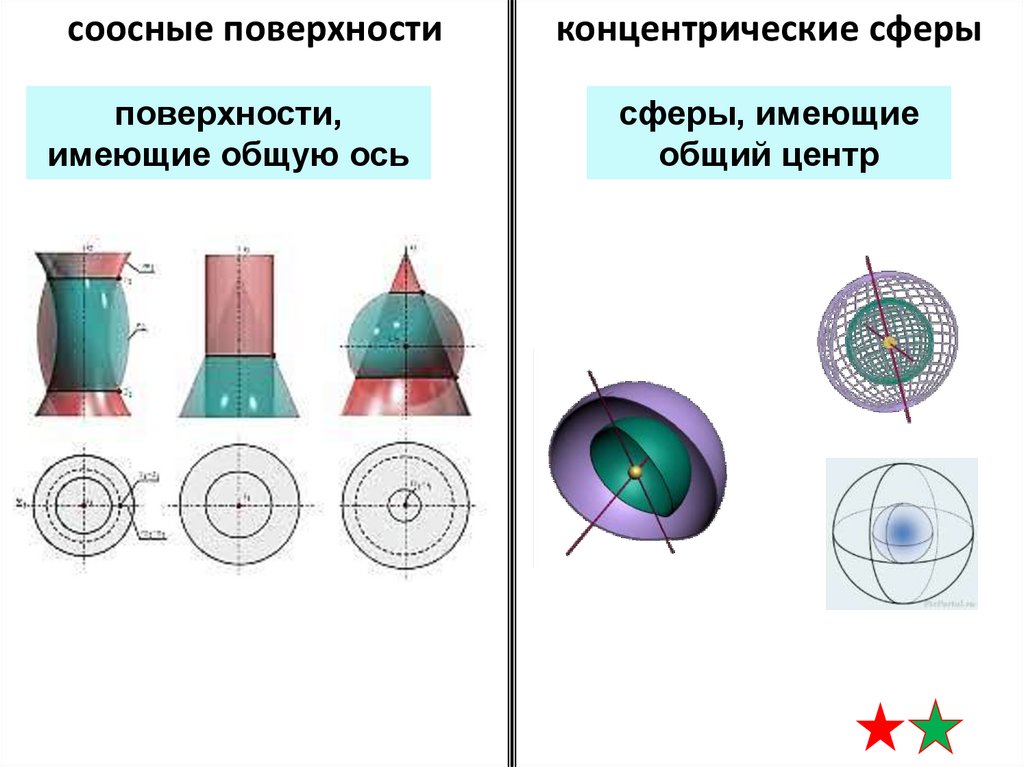
соосные поверхностиповерхности,
имеющие общую ось
концентрические сферы
сферы, имеющие
общий центр
6.
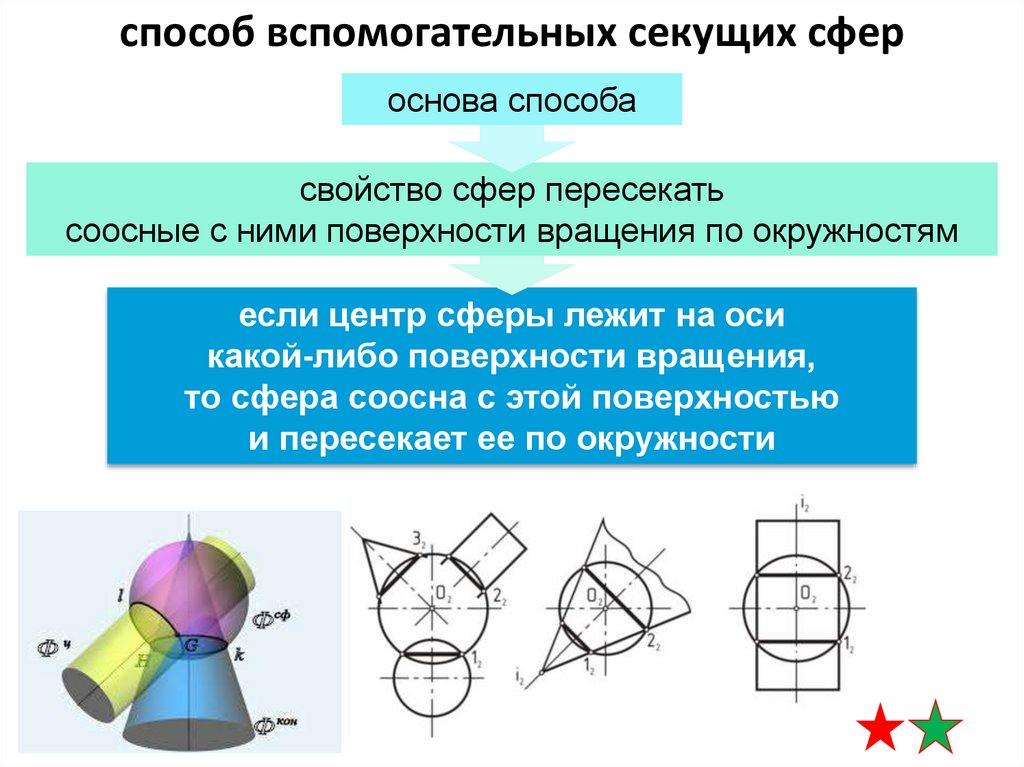
способ вспомогательных секущих сфероснова способа
свойство сфер пересекать
соосные с ними поверхности вращения по окружностям
если центр сферы лежит на оси
какой-либо поверхности вращения,
то сфера соосна с этой поверхностью
и пересекает ее по окружности
7.
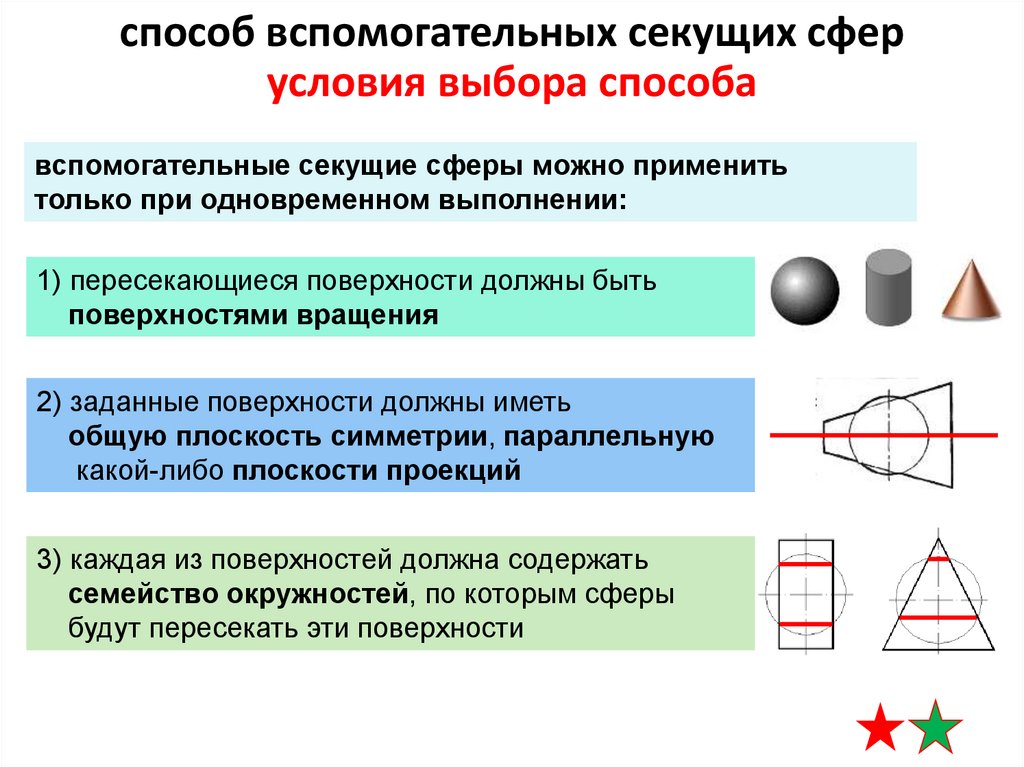
способ вспомогательных секущих сферусловия выбора способа
вспомогательные секущие сферы можно применить
только при одновременном выполнении:
1) пересекающиеся поверхности должны быть
поверхностями вращения
2) заданные поверхности должны иметь
общую плоскость симметрии, параллельную
какой-либо плоскости проекций
3) каждая из поверхностей должна содержать
семейство окружностей, по которым сферы
будут пересекать эти поверхности
8.
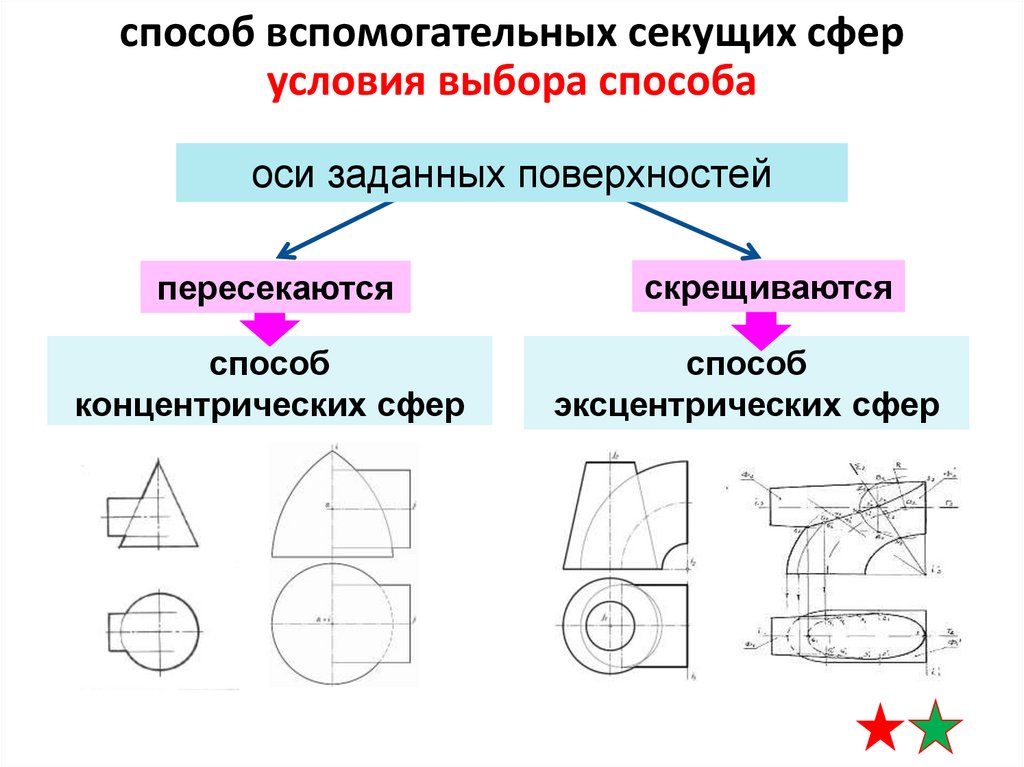
способ вспомогательных секущих сферусловия выбора способа
оси заданных поверхностей
пересекаются
способ
концентрических сфер
скрещиваются
способ
эксцентрических сфер
9.
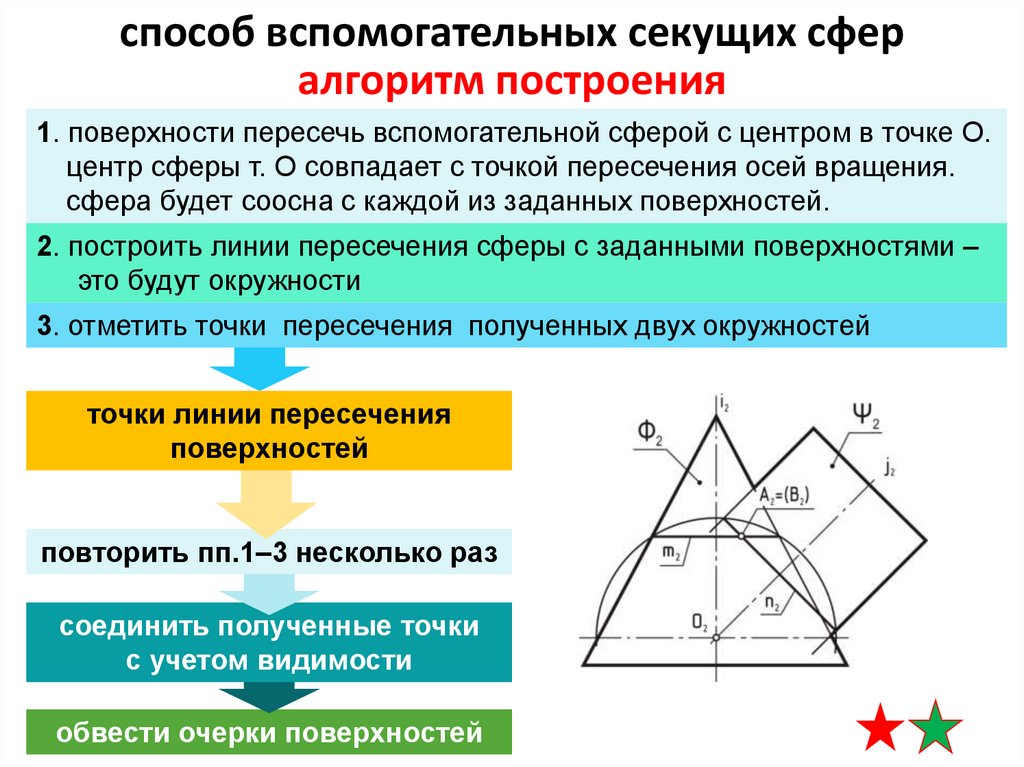
способ вспомогательных секущих сфералгоритм построения
1. поверхности пересечь вспомогательной сферой с центром в точке О.
центр сферы т. О совпадает с точкой пересечения осей вращения.
сфера будет соосна с каждой из заданных поверхностей.
2. построить линии пересечения сферы с заданными поверхностями –
это будут окружности
3. отметить точки пересечения полученных двух окружностей
точки линии пересечения
поверхностей
повторить пп.1–3 несколько раз
соединить полученные точки
с учетом видимости
обвести очерки поверхностей
10.
содержание лекцииметоды построения линии пересечения
двух поверхностей (Часть 2)
метод сфер-посредников
(способ вспомогательных секущих сфер)
основные термины (соосные, концентрические)
способ концентрических сфер
частный случай пересечения поверхностей
(теорема Монжа)
способ эксцентрических сфер
примеры решений задач из методички [2]
литература
11.
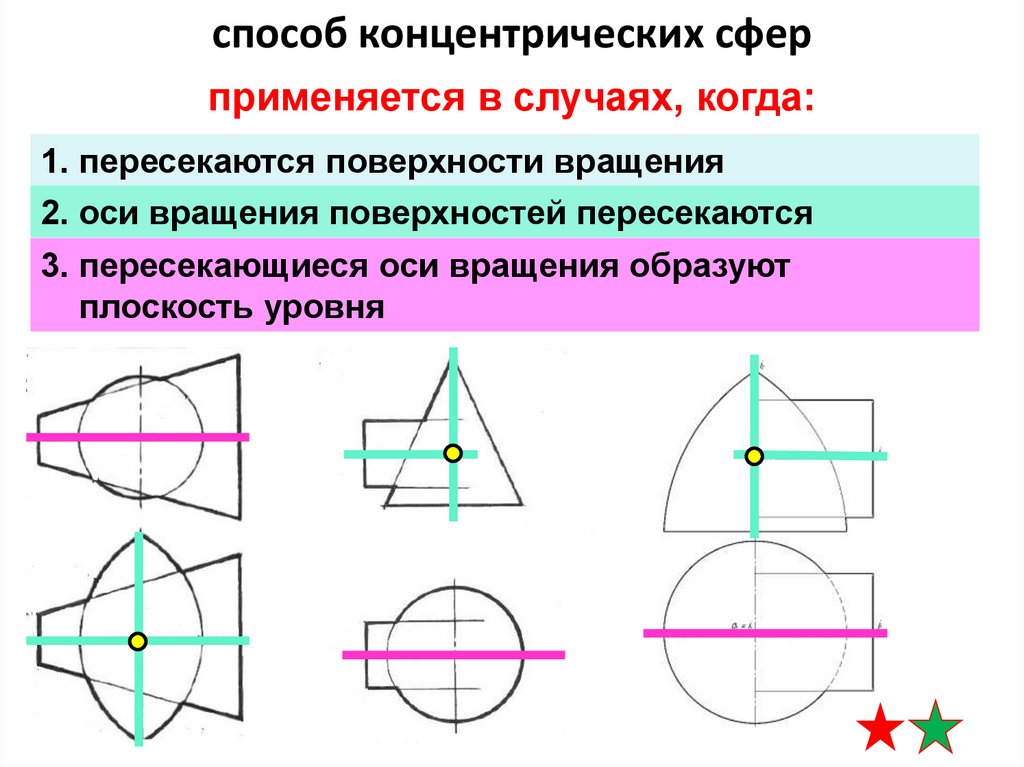
способ концентрических сферприменяется в случаях, когда:
1. пересекаются поверхности вращения
2. оси вращения поверхностей пересекаются
3. пересекающиеся оси вращения образуют
плоскость уровня
12.
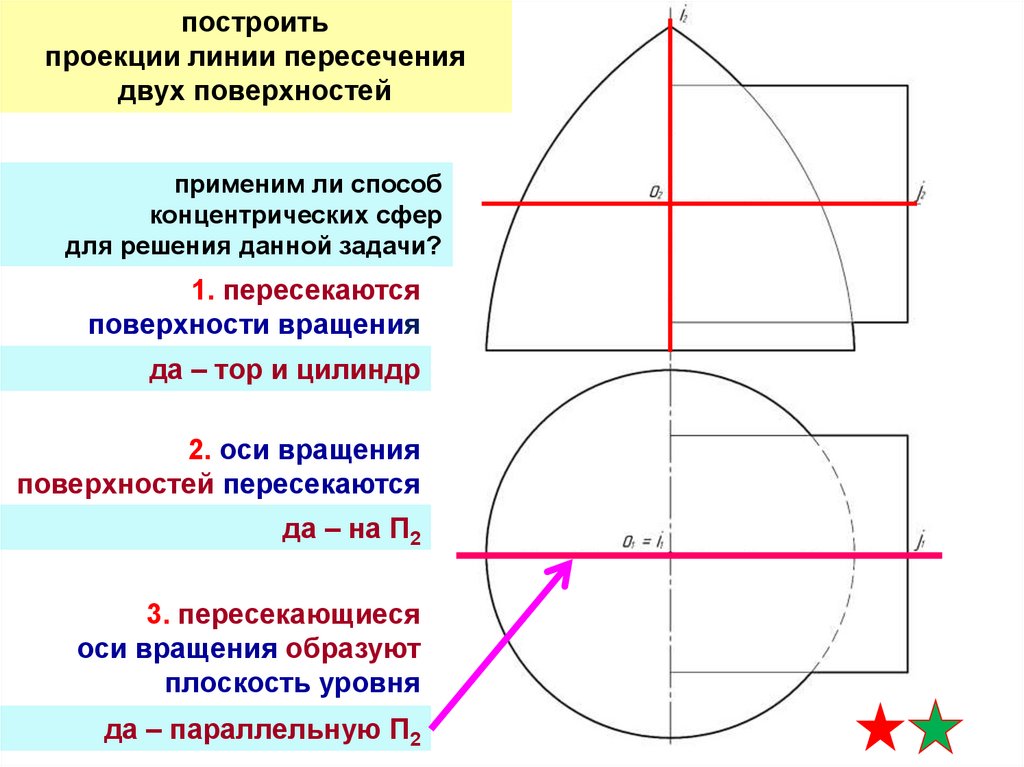
построитьпроекции линии пересечения
двух поверхностей
применим ли способ
концентрических сфер
для решения данной задачи?
1. пересекаются
поверхности вращения
да – тор и цилиндр
2. оси вращения
поверхностей пересекаются
да – на П2
3. пересекающиеся
оси вращения образуют
плоскость уровня
да – параллельную П2
13.
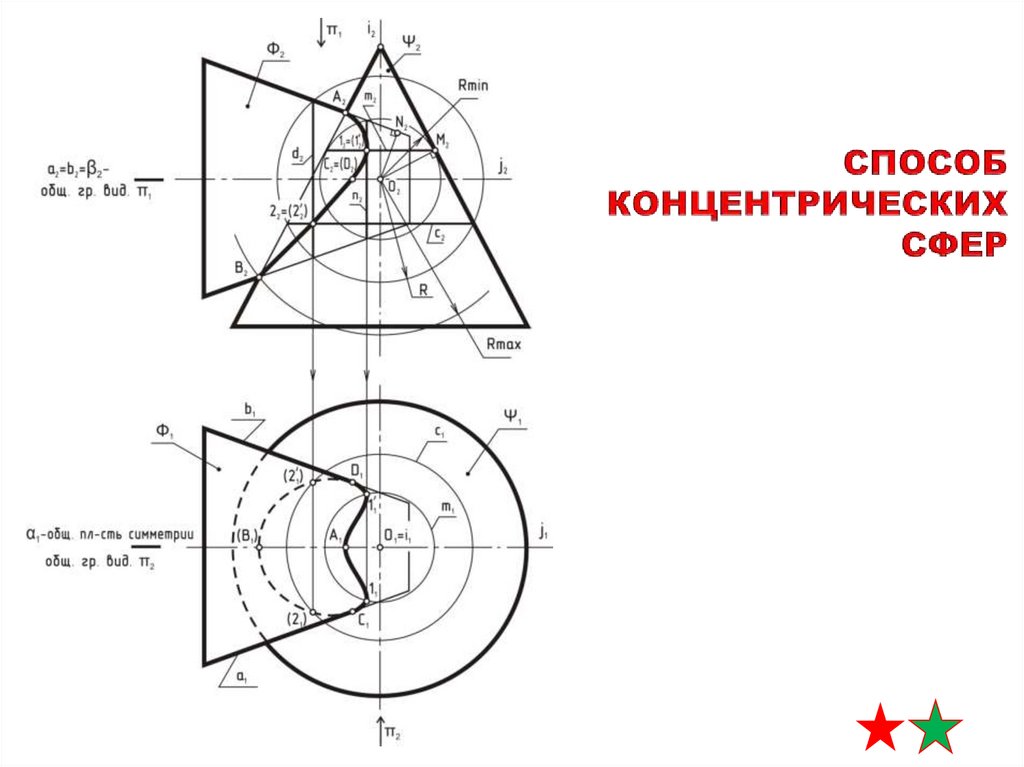
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
A2
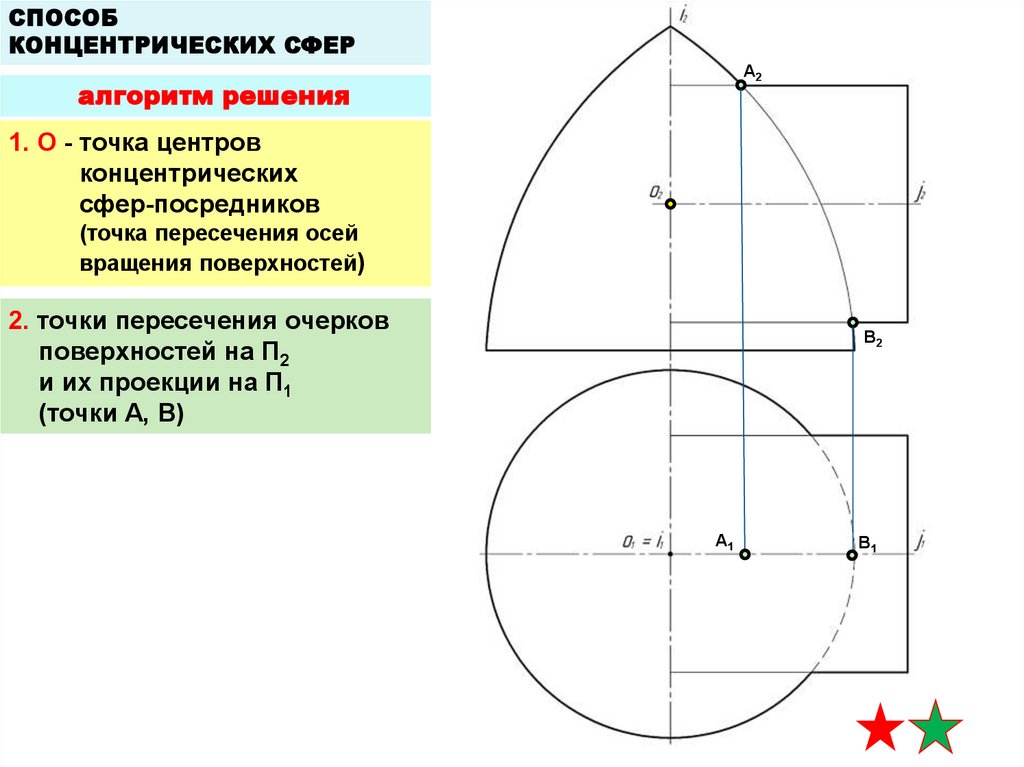
алгоритм решения
1. О - точка центров
концентрических
сфер-посредников
(точка пересечения осей
вращения поверхностей)
2. точки пересечения очерков
поверхностей на П2
и их проекции на П1
(точки A, B)
B2
A1
B1
14.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
Rmin
A2
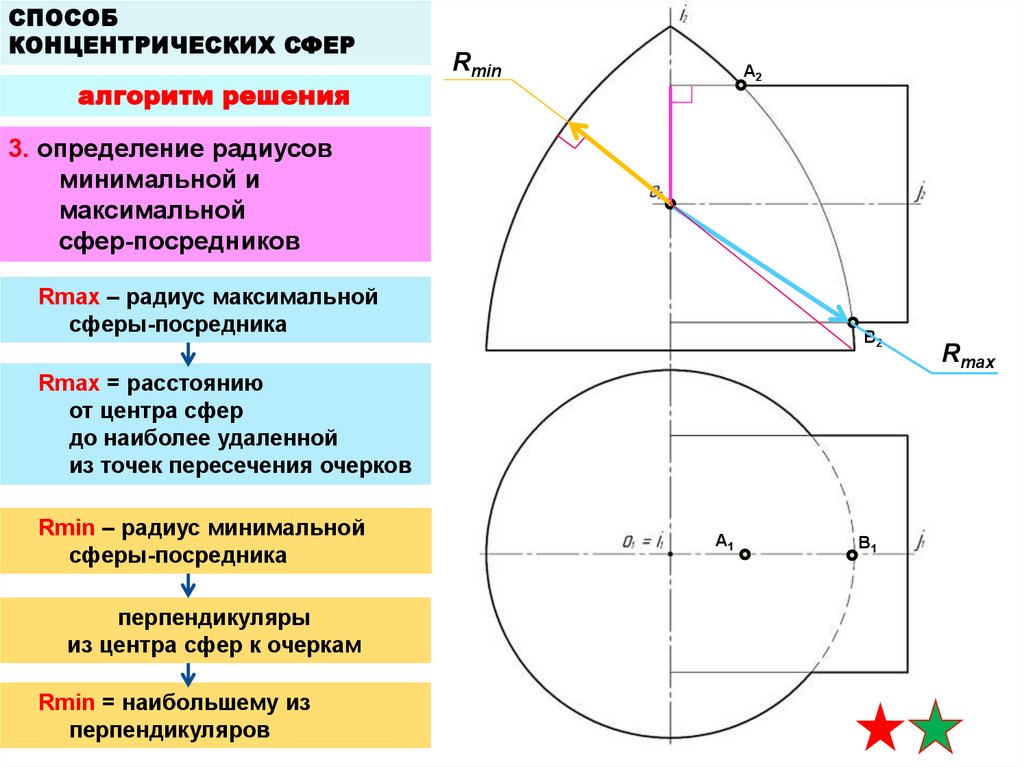
3. определение радиусов
минимальной и
максимальной
сфер-посредников
Rmax – радиус максимальной
сферы-посредника
B2
Rmax = расстоянию
от центра сфер
до наиболее удаленной
из точек пересечения очерков
Rmin – радиус минимальной
сферы-посредника
перпендикуляры
из центра сфер к очеркам
Rmin = наибольшему из
перпендикуляров
A1
B1
Rmax
15.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
Rmin
A2
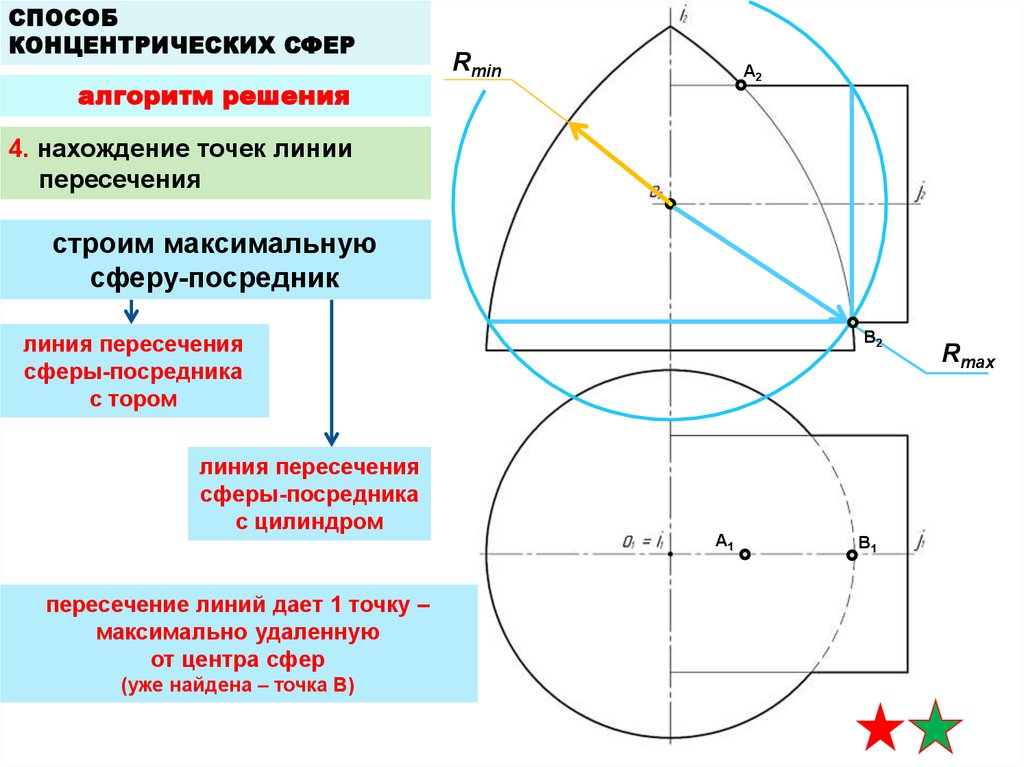
4. нахождение точек линии
пересечения
строим максимальную
сферу-посредник
B2
линия пересечения
сферы-посредника
с тором
линия пересечения
сферы-посредника
с цилиндром
A1
пересечение линий дает 1 точку –
максимально удаленную
от центра сфер
(уже найдена – точка B)
B1
Rmax
16.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
Rmin
A2
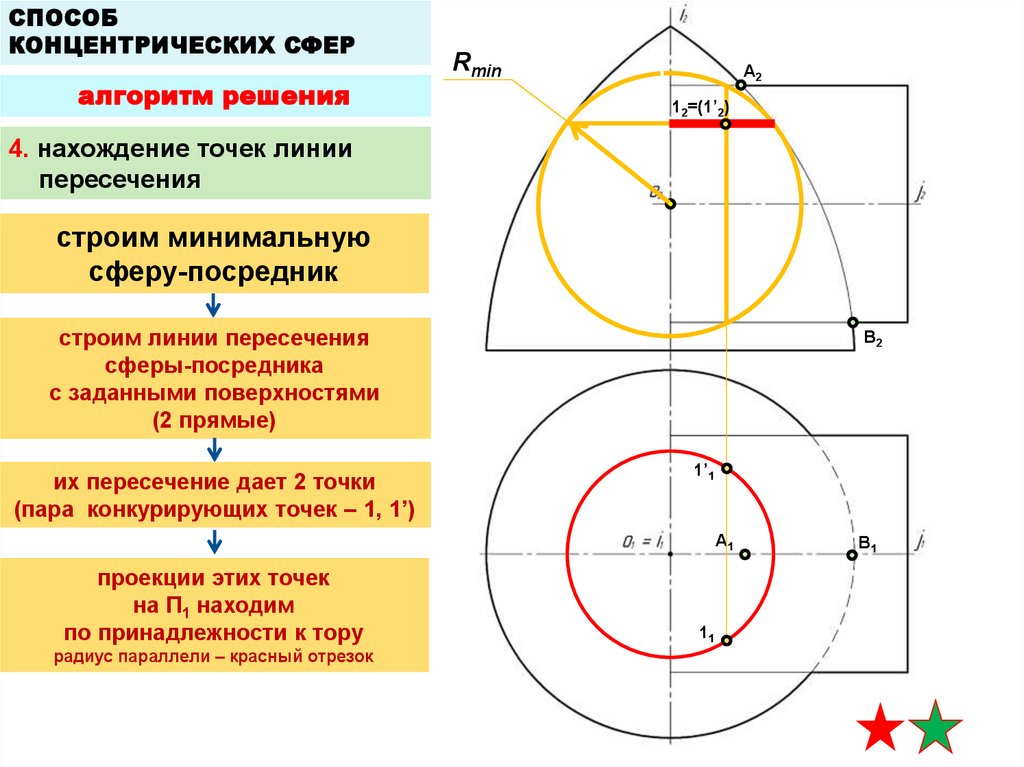
12=(1’2)
4. нахождение точек линии
пересечения
строим минимальную
сферу-посредник
строим линии пересечения
сферы-посредника
с заданными поверхностями
(2 прямые)
их пересечение дает 2 точки
(пара конкурирующих точек – 1, 1’)
B2
1’1
A1
проекции этих точек
на П1 находим
по принадлежности к тору
радиус параллели – красный отрезок
11
B1
17.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
Rmin
A2
12=(1’2)
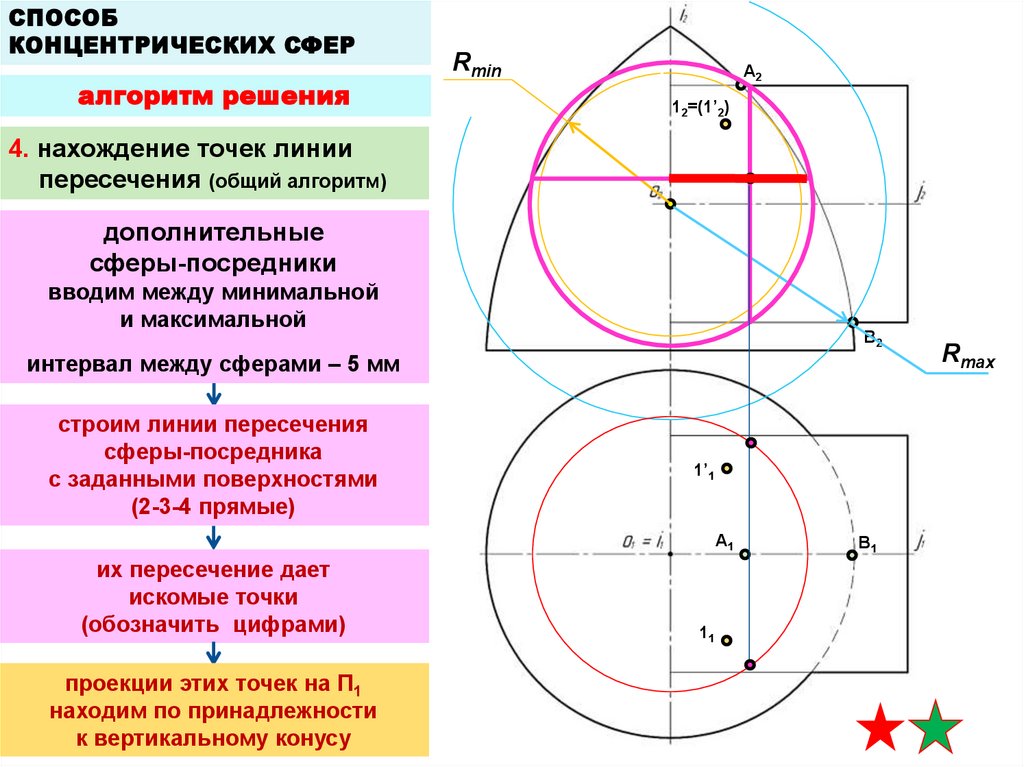
4. нахождение точек линии
пересечения (общий алгоритм)
дополнительные
сферы-посредники
вводим между минимальной
и максимальной
B2
интервал между сферами – 5 мм
строим линии пересечения
сферы-посредника
с заданными поверхностями
(2-3-4 прямые)
1’1
A1
их пересечение дает
искомые точки
(обозначить цифрами)
проекции этих точек на П1
находим по принадлежности
к вертикальному конусу
11
B1
Rmax
18.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
Rmin
A2
12=(1’2)
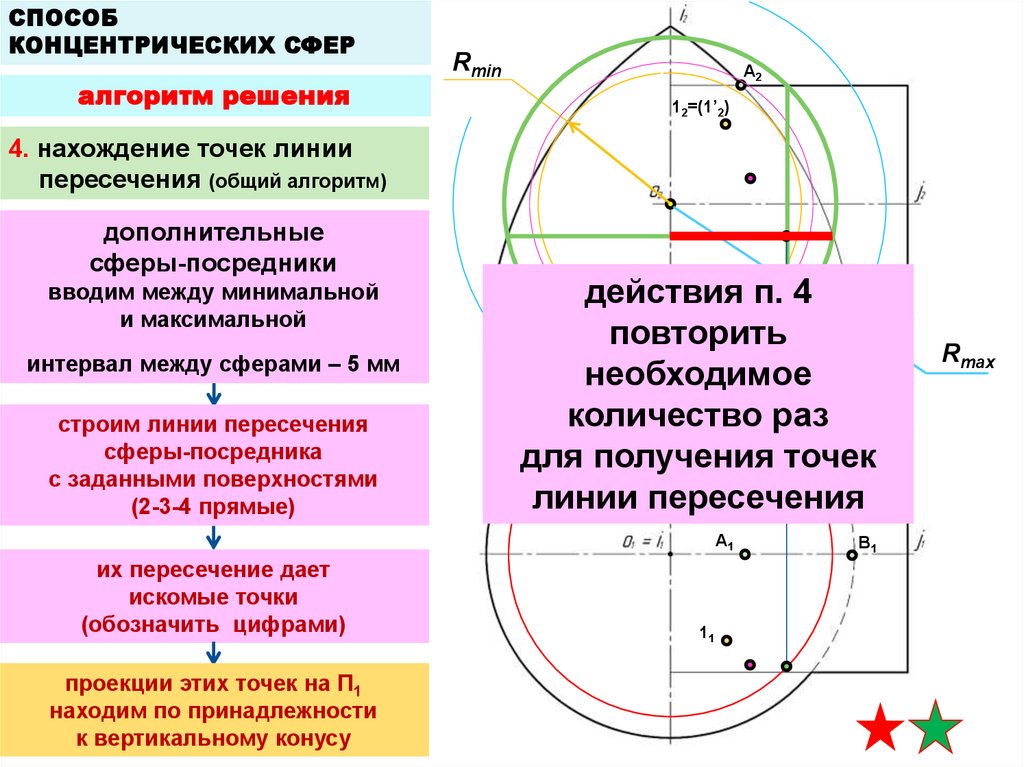
4. нахождение точек линии
пересечения (общий алгоритм)
дополнительные
сферы-посредники
вводим между минимальной
и максимальной
действия п. 4
B
повторить
необходимое
количество раз
для получения
точек
1’
линии пересечения
2
интервал между сферами – 5 мм
строим линии пересечения
сферы-посредника
с заданными поверхностями
(2-3-4 прямые)
1
A1
их пересечение дает
искомые точки
(обозначить цифрами)
проекции этих точек на П1
находим по принадлежности
к вертикальному конусу
11
B1
Rmax
19.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
Rmin
A2
12=(1’2)
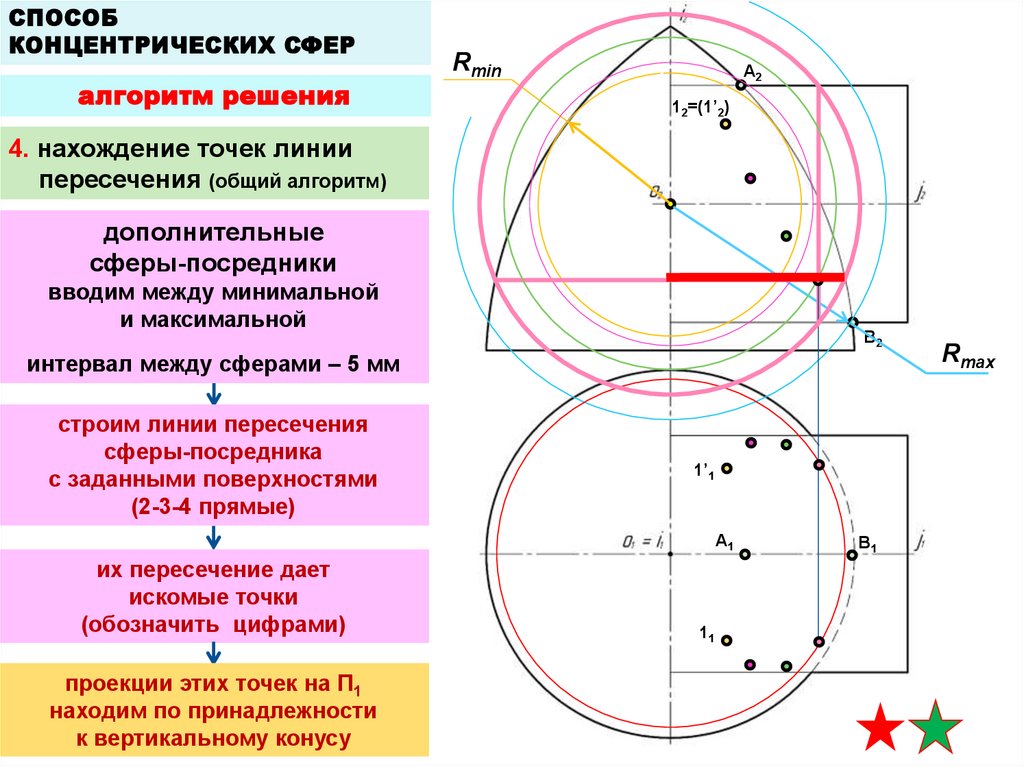
4. нахождение точек линии
пересечения (общий алгоритм)
дополнительные
сферы-посредники
вводим между минимальной
и максимальной
B2
интервал между сферами – 5 мм
строим линии пересечения
сферы-посредника
с заданными поверхностями
(2-3-4 прямые)
1’1
A1
их пересечение дает
искомые точки
(обозначить цифрами)
проекции этих точек на П1
находим по принадлежности
к вертикальному конусу
11
B1
Rmax
20.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
A2
12=(1’2)
на п1
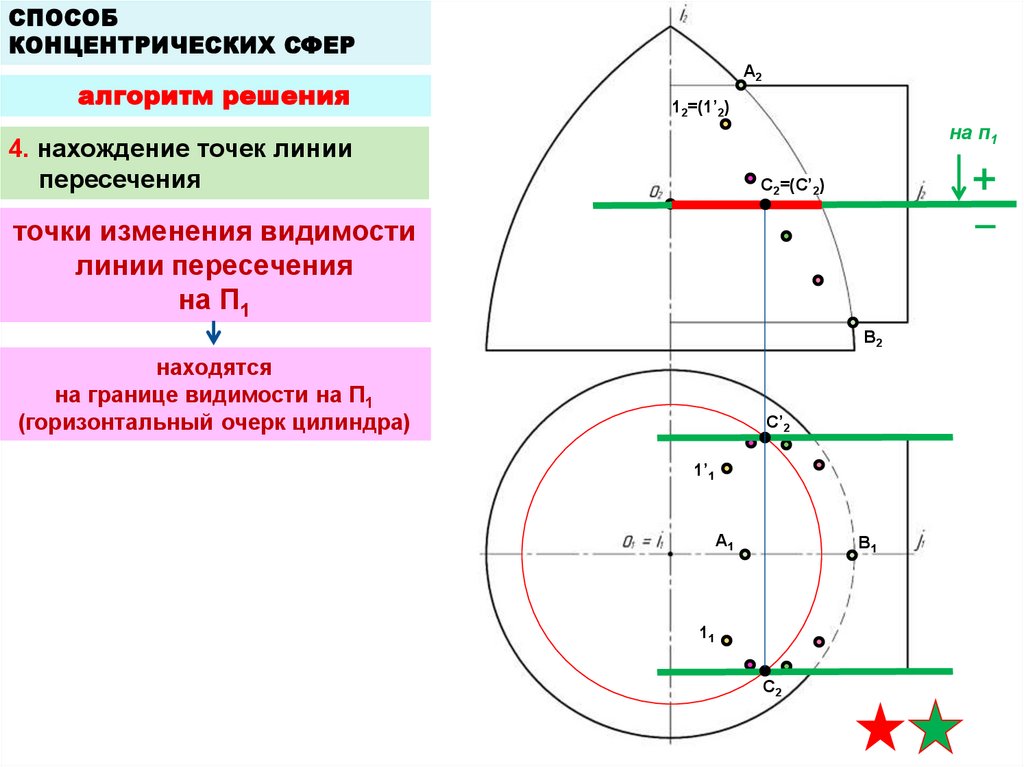
4. нахождение точек линии
пересечения
C2=(C’2)
точки изменения видимости
линии пересечения
на П1
B2
находятся
на границе видимости на П1
(горизонтальный очерк цилиндра)
C’2
1’1
A1
B1
11
C2
21.
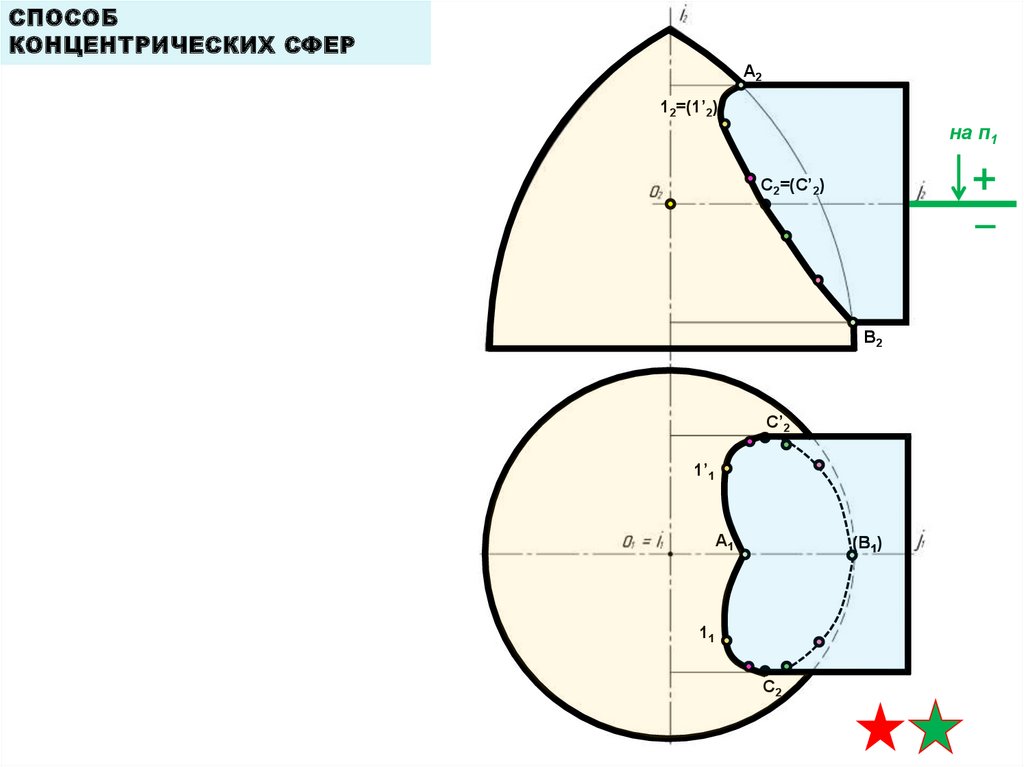
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
A2
12=(1’2)
на п1
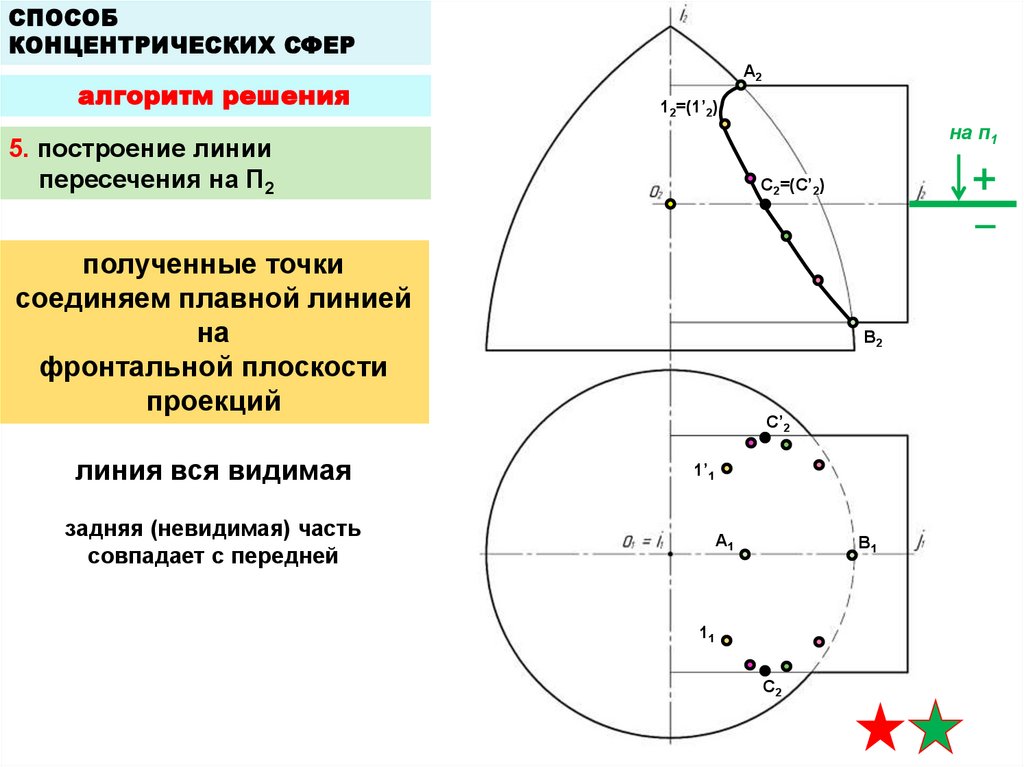
5. построение линии
пересечения на П2
C2=(C’2)
полученные точки
соединяем плавной линией
на
фронтальной плоскости
проекций
линия вся видимая
B2
C’2
1’1
задняя (невидимая) часть
совпадает с передней
A1
B1
11
C2
22.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
A2
12=(1’2)
на п1
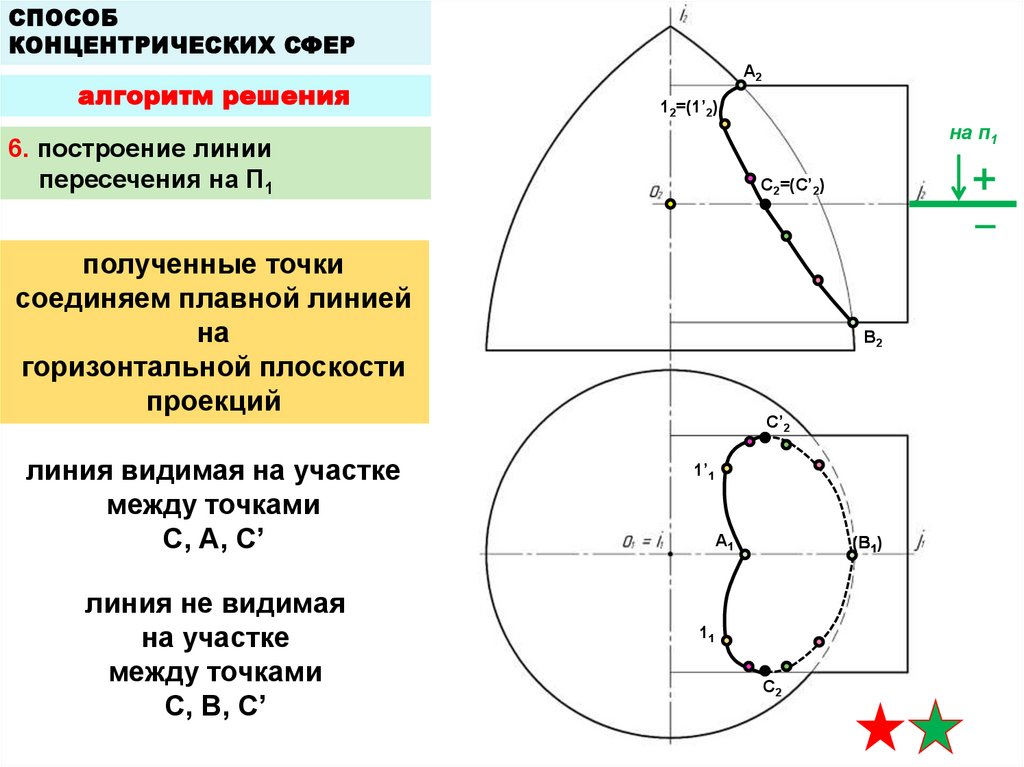
6. построение линии
пересечения на П1
C2=(C’2)
полученные точки
соединяем плавной линией
на
горизонтальной плоскости
проекций
линия видимая на участке
между точками
С, А, С’
линия не видимая
на участке
между точками
С, B, С’
B2
C’2
1’1
A1
(B
B1)
11
C2
23.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
A2
12=(1’2)
на п1
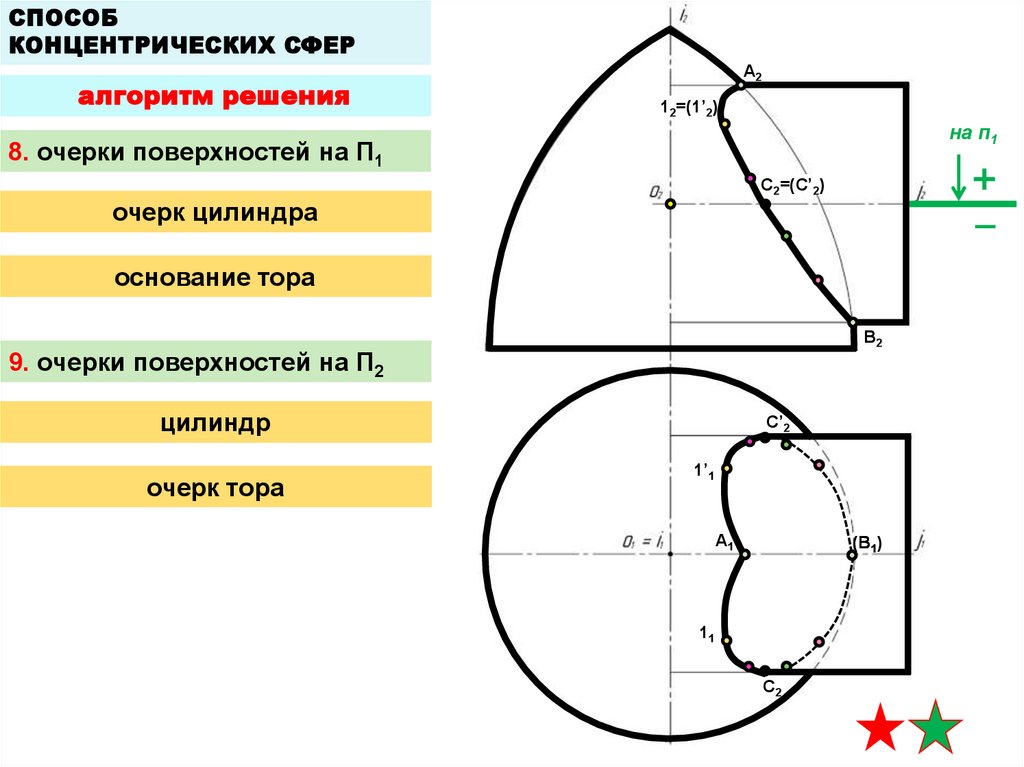
8. очерки поверхностей на П1
C2=(C’2)
очерк цилиндра
основание тора
B2
9. очерки поверхностей на П2
цилиндр
очерк тора
C’2
1’1
A1
(B
B1)
11
C2
24.
СПОСОБКОНЦЕНТРИЧЕСКИХ СФЕР
A2
12=(1’2)
на п1
C2=(C’2)
B2
C’2
1’1
A1
(B
B1)
11
C2
25.
Содержание лекцииметоды построения линии пересечения
двух поверхностей (Часть 2)
метод сфер-посредников
(способ вспомогательных секущих сфер)
основные термины (соосные, концентрические)
способ концентрических сфер
частный случай пересечения поверхностей
(теорема Монжа)
способ эксцентрических сфер
примеры решений задач из методички [2]
литература
26.
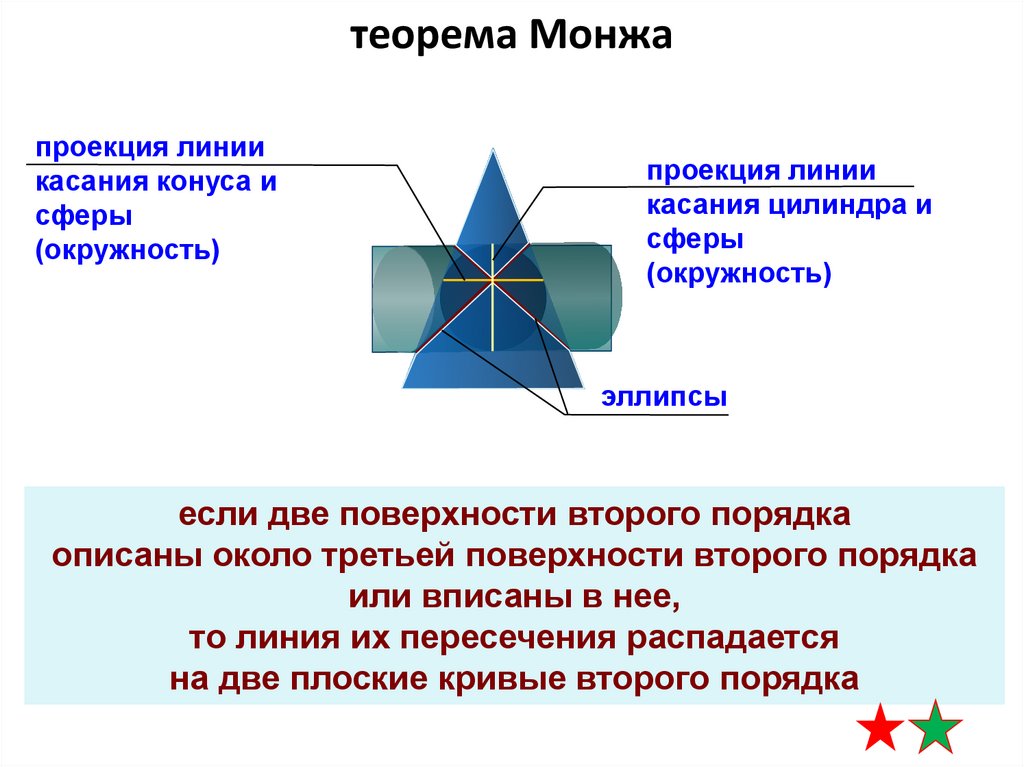
теорема Монжапроекция линии
касания конуса и
сферы
(окружность)
проекция линии
касания цилиндра и
сферы
(окружность)
эллипсы
если две поверхности второго порядка
описаны около третьей поверхности второго порядка
или вписаны в нее,
то линия их пересечения распадается
на две плоские кривые второго порядка
27.
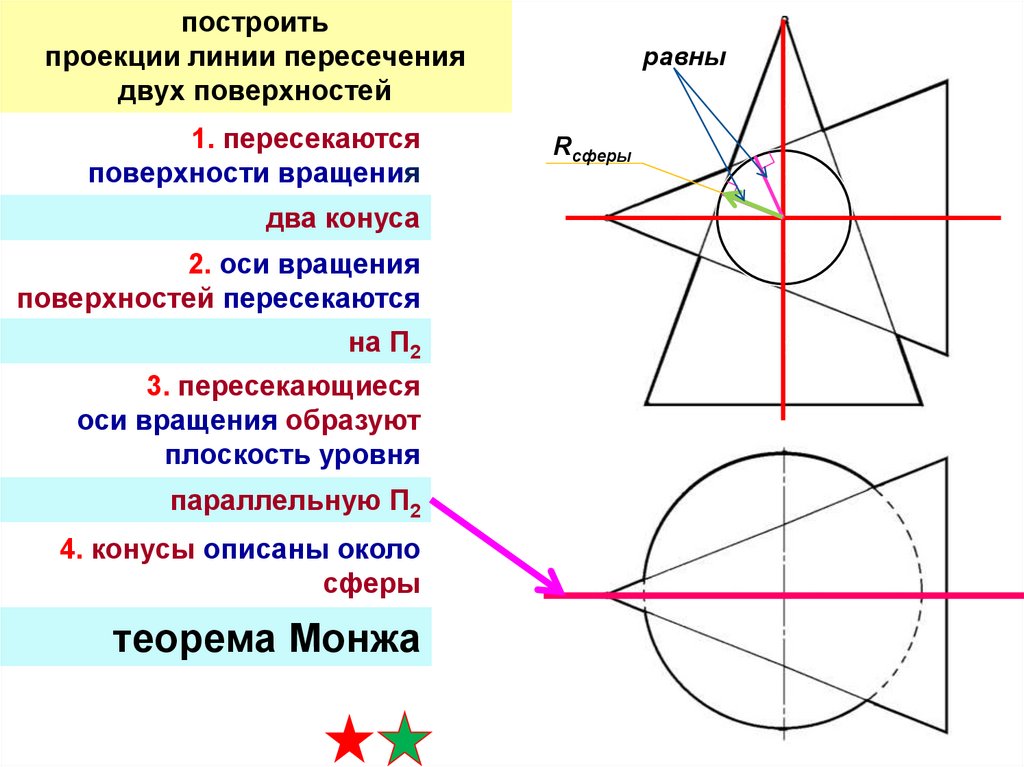
построитьпроекции линии пересечения
двух поверхностей
1. пересекаются
поверхности вращения
два конуса
2. оси вращения
поверхностей пересекаются
на П2
3. пересекающиеся
оси вращения образуют
плоскость уровня
параллельную П2
4. конусы описаны около
сферы
теорема Монжа
равны
Rсферы
28.
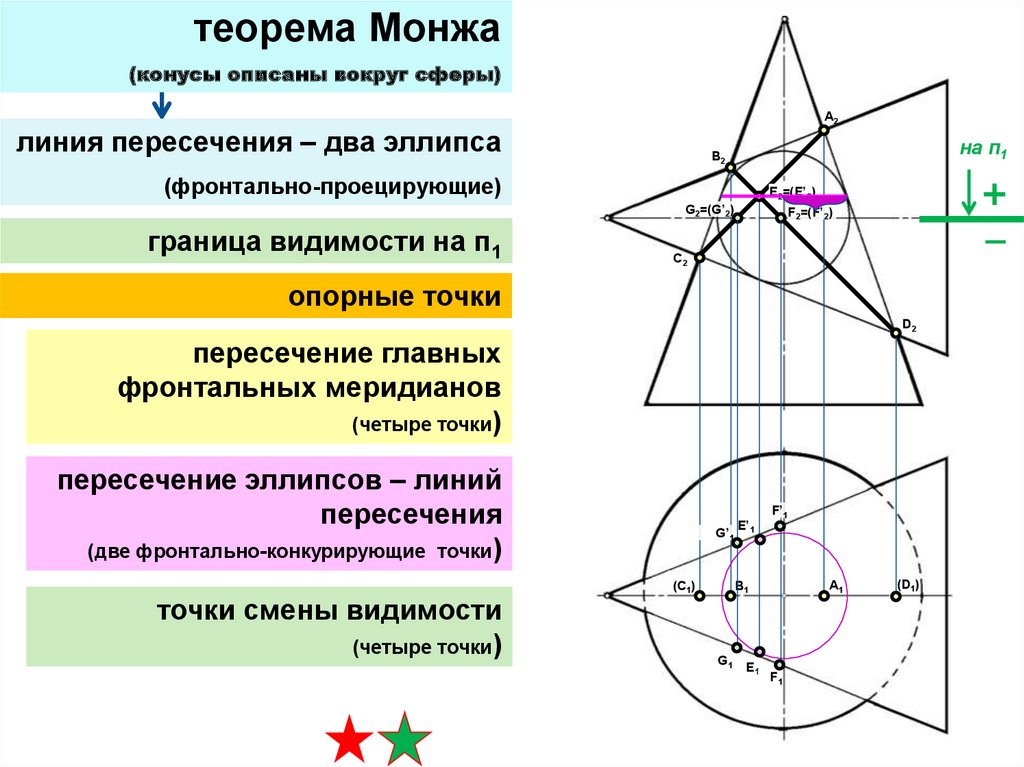
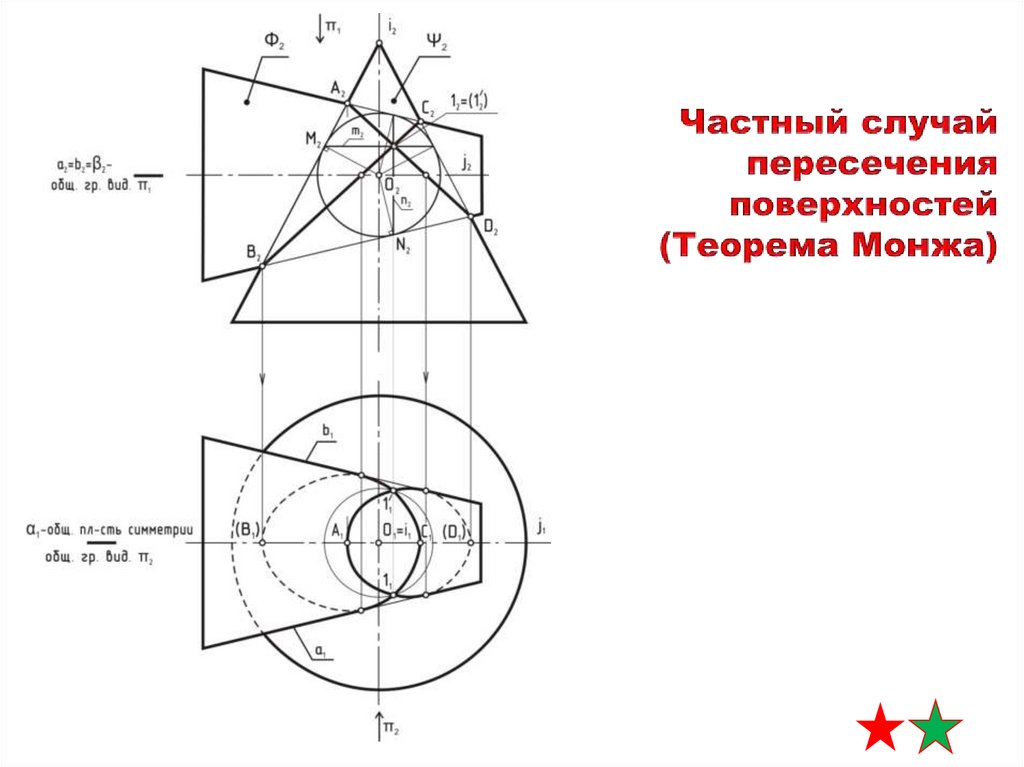
теорема Монжа(конусы описаны вокруг сферы)
A2
линия пересечения – два эллипса
на п1
B2
(фронтально-проецирующие)
E2=(E’2)
G2=(G’2)
граница видимости на п1
F2=(F’2)
C2
опорные точки
D2
пересечение главных
фронтальных меридианов
(четыре точки)
пересечение эллипсов – линий
пересечения
(две фронтально-конкурирующие точки)
точки смены видимости
(четыре точки)
G’1
(C1)
E’1
F’1
A1
B1
G1
E1
F1
(D1)
29.
теорема Монжа(конусы описаны вокруг сферы)
A2
линия пересечения – два эллипса
B2
(фронтально-проецирующие)
граница видимости на п1
на п1
22=(2’2)
E2=(E’2)
G2=(G’2)
12=(1’2)
F2=(F’2)
32=(3’2)
C2
42=(4’2)
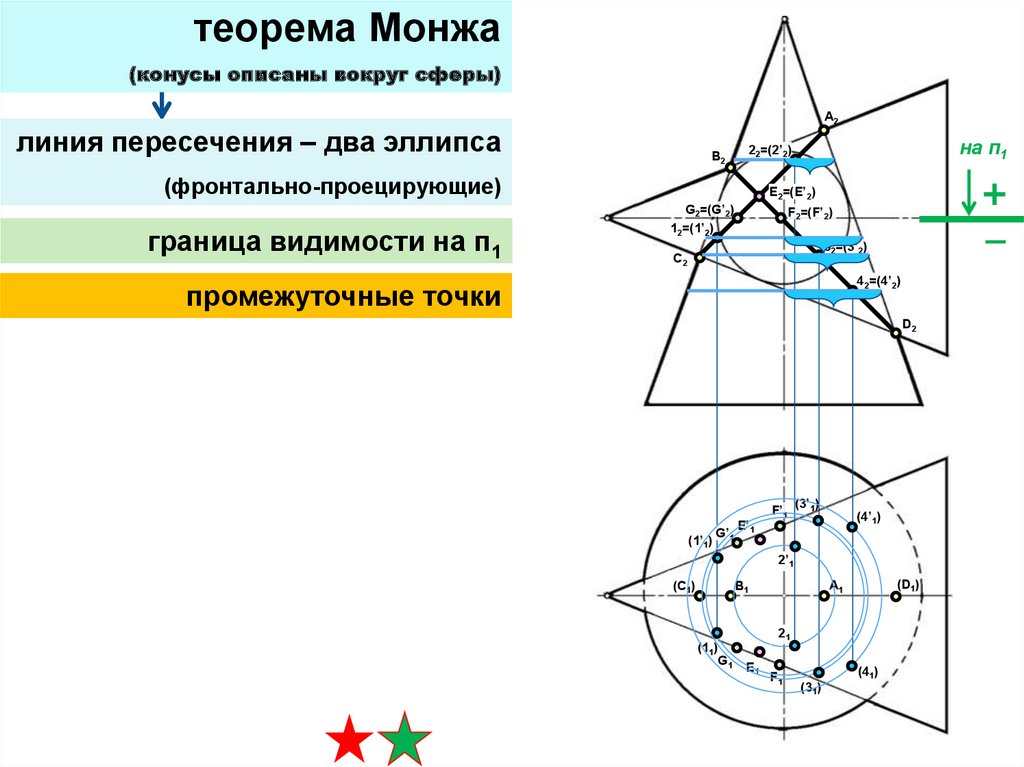
промежуточные точки
D2
(1’1)
G’1
E’1
F’1
(3’1)
(4’1)
2’1
(C1)
(D1)
A1
B1
21
(11)
G1
E1
F1
(41)
(31)
30.
теорема Монжа(конусы описаны вокруг сферы)
A2
линия пересечения – два эллипса
B2
(фронтально-проецирующие)
граница видимости на п1
на п1
22=(2’2)
E2=(E’2)
G2=(G’2)
12=(1’2)
F2=(F’2)
32=(3’2)
C2
42=(4’2)
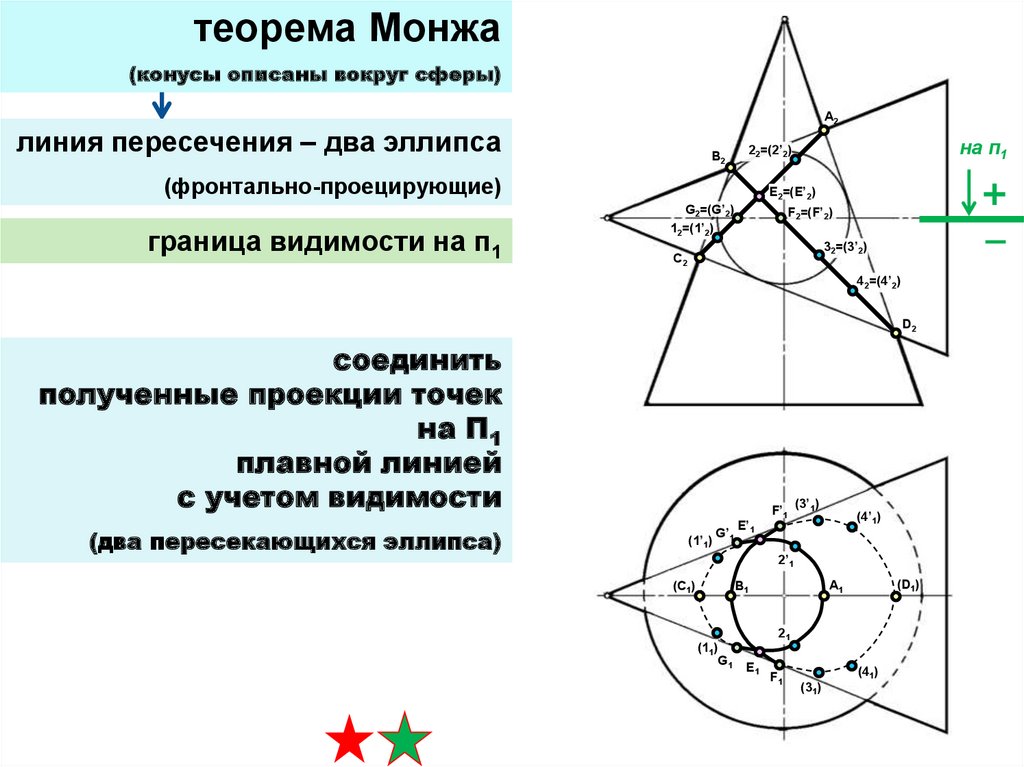
D2
соединить
полученные проекции точек
на П1
плавной линией
с учетом видимости
(два пересекающихся эллипса)
(1’1)
G’1
E’1
F’1
(3’1)
(4’1)
2’1
(C1)
(D1)
A1
B1
21
(11)
G1
E1
F1
(41)
(31)
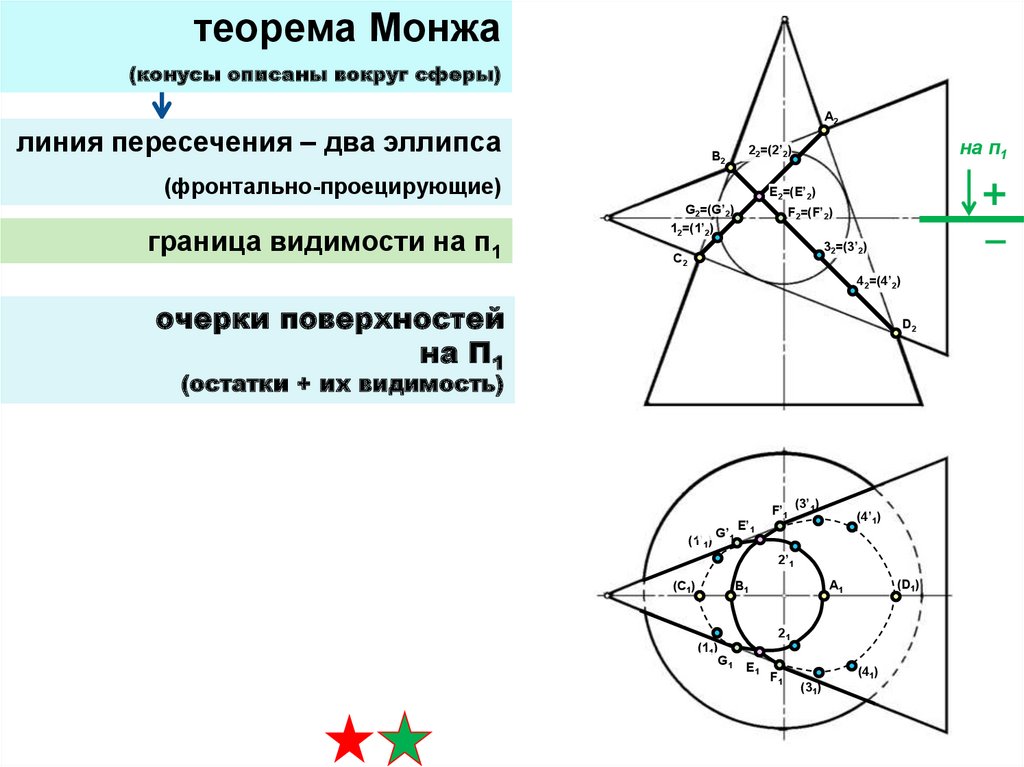
31.
теорема Монжа(конусы описаны вокруг сферы)
A2
линия пересечения – два эллипса
B2
(фронтально-проецирующие)
граница видимости на п1
на п1
22=(2’2)
E2=(E’2)
G2=(G’2)
12=(1’2)
F2=(F’2)
32=(3’2)
C2
42=(4’2)
очерки поверхностей
на П1
D2
(остатки + их видимость)
(1’1)
G’1
E’1
F’1
(3’1)
(4’1)
2’1
(C1)
(D1)
A1
B1
21
(11)
G1
E1
F1
(41)
(31)
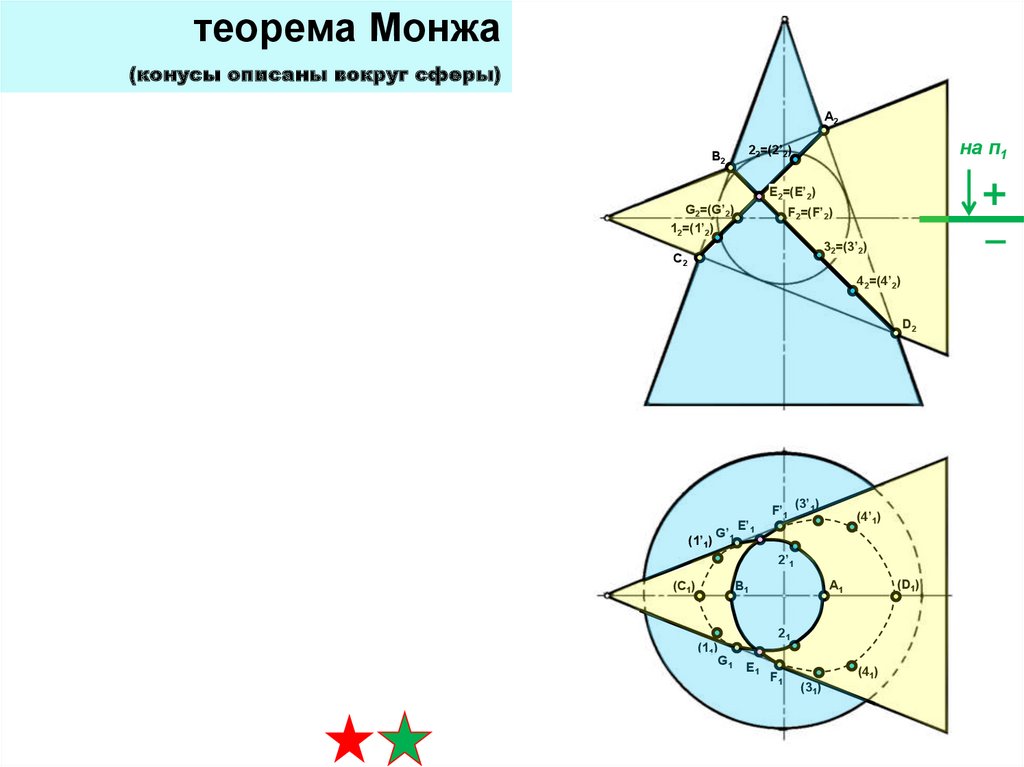
32.
теорема Монжа(конусы описаны вокруг сферы)
A2
B2
на п1
22=(2’2)
E2=(E’2)
G2=(G’2)
12=(1’2)
F2=(F’2)
32=(3’2)
C2
42=(4’2)
D2
(1’1)
G’1
E’1
F’1
(3’1)
(4’1)
2’1
(C1)
(D1)
A1
B1
21
(11)
G1
E1
F1
(41)
(31)
33.
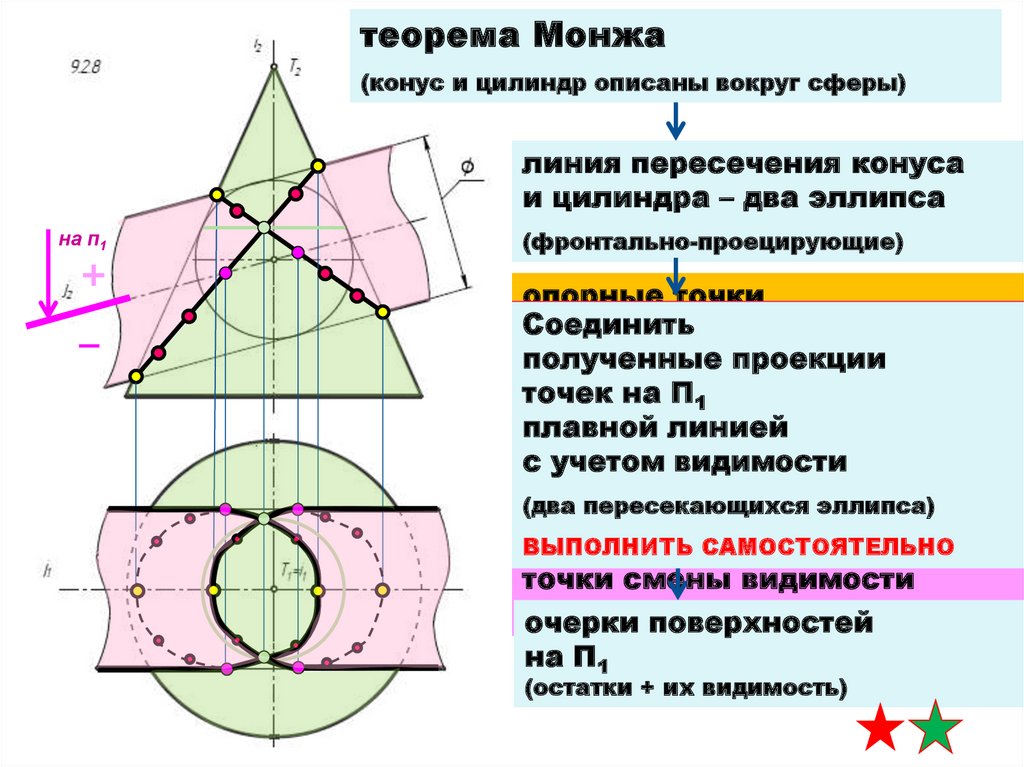
теорема Монжа(конус и цилиндр описаны вокруг сферы)
линия пересечения конуса
и цилиндра – два эллипса
на п1
(фронтально-проецирующие)
опорные точки
промежуточные точки
Соединить
пересечениепроекции
главных
полученные
фронтальных
меридианов
точек
на П1
построить
(четыре
точки
)на П1
плавной
линией
по
принадлежности
с учетом
видимости
к
конусу
Пересечение
эллипсов
(два пересекающихся эллипса)
(САМОСТОЯТЕЛЬНО)
(две фронтально-конкурирующие точки)
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
точки смены видимости
(четыре
точки
)
очерки
поверхностей
на П1
(остатки + их видимость)
34.
Содержание лекцииметоды построения линии пересечения
двух поверхностей (Часть 2)
метод сфер-посредников
(способ вспомогательных секущих сфер)
основные термины (соосные, концентрические)
способ концентрических сфер
частный случай пересечения поверхностей
(теорема Монжа)
способ эксцентрических сфер
примеры решений задач из методички [2]
литература
35.
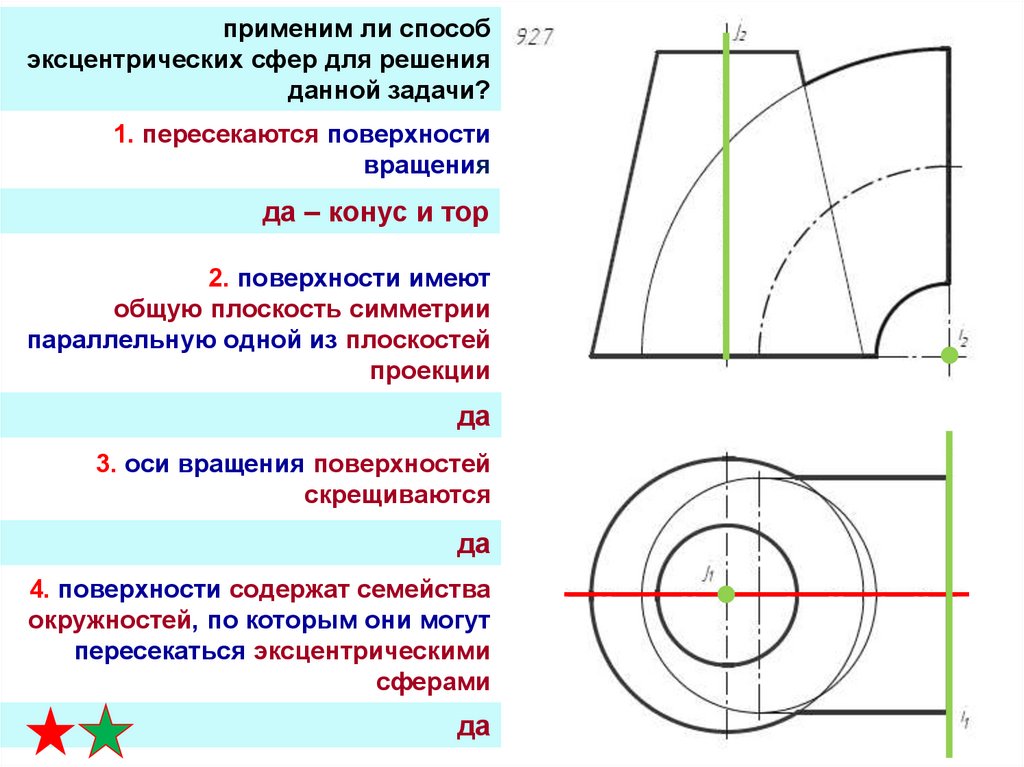
применим ли способэксцентрических сфер для решения
данной задачи?
1. пересекаются поверхности
вращения
да – конус и тор
2. поверхности имеют
общую плоскость симметрии
параллельную одной из плоскостей
проекции
да
3. оси вращения поверхностей
скрещиваются
да
4. поверхности содержат семейства
окружностей, по которым они могут
пересекаться эксцентрическими
сферами
да
36.
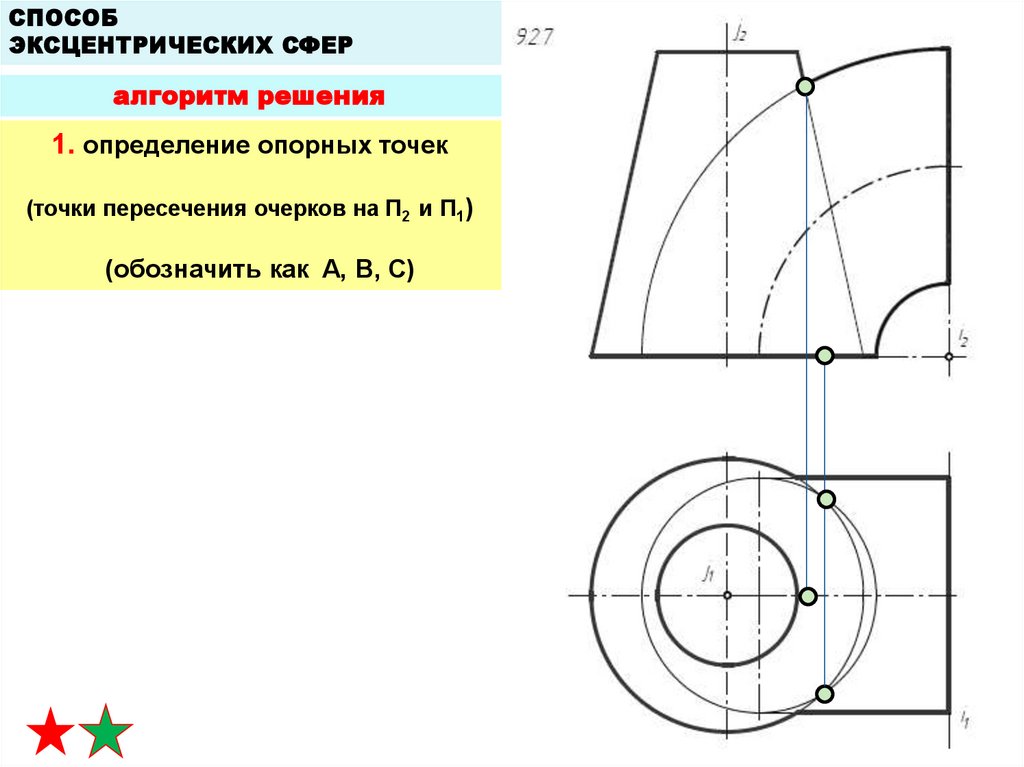
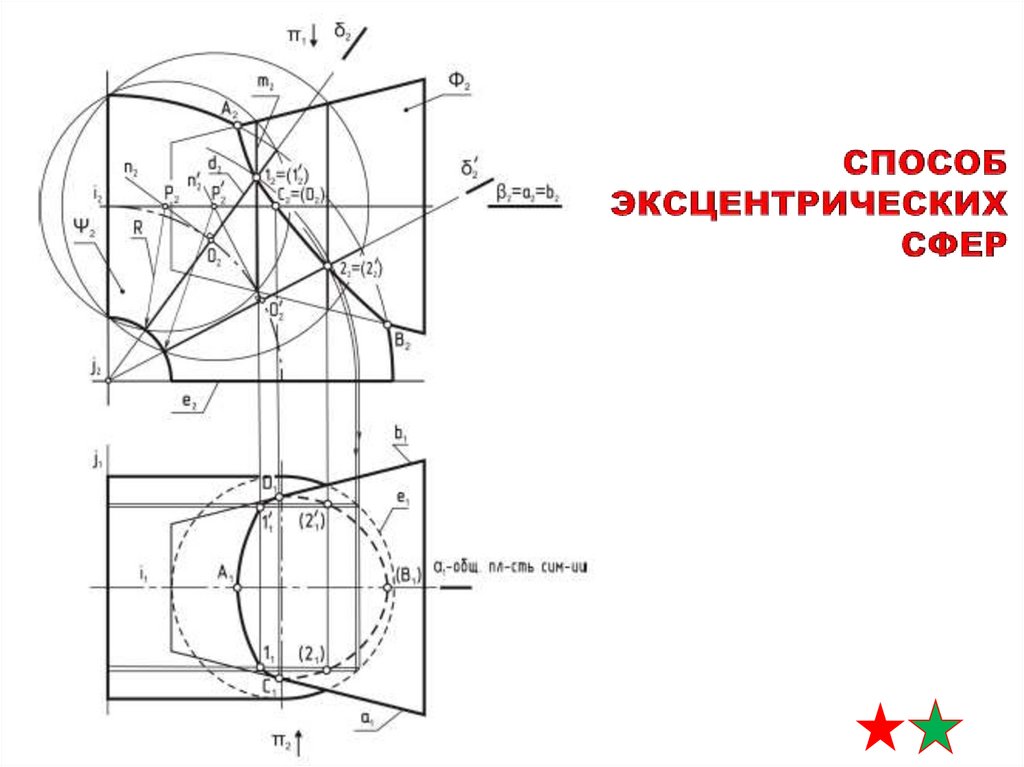
СПОСОБЭКСЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
1. определение опорных точек
(точки пересечения очерков на П2 и П1)
(обозначить как A, B, C)
37.
СПОСОБЭКСЦЕНТРИЧЕСКИХ СФЕР
σ2
алгоритм решения
окружность
центр
окружности
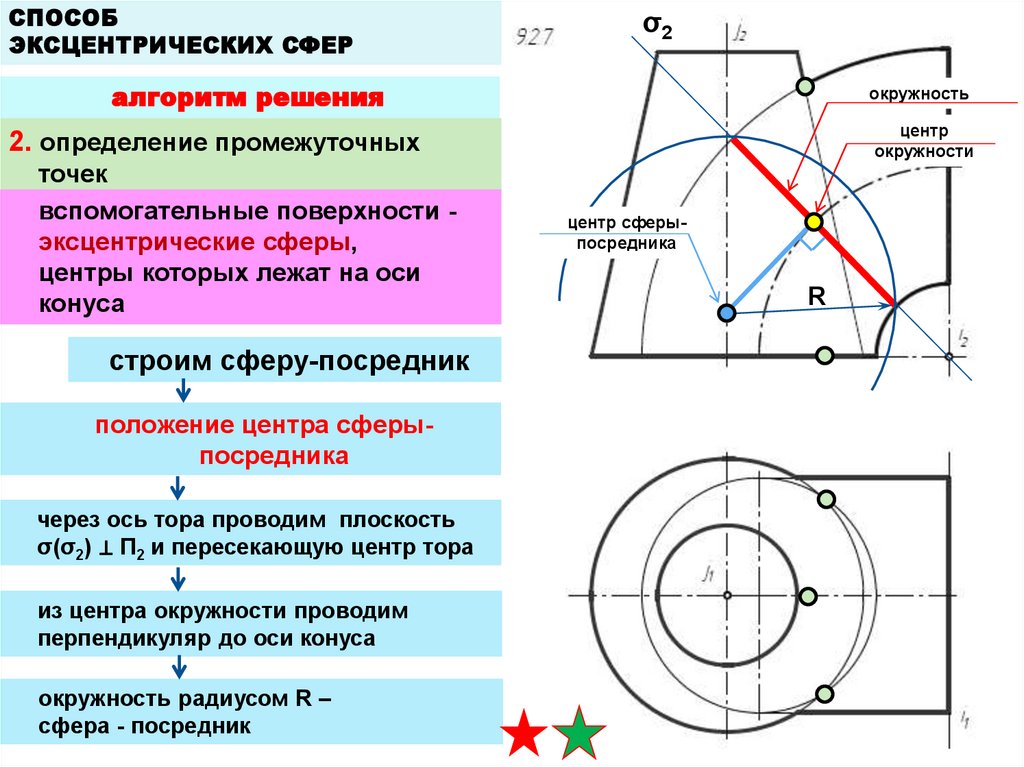
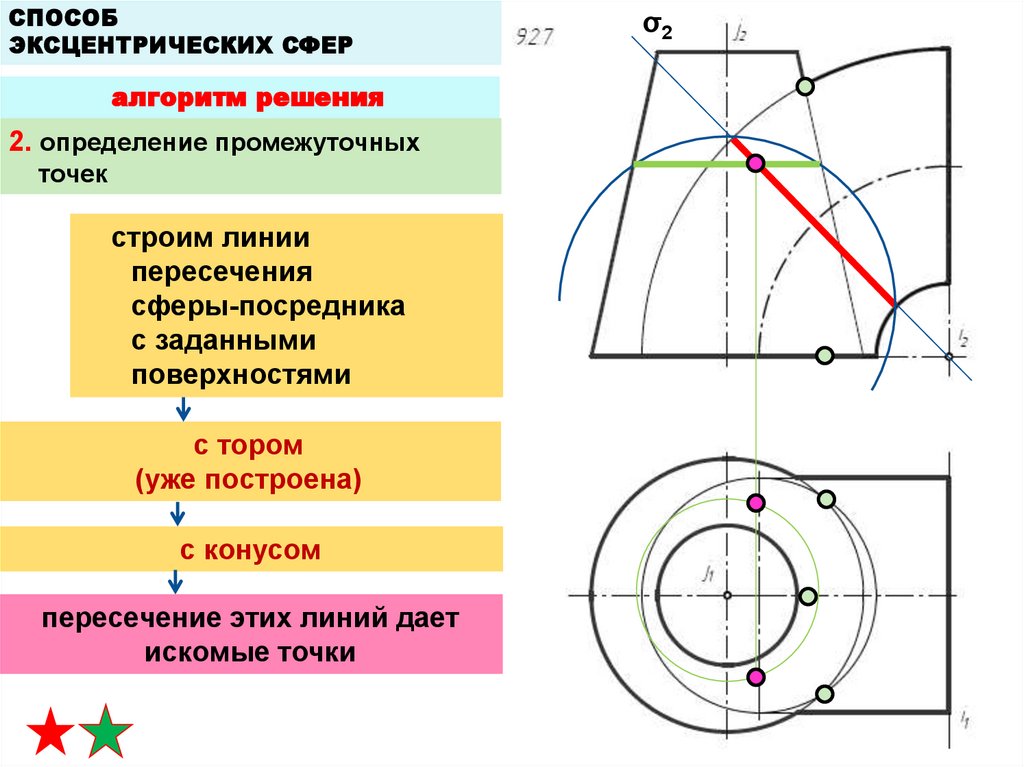
2. определение промежуточных
точек
вспомогательные поверхности эксцентрические сферы,
центры которых лежат на оси
конуса
строим сферу-посредник
положение центра сферыпосредника
через ось тора проводим плоскость
σ(σ2) ⊥ П2 и пересекающую центр тора
из центра окружности проводим
перпендикуляр до оси конуса
окружность радиусом R –
сфера - посредник
центр сферыпосредника
R
38.
СПОСОБЭКСЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
2. определение промежуточных
точек
строим линии
пересечения
сферы-посредника
с заданными
поверхностями
с тором
(уже построена)
с конусом
пересечение этих линий дает
искомые точки
σ2
39.
СПОСОБЭКСЦЕНТРИЧЕСКИХ СФЕР
алгоритм решения
3.4.
Построение
Определение
точек смены
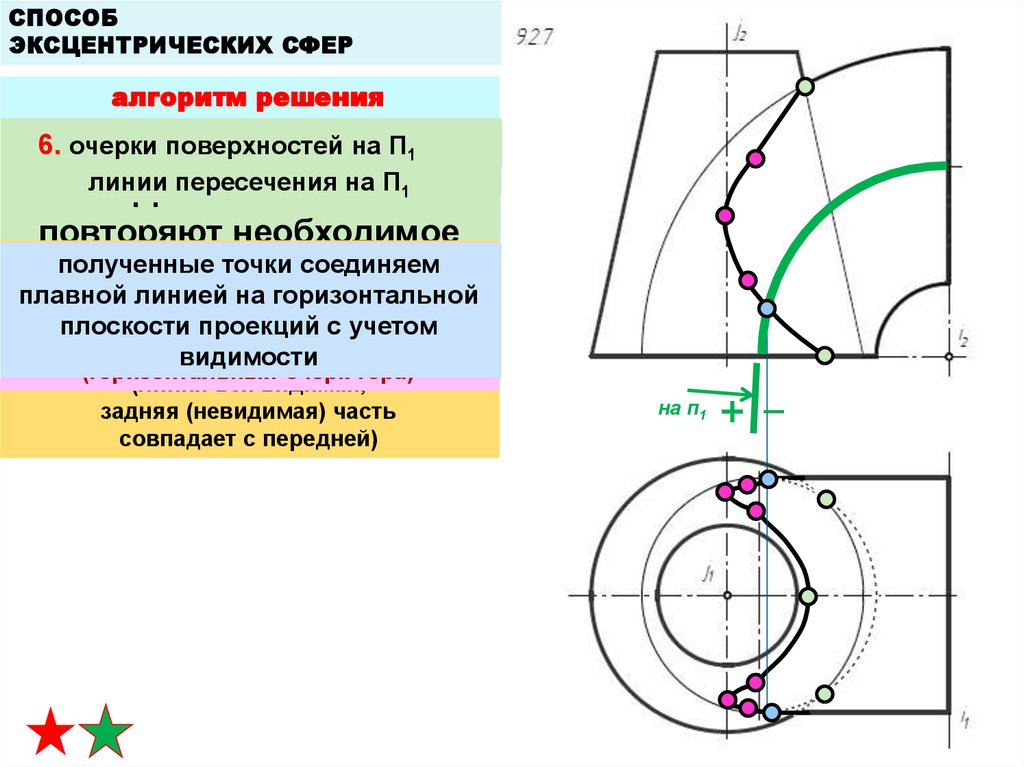
6.
очерки
поверхностей
на П1
5.
Построение
линии
пересечения
видимости
на П1 на Пна
линии
пересечения
Действия
п. 22 П1
повторяют необходимое
Точки смены
видимости
Полученные
точки
соединяем
полученные
количество
раз
для
линии
пересечения
на П1
плавной
плавной
линией
налинией
горизонтальной
находятся
получения
точекс линии
на фронтальной
плоскости
проекций
учетом
на
границе
видимости
плоскости
проекций
видимости
пересечения
(горизонтальный очерк тора)
(линия вся видимая,
задняя (невидимая) часть
совпадает с передней)
на п1
40.
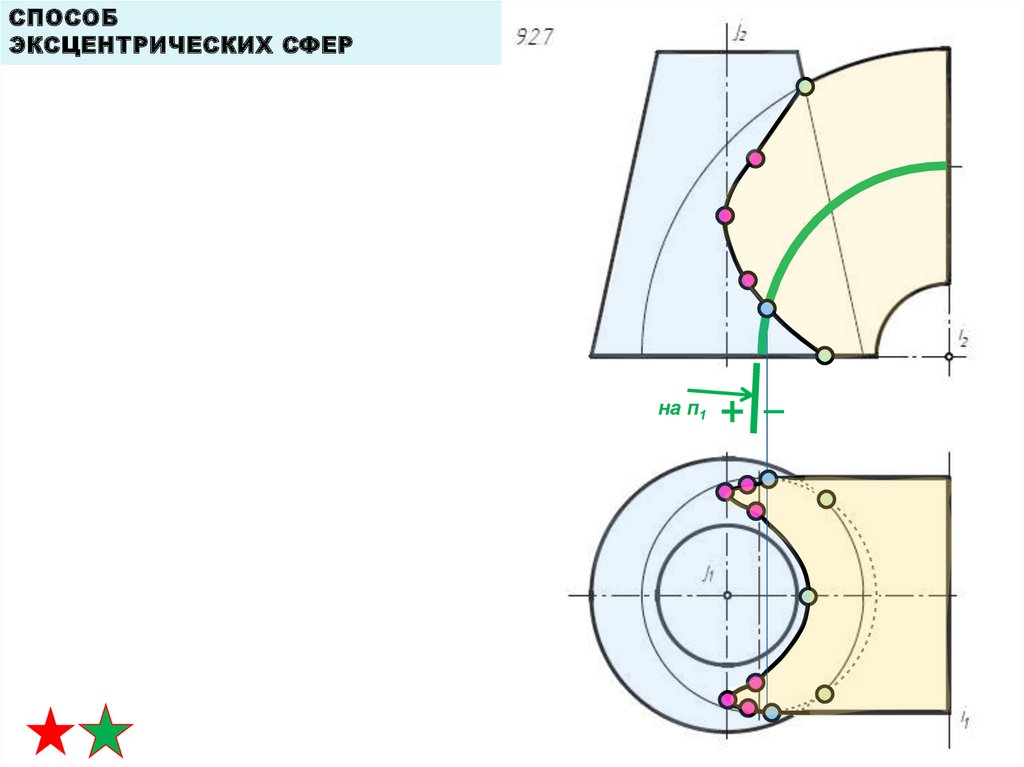
СПОСОБЭКСЦЕНТРИЧЕСКИХ СФЕР
на п1
41.
Содержание лекцииметоды построения линии пересечения
двух поверхностей (Часть 2)
метод сфер-посредников
(способ вспомогательных секущих сфер)
основные термины (соосные, концентрические)
способ концентрических сфер
частный случай пересечения поверхностей
(теорема Монжа)
способ эксцентрических сфер
примеры решений задач из методички [2]
литература
42.
43.
44.
45.
литература1) Адонкина Е. В. Начертательная геометрия и Инженерная графика.
Мультимедийное сопровождение лекций : электронный курс для
преподавателей и студентов архитектурно-строительных университетов [
Электронный ресурс ] / Е. В. Адонкина; Новосиб. гос. архитектур.-строит. ун-т
(Сибстрин). – Электрон. текст., граф. дан. – Новосибирск : НГАСУ (Сибстрин),
2011.
2) Блинова Л.В., Куркина Л.В. Пересечение поверхностей [Электронный ресурс]:
Учебно-методическое пособие.— Электрон. дан.— Барнаул: АлтГТУ, 2015.—
Режим доступа: http://new.elib.altstu.ru/eum/download/ngig/Blinova_peresech.pdf,
авторизованный







 drafting
drafting








