Теория и методика начального общего образования

1.

ТЕОРИЯ И МЕТОДИКА НАЧАЛЬНОГО
ОБЩЕГО ОБРАЗОВАНИЯ
Дополнительная профессиональная
программа профессиональной
переподготовки

2.

Организация математического
образования в начальном
общем образовании

3.

Ирина Евгеньевна ДЕВЯТОВА
доцент, кандидат педагогических наук,
доцент, старший научный сотрудник
кафедры ЧИППКРО
сертифицированный практический
психолог, ассоциированный член Федерации
психологов -консультантов,
эксперт Учебно-методического
объединения в сфере общего образования
в Челябинской области
специалист, осуществляющий анализ
профессиональной деятельности
педагогических работников на территории
Челябинской области
победитель конкурса Фонда грантов
Президента РФ в 2020 году

4.

Задачи в обучении
математике в начальных классах
Лекция 3

5.

План:
1) Определение «задача».
2) Простые задачи в начальном курсе
математики.
3) Составные задачи в начальном курсе
математики.

6.

Определение «задача».
1 вопрос

7.

Задача: определение
Арифметическая
задача
Математическая
задача
- требование в определении
числового значения
искомой величины по
известным числовым
значениям других величин
и зависимостям,
выраженным в словесной
форме, которые
связывают все
известные и неизвестные
величины между собой.
- связный лаконический
рассказ, в котором
введены значения
некоторых величин и
предлагается отыскать
другие неизвестные
значения величин,
зависимые от данных и
связанные с ними
определенными
отношениями, указанными
в условии.

8.

Решить математическую задачу
- это значит найти такую последовательность
общих положений математики, применяя
которые к условиям задачи получаем то, что
требуется найти ответ.
решение как результат, т.е.
как ответ на вопрос,
поставленный в задаче
решение как процесс
нахождения этого результата

9.

Конструкции задач
В начале текста дано условие, которое
выражено повествовательными
предложениями, а затем следует требование,
выраженное вопросительным предложением.
В гараже стояло 4 машины.
По вызову из гаража
выехало 3 машины. Сколько
машин осталось стоять в
гараже?
Часть условия представлена
повествовательным предложением в начале
текста, а затем идет вопросительное
предложение, содержащее вопрос и другую
часть условия.
В гараже стояло 4 машины.
Сколько машин осталось в
гараже, если из гаража
уехало 3 машины?
Часть условия представлена
повествовательным предложением в начале
текста. Затем дано второе повествовательное
предложение, содержащее требование и еще
часть условия.
В гараже стояло 4 машины.
Найдите количество
машин, оставшихся в
гараже, после того, как 3
машины уехало.
Текст задачи представляет собой одно
вопросительное предложение, в котором
сначала идет вопрос, а затем условие.
Сколько машин осталось в
гараже после того, как 3 из
4 машин уехали?

10.

Простые задачи в начальном
курсе математики
2 вопрос

11.

Планируемые предметные результаты

12.

Классификация простых задач
(по М.А. Бантовой)
Первая группа - простые задачи, при решении которых дети
усваивают конкретный смысл каждого из арифметических
действий.
1) Нахождение
суммы двух чисел
Во дворе гуляли 3 мальчика и 2 девочки. Сколько всего
детей гуляло во дворе?
2) Нахождение
остатка
На тарелке лежало 6 пирожков. Два пирожка дети съели.
Сколько пирожков осталось на тарелке?
3) Нахождение
произведения
В живом уголке хомячки жили в четырех клетках, по 2
хомячка в каждой клетке. Сколько всего хомячков в
живом уголке?
5) Деление на
равные части
Мама раздала 6 апельсинов поровну 3 детям. Сколько
апельсинов досталось каждому ребенку?
6) Деление по
содержанию
Учительница раздала 10 тетрадей ученикам по 2 тетради
каждому. Сколько учеников получило тетради?

13.

Классификация простых задач
(по М.А. Бантовой)
Вторая группа - простые задачи, при решении которых
учащиеся усваивают связь между компонентами и
результатами арифметических действий.
1) Нахождение первого слагаемого Во дворе гуляли несколько мальчиков и 2
по известному значению суммы и девочки. Всего во дворе гуляло 5 детей.
второму слагаемому
Сколько мальчиков гуляло во дворе?
2) Нахождение второго слагаемого
по известному значению суммы и
первому слагаемому.
Во дворе гуляли 3 мальчика и несколько
девочек. Всего во дворе гуляло 5 детей.
Сколько девочек гуляло во дворе?)
3) Нахождение уменьшаемого по
известным вычитаемому и
значению разности.
На тарелке было несколько пирожков. Когда
два пирожка съели, на тарелке осталось 4
пирожка. Сколько пирожков было на
тарелке?)
4) Нахождение вычитаемого по
известным уменьшаемому и
значению разности.
На тарелке было 6 пирожков. Когда несколько
пирожков съели, на тарелке осталось 4
пирожка. Сколько пирожков съели?

14.

Классификация простых задач
(по М.А. Бантовой)
Вторая группа - простые задачи, при решении которых
учащиеся усваивают связь между компонентами и
результатами арифметических действий.
5) Нахождение первого множителя по
известным значению произведения и
второму множителю.
Неизвестное число умножили на 4 и
получили 20. Найти неизвестное число.
6) Нахождение второго множителя по
известным значению произведения и
первому множителю.
7 умножили на неизвестное число и
получили 35. Найти неизвестное число.
7) Нахождение делимого по известным
делителю и значению частного.
Неизвестное число разделили на 4 и
получили 7. Найти неизвестное число.
8) Нахождение делителя по известным
делимому и значению частного.
32 разделили на неизвестное число и
получили 8. Найти неизвестное число.

15.

Классификация простых задач
(по М.А. Бантовой)
Третья группа – простые задачи, при решении которых
раскрываются понятия разности и кратного отношения. К
ним относятся простые задачи, связанные с понятием
разности, и простые задачи, связанные с понятием кратного
отношения.

16.

Простые задачи, связанные с понятием разности
1) Разностное сравнение чисел (1
вид).
У Кати 3 шарика, а у Маши 5 шариков. На
сколько шариков у Маши больше, чем у
Кати?
2) Разностное сравнение чисел (2
вид).
У Кати 3 шарика, а у Маши 5 шариков. На
сколько шариков у Кати меньше, чем у
Маши?
3) Увеличение числа на несколько
единиц (прямая форма).
У Кати 3 шарика, а у Маши на 2 шарика
больше, чем у Кати. Сколько шариков у
Маши?
4) Увеличение числа на несколько
единиц (косвенная форма).
У Кати 3 шарика, это на 2 шарика меньше,
чем у Маши. Сколько шариков у Маши?
5) Уменьшение числа на несколько
единиц (прямая форма).
У Маши 5 шариков, а у Кати на 2 шарика
меньше, чем у Маши. Сколько шариков у
Кати?
6) Уменьшение числа на несколько
единиц (косвенная форма).
У Маши 5 шариков, это на 2 шарика больше,
чем у Кати. Сколько шариков у Кати?

17.

Простые задачи, связанные с понятием кратного отношения
7) Кратное сравнение чисел или
нахождение кратного отношения
двух чисел (1 вид).
У Кати 10 шариков, а у Маши 5 шариков. Во
сколько раз у Маши шариков больше, чем у
Кати?
8) Кратное сравнение чисел или
нахождение кратного отношения
двух чисел (2 вид).
У Кати 10 шариков, а у Маши 5 шариков. Во
сколько раз у Кати шариков меньше, чем у
Маши?
9) Увеличение числа в несколько
раз (прямая форма).
У Кати 3 шарика, а у Маши в 2 раза больше,
чем у Кати. Сколько шариков у Маши?
10) Увеличение числа в несколько
раз (косвенная форма).
У Кати 5 шариков, это в 2 раза меньше, чем
у Маши. Сколько шариков у Маши?
11) Уменьшение числа в несколько
раз (прямая форма).
У Маши 10 шариков, а у Кати в 2 раза
меньше, чем у Маши. Сколько шариков у
Кати?
12) Уменьшение числа в несколько
раз (косвенная форма).
У Маши 10 шариков, это в 2 раза больше,
чем у Кати. Сколько шариков у Кати?

18.

Этапы обучения решению простых задач
1 - подготовительный этап;
2 - этап ознакомления с задачей и
формирование умений работать над задачей;
3 - этап отработки этих умений в процессе
решения различных задач.

19.

Подготовительный этап: базовые умения
учащихся
• слушать и понимать тексты задач различной
структуры;
• правильно представлять и моделировать
ситуации, предлагаемые учителем;
• правильно выбирать действие в соответствии с
ситуацией;
• обосновывать выбор действия, с помощью
которого решается задача;
• составлять математическое выражение с
выбранным действием;
• осуществлять проверку правильности решения
задачи.

20.

Второй этап обучения
решению задач: понятие
задачи
• ознакомление с
понятием «задача» и
её существенными
признаками;
• обучение анализу
задачи, формам
записи ее решения и
ответа, способам
проверки
правильности
решения задачи.

21.

Усвоение структуры задачи: виды
упражнений (по Н.Б.Истоминой)
1)
2)
3)
4)
5)
6)
7)
Сравнение текстов задач.
Постановка вопроса учащимися к условию.
Составление условия к данному вопросу.
Задачи с недостающими данными.
Задачи с лишними данными.
Преобразование вопроса, условия, данных задачи.
Составление задач по рисунку, краткой записи, по
решению.
Для сравнения целесообразно подбирать такие пары задач, которые
имеют: а) одинаковые условия, но различные вопросы; б) одинаковые
вопросы, но различия в условиях; в) одинаковые решения, хотя смысл
одного и того же действия в каждой задаче различен.

22.

Третий этап обучения решению задач:
формирование у младших школьников
обобщенного умения решения задач
– знание о задачах, методах и способах
решения, приемах, помогающих решению в
процессе работы над задачей, этапах этого
процесса, назначении и содержании каждого
этапа;
– умение расчленять текст задачи на составные
части, использовать различные методы
решения, адекватно применять приемы,
помогающие понять содержание задачи,
составить план решения, выполнить его,
проверить решение.

23.

Цель работы над простой задачей: обучение
ребенка самостоятельной работе над
текстовой формой простой задачи
Формируемые умения:
• моделирование заданной в тексте задачи
ситуации;
• выбор арифметического действия и
составление математического выражения;
• вычисление значения составленного
выражения;
• запись ответа задачи;
• проверка правильности решения задачи.

24.

Содержание и методика
формирования
компонентов общего приема
решения задач

25.

Прямой анализ задачи
предполагает, что из текста задачи
выделяется ряд простых задач, входящих в
ее состав, последовательное решение
которых приводит к решению задачи.
В процессе прямого анализа движение
мысли идет от данных к вопросу.

26.

Из пластилина и спичек
Саша сделал 5 разных
поделок, а Дима – на 2
поделки меньше .
Сколько всего поделок
сделали мальчики?

27.

1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
Прочитайте вопрос задачи. Можно ли сразу ответить на
вопрос задачи?
Какая задача по составу?
Выделите первую простую задачу.
Каким действием решается эта задача? (вычитанием);
Почему?
Запишите решение первой простой задачи.
(5 -2 = 3 (поделки)).
Ответили мы на вопрос исходной задачи? (Нет.)
Выделите вторую простую задачу.
Каким действием будем решать эту задачу?
(сложением). Почему?
Запишите решение второй простой задачи.
(5 + 3 = 8 (поделок)).
Скажите ответ второй простой задачи.
Ответили мы на вопрос исходной задачи? (Да.)
Скажите план решения исходной задачи.

28.

Обратный анализ задачи
При обратном анализе движение мысли
осуществляется от вопроса к данным и с каждым
разом необходимо уточнять, какие величины
нужно знать, чтобы найти значение неизвестной
величины.
Обратный анализ полезно сопровождать схемой.

29.

Из пластилина и спичек
Саша сделал 5 разных
поделок, а Дима – на 2
поделки меньше .
Сколько всего поделок
сделали мальчики?

30.

1) Прочитайте вопрос задачи. (Сколько всего поделок
сделали мальчики?)
2) Можно ли сразу ответить на вопрос задачи? (Нет)
3) Каких два значения надо знать, чтобы ответить на
вопрос задачи? (Сколько поделок сделал Саша и
Дима.)
4) Какое значение нам уже известно? (Сколько поделок
сделал Саша.)
5) Что неизвестно? (Сколько поделок сделал Дима.)
6) Какие значения надо знать, чтобы вычислить, сколько
поделок сделал Дима? (Сколько поделок сделал Саша
и на сколько поделок меньше сделал Дима.)
7) Какие из этих значений мы знаем? (Мы знаем оба этих
значения.)
8) Скажите план решения задачи. (Сначала мы узнаем,
сколько поделок сделал Дима, а затем, сколько всего
поделок сделали мальчики.)

31.

Пример анализа задачи
ЗАДАЧИ
?
5
АНАЛИЗ
?
5
2

32.

Пример анализа задачи
8
5
1)
+
3
5
_
2
План решения задачи
2)

33.

Смешанный анализ задачи
При смешанном анализе используется частично
первый и второй вид анализ. Строгой
последовательности в этом виде анализа нет.
• Можем ли мы сразу ответить на вопрос задачи?
(Нет)
• Почему? (Не знаем, сколько поделок сделал Дима.)
• А можем ли узнать, сколько поделок сделал Дима?
(Да.)
• Почему? (Знаем, сколько поделок сделал Саша и на
сколько поделок меньше сделал Дима.)
• Скажите план решения задачи.

34.

Решение задачи
1) Задача может быть решена устно с
проговариванием тех действий, которые
приведут к ответу.
2) Решение задачи записывается.
При этом используют запись решения задачи по
действиям. Причем, различают запись по
действиям без пояснения, с кратким пояснением, с
подробным пояснением. Полезно использовать
разные формы записи решения задачи.

35.

Задача: Из пунктов А и В навстречу друг
другу вышли 2 автомобиля. Скорость
первого автомобиля 60 км/ч, скорость
второго автомобиля в 2 раза больше, чем у
первого. Через 2 часа эти автомобили
встретились. Каково расстояние между
пунктами А и В?

36.

Способы записи решения задачи
а) Запись решения задачи в виде плана запись только вопросов без выполнения
действий.
1. Найдем скорость второго автомобиля.
2. Найдем путь, пройденный вторым
автомобилем.
3. Находим путь, пройденный первым
автомобилем.
4. Найдем расстояние между пунктами А и В.

37.

Способы записи решения задачи
б) Запись решения задачи по действиям с
пояснением или без пояснения.
1) 60 Х 2 = 120 (км/ч)
2) 120 : 2 = 240 (км)
3) 60 Х 2 = 120 (км)
4) 240 + 120 = 360 (км)

38.

Способы записи решения задачи
в) Запись решения с помощью выражения,
вычислив значение которого, можно
ответить на вопрос задачи.
(60 Х 2) : 2 + 60 Х 2 = 360 (км)

39.

Способы записи решения задачи
г) Запись решения задачи по действиям с вопросами.
1) Какова скорость движения второго автомобиля?
60 Х 2 = 120 (км/ч)
2) Каков путь, пройден вторым автомобилем до
встречи?
120 : 2 = 240 (км/ч)
3) Каков путь, пройден первым автомобилем до
встречи?
60 Х 2 = 120 (км/ч)
4) Каково расстояние между пунктами А и В?
120 + 240 = 360 (км)

40.

Способы записи решения задачи
е) Запись решения задачи выполняется в
таблице.

41.

Способы записи решения задачи
ж) Решение задачи можно записать с
помощью программы для компьютера.
з) Решение задач геометрического
содержания, полезно выполнять путем
построения требуемой фигуры с помощью
чертежных инструментов.

42.

Алгебраический способ решения
задачи
Задача: Купили 3 кг помидоров и 4 кг огурцов.
Сколько килограммов овощей купили?
Если через х обозначить «сколько всего
килограммов овощей купили», то по данной
задаче можно составить три уравнения:
3+4=х
х–3=4
х–4=3

43.

Геометрический способ решения
задачи
Задача: На тарелке 2 пирожка с повидлом,
после того как добавили еще несколько
пирожков с капустой, стало 7 пирожков.
Сколько пирожков добавили на тарелку?

44.

Примеры оформления ответа задачи
В учебнике:
На доске:
В тетради ученика:
В 1 классе ответ подчеркивается.
Полный ответ проговаривается.
Варианты записи ответов:
Ответ: 420 км.
Полный ответ проговаривается в слух.
Ответ: расстояние между городами между городами А и В равно 420 км.
Ответ не следует начинать с числа, а наименование возле числа можно писать
сокращенно.

45.

Задания после решения задачи
1. Изменить условия задачи так, чтобы она решалась
меньшим числом действий.
2. Постановка нового вопроса к уже решенной задаче.
3. Постановка всех вопросов, ответы на которые можно
найти по данному тексту задачи.
4. Сравнение содержания данной задачи с
содержанием и решением другой задачи, у которых
есть как общие, так и различные элементы. (Условие,
вопрос, числа, одинаковое число действий, сюжет
задачи и т. д.)
5. Решение задачи другим способом или другим
методом.
6. Изменение числовых данных задачи так, чтобы
появился новый способ решения или, наоборот,
чтобы один из способов решения стал невозможным.

46.

Способы проверки правильности
решения задачи
• составление задачи обратной данной и ее
решение;
• решение задачи другим способом;
• проверка правильности решения задачи по
всем условиям задачи;
• прикидка результата.

47.

Приёмы контроля и оценки:
формируемые умения
• сравнивать результат своей деятельности с
образцом, заданным в материальной или
графической форме;
• воспроизводить состав контрольных действий и
операций, заданных учителем;
• выполнять действие по развернутой инструкции;
• сличение результата деятельности с образцом на
основе самостоятельно прогнозируемых условий
эффективности;
• выполнение действий по общей инструкции;
• осуществление самопроверки;
• самостоятельное корректирование работы.

48.

Примеры дифференцированного обучения

49.

Схемы задач

50.

Составные задачи в начальном
курсе математики.
3 вопрос

51.

Виды типовых составных задач:
1 – Задачи на пропорциональное деление.
Задача: «С одного поля собрали 4 мешка
картофеля массой 192 кг. С другого – 6 таких
же мешков. Какова масса мешков с
картофелем, собранных с другого поля?»

52.

Виды типовых составных задач:
2 – Задачи на нахождение числа по двум
разностям.
Задача: С одного поля собрали 4 мешка
картофеля, со второго – 6 таких же мешков.
Масса всего собранного картофеля – 480 кг.
Какова масса картофеля собранного с каждого
поля?

53.

Виды типовых составных задач:
3 - Задачи на нахождение четвертого
пропорционального.
Задача: С одного поля собрали 4 мешка
картофеля, со второго – 6 таких же мешков.
Какова масса картофеля, собранного с
каждого поля, если со второго поля собрали
на 96 кг больше, чем с первого?

54.

Табличные модели задач на
пропорциональное деление
Задача. 40 кг печенья расфасовали в 5
одинаковых ящиков, сколько килограммов
печенья можно упаковать в 12 таких же
ящиков?

55.

Табличные модели задач на
пропорциональное деление
Задача: В одном хозяйстве для коров и лошадей
заготовили по одинаковому количеству центнеров
сена. Для коров в день расходуют 8 ц сена, а для
лошадей 4 ц сена. На сколько дней хватит
заготовленного сена коровам, если лошадям хватит
заготовленного сена на 200 дней?

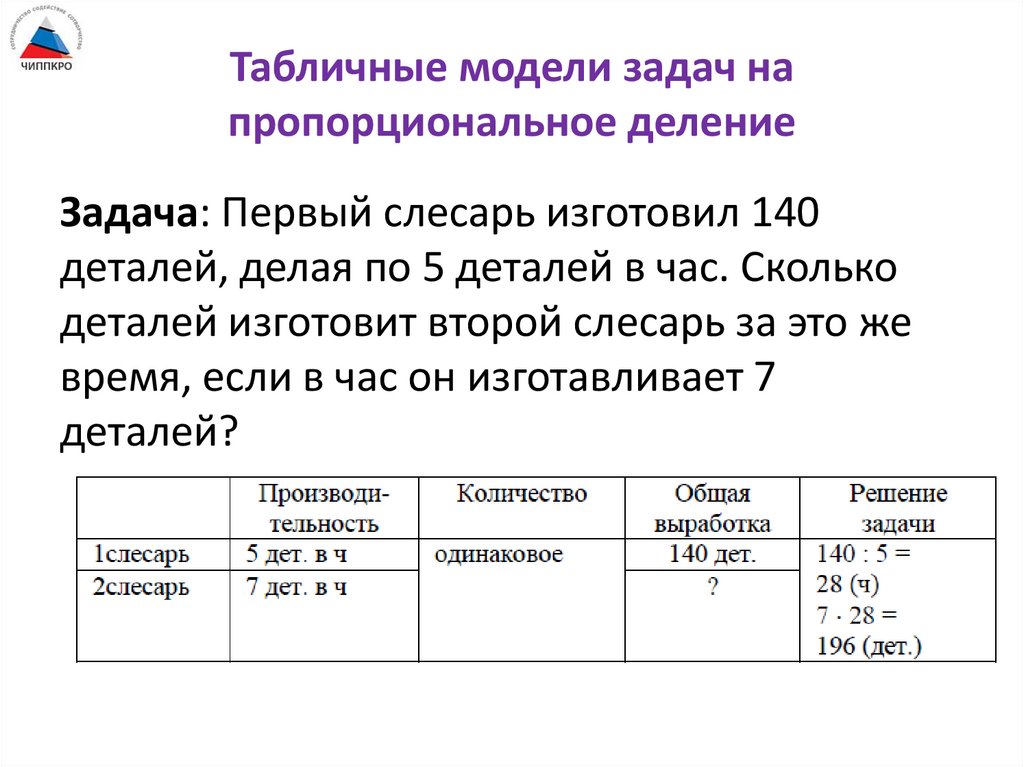
56.

Табличные модели задач на
пропорциональное деление
Задача: Первый слесарь изготовил 140
деталей, делая по 5 деталей в час. Сколько
деталей изготовит второй слесарь за это же
время, если в час он изготавливает 7
деталей?

57.

Составление задач по табличной модели
1)
2)

58.

3)
4)
5)

59.

Обучение решению задач на
движение

60.

Задачи на зависимость между
величинами
S
V
t
S
С
Ц
К
a
b

61.

Виды движения: задачи на встречное движение

62.

Виды движения: задачи на противоположное движение

63.

Виды движения: задачи на
однонаправленное (вдогонку) движение

64.

Этапы изучения задач на движение
Первый этап. Выделение объектов движения,
величин, характеризующих явление, введение
названия явления, актуализация слов, связанных с
движением.
Вводимые понятия: объекты движения, расстояние
или пройденный путь, скорость, время движения,
двигается быстрее, медленнее, догоняет, обгоняет,
удаляется, двигается навстречу, в противоположных
направлениях, вдогонку.
Начать реализацию этого этапа можно с экскурсии к
оживленному перекрестку или к месту, где можно
наблюдать движение объектов.

65.

Этапы изучения задач на движение
Второй этап: знакомство с моделированием разных
видов движения и единицами измерения величин.
Вводимые понятия: время сближения при
встречном движении.
Задача. Марина и Толя одновременно вышли
каждый из своего дома и направились в школу.
Через 15 минут они встретились в школе. Сколько
минут был в пути Толя? Сколько минут была в пути
Марина?

66.

Этапы изучения задач на движение
Задание 1. Ученики вышли из школы и направились домой.
Изобрази на чертеже возможные варианты их движения.
(Работаем с чертежом)
Задача 2. Расстояние между остановками автобусов 2 км. От
остановок отошли 2 автобуса, но в пути они остановились.
Один из них до момента остановки проехал 320 м, а другой –
380 м. На каком расстоянии друг от друга остановились
автобусы?
Задача 3. Марина и Толя одновременно вышли каждый из
своего дома и направились в школу. Через 15 минут они
встретились в школе. Сколько минут был в пути Толя? Сколько
минут была в пути Марина?
Задания такой структуры помогут учащимся осознать характерный признак
задач на встречное или противоположно направленное движение: одинаковое
время в пути для обоих сближающихся или удаляющихся объектов.

67.

Этапы изучения задач на движение
Третий этап: решение задач с использованием значений
одной величины.
Задание 1. Объясните смысл предложений.
Вертолет летит со скоростью 190 км в ч.
От города до садового поселка 82 километра.
Пчела в одну секунду пролетает около 7 метров.
Велосипедист был в пути 1 час 30 минут.
Задача 2. Пешеход проходит 4 км в ч, а велосипедист
проезжает в 3 раза больше. На сколько километров
больше за час проезжает велосипедист, чем проходит
пешеход?

68.

Этапы изучения задач на движение
Четвертый этап: решение простых задач на зависимость
между величинами.

69.

Этапы изучения задач на движение
Пятый этап – решение типовых задач на зависимость
между величинами V, t, S.
Задачи на нахождение четвертого
пропорционального.
Задача. Вертолет за 2 часа пролетел 340 км. До пункта
назначения ему осталось лететь еще 5 часов, если он
будет лететь с той же скоростью. Сколько километров
осталось пролететь вертолету до пункта назначения?

70.

Этапы изучения задач на движение
Задачи на пропорциональное движение.
Задача. Автотуристы в первый день были в пути 6 ч,
а во второй 4 часа. Всего они проехали 600 км.
Какое расстояние проезжали туристы каждый день,
если они ехали с одинаковой скоростью?

71.

Этапы изучения задач на движение
Задачи на нахождение числа по двум разностям
Задача. Два самолета летели с одинаковой
скоростью. Один самолет был в воздухе 4 часа,
другой - 6 часов. Первый самолет пролетел меньше
второго на 1400 км. Какое расстояние пролетел
каждый самолет?

72.

Этапы изучения задач на движение
Шестой этап: введение понятий «скорость
сближения» и «скорость удаления»

73.

Организация математического
образования в начальном
общем образовании
Девятова Ирина Евгеньевна,
доцент, кандидат педагогических наук,
доцент кафедры начального образования ЧИППКРО,
эксперт Учебно-методического объединения в сфере общего образования в
Челябинской области,
специалист, осуществляющий анализ профессиональной деятельности
педагогических работников на территории Челябинской области