Методика изучения длины в процесе изучения геометрического материала

1.

2.

ВВЕДЕНИЕ
К величинам относят длину, массу, время,
емкость (объём), площадь и др.
Все эти величины и единицы их измерения
изучаются в начальной школе.
Результатом процесса измерения величины
является определенное численное значение,
показывающее сколько раз выбранная мера
«уложилась» в измеряемую величину.

3.

В начальной школе рассматриваются только
такие величины, результат измерения
которых выражается целым положительным
числом (натуральным числом).
В связи с этим процесс знакомства ре6енка с
величинами и их мерами рассматривается в
методике как спосо6 расширения
представлений ре6енка о роли и
возможностях натуральных чисел.

4.

В процессе измерения различных величин
ребенок упражняется не только в действиях
измерения, но и получает новое
представление о неизвестной ему ранее роли
натурального числа.
Число - это мера величины и сама идея числа
6ыла в 6ольшой мере порождена
нео6ходимостью количественной оценки
процесса измерения величин.

5.

ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
С давних пор люди сталкивались с необходимостью
определять расстояния, длины предметов, время,
площади, объемы и т. д.
Измерения нужны были и в строительстве, и в
торговле, и в астрономии, фактически в любой
сфере жизни. Очень большая точность измерений
нужна была при строительстве египетских пирамид.

6.

Значение измерений возрастало по мере
развития общества и, в частности, по
мере развития науки. А чтобы измерять,
необходимо было придумать единицы
различных
физических
величин.
Вспомним, как написано в учебнике:
“Измерить какую-нибудь величину –
это значит сравнить ее с однородной
величиной, принятой за единицу этой
величины”.

7.

Самыми древними единицами были
субъективные единицы. Так, например,
моряки измеряли путь трубками, т. е.
расстоянием, которое проходит судно
за время, пока моряк выкурит трубку.

8.

В Испании похожей единицей была
сигара, в Японии – лошадиный
башмак, т. е. путь, который
проходила
лошадь,
пока
не
износится привязанная к ее копытам
соломенная подошва, заменявшая
подкову.

9.

В программе Олимпийских игр Древней
Эллады был бег на стадию. Установлено,
что греческая стадия (или стадий) это
длина стадиона в Олимпии – 192,27 м.
Стадий равняется расстоянию, которое
проходит человек спокойным шагом за
время от появления первого луча солнца,
при его восходе, до момента, когда диск
солнца целиком окажется над горизонтом.
Это время приблизительно равно двум
минутам...

10.

Стадий, как единица измерения расстояний,
был и у римлян (185 см), и у вавилонян (около
195 см), и у египтян (195 см).
В Сибири в стародавние времена употреблялась
мера расстояний – бука. Это расстояние, на
котором человек перестает видеть раздельно
рога быка.

11.

У многих народов для определения расстояния
использовалась единица длины стрела –
дальность полета стрелы. Наши выражения “не
подпускать на ружейный выстрел”, позднее “на
пушечный выстрел” – напоминают о подобных
единицах длины.

12.

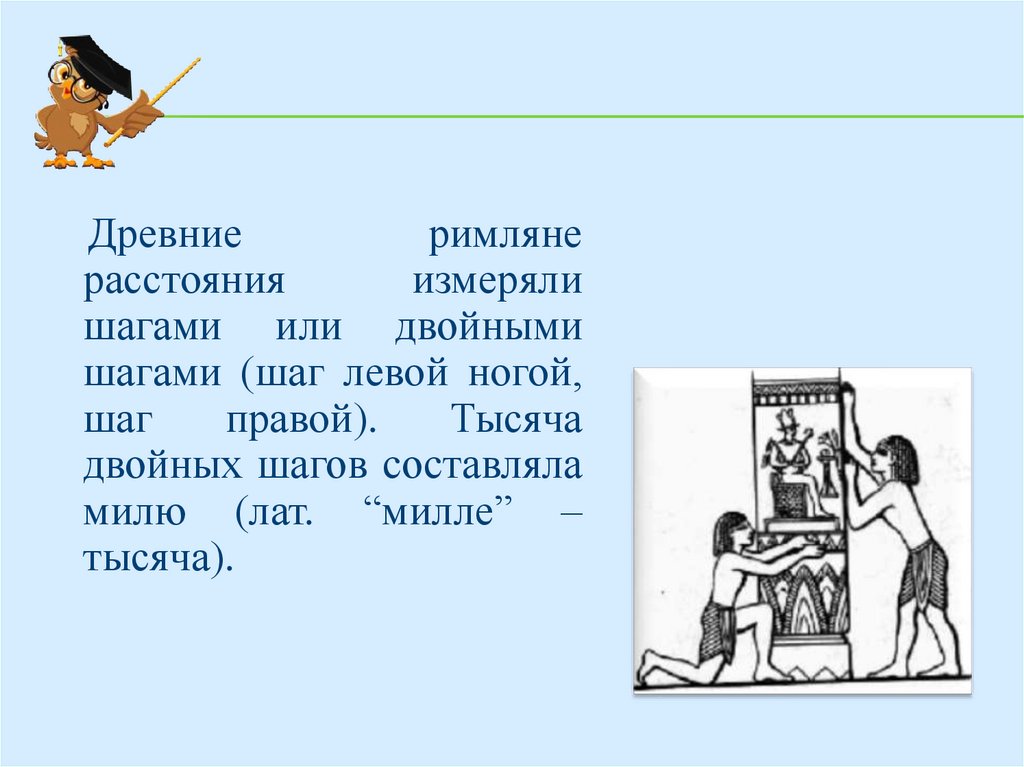
Древние
римляне
расстояния
измеряли
шагами или двойными
шагами (шаг левой ногой,
шаг
правой).
Тысяча
двойных шагов составляла
милю (лат. “милле” –
тысяча).

13.

Длину веревки или ткани неудобно измерять
шагами или стадиями. Для этого оказались
пригодными встречающиеся у многих народов
единицы, отождествляемые с названиями
частей человеческого тела.

14.

Локоть – расстояние от
конца пальцев до
локтевого сустава.

15.

Мерой длины для тканей, веревок и т.п.
наматывающихся материалов у многих народов
был двойной локоть. Этой мерой мы и сейчас
пользуемся для приблизительной оценки
длины.
На Руси долгое время в качестве единицы
длины использовали аршин (примерно 71 см).
Эта мера возникла при торговле с восточными
странами
(перс,
“арш”
–
локоть).
Многочисленные выражения: “Словно аршин
проглотил”, “Мерить на свой аршин” и другие –
свидетельствуют о ее распространении.

16.

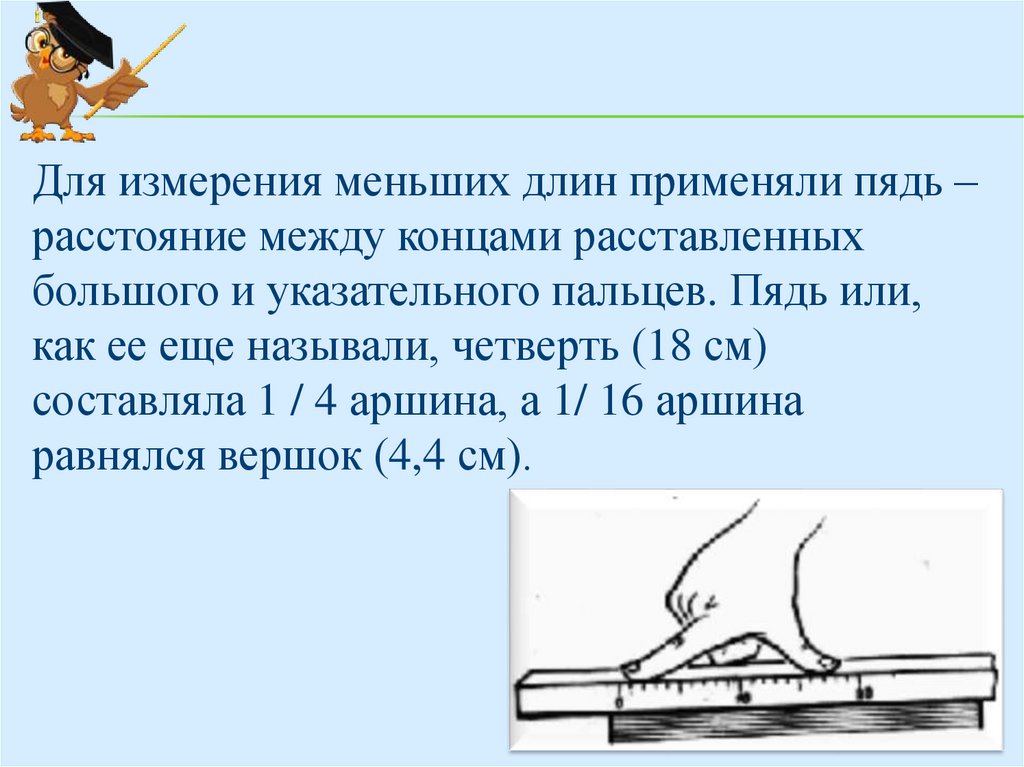
Для измерения меньших длин применяли пядь –
расстояние между концами расставленных
большого и указательного пальцев. Пядь или,
как ее еще называли, четверть (18 см)
составляла 1 / 4 аршина, а 1/ 16 аршина
равнялся вершок (4,4 см).

17.

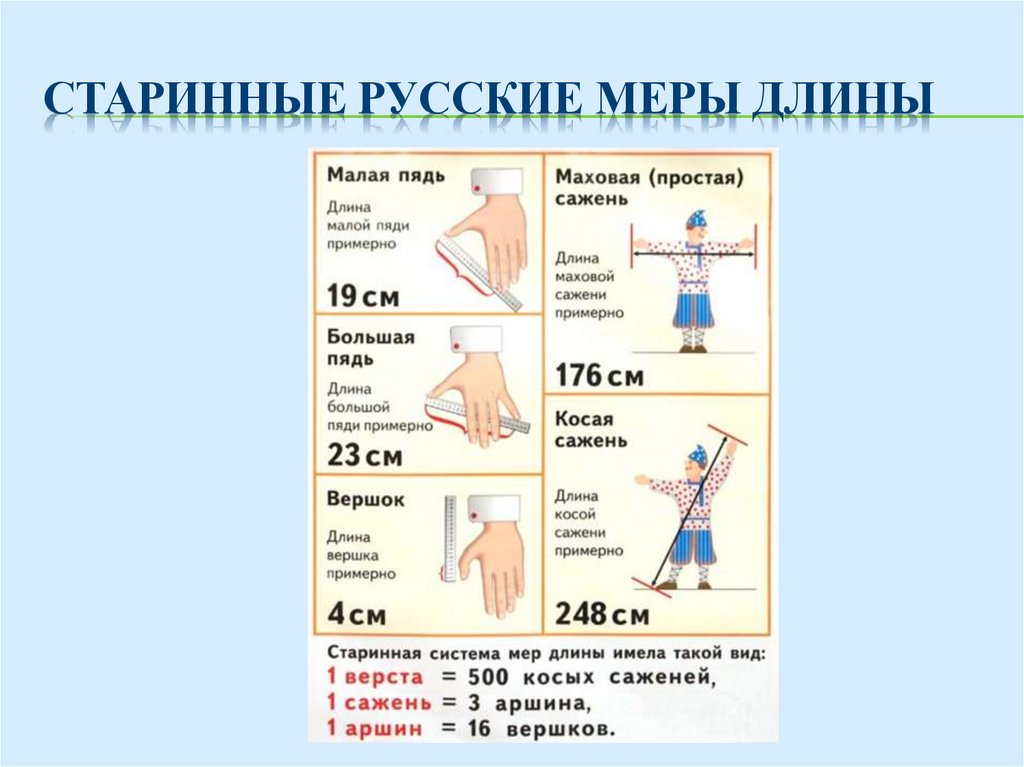
Очень распространенной единицей длины
была сажень. Впервые упоминание о ней
встречается в XI в. С 1554 г. сажень
устанавливают равной 3 аршинам (2,13 м)
и она получает название царской (или
орленой, печатной) в отличие от
произвольных – маховой и косой.
Маховая сажень – размах рук – равна
примерно 2,5 аршинам. Рыбак, который
показывает, какую большую рыбу он
упустил, демонстрирует нам маховую.

18.

Косая
сажень
–
расстояние от конца
вытянутой
вверх
правой руки до носка
левой
ноги,
она
примерно равна 3,25
аршинам.

19.

Вспомним, как в сказках о великанах: “Косая сажень в
плечах”. Удивительно совпадение древнеримской меры
длины - "архитектурной трости" и древнерусской косой
сажени: 248 см. Имеется в виду сажень "с ноги на руку
косая, от земли и до земли". Эту сажень определяли
длиной веревки, один конец которой прижимался ногой
к земле, а другой перекидывался через согнутую в
локте руку стоящего человека и опускался снова до
земли.
При сложении упомянутой выше косой сажени
вчетверо получаем "литовский локоть" (62 см).

20.

В странах Западной Европы издавна применяли
в качестве единиц дюйм (2,54 см) –длина
сустава большого пальца (от голл. “дюйм” –
большой палец) и фут (30 см) – средняя длина
ступни человека (от англ. “фут” – ступня).

21.

Для измерения больших расстояний на Руси
использовали единицу поприще, замененной позже
верстой (в разных местностях версту считал по-С
конца 18 в., до введения метрической системы мер,
1 верста= 500 caженям = 1,0668 км
А как же измерялись на Руси большие расстояния?
В этом случае люди говорили, что расстояние от
Санкт-Петербурга до Москвы три дня пути.
разному- от 500 до 750 сажен.)

22.

Локоть, вершок, пядь, сажень, дюйм, фут
и т. д. очень удобны при измерениях, так
как они всегда “под руками”. Но единицы
длины,
соответствующие
частям
человеческого тела, обладают большим
недостатком: у различных людей пальцы,
ступни и т. д. имеют разную длину. Чтобы
избавиться от произвола, в XIV в.
субъективные единицы начинают заменять
набором объективных единиц.

23.

Так, например, в 1324 г. в Англии был
установлен законный дюйм, равный длине трех
приставленных друг к другу ячменных зерен,
вытянутых из средней части колоса . Фут
определили как среднюю длину ступни
шестнадцати человек, выходящих из церкви, т.
е. обмером случайных людей стремились
получить более постоянное значение единицы –
среднюю длину ступни.

24.

В 1791 г. во Франции было принято решение
создать десятичную метрическую систему мер.
Основными величинами в этой системе были выбраны
длина и масса.
Комиссия, в которую входили крупнейшие
французские ученые, предложила принять за единицу
длины 1/40000000 часть длины земного меридиана,
проходящего через Париж. Измерить длину меридиана
было поручено астрономам Мешену и Деламберу.
Работа продолжалась шесть лет. Ученые измерили часть
длины меридиана, расположенную между городами
Дюнкерком и Барселоной, а затем вычислили полную
длину четверти меридиана от полюса до экватора.

25.

На основании их данных
из
платины
был
изготовлен эталон новой
единицы. Эту единицу
назвали метром – от
греческого
слова
“метрон”, что значит
“мера”

26.

Метрическая система мер
принята большинством
стран мира. В России ее
введение началось с 1899
года. Большие заслуги во
введении и распространении
метрической системы мер в
нашей стране принадлежит
Дмитрию Ивановичу
Менделееву, великому
русскому химику.

27.

С давних пор люди сталкивались с
необходимостью определять расстояния,
длины предметов.
Измерения нужны были и в строительстве, и в
торговле, и в астрономии, фактически в любой
сфере жизни. Очень большая точность
измерений нужна была при строительстве
египетских пирамид.

28.

СТАРИННЫЕ РУССКИЕ МЕРЫ ДЛИНЫ

29.

ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДИКИ
ИЗУЧЕНИЯ ДЛИНЫ МЛАДШИМИ
ШКОЛЬНИКАМИ
Знание мер длины, умение находить
длину, ширину, высоту и т. п. необходимы
учащимся и в быту, и при овладении
профессией. Со всеми мерами длины и их
соотношениями учащиеся начальной школы
знакомятся в течение всего времени
обучения в младших классах, закрепление
же этих мер проходит в течение всех лет
обучения в школе.

30.

Знакомство с понятиями длинный - короткий,
широкий - узкий, высокий - низкий учащиеся
получают еще в дошкольный период, коррекция
этих понятий осуществляется в дочисловой
период. К сожалению, многие дети, приходя из
детского сада, считают, что длина, ширина и
высота это разные величины.

31.

ПЛАН ИЗУЧЕНИЯ ТЕМЫ И ВРЕМЯ
ВВЕДЕНИЯ (УМК «ШКОЛА РОССИИ»)
1 класс
Понятие длины как
свойства
предметов
(М1М1 с.32).
Прямая и кривая
линии(М1М1 с.40).

32.

Отрезок.
Сравнение
отрезков
(М1М1 с.40)

33.

Сантиметр
(М1М1 с.66)

34.

Дециметр
(М1М2 с.51)

35.

2 КЛАСС
Миллиметр
(М2М1 с.10)

36.

Метр
(М2М1 с.13)

37.

Длина ломанной
(М2М1 с.32)

38.

Периметр
многоугольника
(М2М1 с.42)

39.

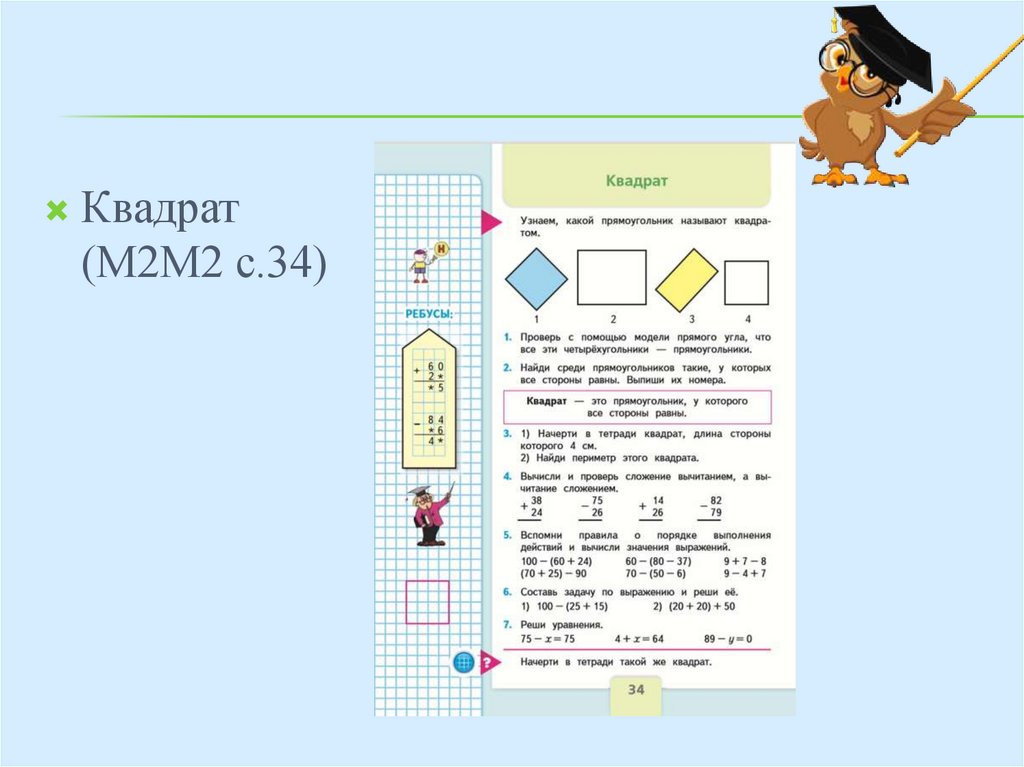
Квадрат
(М2М2 с.34)

40.

3 КЛАСС
Окружность
(М3М1 с.94)

41.

Виды треугольников
(М3М2 с.73)

42.

4 КЛАСС
Величины
(Единицы длины)
(М4М1 с.36-37)

43.

ЗАДАЧИ ИЗУЧЕНИЯ ТЕМЫ
1.Сформировать понятие длины как
свойства предметов.
2.Познакомить с единицами длины и
соотношениями между ними.
3.Сформировать умения измерять
длину данных отрезков и чертить
отрезки заданной длины, сравнивать
длины.
4.Научить выражать величины в
меньших и больших единицах.
5.Научить выполнять действия над
величинами устно и в столбик.

44.

ДЛИНА ПРЕДМЕТА
1 ЭТАП:
опираемся на жизненный опыт
детей и вводим понятие «длина
предмета». До этого урока с
первых уроков в 1 классе дети
сравнивали предметы по размеру
или по величине. На этом уроке
уточняем и вводим новое понятие
«сравнение по длине». Для этого
к доске прикрепляем различные
картинки с предметами, которые
будем сравнивать по размеру.

45.

2 ЭТАП
Цель: научить сравнивать предметы
по длине разными способами.
Этот этап начинается сразу на первым
же уроке.
А) прежде всего детей знакомят со
способом сравнения длин «на глаз» .
Предлагаем предметы контрастные по
размеру
и просим правильно
сформулировать результаты, используя
термин длина. (Длина карандаша
меньше длины парты и т.д.)
Б) создаем проблемную ситуацию, в
которой показываем, что первый
способ не всегда удобен.

46.

3 ЭТАП.
Цель: ввести единую единицу измерения
длины и измерительный прибор.
Перед
введением
рассматриваем
проблемную
ситуацию,
в
которой
подчеркиваем, что в жизни использовать
разные мерки для измерения длины
неудобно. Можно рассказать о различных
мерах
длины
на
Руси,
например,
использовали локоть. Неудобно, т.к. локоть у
разных людей имеет разную длину.
Следовательно, нужны единые меры длины и
в
середине
19
века
появляется
Международная система измерения (СИ).
Первой единицей измерения, которую
вводят в 1 классе, является сантиметр (см).
Пишут это слово на доске и показывают
наименование СМ (без точки). Выдаем
мерки в 1 см и полоски, которые будет
измерять ученик. Сравниваем мерку с
длиной клеток и убеждается, что в 1 см 2
клетки. М1М1 с.66.

47.

ДАЛЕЕ ВЫПОЛНЯЕМ УПРАЖНЕНИЯ ПО
ИЗМЕРЕНИЮ ДЛИН В САНТИМЕТРАХ:
1. Закрываем всю полоску моделями см , нужно узнать сколько см укладывается в отрезке.
2. Предлагаем полоску, для измерения которой не хватает моделей мерок, тогда используем
одну мерку и ставим отметки. Такой способ неудобен. Подводим к введению линейки.
3. Сначала используют «самодельную» линейку. Для ее изготовления детям выдают полоску из
картона длиной 10 см, но дети этого не знают. Предлагаем детям определить длину полоски в
см, для этого используем модель см – мерку. Дети ставят отметки, а затем просим
пронумеровать эти отметки.
М1М1 стр.66
1
2
3
4
5
6
7
8
9
10
Теперь, чтобы узнать длину любой полоски, прикладываем первую расчерченную полоску к
новой так, чтобы левые концы совпали, и смотрим напротив какого деления находится
правый конец новой полоски. Сообщаем, что мы изготовили прибор для измерения длин
отрезков - линейку .

48.

4 ЭТАП
Сложение и вычитание
величин, выраженных в
см. Задания типа: длина
синей полоски 6 см, а
красной на 3 см больше.
Какова длина красной ?
решение : 6 см +3 см = 9
см

49.

5 ЭТАП
Ознакомление с другими единицами измерения
длины.
Этот этап длительный. С первого по четвертый
класс постепенно
вводят другие единицы измерения: мм, дм, км.
Каждый раз при введении создают проблемную
ситуацию, показывающую, что уже известные
единицы измерения
неудобны в данной
ситуации, следовательно, нужна новая.
При введении мм предлагаем измерять длину
отрезка,
меньше одного сантиметра. При
введении км проводим урок на улице. Для этого
выходят в парк. Учитель должен приблизительно
показать расстояние в один км. От…и до…
Хорошо, если установлены метки. Шаг ребенка
приблизительно 30 см, а взрослого 50см. Чтобы
преодолеть метр, нужно сделать 3 ребенку или 2
шага
взрослому.
Предлагаем
пройти
определенное расстояние, считая свои шаги.
Сосчитать сколько шагов взрослого и ребенка в
одном км.

50.

Изучая
различные
единицы
измерения, особое
внимание уделяют
соотношению между ними.
М4М1 с. 36
1км = 1000м
1м = 10дм
1дм = 10см
1см = 10мм
На этом этапе предлагают задания
на перевод из
одной единицы измерения
в другую.

51.

М4М1 с. 36-37.
При переводе из более
крупных мер в более
мелкие
выполняют
умножение.
3 км=3000м
При переводе из мелких
в крупные – деление.
3000м=3км

52.

6 ЭТАП
Сложение
и
вычитание
величин,
выраженных
в
единицах
двух
наименований.
М4М1 с. 67 . Случаи без перехода через
меру рассматривают устно. С переходом письменно в столбик.
А) 2м 45см + 3м 15см = 5м 60см (устно).
Такие вычисления проводят без перевода из
одной меры в другую.
Б) Письменный случай требует перевода в
более мелкую меру.
124м 75см + 39м 85см = 164м 60см
124м 75см = 12475см
39м 85см = 3985см
12475
+
3985
16460
16460см=164м60см
Дают упражнения на закрепление.

53.

7 ЭТАП
Умножение и деление величины на
число. М4М1 с. 77
А) Устный случай: 2м 15см * 3 = 6м
45см. делают устно в строчку.
Б) Письменный случай с переводом
в более мелкую меру.
4 км 750м * 5 = 23км 750м
4км 750м = 4750м
4750
*
5
23750
23750м=23км750м

54.

СВОДНАЯ ТАБЛИЦА СООТНОШЕНИЙ
МЕЖДУ ВСЕМИ ЕДИНИЦАМИ ДЛИНЫ

55.

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ПРОГРАММ
РАЗВИВАЮЩЕГО ОБУЧЕНИЯ Л.Г. ПЕТЕРСОН И
ПРОГРАММЫ ТРАДИЦИОННОГО ОБУЧЕНИЯ
М.И. МОРО

56.

ПРОГРАММА Л.Г. ПЕТЕРСОН
Понятие величины в начальном курсе математики не
определяется, то есть даётся без определения. Данное
понятие раскрывается на конкретных примерах и
основывается на опыте ребёнка. Величины в
начальном курсе математики рассматриваются как
свойство предметов или явлений, проявляющееся в
результате сравнения. Особенно явно это проявляется в
традиционной программе Л.Г. Петерсон.

57.

Изучение величин в первом
классе
по
программе
Петерсон Л.Г. начинается с
изучения отрезка и его
частей. На этом этапе дети
учатся правильно измерять
отрезки, чертить отрезки
заданной длины, то есть
приобретают измерительные
умения. (М1П2 с.1)

58.

На следующем этапе
изучается тема "Длина".
Здесь дети измеряют
отрезки с помощью
различных мерок, вводится
первая единица измерения
длины - сантиметр.
(М1П3 с.1)

59.

Далее
изучается
свойства величин.
Отрезки
сравниваются
по
длине.
(М1П3 с.14)

60.

На следующем этапе
учащиеся
изучают
новую
единицу
измерения
длины
дециметр. Дети узнают
соотношение
между
двумя
изученными
единицами
длины:
сантиметром
и
дециметром.
(М1П3 с.52)

61.

Во втором классе дети
изучают
метр,
соотношение изученных
единиц
длины:
сантиметр,
дециметр,
метр. Учатся выражать
численные
значения
величин в различных
единицах
измерения.
(М2П1 с.36)

62.

Далее изучают длину
ломанной и периметр.
(М2П2 с.3)

63.

Затем
учащиеся
знакомятся
с
единицами
площади.
(М2П2 с.43)

64.

Площадь
прямоугольника
(М2П2 с.56)

65.

Единицы объёма
(М2П3 с.41)

66.

На следующем этапе
изучаются
новые
единицы
измерения
длины - миллиметр и
километр. Здесь дети
выясняют, для чего
используют
такую
мелкую
(крупную)
мерку.
(М2П3 с.63)

67.

Соотношения между
единицами длины
(М2П3 с.64)

68.

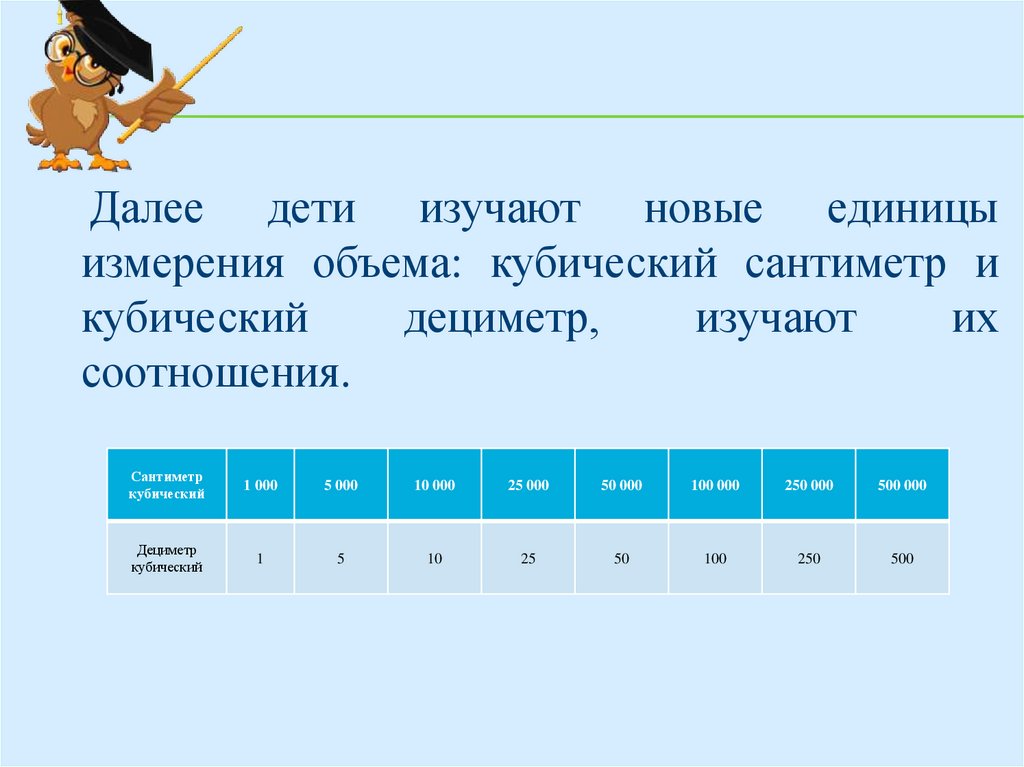
Далее дети изучают новые единицы
измерения объема: кубический сантиметр и
кубический
дециметр,
изучают
их
соотношения.
Сантиметр
кубический
1 000
5 000
10 000
25 000
50 000
100 000
250 000
500 000
Дециметр
кубический
1
5
10
25
50
100
250
500

69.

В третьем классе
начинается работа с
единицами длины
(М3П1 с.5)

70.

Так же как и площадь
прямоугольника, дети
изучают
объем
прямоугольного
параллепипеда.
(М3П2 с.89)
.

71.

На следующем этапе
дети изучают площадь
прямоугольного
прямоугольника. Здесь
учащиеся знакомятся с
формулой вычисления
площади
прямоугольного
треугольника.
(М4П1 с.94-95)

72.

В дальнейшем дети
изучают
новые
единицы измерения
площади:
ар
и
гектар.
(М4П2 с.125-126)

73.

ПРОГРАММА "ШКОЛА РОССИИ" М.И МОРО
Изучение величин в первом классе по
программе "Школа России" М.И Моро
начинается с изучения отрезка и его частей.
На этом этапе дети учатся правильно измерять
отрезки, чертить отрезки заданной длины, т.е.
приобретают измерительные умения.

74.

На следующем этапе изучается тема "Длина".
Здесь дети измеряют отрезки с помощью
различных мерок, вводится первая единица
измерения длины - сантиметр.

75.

На следующем этапе дети изучают новую
единицу измерения длины - дециметр. Дети
изучают
соотношение
между
двумя
изученными единицами длины: сантиметром и
дециметром.

76.

Во втором классе дети изучают миллиметр и
метр, соотношение изучаемых единиц длины.
Учатся выражать численные значения величин
в различных единицах измерения, переводят
мелкие единицы в более крупные и наоборот.

77.

Изучение
величин
в
третьем классе начинается
с
изучения
площади:
квадратный
сантиметр,
квадратный
дециметр,
квадратный
метр.
На
данном
этапе
дети
измеряют площадь фигуры
различными
мерками,
сравнивают
численные
значения площадей фигур,
измеренных различными
мерками.

78.

В четвертом классе учащиеся знакомятся с
новой единицей длины - километром. Здесь
дети выясняют, для чего используют такую
крупную мерку. Выполняют упражнения на
соотношение единиц длины.

79.

На следующее этапе изучаются новые
единицы измерения площади - квадратный
километр и квадратный миллиметр. Дети
учатся находить площадь фигуры с помощью
палетки.

80.

СРАВНЕНИЕ ИЗУЧЕНИЯ ВЕЛИЧИН ПО
ПРОГРАММЕ РАЗВИВАЮЩЕГО ОБУЧЕНИЯ Л.Г.
ПЕТЕРСОН И ПО ПРОГРАММЕ ТРАДИЦИОННОГО
ОБУЧЕНИЯ М.И. МОРО"
По традиционной программе большее
внимание
уделяется
изучению
натурального ряда чисел, а уже на
втором месте идёт изучение величин; в
программе
развивающего
обучения
предусмотрено рассмотрение основных
величин, их свойств и отношений между
ними с тем, чтобы показать, что числа,
их свойства и действия, производимые
над ними, выступают в качестве частных
случаев
уже
известных
общих
закономерностей величин.

81.

ЗАКЛЮЧЕНИЕ
Для более успешного изучения длины на уроках
математики в начальных классах, целесообразно
использовать развивающие упражнения.
Постановка проблемных заданий и
использование развивающих упражнений
улучшают качество знаний обучающихся,
способствуя развитию умственных действий
школьников.

82.

СПАСИБО ЗА ВНИМАНИЕ!