Задачи на построение

1.

2.

В геометрии выделяют задачи на построение,
которые можно решить только с помощью двух
инструментов: циркуля и линейки без масштабных
делений.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки;
с помощью циркуля можно провести окружность
произвольного радиуса, а также окружность с
центром в данной точке и радиусом, равным
данному отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

3. План решения задачи на построение.

• Анализ ( нахождение связи между
элементами геометрической фигуры).
Построение с обязательным описанием
хода его выполнения.
Доказательство получения искомой
фигуры.

4.

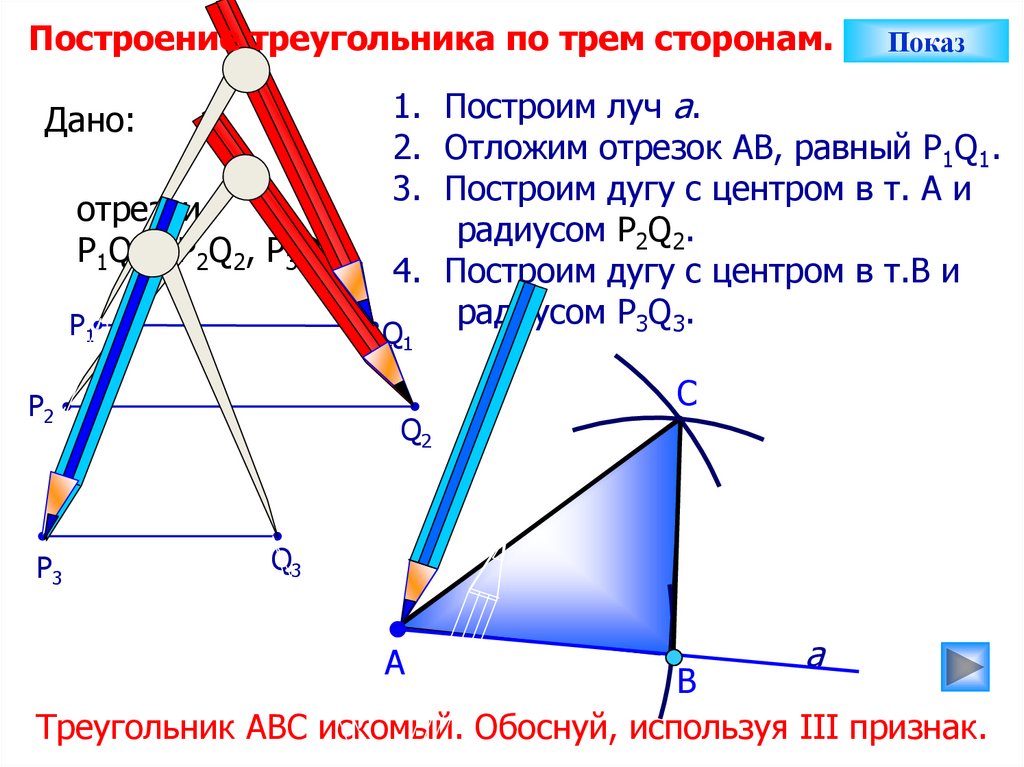
Построение треугольника по трем сторонам.
Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
P1
1. Построим луч а.
2. Отложим отрезок АВ, равный P1Q1.
3. Построим дугу с центром в т. А и
радиусом Р2Q2.
4. Построим дугу с центром в т.В и
радиусом P3Q3.
Q1
P2
P3
Показ
Q2
С
Q3
А
а
В
Треугольник АВС искомый. Обоснуй, используя III признак.

5.

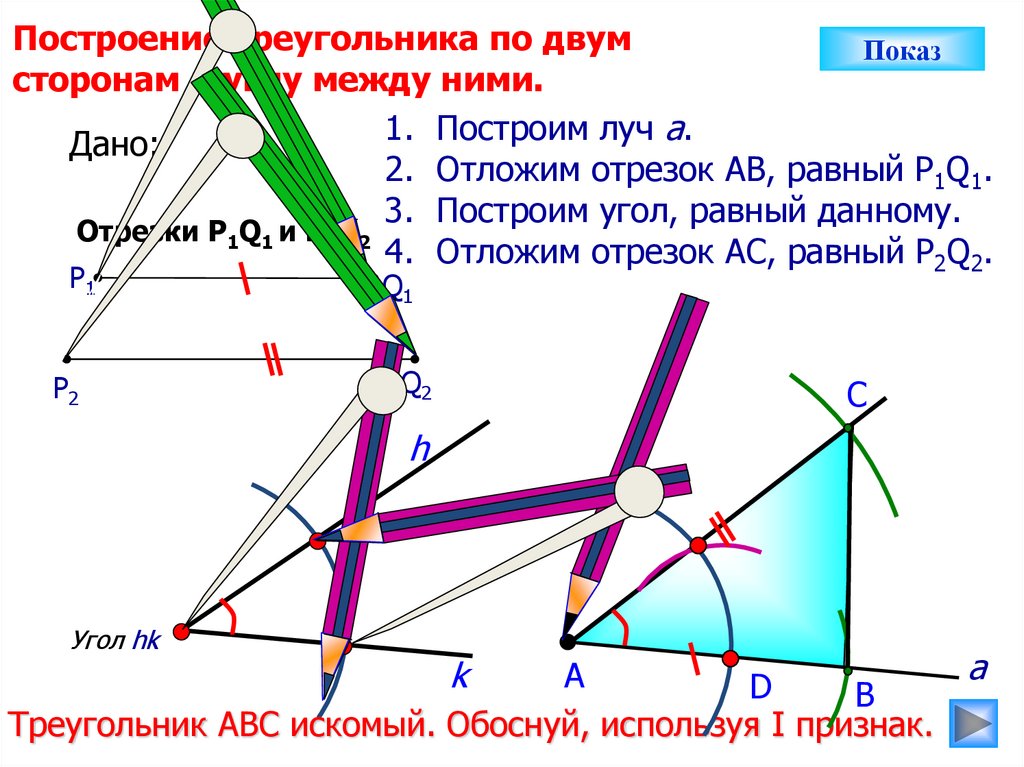
Построение треугольника по двум
Показ
сторонам и углу между ними.
1. Построим луч а.
Дано:
2. Отложим отрезок АВ, равный P1Q1.
3. Построим угол, равный данному.
Отрезки Р1Q1 и Р2Q2
4. Отложим отрезок АС, равный P2Q2.
P1
P2
Q1
Q2
С
h
Угол hk
а
А
D
В
Треугольник АВС искомый. Обоснуй, используя I признак.
k

6.

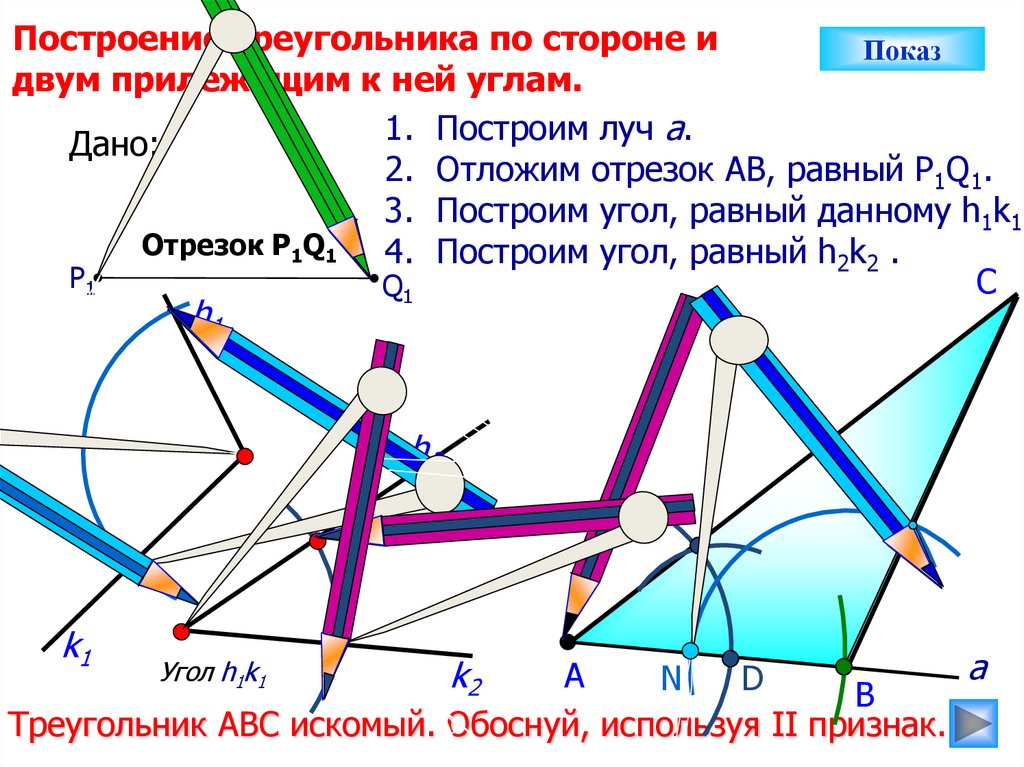
Построение треугольника по стороне и
Показ
двум прилежащим к ней углам.
1. Построим луч а.
Дано:
2. Отложим отрезок АВ, равный P1Q1.
3. Построим угол, равный данному h1k1.
Отрезок Р1Q1
4. Построим угол, равный h2k2 .
P1
С
Q1
h1
h2
k1
а
А
N
D
В
Треугольник АВС искомый. Обоснуй, используя II признак.
Угол h1k1
k2

7. НЕРАЗРЕШИМЫЕ ЗАДАЧИ

• ТРИСЕКЦИЯ УГЛА – деление данного угла
на три равных части с помощью циркуля и
линейки.

8. Учебные задания:

Постройте прямоугольный треугольник:
а) по двум катетам;
б) по катету и противолежащему острому
углу;
в) по гипотенузе и острому углу.