Вычисление значения опорной функции h(t) в i-й момент времени

1.

Вычисление значения опорной
функции h(t) в i-й момент времени
Вычисление приращений Dy, Du и
управлений u в i-й момент времени
Проверка
Umin<u<Umax
Выполнение
процедуры
ограничения
управлений
нет
да
Решение исходной динамической системы
Запоминание
параметров
траектории
Вычисление фазовых координат
в i+1-й момент времени
Контроль расстояния d >dогр
Реализация “посадки” на ПО
d = 0, d = 0, j (x) = 0
нет
да
Реализация схемы
движения по границе
поверхности j(x)=0,
нет
N , x 2
N , x 2
Краевая задача решена
i+1
Контроль
условий схода с
поверхности
да
нет
да
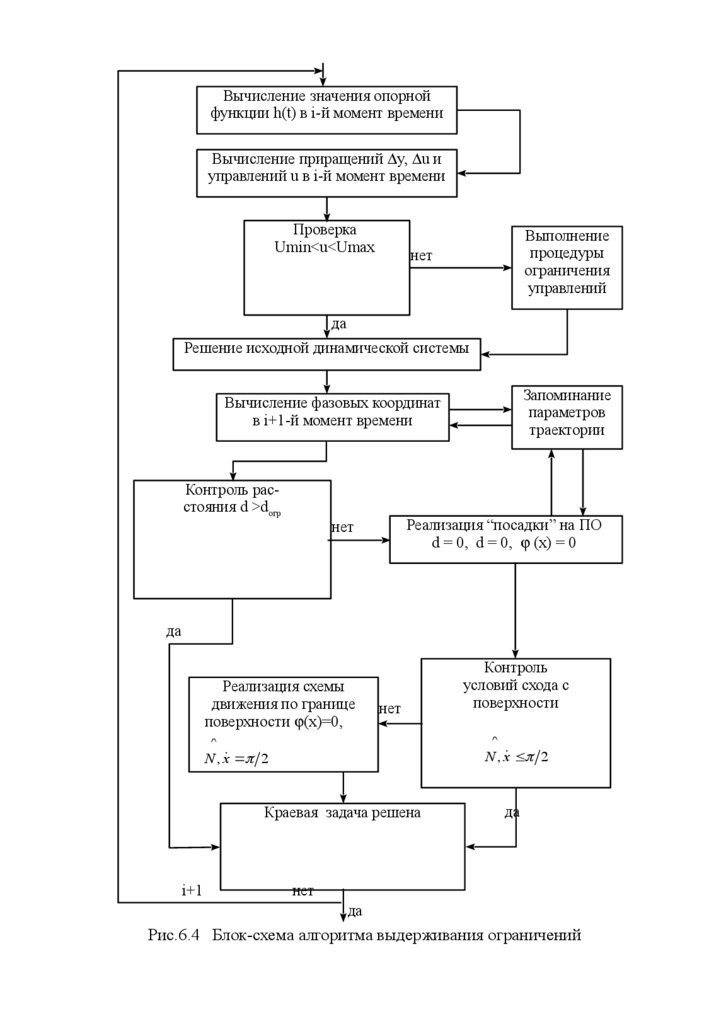
Рис.6.4 Блок-схема алгоритма выдерживания ограничений

2.

Начальные краевые условия:
x0, y0, u0, t0; xk, yk, uk, tk.
Краевые условия
в i-й момент
времени: xi, yi, ui, ti
Вычисление значений
опорной функции h(t)
в i-й момент времени
Вычисление приращений
Вычисление приращений
Dyik, Duik
Dyki, Duki
в i-й момент времени
в i-й момент времени
Вычисление управлений
ui+1 в i+1-й момент времени
Проверка
Umin<u<Umax
нет
ti+1
Выполнение
процедуры
ограничения
управлений
да
Решение исходной динамической системы
Вычисление фазовых координат
в i+1-й момент времени
Новые значения нет
Проверка
условия ti+1>tk
xi+1, yi+1, ui+1, ti+1
Запоминание
параметров
траектории
Проверка ограничений
на фазовые координаты
нет
да
Краевая задача решена
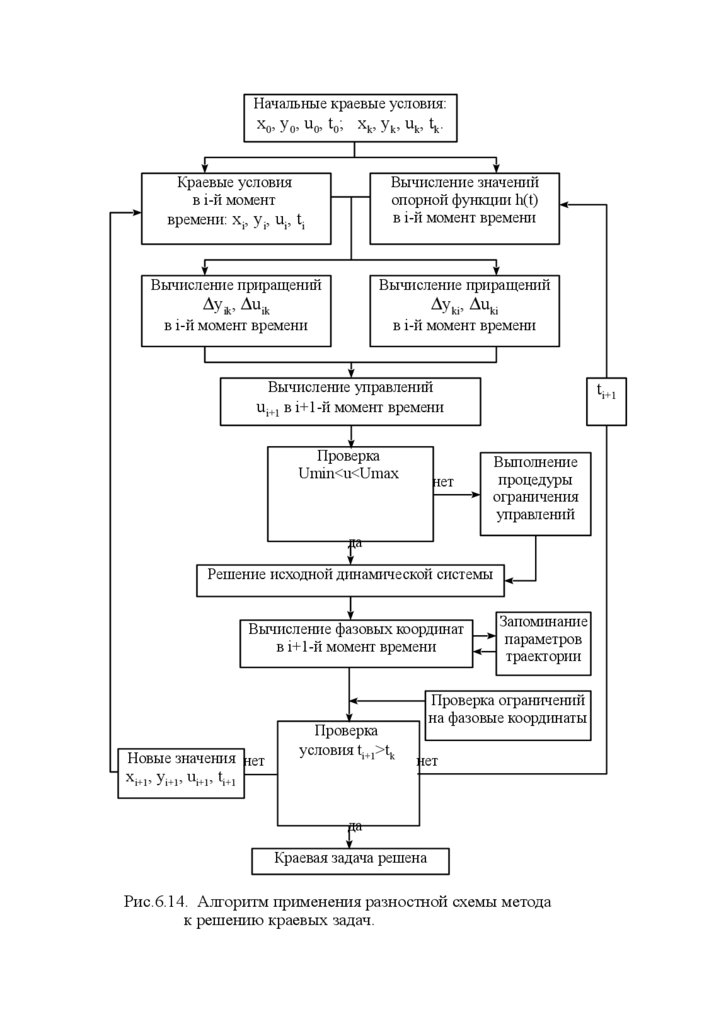
Рис.6.14. Алгоритм применения разностной схемы метода
к решению краевых задач.

3.

Начальные краевые условия:
x0, y0, u0, t0; xk, yk, uk, tk.
Краевые условия
в i-й момент
времени: xi, yi, ui, ti
Вычисление значений
опорной функции h(t)
в i-й момент времени
Вычисление приращений
Вычисление приращений
Dyik, Duik
Dyki, Duki
в i-й момент времени
в i-й момент времени
Вычисление управлений
ui+1 в i+1-й момент времени
Проверка
Umin<u<Umax
ti+1
Выполнение
процедуры
ограничения
управлений
нет
да
Решение исходной динамической системы
Запоминание
параметров
траектории
Вычисление фазовых координат
в i+1-й момент времени
Новые значения нет
xi+1, yi+1, ui+1, ti+1
Проверка
условия ti+1>tk
Проверка ограничений
на фазовые координаты
нет
да
Краевая задача решена
нет
Проверка
на:єg(h)є< e нет
G( h ) > 0
Пересчет параметров
функции
интенсивности
h=(h1, h2,....hp)
да
Задача оптимального управления решена
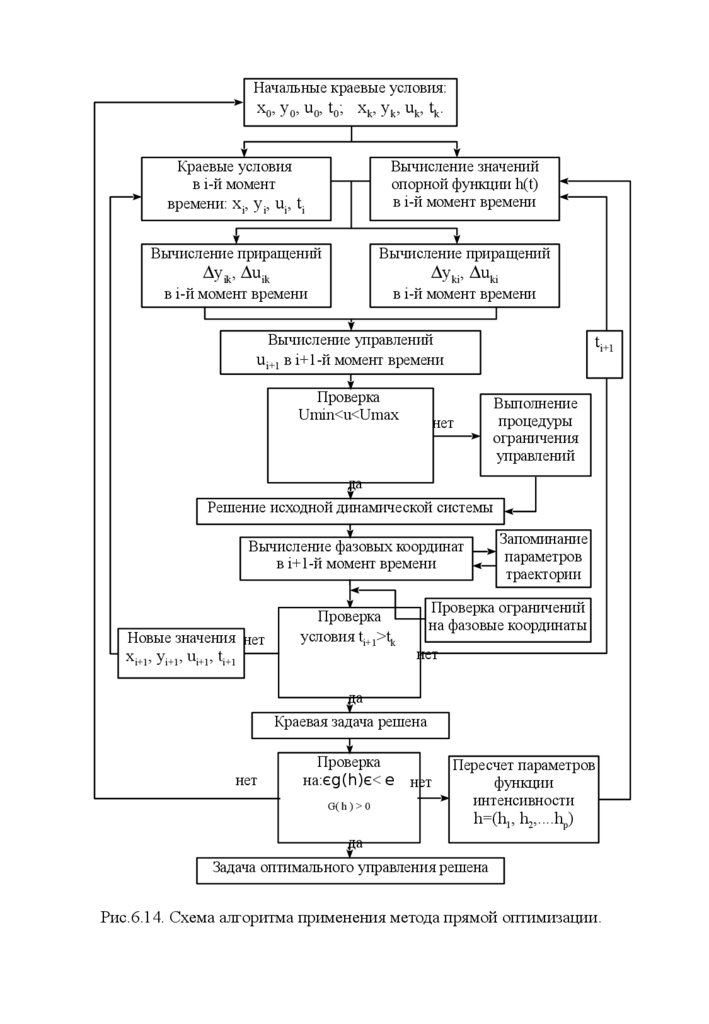
Рис.6.14. Схема алгоритма применения метода прямой оптимизации.