Функции.многих переменных

1.

Функции многих
переменных

2.

Определение функции двух переменных
Пусть D - некоторое множество упорядоченных
пар чисел ( x, y ) . Если каждой такой паре ( x, y ) D
по некоторому правилу ставится в соответствие
число z , то говорят, что на множестве D задана
функция двух переменных z f ( x, y ).
• Множество D
называется областью
определения функции.
• Так как каждую пару чисел ( x, y )
можно
отождествить с точкой M ( x, y )
на координатной
плоскости, то можно говорить, что функция z f ( x, y ).
задана на множестве D точек на плоскости.
2

3.

График функции
• Множество точек в пространстве
( x, y, f ( x, y )), ( x, y ) D
называется графиком функции z f ( x, y ).
• Пример. z 1 x 2 y 2
2
2
2
2
1
x
y
0
x
y
1
• Область определения
• круг радиуса 1. График – полусфера z 0 радиуса 1.
z
( x, y, f ( x, y))
x
M ( x, y )
y
3

4.

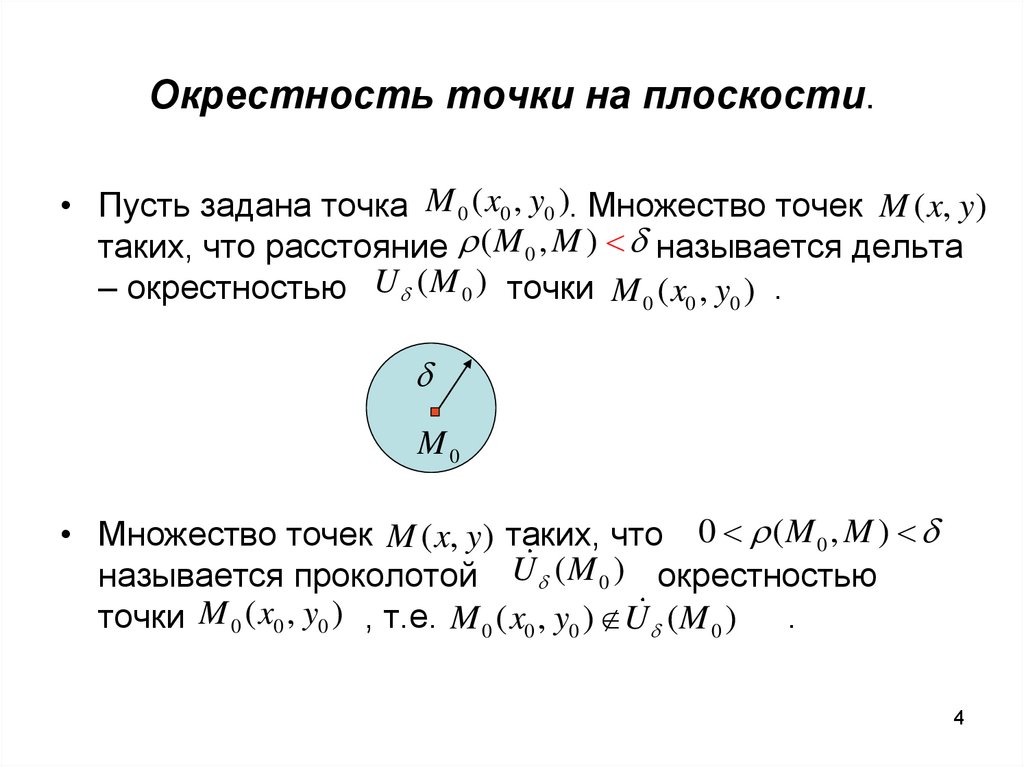
Окрестность точки на плоскости.
• Пусть задана точка M 0 ( x0 , y0 ). Множество точек M ( x, y )
таких, что расстояние ( M 0 , M ) называется дельта
– окрестностью U ( M 0 ) точки M 0 ( x0 , y0 ) .
M0
• Множество точек M ( x, y ) таких, что 0 ( M 0 , M )
называется проколотой U ( M 0 ) окрестностью
точки M 0 ( x0 , y0 ) , т.е. M 0 ( x0 , y0 ) U ( M 0 ) .
4

5.

Предел функции
• Пусть функция z f ( x, y ) определена в некоторой
окрестности точки M 0 ( x0 , y0 ) кроме, быть может
самой точки. Числа A
называется пределом
функции z f ( x, y ) при x x0 , y y0 ,
A lim f ( x, y )
x x0
y y0
• если для любого числа 0
найдётся
проколотая окрестность U ( M 0 )
такая, что
f ( x, y ) A
• для всех точек M ( x, y ) U ( M 0 ) .
5

6.

Свойства пределов
• Свойства пределов, доказанные для функций одной
переменной, а также арифметические свойства
пределов аналогично доказываются и для функций
двух переменных.
6

7.

Непрерывность функции
• Если предел функции при x x0 , y y0 совпадает
со значением функции z0 f ( x0 , y0 )
z0 lim f ( x, y )
x x0
y y0
• то функция z f ( x, y ) называется непрерывной в
точке M 0 ( x0 , y0 ).
• Замечание. Из непрерывности функции по каждой
переменной не следует непрерывность как функции
двух переменных.
xy
z 2
x y2
7

8.

Частные производные
• Приращением функции z f ( x, y ) по переменной x
называется величина
x z f ( x x, y ) f ( x, y )
• Частной производной по x в точке ( x, y )
называется предел
x z
z
z x
lim
.
x x 0 x
• Аналогично определяется производная по
yz
z
z y
lim
.
y
0
y
y
y
8

9.

Вычисление частных производных
• Частная производная по x является обычной
производной от функции z f ( x, y ) как функции
только одной переменной x , рассматривая
переменную
y как константу.
• Аналогично при нахождении производной по y
переменная x рассматривается как константа.
• Пример.
x
3
z x cos xy
y
9

10.

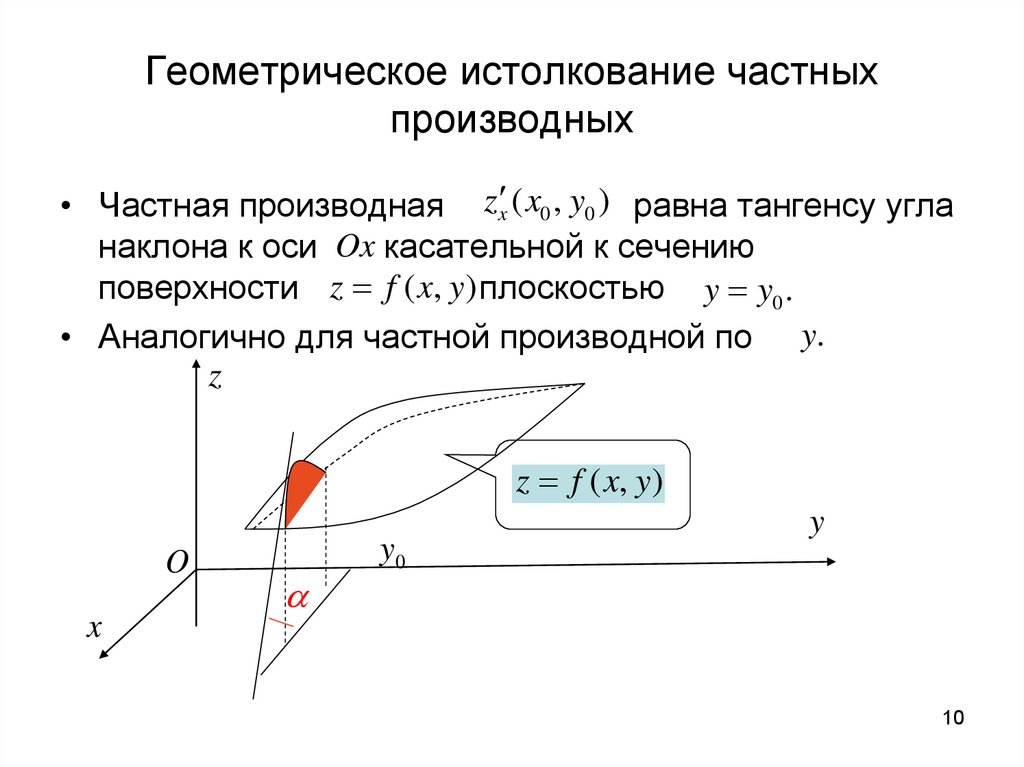
Геометрическое истолкование частных
производных
• Частная производная z x ( x0 , y0 ) равна тангенсу угла
наклона к оси Ox касательной к сечению
поверхности z f ( x, y ) плоскостью y y0 .
• Аналогично для частной производной по y.
z
z f ( x, y )
O
x
y0
y
10

11.

Производные высших порядков
• Производная второго порядка по переменной x
определяется формулой
2 z z
.
2
x
x x
• Смешанная производная второго порядка 2 z
z
.
x y x y
• Аналогично определяются производные
2 z
,
2
y
2 z
.
y x
11

12.

Теорема о смешанных производных
• Если функция z f ( x, y ) определена в окрестности
точки M 0 ( x0 , y0 ). вместе со своими производными
z
,
x
z
,
y
2 z
,
x y
2 z
y x
• и смешанные производные непрерывны в точке M 0 ,
то
2 z
2 z
(M 0 )
( M 0 ).
x y
y x
12

13.

Функции трёх и более переменных.
• Если каждой упорядоченной тройке ( x, y, z ) D
по некоторому правилу ставится в соответствие
число u
, то говорят, что на множестве D
задана функция трёх переменных u f ( x, y, z ).
n
• Аналогично определяется функция
переменных
u f ( x1 , x2 , , xn ).
• Также, с помощью окрестности точки можно
определить предел, непрерывность функций трёх и
более переменных , а также частные производные.
13

14.

Теорема о приращении функции
• Рассмотрим для простоты случай двух переменных.
Случай n, n 2 переменных рассматривается
аналогично.
• Приращением функции u f ( x, y ) в точке ( x, y, )
называется разность
u f ( x x, y y ) f ( x, y ).
• Если функция u f ( x, y )
имеет непрерывные
частные производные в точке ( x, y ) , то
f
f
u x y o( ), 0,
x
y
x 2 y 2 .
14

15.

Дифференцируемость функции
• Опр/ Функция u=f(x,y), полное приращение Δu
которой в данной точке ( x, y ) м.б.представлено в
виде суммы двух слагаемых: линейного выражения
относительно x, y и величины БМ высшего
порядка относительно Δρ, называется
дифференцируемой в данной точке, а линейная
часть приращения наз-ся полным дифференциалом
и обозначается через dz или df.
• Теорема 2. Для того чтобы функция была
дифференцируема в точке, необходимо чтобы она
имела в этой точке частные производные, и
достаточно, чтобы частные производные были
непрерывны в этой точке.
15

16.

Дифференциал
• Если функция дифференцируем в точке
главная часть приращения функции
f
f
du
x y
x
y
(х,у) , то
• называется дифференциалом. Дифференциал
записывается также в виде
f
f
du
dx dy.
x
y
• В случае трёх переменных
f
f
f
du
dx dy dz.
x
y
z
16

17.

Производная сложной функции
• Теорема. Если функция u f ( x, y, z )
дифференцируема в точке ( x, y, z ) , а функции
x (t ), y (t ), z (t )
• имеют производную в точке t
, то производная
сложной функции u f ( (t ), (t ), (t )) вычисляется
по формуле
du u dx u dy u dz
.
dt x dt y dt z dt
17

18.

Производная сложной функции
• Если функции x x ( , ), y y( , ), z z ( , )
зависят от двух переменных, то частные
производные сложной функции u f ( x, y, z )
вычисляются по формулам
u u x u y u z
,
x y z
u u x u y u z
.
x y z
18

19.

Существование неявной функции
• Рассмотрим условия существования неявной
функции, которая задаётся уравнением F ( x, y ) 0
Пусть функция F ( x, y )
в некоторой
окрестности точки M 0 ( x0 , y0 ) и частная
производная Fy непрерывны в точке M 0 . Тогда,
если F ( x0 , y0 ) 0 и Fy ( x0 , y0 ) 0 , то существует
прямоугольная окрестность x x0 , y y0
такая, что в этом прямоугольнике существует
y f ( x ), y0 f ( x0 ) ,
единственная кривая
удовлетворяющая уравнению F ( x, f ( x )) 0, x U ( x0 ),
• и y f ( x ) дифференцируема при x U ( x0 ) .
19

20.

Производные неявной функции
• В условиях существования неявной функции
справедлива формула ее производной y f ( x )
Fx ( x, y )
y
.
Fy ( x, y )
• Аналогично для частных производных неявной
функции двух переменной z z ( x, y ) , задаваемой
уравнением
F ( x, y, z ) 0 , справедливы формулы
Fx ( x , y )
Fx ( x , y )
zx
, zy
.
Fz ( x , y )
Fz ( x , y )
20

21.

Производная по направлению
• Рассмотрим функцию u f ( x, y, z ) , определённую
в окрестности точки M 0 ( x0 , y0 , z0 ) . Пусть l
ось, проходящая через точку M 0
,
а n (cos , cos , cos )
единичный вектор в
направлении оси.
x x0 t cos
l
M
M : y y0 t cos
M0
n
z z t cos
0
u
• Производной по направлению
называется
l
производная ut , где
u f ( x x0 t cos , y0 t cos , z z0 t cos ).
21

22.

Вычисление производной по направлению
• Если функция u f ( x, y, z ) дифференцируема в
точке M 0 ( x0 , y0 , z0 )
, то справедлива формула в
этой точке
u u
u
u
cos
cos
cos
l x
y
z
22

23.

Градиент. Формула
Тейлора

24.

Градиент
• Градиентом функции
u f ( x, y, z )
M ( x , y, z ) называется вектор
точке
в
u
u
u
grad u
i
j
k
x
y
z
• где частные производные вычисляются в точке M .
• Справедлива формула
u
grad u n,
l
• где
n - единичный вектор в направлении
l
.
24

25.

Свойства градиента
• Справедливо неравенство
u
grad u
l
• Свойства градиента.
• 1. Длина градиента равна максимальной величине
производной по направлению.
• 2. Градиент направлен в ту же сторону, что и ось
вдоль которой берётся производная по направлению.
• 3. Если градиент равен нулю, то u 0 для любого
l
направления l .
25

26.

Касательная плоскость.
• Если функция z f ( x , y ) дифференцируема в
точке M 0 ( x0 , y0 )
• Плоскость, заданная уравнением
f
f
z z0
( M 0 )( x x0 ) ( M 0 )( y y0 )
x
y
• называется касательной плоскостью к поверхности
z f ( x, y ) в точке ( x0 , y0 , z0 ), z0 f ( x0 , y0 ) , а
соответствующее значение z аппликатой
касательной плоскости:
f
f
z z0 ( M 0 )( x x0 ) ( M 0 )( y y0 )
x
y
26

27.

Геометрическое истолкование
дифференциала
x x x 0 , y y y 0 , z z z 0 .
• Обозначим
• Тогда уравнение касательной плоскости примет вид
f
f
z ( M 0 ) x ( M 0 ) y.
x
y
• Или z dz, где величина z
называется
приращением аппликаты касательной плоскости.
27

28.

Свойство касательной плоскости.
• Если функция z f ( x , y ) дифференцируема в
точке M 0 ( x0 , y0 ) , то справедлива формула
f
f
z ( M 0 ) x ( M 0 ) y o( ), 0,
x
y
• Тогда
f
f
f ( x, y ) z0 ( M 0 )( x x0 ) ( M 0 )( y y0 ) o( ), 0,
x
y
• Отсюда , если Z- аппликата касательной
плоскости в точке M ( x , y ), то расстояние
f ( x, y ) Z o( ), 0
28

29.

Дифференциалы высшего порядка
Определим дифференциал второго порядка
функции u f ( x1 , x2 , , xn )
формулой
d u d (du).
2
• Дифференциал
n
- го порядка по индукции
d n u d (d n 1u).
• В частности для функции
u f ( x1 , x2 )
u
u
u
2
d u 2 (dx ) 2
dxdy 2 (dy ) 2 .
x
x y
y
2
2
2
2
29

30.

Формула Тейлора
• Пусть функция z f ( x , y ) имеет непрерывные
производные до порядка n 1
включительно в
некоторой окрестности точки M 0 ( x0 , y0 )
. Если
точка M ( x , y ) из этой окрестности, то
справедлива формула Тейлора
df ( M ) d 2 f ( M )
0
0
f (M ) f (M )
0
1!
2!
• где
P
df
( M ) df (n 1) ( P )
0
,
n!
(n 1)!
( n)
некоторая точка из окрестности точки
M0.
30

31.

Экстремум функций
многих переменных

32.

Определения
• Случай двух переменных. Пусть функция z f ( x , y )
определена в окрестности точки M 0 ( x0 , y0 ). Если
для всех точек M ( x , y ) из некоторой
окрестности точки M 0 ( x0 , y0 )
выполняется
неравенство
f ( x, y ) f ( x0 , y0 ), ( f ( x, y ) f ( x0 , y0 ))
то точка M 0 ( x0 , y0 ) называется точкой минимума
(максимума) функции z f ( x , y ) .
• Точки минимума и максимума называются точками
экстремума.
32

33.

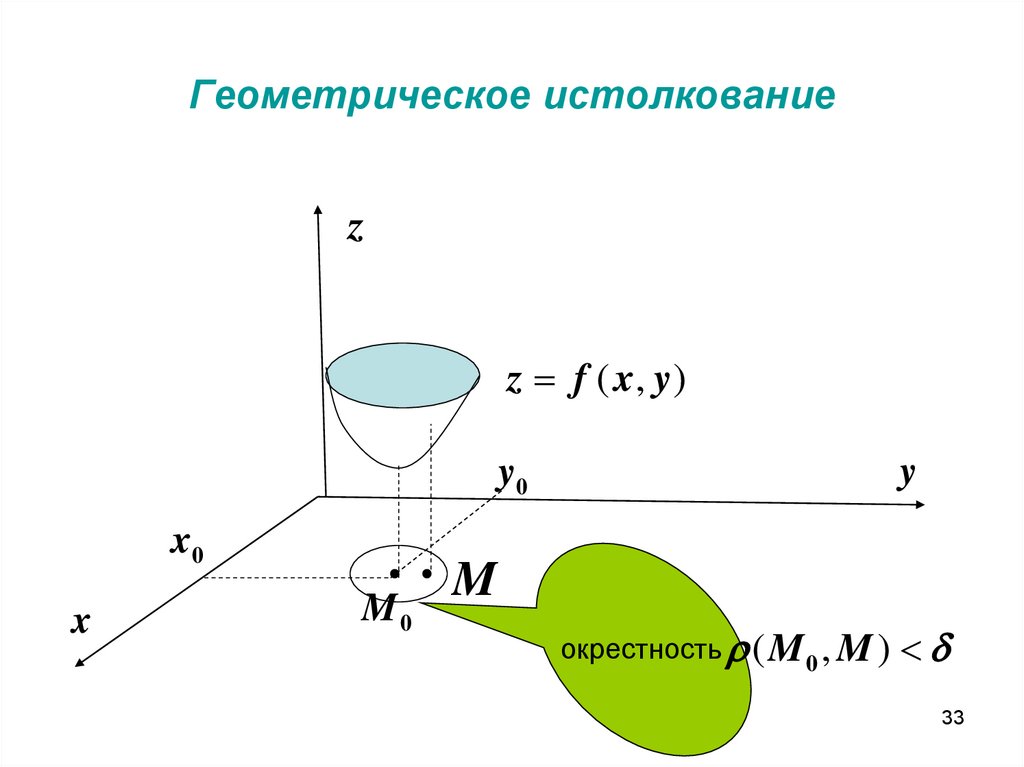
Геометрическое истолкование
z
z f ( x, y )
y
y0
x0
x
M0
M
окрестность ( M 0 , M )
33

34.

Необходимое условие экстремума
• Теорема. Пусть функция z f ( x , y ) имеет
экстремум в точке имеет экстремум в точке
M.0 ( x0 , y0 ) Если существуют частные производные
первого порядка в точке
,
M 0 ( x 0 , y0 )
то они обращаются в нуль в этой точке
df
df
(M0 )
( M 0 ) 0.
dx
dy
• Следствие. Если функция z f ( x , y ) имеет
экстремум в точке M 0 ( x0 , y0 ) и дифференцируема
в этой точке, то df ( M ) 0 и grad f ( M ) 0
0
0
34

35.

Замечание
• Условия равенства нулю производных являются
необходимыми условиями, но не являются
достаточными условиями.
• Пример.
z x2 y2
35

36.

Достаточные условия экстремума
• Теорема 1. Пусть функция z f ( x , y ) имеет
непрерывные производные до второго порядка
включительно в окрестности точки M 0 ( x0 , y0 ) и
df ( M 0 ) 0.
2
• Тогда, если d f ( M 0 ) 0 для любых
dx , dy
одновременно не равных нулю, то функция z f ( M )
имеет в точке M ( x , y ) минимум, если
0
0
0
df
(
M
)
0
,
то – максимум. Если же второй
0
дифференциал
df ( M 0 ) может принимать как
положительные, так и отрицательные значения, то
функция z f ( M )
не имеет экстремума в M 0 .
36

37.

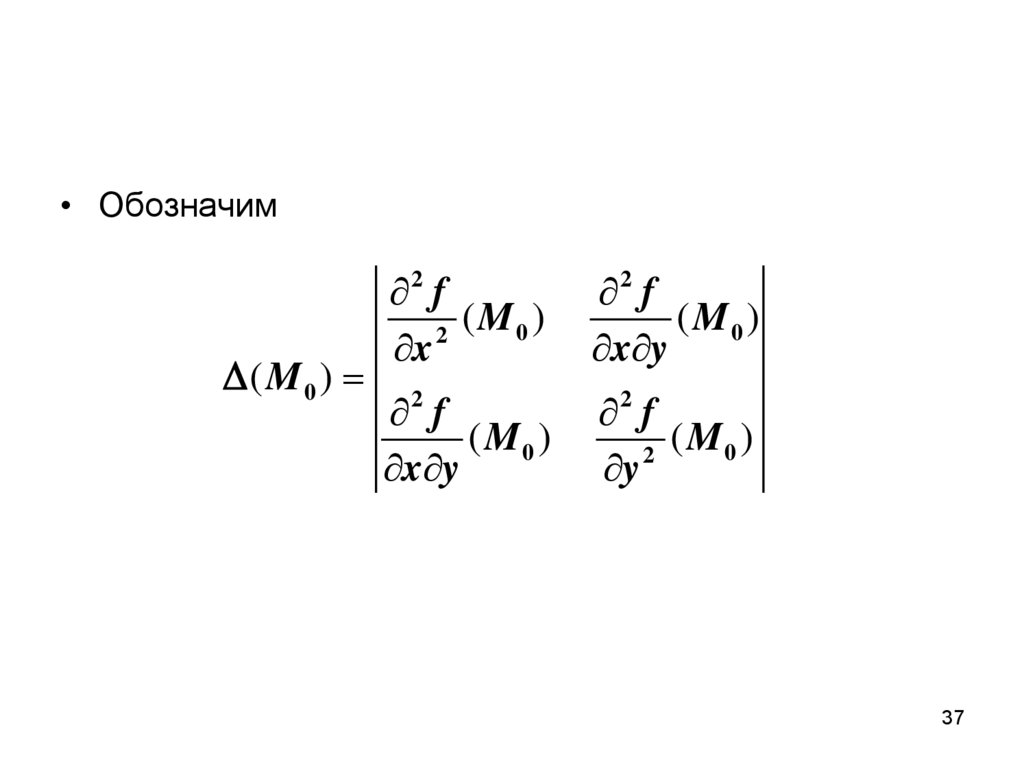
• Обозначим
(M0 )
2 f
(M0 )
2
x
2 f
(M0 )
x y
2 f
(M0 )
x y
2 f
(M0 )
2
y
37

38.

Достаточные условия экстремума
• Теорема 2. Пусть выполняются условия теоремы 1
на гладкость функции z f ( M ) и df ( M 0 ) 0.
Если ( M 0 ) 0 , то точка M 0 . является точкой
экстремума причём,
если
2
f
(M0 ) 0 2
2
f
x
то точкой минимума , если x 2 ( M 0 ) 0- точкой
максимума. Если ( M ) 0,
0
то экстремума нет. Если ( M 0 ) 0
сказать нельзя".
, то"ничего
38

39.

Пример
• Исследовать на экстремум
z x 3 y 3 3 xy 1
39

40.

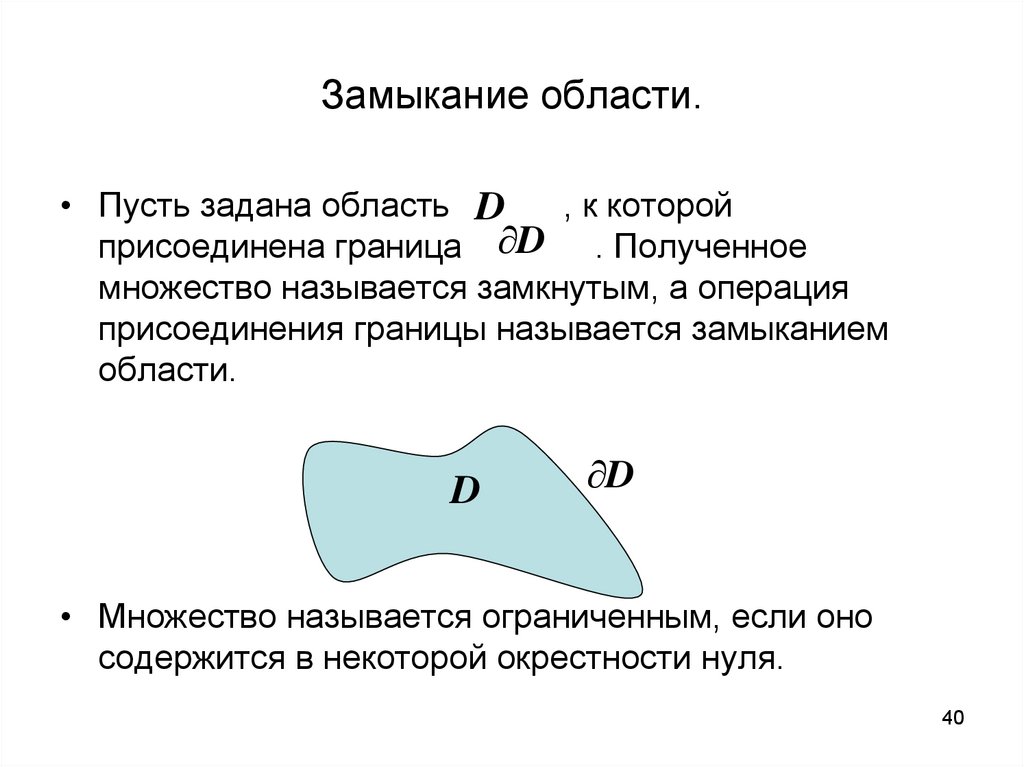
Замыкание области.
• Пусть задана область D
, к которой
присоединена граница D . Полученное
множество называется замкнутым, а операция
присоединения границы называется замыканием
области.
D
D
• Множество называется ограниченным, если оно
содержится в некоторой окрестности нуля.
40

41.

Наибольшее и наименьшее значения
функции
• Теорема. Если функция z f ( M ) непрерывна на
замкнутом ограниченном множестве G
, то
существуют точки, принадлежащие множеству G ,
в которых функция принимает наибольшее и
наименьшее значения, т.е. существую точки
A G, B G
• такие, что
f ( A) max f ( M ),
M G
f ( B ) min f ( M ).
M G
41

42.

Нахождение наибольшего и наименьшего
значений функции
• Пусть функция z f ( x , y )
задана на
замкнутом множестве G
. Чтобы найти
наибольшее и наименьшее значения функции надо
найти значения функции в стационарных точках,
лежащих внутри G , и сравнить со значениями
функции на границе.
• Пример. Найти наибольшее и наименьшее значения
функции z x 2 x 2 y 1
на множестве
x y 1, x 0, y 0.
42