Similar presentations:
Электромагнитные соотношения
1. 1.7. Основные электромагнитные соотношения
ЭДС якоря. ЭДС якоря определяетсяE k Ф
p N
где k
- конструктивный коэффициент
2 a
машины.
Таким образом ЭДС пропорциональна
основному магнитному потоку и частоте
вращения и не зависит от формы кривой
распределения индукции в воздушном зазоре.
2.
Электромагнитный момент.Электромагнитный момент определяется: М =
kФI.
Таким образом, электромагнитный
момент пропорционален основному
магнитному потоку и току и также не
зависит от формы кривой распределения
индукции в воздушном зазоре.
3. 1.8. Уравнения электромеханического преобразования энергии
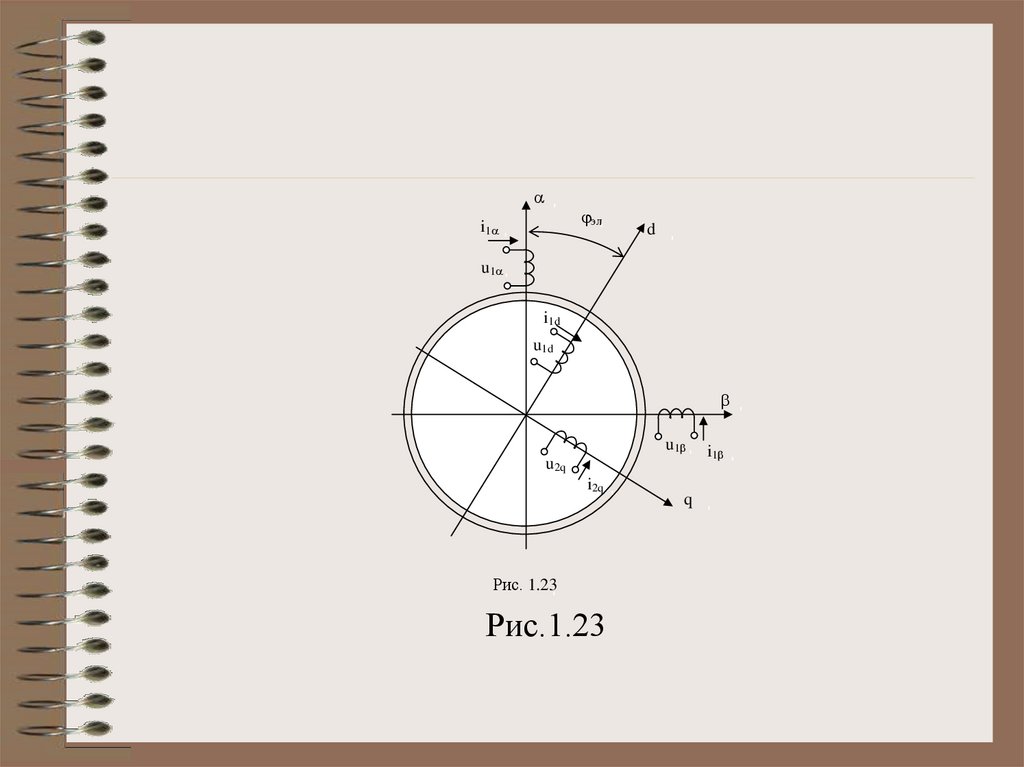
Рассмотрим двухфазную двухполюсную ЭМ,имеющую 2 ортогональные системы
обмоток. Принята следующая индексация: 1
– статорные параметры, 2 – роторные
параметры; ,
- система координат
жестко связанная со статором; d, q - система
координат, жестко связанная с ротором (рис.
1.23).
4.
i1эл
d
u1
i1d
u1d
u1
u2q
i2q
Рис. 1.23
Рис.1.23
q
i1
5.
Динамика обобщенной машиныописывается 4 уравнениями
электрического равновесия в цепях ее
обмоток и уравнением
электромеханического преобразования
энергии, которое выражает
электромагнитный момент ЭМ как
функцию электрических и
механических координат системы.
6.
на основании второго закона Кирхгофа изакона Фарадея можно записать следующую
систему координат для каждой из четырех
пар зажимов
d 1
U 1 R 1 i 1
U 1 R 1 i 1
U 2d
U 2q
dt
d 1
dt
d 2 d
R 2 i 2d
dt
d 2 q
R 2q i 2q
dt
(1.5)
7.
где d dt E - закон Фарадея (наведеннаяЭДС прямо пропорциональна изменению
потосцепления)
Уравнения (1.5) записаны для реальных
напряжений, токов и параметров
обобщенной машины , т.е. для обмоток
статора в осях , ,0 , неподвижных
относительно статора, а для ротора – в осях
координат d,q,0 , неподвижных относительно
ротора.
8.
Уравнения системы (1.5) однотипны и их можнозаписать в обобщенной форме:
d i
Ui R i i i
dt
Потокосцепление каждой обмотки в общем
виде определяется результирующим
действием токов всех обмоток ЭМ (система
(1.6):
9.
1 L1 ,1 i1 L1 ,1 i1 L1 ,2d i 2d L1 ,2q i 2q1 L1 ,1 i1 L1 ,1 i1 L1 ,2d i 2d L1 ,2q i 2q
2d L 2d,1 i1 L 2d,1 i1 L 2d,2d i 2d L 2d,2q i 2q
2q L 2q,1 i1 L 2q,1 i1 L 2q,2d i 2d L 2q,2q i 2q
(1.6)
10.
В системе уравнений (1.6) перваячасть индекса у индуктивности
указывает в какой обмотке наводится
ЭДС, а вторая – током какой обмотки
она наводится. Например L2d,2d –
собственная индуктивность фазы d
ротора, а L2d,2q – взаимная
индуктивность между фазами d и q
ротора.
11.
В более компактной форме уравнения (1.6) могутбыть записаны:
i
j 2 q
L
j 1
i,j
ij
(1.7)
При работе ЭМ взаимные индуктивности обмоток
статора и ротора изменяются, поэтому собственные
и взаимные индуктивности обмоток, в общем
случае, являются функцией электрического угла
поворота ротора
L i , j f эл
12.
При симметричной неявнополюсной ЭМсобственные индуктивности обмоток статора и
ротора не зависят от положения ротора:
L1 ,1 L1 ,1 L1 const
L 2d , 2d L 2q , 2q L 2 const
а взаимные индуктивности между обмотками статора
и ротора равны нулю:
L1 ,1 L1 ,1 L 2d , 2q L 2q , 2d 0
т.к. математические оси этих обмоток сдвинуты в
пространстве относительно друг друга на 900.
13.
Взаимные индуктивности обмотокстатора и ротора проходят полный цикл
изменения при повороте ротора на
электрический угол 3600, поэтому с
учетом принятых на рис. 1.23
направлений токов и знака угла
поворота ротора можно записать:
14.
L1 , 2d L 2d ,1 L1, 2 cos элL1 , 2q L 2q ,1 L1, 2 cos эл 900 L1, 2 sin эл
L1 , 2q L 2q ,1 L1, 2 cos эл
L1 , 2d L 2d ,1 L1, 2 cos 900 эл L1, 2 sin эл
(1.8)
15.
Таким образом для неявнополюснойобобщенной машины уравнения
электрического равновесия с учетом (1.6) –
(1.8):
U1 R 1 i 1 pL 1 i 1 pL 1, 2 (cos эл ) i 2d pL 1, 2 sin эл i 2q
U1 R 1 i 1 pL 1 i 1 pL 1, 2 sin эл i 2d pL 1, 2 cos эл i 2q
U 2d R 2 i 2d pL 2 i 2d pL 1, 2 cos эл i 1 pL 1, 2 sin эл i 1
U 2q R 2 i 2q pL 2 i 2q pL 1, 2 sin эл i 1 pL 1, 2 cos эл i 1
(1.9)
16.
В более компактном виде уравнения (1.9):d
U i R i i1
dt
j 2 q
L
j 1
i,j
ij
(1.10)
Обобщенная машина образует единую
электромеханическую связь: механическое движение
оказывает влияет на электрическую систему, а
электрическое движение – на механическую систему.
Влияние механического движения на электрическую
систему автоматически включено в электрические
уравнения движения в силу закона Фарадея в
U p т.к. f
соответствии с которым
17.
Таким образом выражениеp
содержит напряжения, обусловленные
механическим движением.
Влияние электрического движения на
механическое выражается в уравнении
электромагнитного момента.
Выражение электромагнитного момента
можно получить на основе принципа
возможных перемещений и закона
сохранения энергии.
18.
Если валу ЭД сообщено произвольное перемещениеза время dt , то на основе закона сохранения
энергии:
d
4
2
M d i j j dWмех dWm d dt
j 1
Или сообщенная механическая энергия + сообщенная
электрическая энергия = изменения в сообщенной
механической энергии + изменения в сообщенной
электрической энергии + потери
19.
После соответствующих преобразованийпоследнего выражения уравнение
электромагнитного момента:
1 Wm 1
1
M
ii i
2
2 i 1
2 i 1
2q
1 2q
i
M ii
2 i 1
2q
ii
i
(1.11)
20.
Преобразовав выражение (1.11) с помощьювыражения (1.7)
L i , j
1
M 2q i i
ij
2
i 1
i 1
2q
(1.12)
21.
Таким образом уравнения (1.11) и (1.12)полностью характеризуют обобщенный
вращающийся электромеханический
преобразователь энергии относительно его
четырех пар электрических зажимов и пары
механических зажимов:
d 2q
Ui R i i i Li,j i j
dt i 1
(1.13)
L i , j
1 2q
M ii
ij
2 i 1
22.
Эти уравнения, записанные черездействительные переменные
двухфазной модели, представляют
собой развернутое математическое
описание динамического процесса
электромеханического преобразования
энергии, которое может быть
конкретизировано для различных ЭД:
АД, СМ, ДПТ, МДП и т.д.
23.
Уравнения (1.13) образуют систему из 5уравнений, устанавливающую
взаимосвязь между процессами в
механической и электрической частями
ЭМС. Проявление такой взаимосвязи
называется в теории ЭП –
электромеханической связью.
24.
Выполнив дифференцирование первогоуравнения системы (1.13):
2q
Ui R i ii Li,j
di i , j
2q
ij
dL i , j
dt i 1
dt
d
d
из выражения
dt
dt
di i , j
dL i , j
Ui R i ii Li,j
ij
dt
d
i 1
25.
Рассмотрим все слагаемые последнеговыражения.
Riii - представляет собой падение
напряжение на активном сопротивлении
данной
цепи,
2q
di j
Li,j
результирующая ЭДС
dt
i 1
самоиндукции и взаимной индукции,
вызванные изменением токов в обмотках,
26.
2qL i , j
i j ei
- отражает
взаимодействие механической и
электрической частей ЭМ, т.к. представляет
собой результирующую ЭДС ei , наведенную
в обмотке в результате механического
движения ротора ЭМ.
j 1
27. 1.9. Параметры ЭМ
Параметры ЭМ – это коэффициенты переднезависимыми переменными в уравнениях,
описывающих электромеханическое
преобразование энергии.
Обычно независимые переменные – это токи.
Уравнения могут быть как
дифференциальные, так и комплексными и
алгебраическими.
(Самостоятельно)
28. 1.10. Система относительных единиц
Система о.е. широко используется как втеории ЭМ, так и в теории ЭП. В этой системе
U, I, P и параметры выражаются в
относительных единицах, т.е. в долях
базисных значений этих величин. В качестве
базисных величин принимаются
номинальные значения.
Относительные величины обозначаются
звездочкой.
(Самостоятельно).












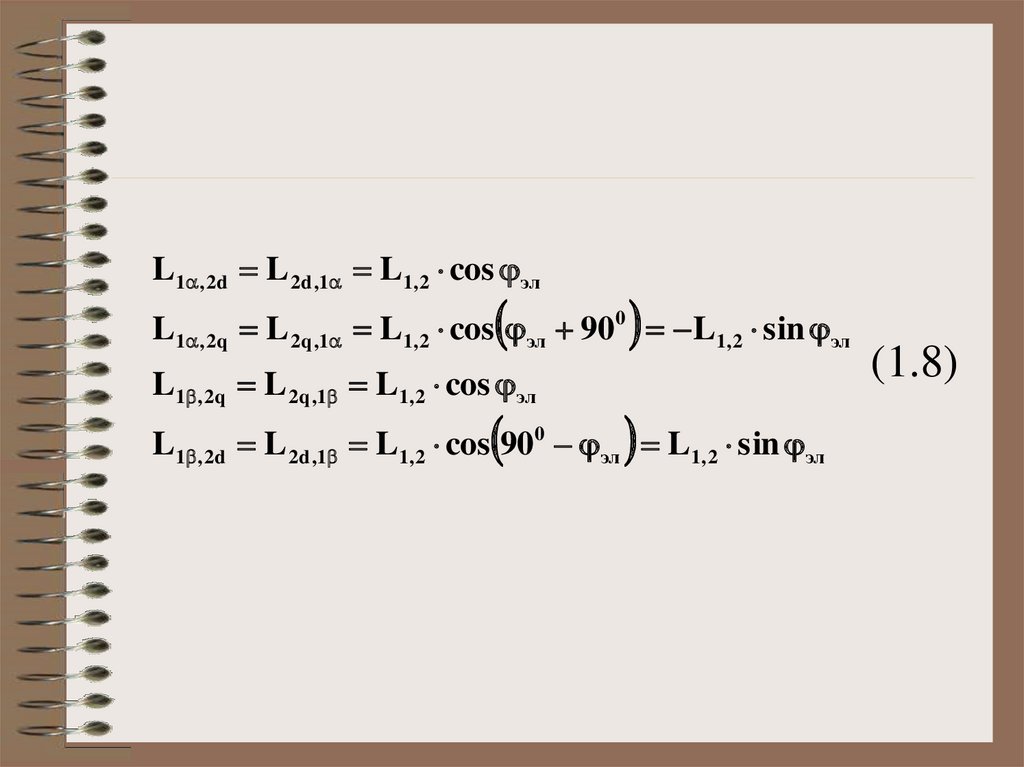














 electronics
electronics








