Правила нахождения первообразных

1.

Тема урока:

2.

Таблицу первообразных можно
составить , используя таблицу
производных.
(cosx)' = - sinx
( - sinx)' = - cosx
F(x)= - cosx + C

3.

Таблица первообразных:
f(x)
F(x)
1
к
кх С
2
р
х р 1
С
р 1
3
х
р 1
р 0
р 1
(к х b)
4
1
х
5
1
кх в
р
х 0
к 0
(к х b) р 1
С
к(р 1)
lnх С
1
ln кх в С
к

4.

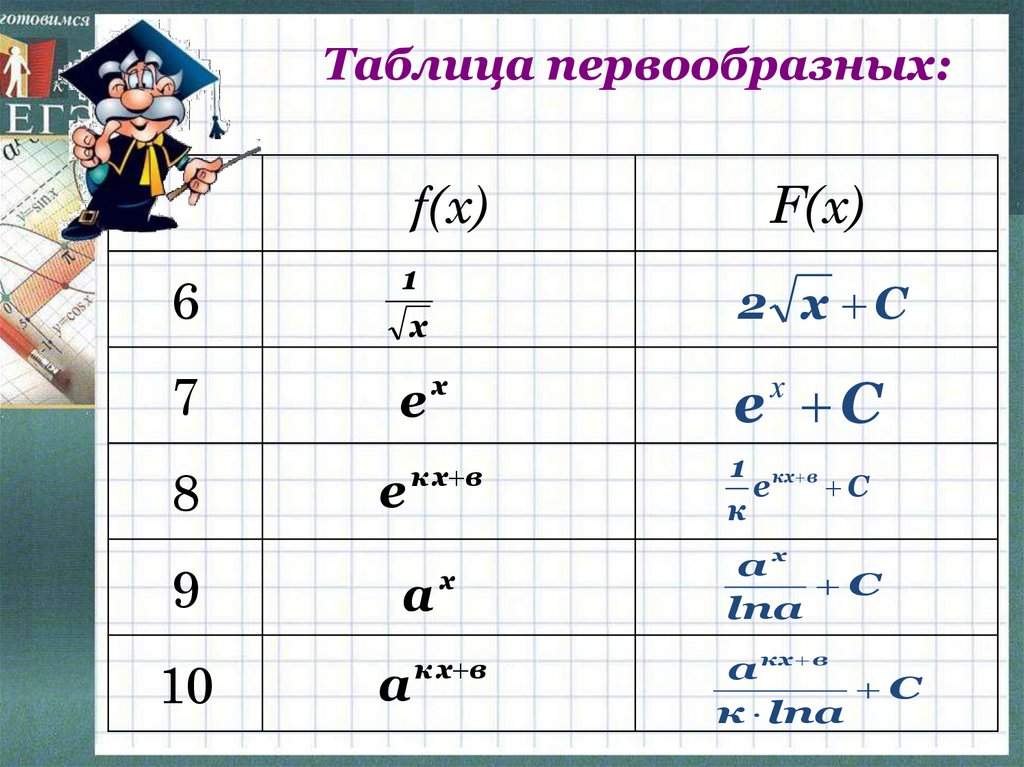
Таблица первообразных:
f(x)
6
7
8
9
10
1
х
е
е
F(x)
2 х С
х
е С
х
к х в
1 кх в
е
С
к
х
ах
С
lna
а
а
к х в
а кх в
С
к lna

5.

Таблица первообразных:
11
12
13
f(x)
F(x)
sinx
- cosх С
sin кx в
к 0
cosx
14
cos кx в
15
1
cos 2 х
16
1
sin 2 х
-
1
cos кх в С
к
sinх С
к 0
1
sin кх в С
к
tgх С
- ctgх С

6.

Для нахождения первообразных нам понадобятся
кроме таблицы правила нахождения первообразных.
Правила интегрирования
1) Если F(x)– первообразная для функции f(x), а
G(x)– первообразная для функции g(x), то
F(x)+G(x)– первообразная
для функции
f(x)+g(x).
Первообразная
суммы
равна
сумме первообразных
2) Если F(x)– первообразная для функции f(x),
а а –константа, то аF(x)– первообразная
для функции аf(x).Постоянный множитель можно
выносить за знак первообразной
3) Если F(x) – первообразная для функции f(x), а k и b1
константы, причем k≠0, то F ( kx b )- первообразная для
k
функции f ( kx b ).
23.03.2021
7

7.

Задача. Дана функция f(x). Найдите ее
первообразную, воспользовавшись таблицей
первообразных и правилами нахождения
первообразной и выполните проверку,
1)
2
f(x) 2
x
В таблице такой функции нет.
Коэффициент
Преобразуем
f(x):
Табличная
F( x ) ?
2
1
f( x) 2 2 2
x
x
1
F( x ) 2 2
x
x
Проверка:
функция
Используем таблицу
и второе правило.
1 2
2
1
F ( x ) 2 2 2 2 f ( x )
x x
x
x
F ( x ) первообразная
для
f(x)

8.

Задача. Дана функция f(x). Найдите ее
первообразную, воспользовавшись таблицей
первообразных и правилами нахождения
первообразной
2)
f(x) x x
F( x ) ?
2
16
Табличная
функция
Табличная
функция
Используем таблицу
и первое правило.
x 2 1
x 16 1
x 3 x 17
F( x )
2 1 16 1
3 17
x
1 3 1
x
Проверка: F ( x )
( x )
( x 17 )
3
17
17
3
1
1
2
16
2
3x
17 x 16 x x f ( x )
3
17
3
17
F ( x ) первообразная
для
f(x)

9.

Задача . Дана функция f(x). Найдите ее
первообразную, воспользовавшись таблицей
первообразных и правилами нахождения
первообразной
Коэффициент
Коэффициент
3)
f ( x ) 3 sin x 2 cos x Используем таблицу,
первое и второе правило.
F( x ) ?
Табличная
Табличная
F ( x ) 3( cos x ) 2 sin x
функция
функция
3 cos x 2 sin x
Проверка:
F ( x ) ( 3 cos x 2 sin x ) 3 sin x 2 cos x f ( x )
F ( x ) первообразная
для
f(x)

10.

Задача . Дана функция f(x). Найдите ее
первообразную, воспользовавшись таблицей
первообразных и правилами нахождения
первообразной
4)
f ( x ) sin( 3 x ) Синус – табличная функция.
Табличная
Аргумент – линейная функция (k=3).
F
(
x
)
?
функция
Используем таблицу и третье правило.
1
1
F ( x ) ( cos( 3 x )) cos( 3 x )
3
3
Проверка:
1
1
F ( x ) cos( 3 x ) cos( 3 x )
3
3
1
1
( sin( 3 x ))( 3 x ) sin( 3 x ) 3 sin( 3 x )
3
3
f ( x ) F ( x ) первообразная
для
f(x)

11.

№ 988-991(неч.).

12.

№ 988-991
(чет.).