Similar presentations:
Первообразная. Правила нахождения первообразных
1.
ПервообразнаяПравила нахождения
первообразных
2.
Функция F(x)называетсяпервообразной для функции f(x)на
некотором промежутке, если для
всех x из этого промежутка
F ( x) f ( x)
3.
5Показать, что функция
x
F ( x) 1
5
является первообразной для функции
4
f ( x) x
Решение:
5
4
x
5x
4
F ( x) 1
x f ( x)
5
5
4.
Показать, что функция F ( x) 1 sin2x
является первообразной для функции
f ( x) 2 cos 2 x
Решение:
F ( x) 1 sin 2 x 2 cos 2 x f ( x)
5.
Если F(x)– первообразная дляфункции f(x) на некотором
промежутке, то функция F(x)+C
также является первообразной
функции f(x) на этом промежутке,
где C –произвольная постоянная.
6.
f ( x) 1F ( x) х C
7.
f ( x) х1 2
F ( x) х C
2
8.
f ( x) x , p 0p
p 1
x
F ( x)
C
p 1
9.
1f ( x) , x 0
x
F ( x) ln x C
10.
f ( x) ex
F ( x) e C
x
11.
f ( x) sin xF ( x) cos x C
12.
f ( x) cos xF ( x) sin x C
13.
Правила нахожденияпервообразных
14.
Если F(x)– первообразная для функции f(x),а G(x)– первообразная для функции g(x), то
F(x)+G(x)– первообразная для функции
f(x)+g(x)
Первообразная суммы равна
сумме первообразных
15.
Если F(x)– первообразная для функции f(x),а а –константа, то аF(x)– первообразная
для функции аf(x)
Постоянный множитель
можно выносить за знак
первообразной
16.
Если F(x) – первообразная для функцииf(x), а k и b- константы, причем k 0
1
то
F (kx b) - первообразная для
функции
k
f (kx b)
17.
f ( x) sin хF ( x)
1
cos х C
18.
f ( x) cos хF ( x)
1
sin х C
19.
Найти первообразные для функцииf ( x) 5 x e
3
2 x 7
4 cos x
Решение:
4
x 1 2 x 7
F ( x) 5 e
4 sin x C
4 2
20.
Найти первообразные для функции:1) f ( x ) 3 x 5
4
2) f x 6e
3 x 1
x
1
3) f x 5 sin 2 x
x
21.
Найти первообразные для функции:Ответы:
3 5
1) F ( x) x 5 x C
5
2
x
3 x 1
2) f x 2e C
2
5
3) f x cos 2 x ln x C
2








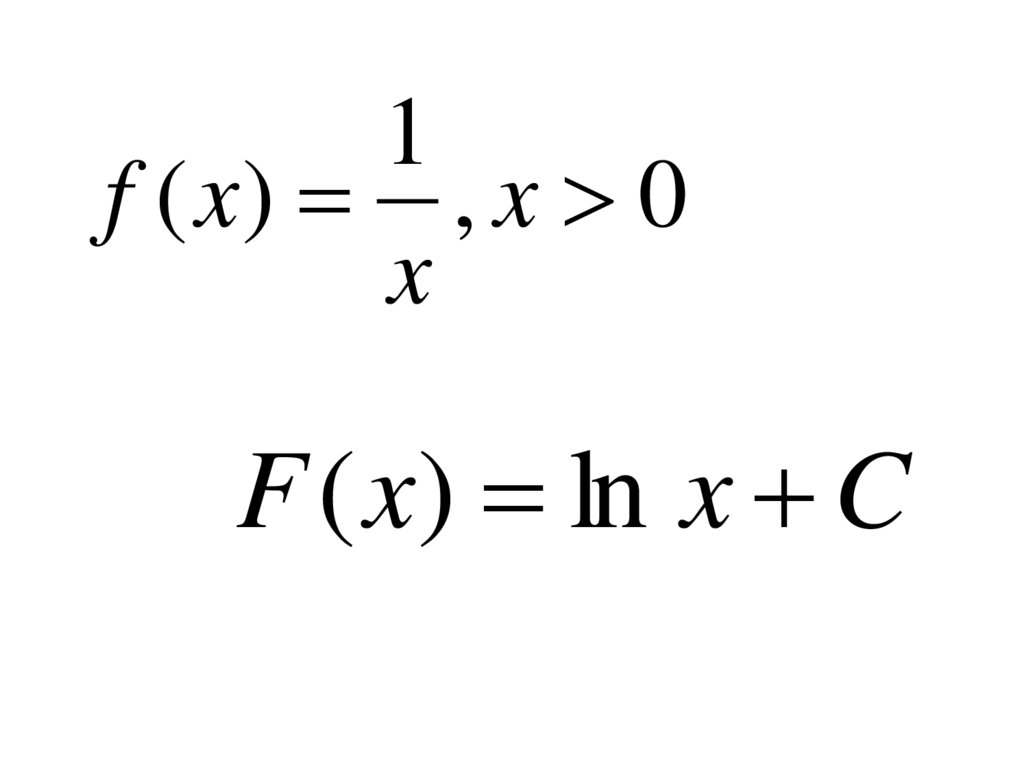
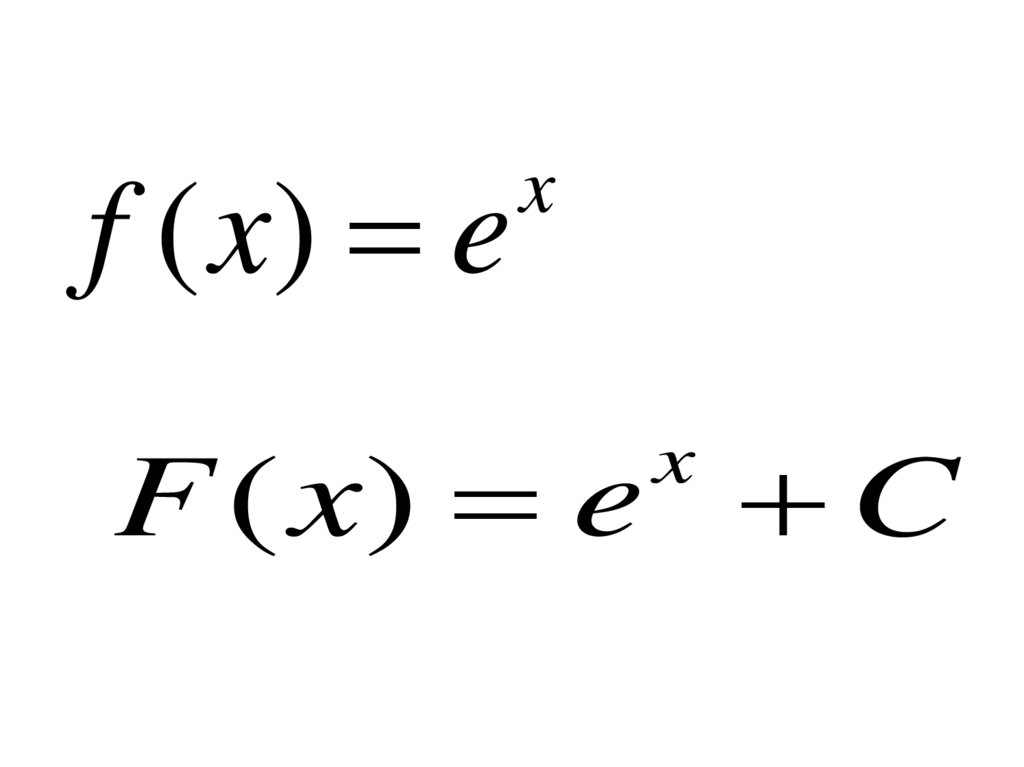






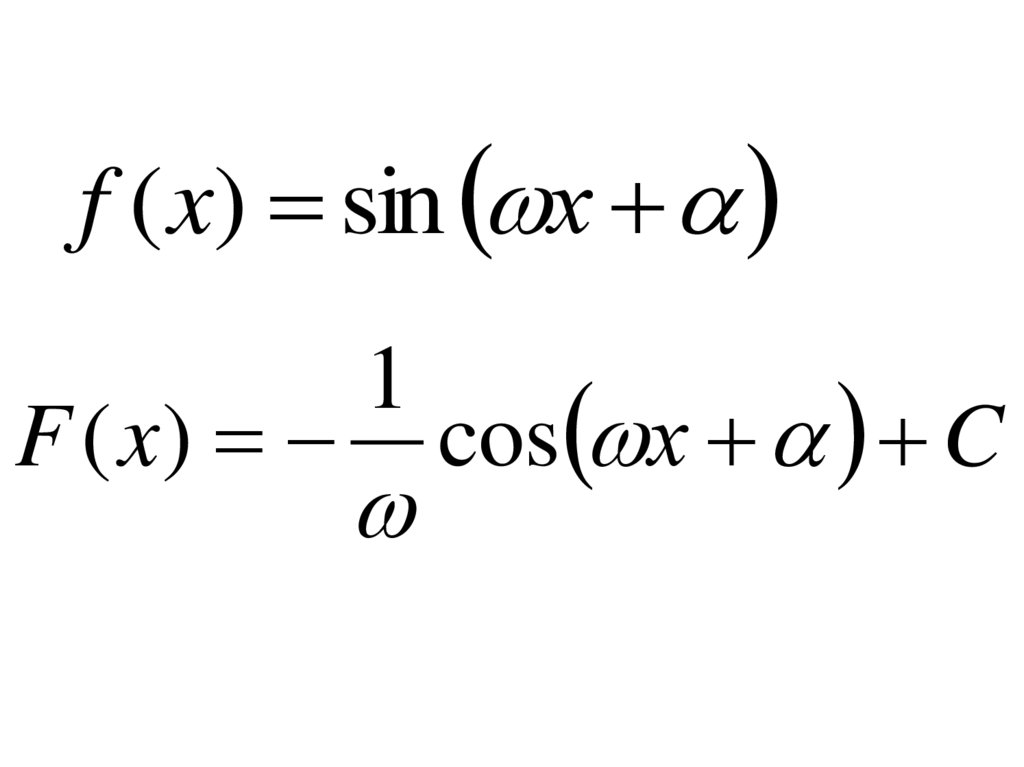
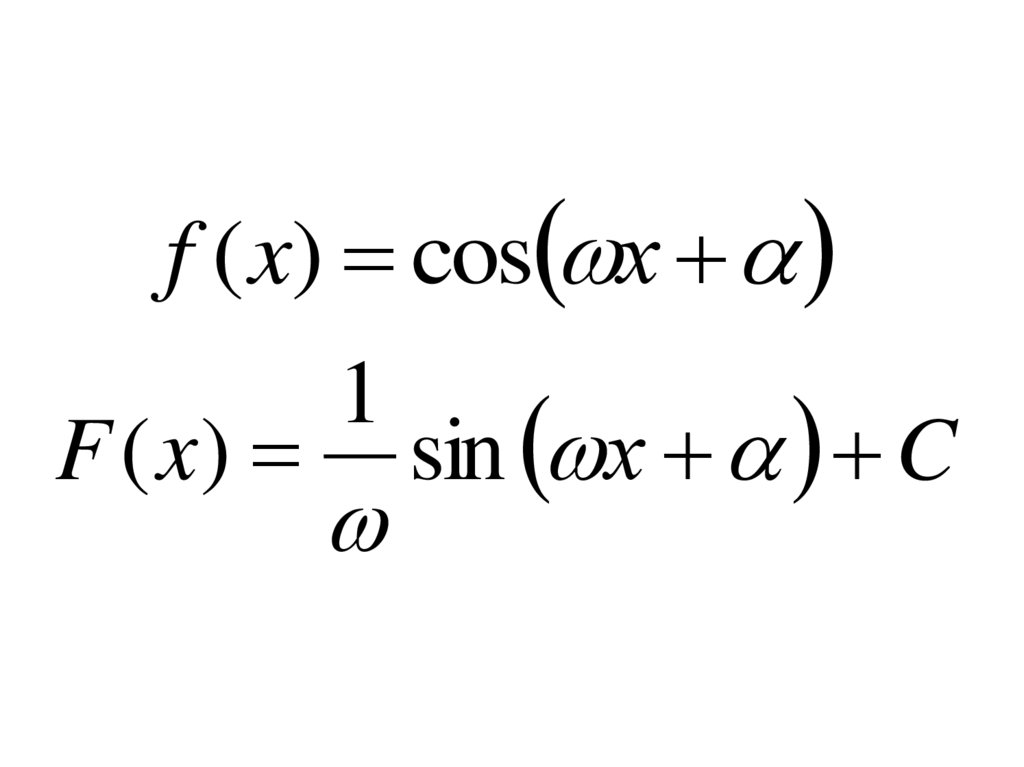



 mathematics
mathematics








