Первообразная. Три правила нахождения первообразной

1.

Первообразная.
Три правила нахождения
первообразной
Выполнила: Котенева К.П.
2020 г

2.

Повторим определение производной
Производной функции в данной точке называется
предел отношения приращения функции в этой
точке к приращению аргумента, когда приращение
аргумента , стремиться к нулю.

3.

Повторим формулы для вычисления производных

4.

Найдите производную
1
сosх
sinх+12

5.

Найдите функцию производная которой равна:

6.

В математике много операций
которые являются обратными
32 = 9

7.

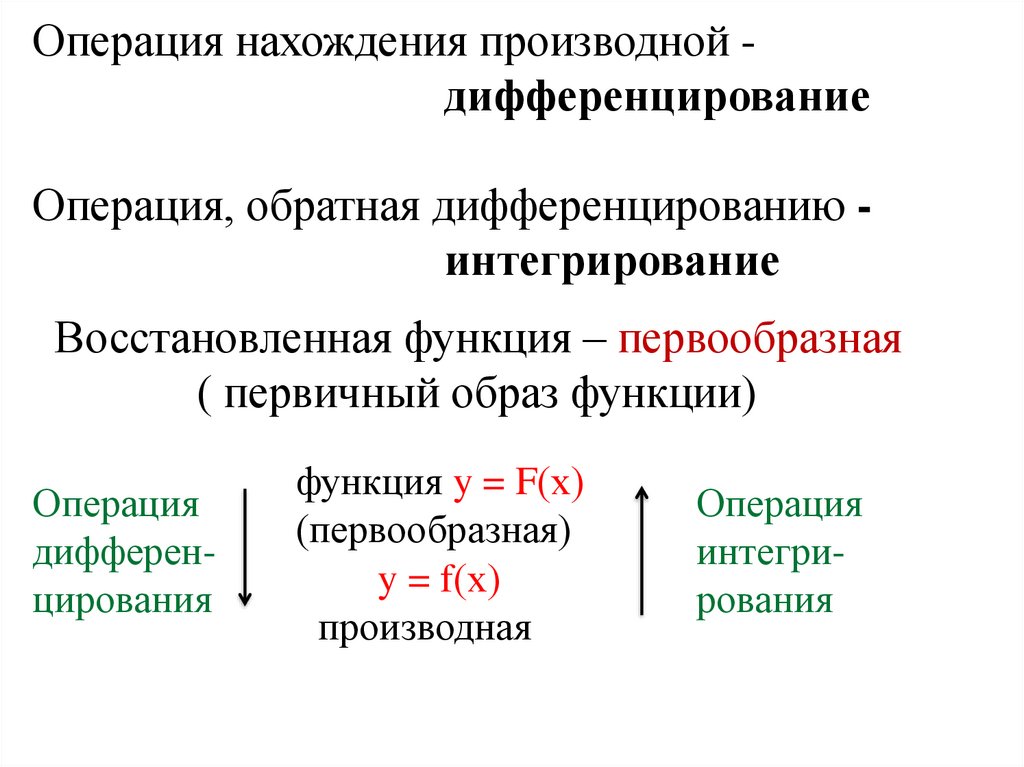
Операция нахождения производной дифференцирование
Операция, обратная дифференцированию интегрирование
Восстановленная функция – первообразная
( первичный образ функции)
Операция
дифференцирования
функция y = F(х)
(первообразная)
y = f(х)
производная
Операция
интегрирования

8.

Определение первообразной
Функция F(x) называется
первообразной для функции f(x)
на заданном промежутке, если
для всех x из этого промежутка
F'(x) = f(x)

9.

Запомните: Первообразная – это родитель
производной:

10.

Основное свойство первообразной
Все первообразные функции f можно записать с
помощью одной формулы, которую называют общим
видом первообразных для функции f.
Любая первообразная для функции f на
промежутке I может быть записана в виде
F(x) + C,
где F(x) – одна из первообразных для функции f(х) на
промежутке I, а С – произвольная постоянная.

11.

Повторение
• Вопрос: какая функция называется
первообразной?
• Ответ: Функция F(x) называется
первообразной функции f(x) на
некотором промежутке, если для всех x
из этого промежутка

12.

Повторение (ответы записать в тетрадь)
• Вопрос 1: как называется процесс
нахождения производной функции?
• Вопрос 2: Каким образом показать,
что
функция
F(x)
является
первообразной для функции f(x)?

13.

Повторение
• Вопрос 3: Является ли функция
F(x)=3x2+11x первообразной для
функции f(x)=6х+10?

14.

С помощью таблицы найдите все первообразные
для функций:
f(x)
F(x)
1
Записать !!!
f(х)=3
f(х)= х2
f(х)=cosx
f(х)=12
f(х)=х5

15.

Три правила нахождения первообразных
Если функции у=f(x) и у=g(x) имеют на
промежутке
первообразные соответственно у=F(x) и у=G(x), то
Функция
Первообразная
у = f(x) + g(x)
у = F(x) + G(x)
у =k f(x)
у =k F(x)

16.

Первое правило интегрирования
Первообразная суммы равна сумме
первообразных
Если F(x)– первообразная для
функции f(x), а G(x)– первообразная
для функции g(x), то F(x)+G(x)–
первообразная
для
функции
f(x)+g(x)

17.

Второе правило интегрирования
Постоянный множитель можно
выносить за знак первообразной
Если F(x)– первообразная для
функции f(x), а а –константа, то
аF(x)–
первообразная
для
функции аf(x)

18.

Третье правило интегрирования
Если F(x) – первообразная для
функции f(x), а k и b- константы,
причем k 0
то
1
F (kx b)
k
-первообразная
для функции f (kx b)

19.

20.

ДЗ найдите все первообразные для функций:
• А) f(x) = 3;
• Б) f(x) =