0братная функция

1.

Обратная функция

2.

Если каждому значению х из некоторого
множества действительных чисел поставлено в
соответствие по определённому правилу
f число у, то, говорят, что на этом множестве
определена функция.
y
y = f(x)
E( f )
0
х
D( f )
x

3.

Если функция у = f ( х ) принимает каждое
своё значение у только при одном значении
х, то эту функцию называют обратимой.
у 2х 2
1
у 2
х
3
у х
у х
х1 у
2
х2 у

4.

Пусть у = f(x) – обратимая функция. Тогда
каждому у из множества значений
функции соответствует одно
определённое число х из области её
определения. Это соответствие
определяет функцию х от у, которую
обозначим х = g(y).
Поменяем местами х и у: у = g(x).
Функцию у = g(x) называют обратной к
функции у = f(x).

5.

1. Область определения обратной функции D(g).
совпадает с множеством значений исходной E(f), а
множество значений обратной функции E(g)
совпадает с областью определения исходной
функции D(f):
D(f ) = E(g), E(f ) = D(g).
2. Монотонная функция является обратимой.
3. График обратной функции симметричен графику
данной функции относительно прямой у = х.

6.

у
у
1
1
0
1
х
0
1
х
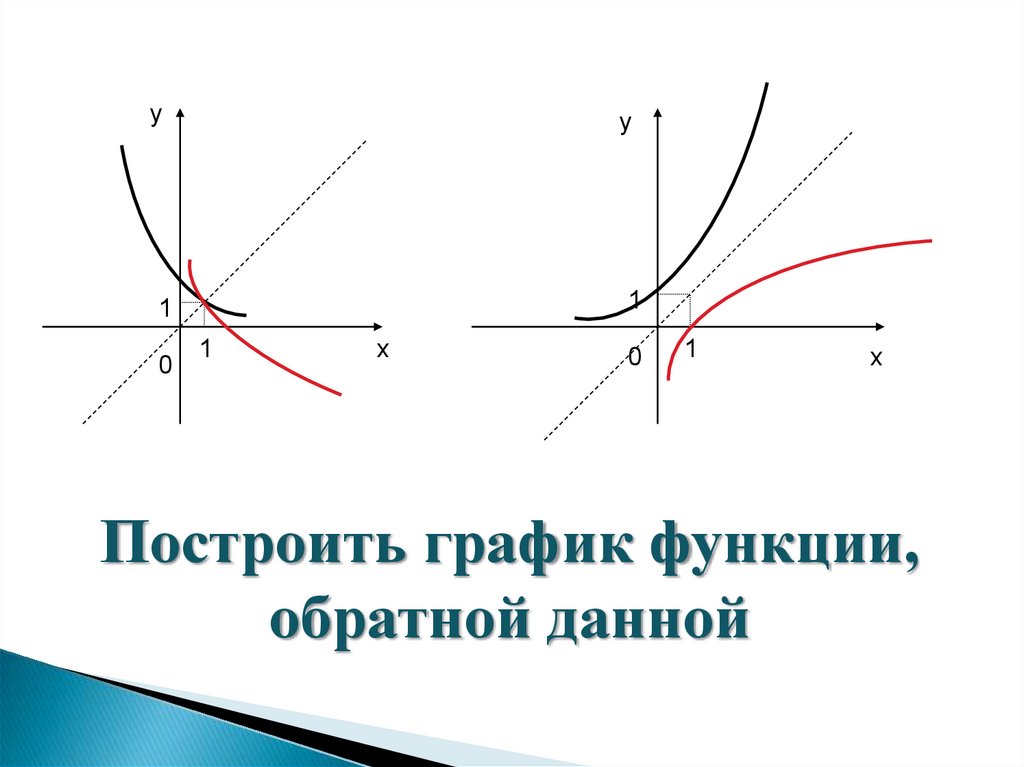
Построить график функции,
обратной данной

7.

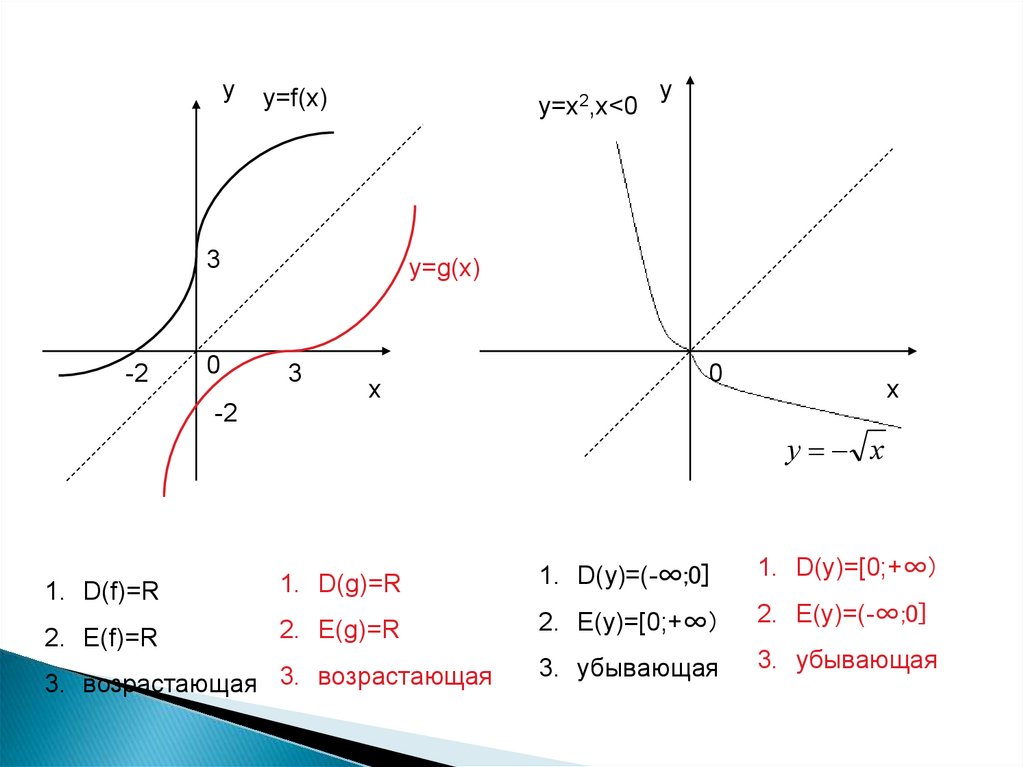
у
у=f(x)
y=x2,х<0
3
-2
0
у
у=g(x)
3
х
0
х
-2
у х
1. D(y)=(-∞;0]
1. D(y)=[0;+∞)
1. D(f)=R
1. D(g)=R
2. E(y)=[0;+∞)
2. E(y)=(-∞;0]
2. E(f)=R
2. E(g)=R
3. убывающая
3. убывающая
3. возрастающая 3. возрастающая

8.

1. Убедиться в монотонности
функции у=f(х). Найти Д(f) и Е(f).
2. Выразить переменную х через у.
у
(х0;у0)
у=х
3. Переобозначить переменные.
(Заменить х на у, у на х).
у0
(у0;х0)
0
х0
х
4. Проверить D(f ) = E(g), E(f ) = D(g).
5. Построить графики и проверить
симметричность относительно
прямой у=х

9. Нахождение формулы функции, обратной к функции y=f(x)

Пример 1
Пример 2

10.

Для заданной функции найдите обратную
функцию и постройте их графики, проверив их
симметричность относительно прямой у= х
у
1) y 2 х 4
у=х
2) y
0
х
х 1

11.

1) y 2 х 4
Д ( у ) R, Е ( у ) R
2х у 4
1
х у 2
2
Обратная
1
у х 2
2
Д ( у ) R, Е ( у ) R
2) y х 1
Д ( у ) 0; , Е ( у ) 1;
х у 1
х у 1
х у 1
2
Обратная
у х 1
2
Д ( у ) 1; , Е ( у ) 0;

12. Установите соответствие между функцией f(x) и обратной к ней функцией g(x)

13. Домашняя работа

1
2
3
4
У=3х-1
У=(2х-1)/3
Y=х2-1
У=(х-1)2
Проверь своё решение