Similar presentations:
Доверительные интервалы
1. Тема. Доверительные интервалы
Доверительный интервал – это интервал, в котором стой или иной заранее заданной вероятностью находится
неизвестный параметр генеральной совокупности.
1. Доверительный интервал для математического
ожидания :
где
S t1 (n 1)
S t1 (n 1)
2
2
x
,
; x
n
n
t
- обратное (квантиль) распределение Стьюдента
2.
2. Доверительный интервал для дисперсии:2
2
S ( n 1) S (n 1)
2
2
; 2
,
(
n
1
)
(
n
1
)
1
2
2
Где
- обратное распределение хи-квадрат
3.
ЗАДАЧА. Получены данные некоторых измерений: 5, 6, 8, 2, 3, 1,1, 4. Записать данные в виде вариационного ряда. Определить
оценки среднего, дисперсии, и стандартного отклонения, а также
построить доверительные интервалы для среднего и дисперсии на
уровне значимости =0,05.
Решение
вариационный ряд: 1, 1, 2, 3, 4, 5, 6, 8.
1
x (1 1 2 3 4 5 6 8) 3,75.
8
1 2 2 2 2 2 2 2 2
1 1 2 3 4 5 6 8 8 3,752 6,214.
S
8 1
2
Стандартное отклонение
S S 2 2,493
4.
S t1 (n 1)S t1 (n 1)
2
2
x
,
; x
n
n
.
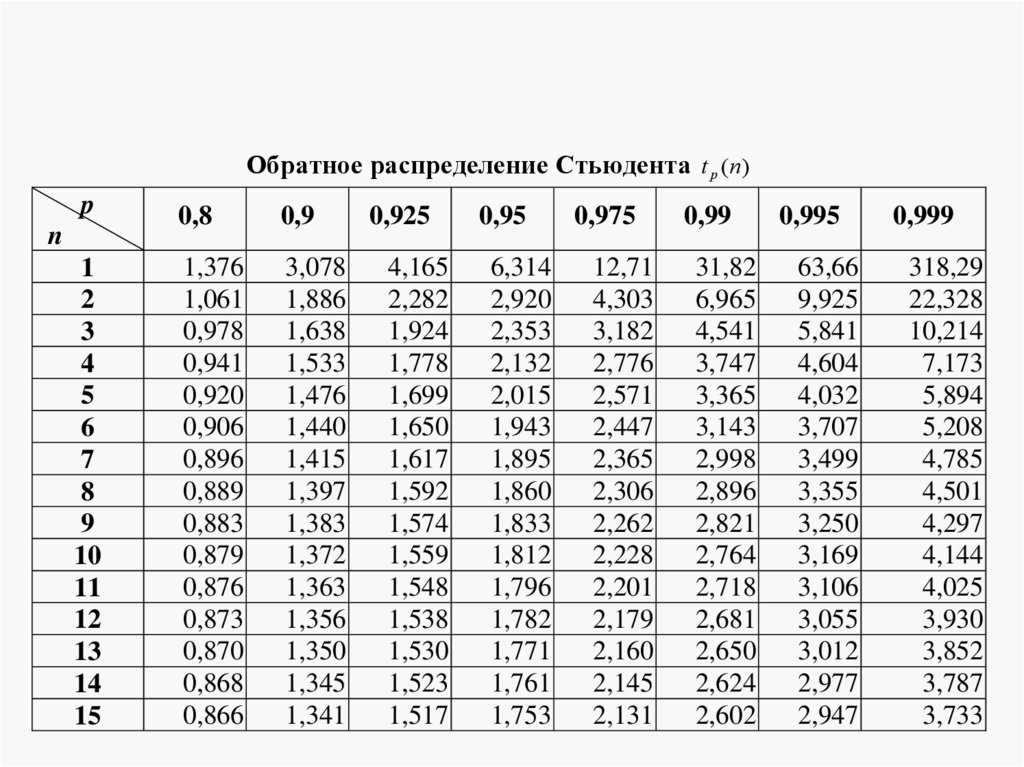
t1 0,05 / 2 (8 1) t0,975 (7) 2,365
Получаем доверительный интервал
для математического ожидания
2,493 2,365
2,493 2,365
; 3,75
3,75
8
8
или
1,665;
5,835
5.
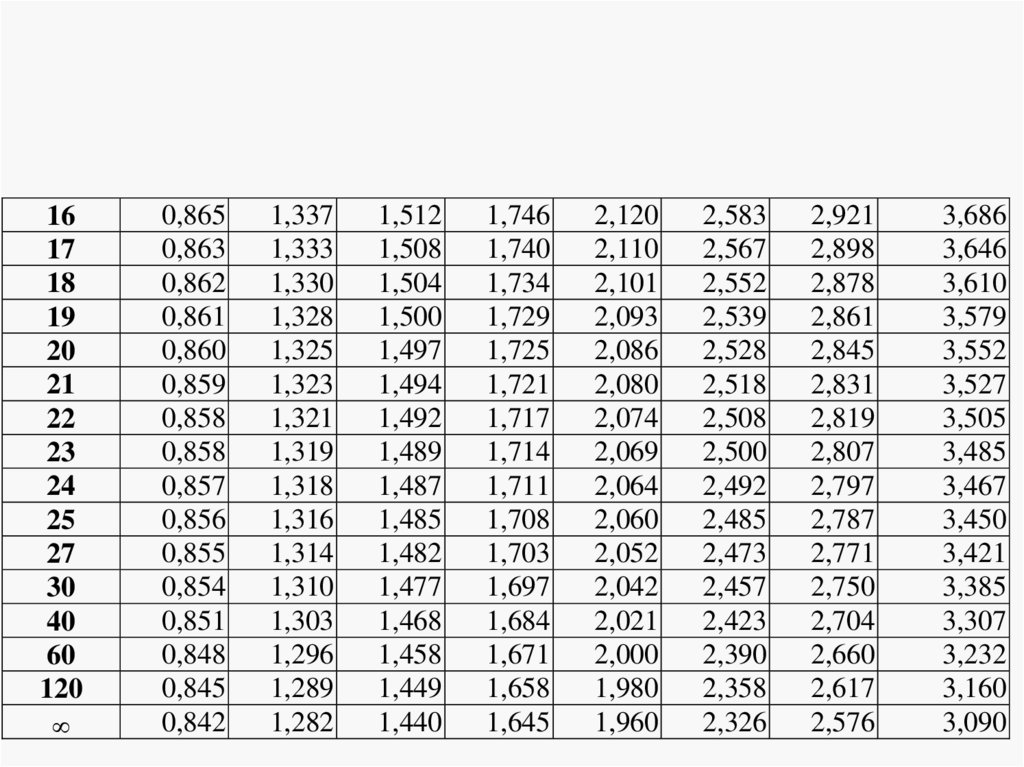
Обратное распределение Стьюдента t p (n)p
0,8
0,9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1,376
1,061
0,978
0,941
0,920
0,906
0,896
0,889
0,883
0,879
0,876
0,873
0,870
0,868
0,866
3,078
1,886
1,638
1,533
1,476
1,440
1,415
1,397
1,383
1,372
1,363
1,356
1,350
1,345
1,341
n
0,925
4,165
2,282
1,924
1,778
1,699
1,650
1,617
1,592
1,574
1,559
1,548
1,538
1,530
1,523
1,517
0,95
6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1,812
1,796
1,782
1,771
1,761
1,753
0,975
12,71
4,303
3,182
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,201
2,179
2,160
2,145
2,131
0,99
31,82
6,965
4,541
3,747
3,365
3,143
2,998
2,896
2,821
2,764
2,718
2,681
2,650
2,624
2,602
0,995
63,66
9,925
5,841
4,604
4,032
3,707
3,499
3,355
3,250
3,169
3,106
3,055
3,012
2,977
2,947
0,999
318,29
22,328
10,214
7,173
5,894
5,208
4,785
4,501
4,297
4,144
4,025
3,930
3,852
3,787
3,733
6.
1617
18
19
20
21
22
23
24
25
27
30
40
60
120
0,865
0,863
0,862
0,861
0,860
0,859
0,858
0,858
0,857
0,856
0,855
0,854
0,851
0,848
0,845
0,842
1,337
1,333
1,330
1,328
1,325
1,323
1,321
1,319
1,318
1,316
1,314
1,310
1,303
1,296
1,289
1,282
1,512
1,508
1,504
1,500
1,497
1,494
1,492
1,489
1,487
1,485
1,482
1,477
1,468
1,458
1,449
1,440
1,746
1,740
1,734
1,729
1,725
1,721
1,717
1,714
1,711
1,708
1,703
1,697
1,684
1,671
1,658
1,645
2,120
2,110
2,101
2,093
2,086
2,080
2,074
2,069
2,064
2,060
2,052
2,042
2,021
2,000
1,980
1,960
2,583
2,567
2,552
2,539
2,528
2,518
2,508
2,500
2,492
2,485
2,473
2,457
2,423
2,390
2,358
2,326
2,921
2,898
2,878
2,861
2,845
2,831
2,819
2,807
2,797
2,787
2,771
2,750
2,704
2,660
2,617
2,576
3,686
3,646
3,610
3,579
3,552
3,527
3,505
3,485
3,467
3,450
3,421
3,385
3,307
3,232
3,160
3,090
7.
22
S ( n 1) S (n 1)
2
,
; 2
2
1 ( n 1) (n 1)
2
2
2
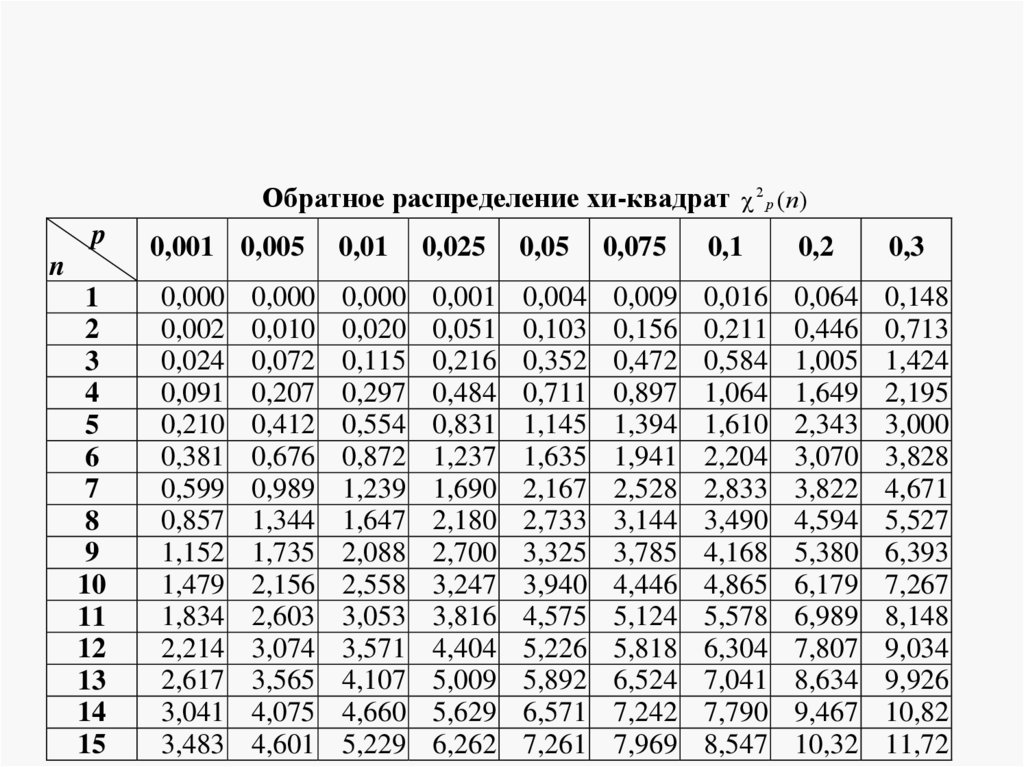
1 0 , 05 / 2
(8 1) 16,0;
2
0 , 05 / 2
(8 1) 1,69.
7 6,214 7 6,214
;
1,69
16
(2,719; 25,738)
8.
Обратное распределение хи-квадрат 2 p (n)p
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0,001 0,005
0,000
0,002
0,024
0,091
0,210
0,381
0,599
0,857
1,152
1,479
1,834
2,214
2,617
3,041
3,483
0,000
0,010
0,072
0,207
0,412
0,676
0,989
1,344
1,735
2,156
2,603
3,074
3,565
4,075
4,601
0,01
0,000
0,020
0,115
0,297
0,554
0,872
1,239
1,647
2,088
2,558
3,053
3,571
4,107
4,660
5,229
0,025
0,001
0,051
0,216
0,484
0,831
1,237
1,690
2,180
2,700
3,247
3,816
4,404
5,009
5,629
6,262
0,05
0,004
0,103
0,352
0,711
1,145
1,635
2,167
2,733
3,325
3,940
4,575
5,226
5,892
6,571
7,261
0,075
0,009
0,156
0,472
0,897
1,394
1,941
2,528
3,144
3,785
4,446
5,124
5,818
6,524
7,242
7,969
0,1
0,2
0,3
0,016
0,211
0,584
1,064
1,610
2,204
2,833
3,490
4,168
4,865
5,578
6,304
7,041
7,790
8,547
0,064
0,446
1,005
1,649
2,343
3,070
3,822
4,594
5,380
6,179
6,989
7,807
8,634
9,467
10,32
0,148
0,713
1,424
2,195
3,000
3,828
4,671
5,527
6,393
7,267
8,148
9,034
9,926
10,82
11,72
9.
Обратное распределение хи-квадрат 2 p (n)p
n
16
17
18
19
20
21
22
23
24
25
27
30
40
50
75
100
200
0,001 0,005
0,01
0,025
0,05
3,942
4,416
4,905
5,407
5,921
6,447
6,983
7,529
8,085
8,649
9,803
11,59
17,92
24,67
42,76
61,92
143,8
5,812
6,408
7,015
7,633
8,260
8,897
9,542
10,20
10,86
11,52
12,88
14,95
22,16
29,71
49,48
70,06
156,4
6,908
7,564
8,231
8,907
9,591
10,28
10,98
11,69
12,40
13,12
14,57
16,79
24,43
32,36
52,94
74,22
162,7
7,962
8,672
9,390
10,12
10,85
11,59
12,34
13,09
13,85
14,61
16,15
18,49
26,51
34,76
56,05
77,93
168,3
5,142
5,697
6,265
6,844
7,434
8,034
8,643
9,260
9,886
10,52
11,81
13,79
20,71
27,99
47,21
67,33
152,2
0,075
8,707
9,452
10,21
10,97
11,73
12,50
13,28
14,07
14,85
15,65
17,24
19,66
27,93
36,40
58,15
80,41
172,0
0,1
0,2
0,3
9,312
10,09
10,87
11,65
12,44
13,24
14,04
14,85
15,66
16,47
18,11
20,60
29,05
37,69
59,79
82,36
174,8
11,15
12,00
12,86
13,72
14,58
15,44
16,31
17,19
18,06
18,94
20,71
23,36
32,34
41,45
64,55
87,95
183,0
12,62
13,53
14,44
15,35
16,27
17,18
18,10
19,02
19,94
20,87
22,72
25,51
34,87
44,31
68,13
92,13
189,0
10.
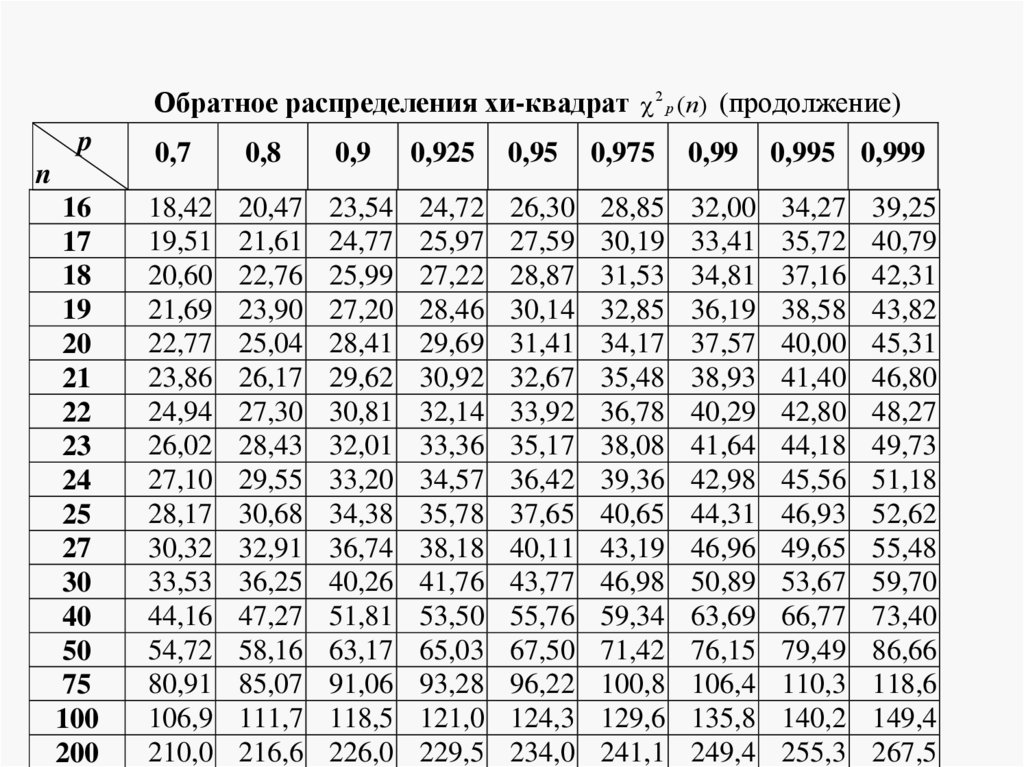
Обратное распределения хи-квадрат 2 p (n) (продолжение)p
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0,7
0,8
0,9
1,074
2,408
3,665
4,878
6,064
7,231
8,383
9,524
10,66
11,78
12,90
14,01
15,12
16,22
17,32
1,642
3,219
4,642
5,989
7,289
8,558
9,803
11,03
12,24
13,44
14,63
15,81
16,98
18,15
19,31
2,706
4,605
6,251
7,779
9,236
10,64
12,02
13,36
14,68
15,99
17,28
18,55
19,81
21,06
22,31
0,925
3,170
5,181
6,905
8,496
10,01
11,47
12,88
14,27
15,63
16,97
18,29
19,60
20,90
22,18
23,45
0,95
3,841
5,991
7,815
9,488
11,07
12,59
14,07
15,51
16,92
18,31
19,68
21,03
22,36
23,68
25,00
0,975
5,024
7,378
9,348
11,14
12,83
14,45
16,01
17,53
19,02
20,48
21,92
23,34
24,74
26,12
27,49
0,99
6,635
9,210
11,35
13,28
15,09
16,81
18,48
20,09
21,67
23,21
24,73
26,22
27,69
29,14
30,58
0,995 0,999
7,879
10,60
12,84
14,86
16,75
18,55
20,28
21,95
23,59
25,19
26,76
28,30
29,82
31,32
32,80
10,83
13,82
16,27
18,47
20,51
22,46
24,32
26,12
27,88
29,59
31,26
32,91
34,53
36,12
37,70
11.
Обратное распределения хи-квадрат 2 p (n) (продолжение)p
0,7
0,8
0,9
16
17
18
19
20
21
22
23
24
25
27
30
40
50
75
100
200
18,42
19,51
20,60
21,69
22,77
23,86
24,94
26,02
27,10
28,17
30,32
33,53
44,16
54,72
80,91
106,9
210,0
20,47
21,61
22,76
23,90
25,04
26,17
27,30
28,43
29,55
30,68
32,91
36,25
47,27
58,16
85,07
111,7
216,6
23,54
24,77
25,99
27,20
28,41
29,62
30,81
32,01
33,20
34,38
36,74
40,26
51,81
63,17
91,06
118,5
226,0
n
0,925
24,72
25,97
27,22
28,46
29,69
30,92
32,14
33,36
34,57
35,78
38,18
41,76
53,50
65,03
93,28
121,0
229,5
0,95
26,30
27,59
28,87
30,14
31,41
32,67
33,92
35,17
36,42
37,65
40,11
43,77
55,76
67,50
96,22
124,3
234,0
0,975
28,85
30,19
31,53
32,85
34,17
35,48
36,78
38,08
39,36
40,65
43,19
46,98
59,34
71,42
100,8
129,6
241,1
0,99
32,00
33,41
34,81
36,19
37,57
38,93
40,29
41,64
42,98
44,31
46,96
50,89
63,69
76,15
106,4
135,8
249,4
0,995 0,999
34,27
35,72
37,16
38,58
40,00
41,40
42,80
44,18
45,56
46,93
49,65
53,67
66,77
79,49
110,3
140,2
255,3
39,25
40,79
42,31
43,82
45,31
46,80
48,27
49,73
51,18
52,62
55,48
59,70
73,40
86,66
118,6
149,4
267,5
12.
Статистическая погрешность- это половина длины доверительного интервала
Если объем генеральной совокупности велик или
не известен, то
S t1 (n 1)
x
2
n
Если генеральная совокупность имеет объем N, то
x
S t1 (n 1)
2
n
n
1
N
13.
ЗАДАЧА. Школьному психологу необходимо определитьсредний уровень вербальной памяти у первоклассников. Для этого были
случайно отобраны 19 школьников и по результатам тестов вычислены
выборочное среднее и дисперсия вербальной памяти, которые равны,
соответственно 21,36 и 11,04. Найти статистическую погрешность на
уровне значимости α = 0,05, если:
а) психолога интересует средний уровень вербальной памяти
всех первоклассников региона;
б) психолога интересует средний уровень памяти учеников
данной школы, в которой 58 первоклассников.
14.
Решение. Имеемx 21,36; S 2 11,04; n 19; S 11,04 3,32.
По таблице ПРИЛОЖЕНИЯ находим
t1 0,05 (19 1) t 0,975 (18) 2,101 . Отсюда
2
а) если объем генеральной совокупности велик, то
x
3,32 2,101
19
41,6
,36 ;
б) если объем генеральной совокупности равен N = 58, то
x
3,32 2,101
19
19
1
1,31
2,15 .
58
15.
Статистическая погрешность частотыравна
w
w(1 w)
t1 (n 1)
2
n
если объем генеральной совокупности велик
или не известен, и
w
w(1 w)
n
1 t1 (n 1)
2
n
N
если генеральная совокупность имеет объем
N.
16.
..
ЗАДАЧА. Психологу крупной торговой
сети необходимо определить
долю экстравертов среди менеджеров. Для этого были случайно отобраны
и протестированы 35 менеджера и выяснилось, что среди них 18
экстравертов. Определить долю экстравертов и ее статистическую
погрешность на уровне значимости =0,02, если а) число менеджеров в
торговой сети велико; б) число менеджеров равно 80.
Решение.
Частота (доля экстравертов) равна w=18/35=0,514. По таблице находим
t1 0,02 (35 1) t0,99 (34) 2,45
2
Отсюда, если а) число менеджеров в торговой сети велико, то
w
w(1 w)
t1 (n 1)
2
n
w
0,514(1 0,514)
2,45 0,2
35
б) число менеджеров равно 80, то
w
w(1 w)
n
1 t1 (n 1)
2
n
N
0,514(1 0,514)
35
w
1 2,45 0,15
35
80
17.
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗСтатистической гипотезой называется некоторое предположение, которое
принимается или отвергается на основании статистических данных.
- нулевая гипотеза
- альтернативная гипотеза
α - уровень значимости (0,01-0,1). Это вероятность того, что
отвергнута верная нулевая гипотеза)
- доверительная вероятность
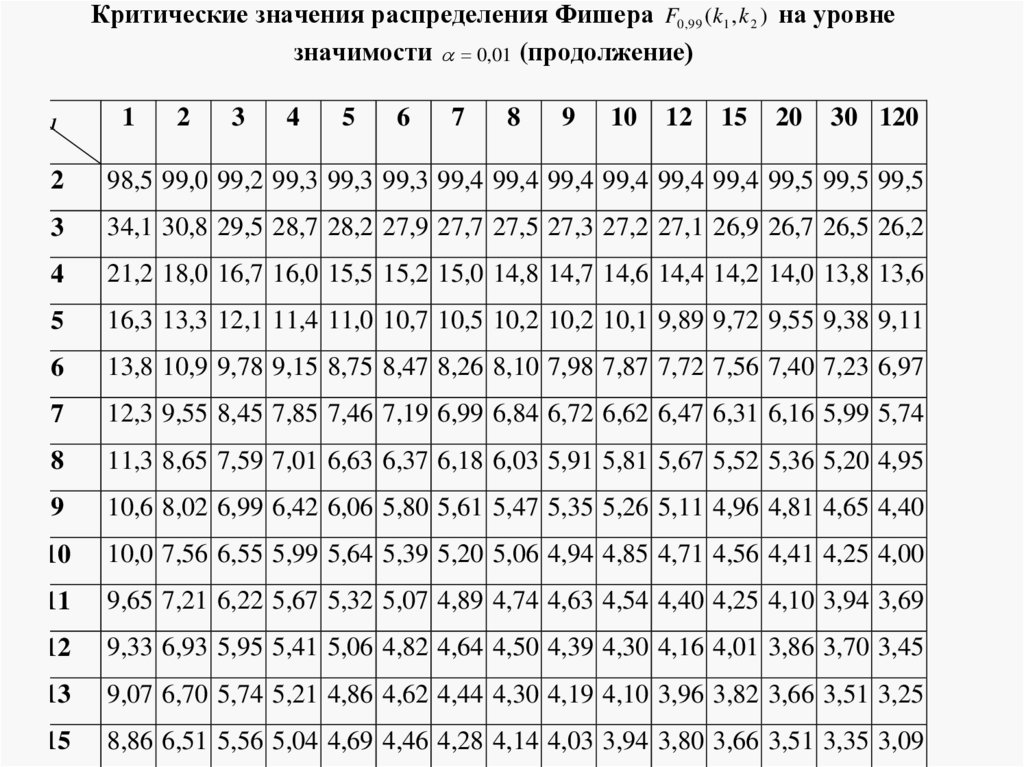
Критерий согласия Пирсона (критерий χ – квадрат).
Пусть имеется несколько показателей
Типичные значения (норма) показателей
Экспериментальные значения (норма) показателей
зависит от двух значений: доверительной вероятности
α и числа
называемого числом степеней свободы.
Если
, то предположение о том, что опытные данные соответствуют
нормам, принимается.
18.
ЗАДАЧА. Для формирования профильных классов ученикичетвертого класса проходят профориентационный тест на выявление
способностей к тем или иным наукам. Согласно городской
статистики,
учащихся четвертых классов имеют склонность к
гуманитарным наукам,
– к математическим,
– к
естественным,
– не определена.
При проверке 62 школьников данной школы оказалось, что имеют
склонность к гуманитарным наукам – 21 человек, к математическим
– 17 человек, к естественным – 14 человек и не выявили склонность
10 человек. Можно ли с вероятностью
считать, что
профориентационное распределение четвероклассников в данной
школе соответствует городскому.
19.
Решение.Записываем школьные показатели профориентации во вторую строчку
расчетной таблицы. Согласно городской статистики из 62 школьников
склонность к гуманитарным наукам должны проявлять (нормы) 62 32%
= 19,84 школьника, к математическим – 62 27% = 16,74 школьника, к
естественным – 62 25% = 15,5 школьника и не выявили склонность
62 16% = 9,92 школьника. Эти нормы записываем в третью строчку
расчетной таблицы. В следующую строку записываем значения
критерия, получаем таблицу вида:
Способнос Гуманитар Математиче Естественн Не выявлены
ти
ные науки ские науки
ые науки
21
17
14
10
19,84
16,74
15,5
9,92
0,068
0,004
0,145
0,0645
По таблице критических значений (ПРИЛОЖЕНИЕ )
следовательно, основная гипотеза принимается, то
есть распределение способностей в классах
соответствует городскому
20.
Проверка гипотез о равенстведисперсий
1. Получают выборку показателя в двух группах объемом




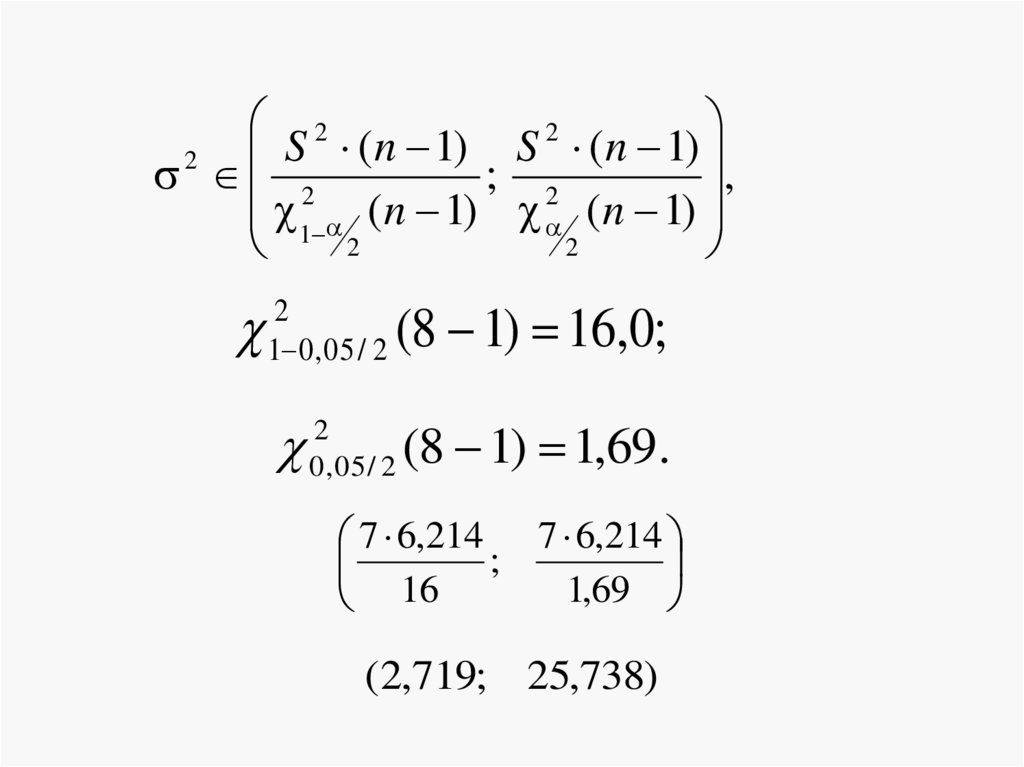















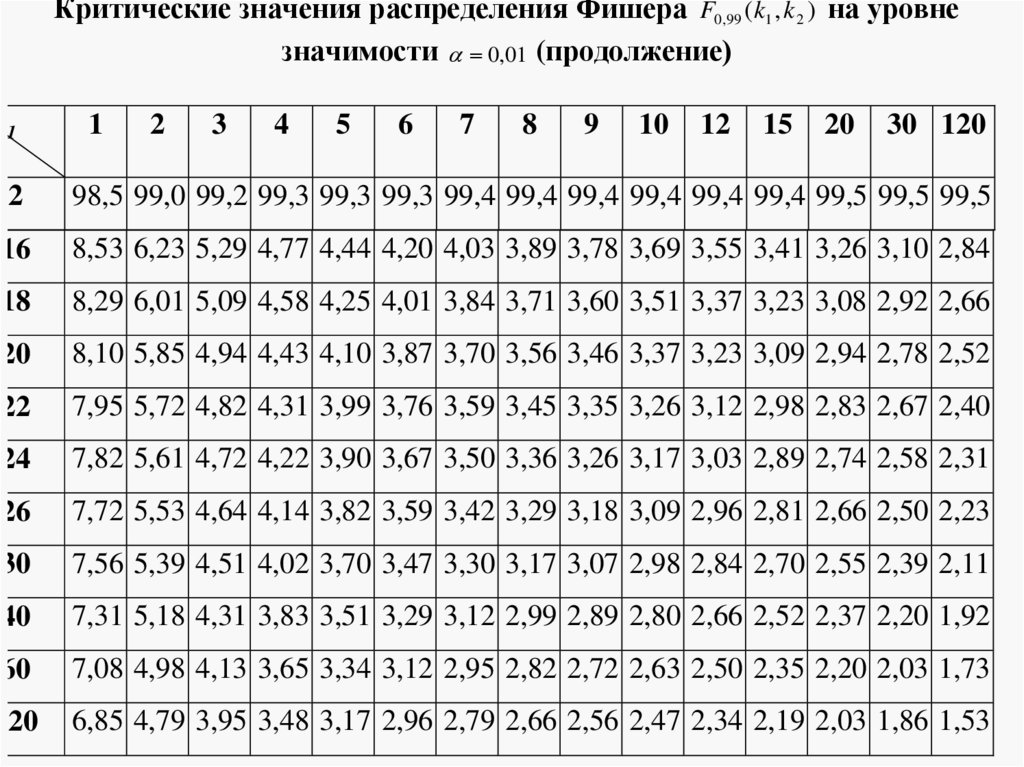
 mathematics
mathematics








