Доверительные интервалы. Расчет репрезентативного объема выборки. Лекция 8

1. ЛЕКЦИЯ 8

ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ.
РАСЧЕТ РЕПРЕЗЕНТАТИВНОГО
ОБЪЕМА ВЫБОРКИ

2. Алгоритм оценки разницы между двумя группами:

Формулируется H0: обе группы – две
случайные выборки из одной
совокупности;
Оценивается вероятность получить
наблюдаемые различия при
условии, что H0 верна.
Если полученная вероятность P < α,
то принимается HA (= «установлены
статистически значимые различия
между группами»)

3. Доверительный интервал

Истинное среднее при
нормальном распределении
в 95% случаев попадает
в интервал: среднее ± 2
стандартных ошибки среднего
Sx
x

4. Суть «доверительного интервала» (confidence interval)

Не зная точно, чему равна
некоторая величина, мы с
заданной вероятностью можем
указать диапазон значений,
в котором она находится.

5. 8.1. Доверительный интервал для разности средних и долей

6. t-критерий Стьюдента

x1 x2
t
s x1 x2
Если |t| > tα, то HA

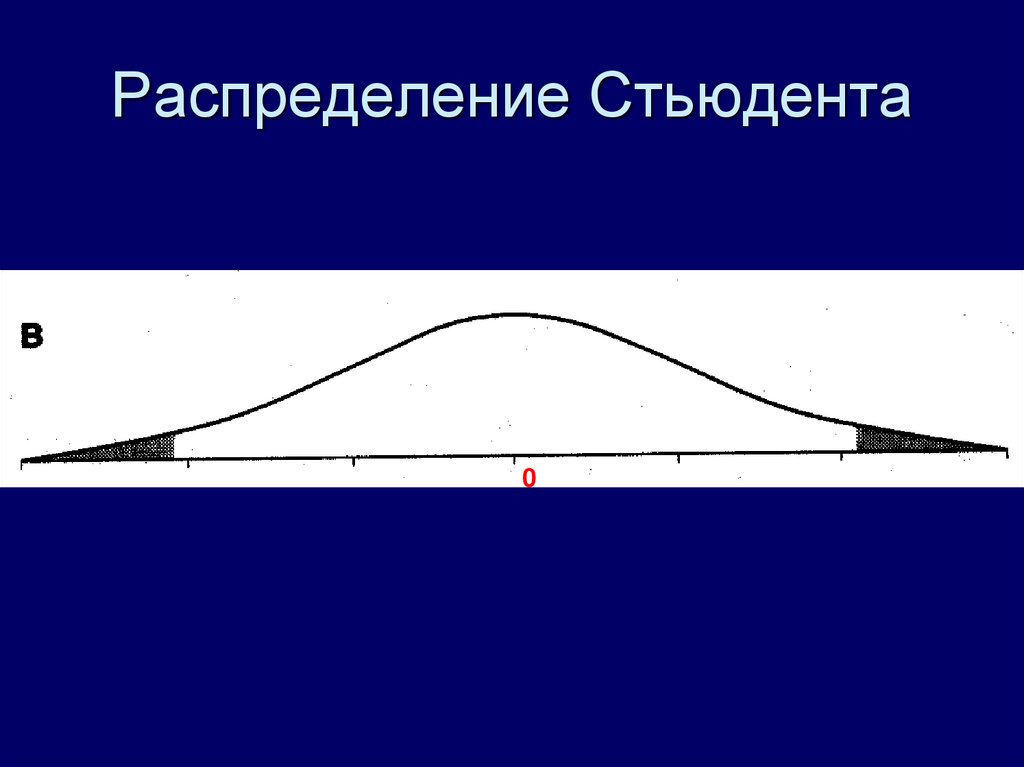
7. Распределение Стьюдента

0

8. Поправка, благодаря которой распределение t всегда будет симметрично относительно 0

( x1 x2 ) ( 1 2 )
t
s x1 x2

9. Свойства t-распределения :

100α % всех возможных
значений t расположены
левее -tα или правее +tα ;
Остальные 100(1 – α) %
значений t попадают в
интервал от -tα до +tα

10. …т.е. в 100(1 – α) % всех случаев мы имеем:

( x1 x2 ) ( 1 2 )
t
t
sx1 x2

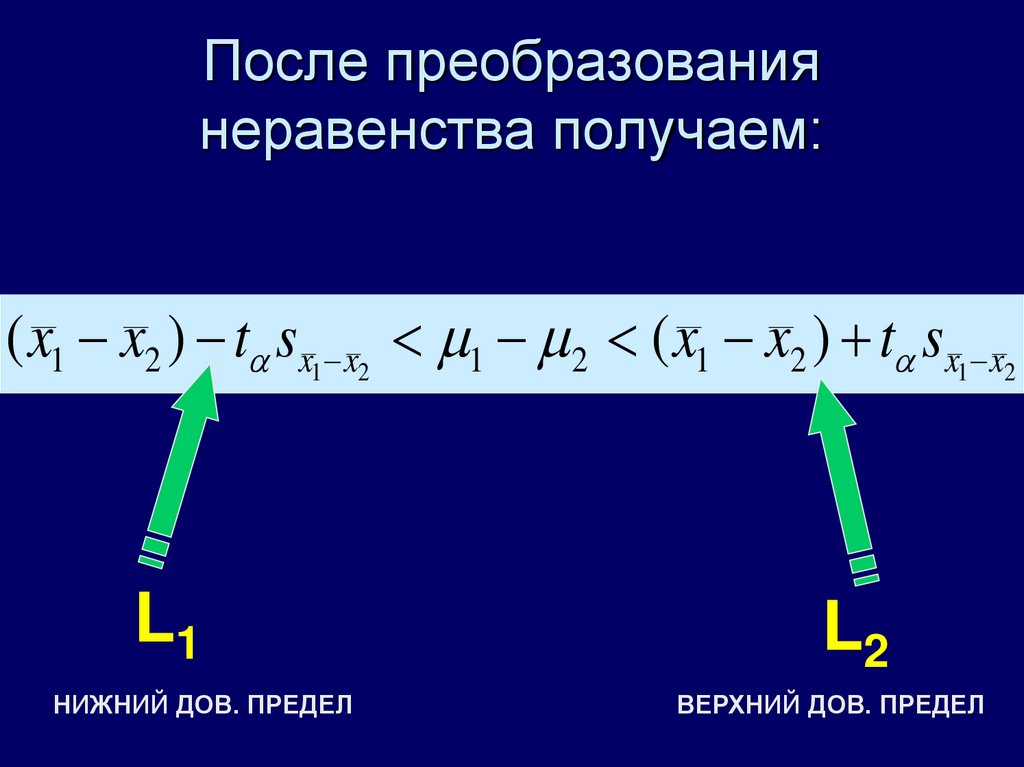
11. После преобразования неравенства получаем:

( x1 x2 ) t sx1 x2 1 2 ( x1 x2 ) t sx1 x2
L1
НИЖНИЙ ДОВ. ПРЕДЕЛ
L2
ВЕРХНИЙ ДОВ. ПРЕДЕЛ

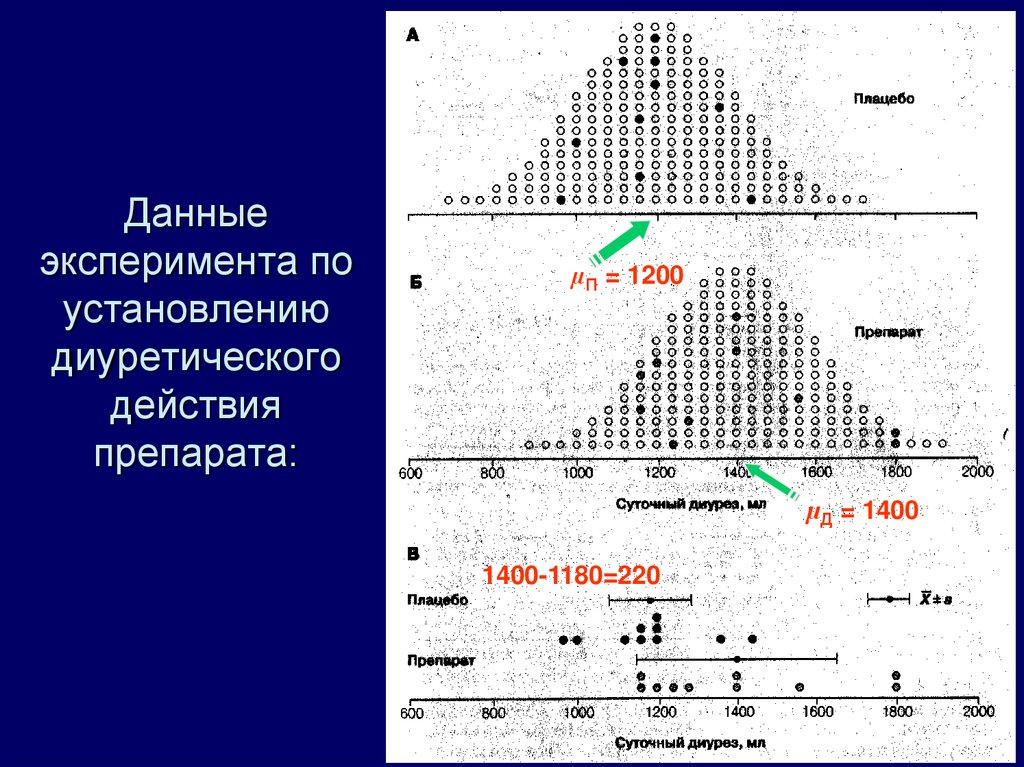
12. Данные эксперимента по установлению диуретического действия препарата:

µП = 1200
µД = 1400
1400-1180=220

13. Расчет 95% доверительного интервала:

Стандартные отклонения у принимавших
диуретик и плацебо составили
соответственно 245 мл и 144 мл
стандартная ошибка разности средних =
89.9
df = 2(n – 1) = 2(10 – 1) = 18 t0,05 = 2,101
( x Д xП ) t0,05sx Д xП 1 2 ( x Д xП ) t0,05sx Д xП
Доверительный интервал:
220 – 2,101 89,9 < µД - µП < 220 + 2,101
89,9
и окончательно: 31 < µД - µП < 409

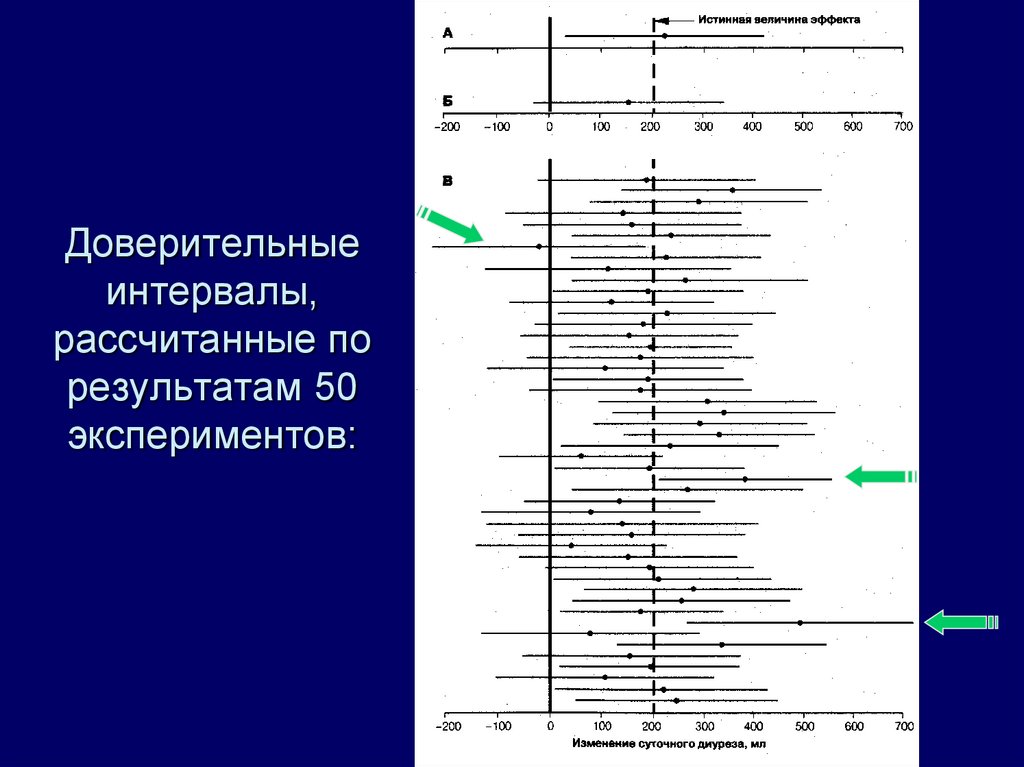
14. Доверительные интервалы, рассчитанные по результатам 50 экспериментов:

15. z-критерий – аналог критерия Стьюдента

pˆ1 pˆ 2
z
s pˆ1 pˆ 2

16. 100(1 – α)-процентный интервал для разности истинных долей:

( pˆ1 pˆ 2 ) z s pˆ1 pˆ 2 p1 p2 ( pˆ1 pˆ 2 ) z s pˆ1 pˆ 2

17. 8.2. Доверительный интервал для средней арифметической и доли

18.

Поскольку
( x1 x2 ) ( 1 2 )
t
s x1 x2
подчиняется распределению
Стьюдента, то и величина
x
t
sx
имеет то же распределение

19. 100(1 – α)-процентный доверительный интервал для средней арифметической:

x t sx x t sx

20. 100(1 – α)-процентный доверительный интервал для доли:

pˆ t s pˆ p pˆ t s pˆ

21. Следует помнить!!!

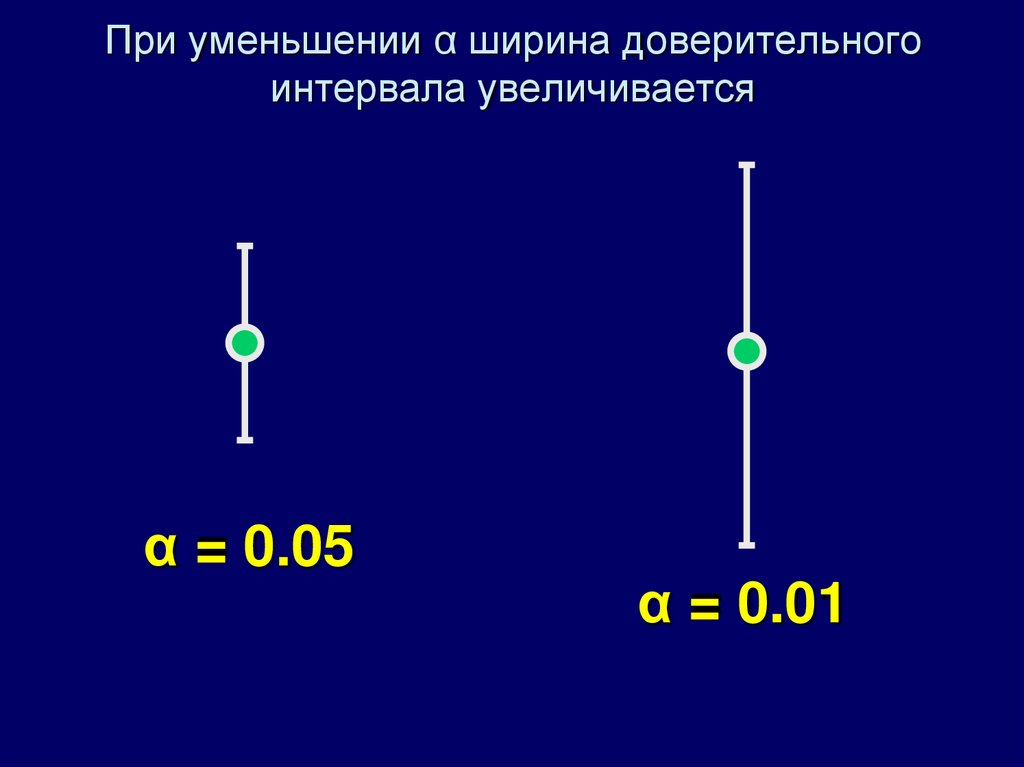
При снижении уровня значимости
(например, с 0.05 до 0.01)
доверительный интервал
расширяется, т.к.
увеличивается
соответствующее
критическое значение t.

22. При уменьшении α ширина доверительного интервала увеличивается

α = 0.05
α = 0.01

23. 8.3. Проверка гипотез с помощью доверительных интервалов

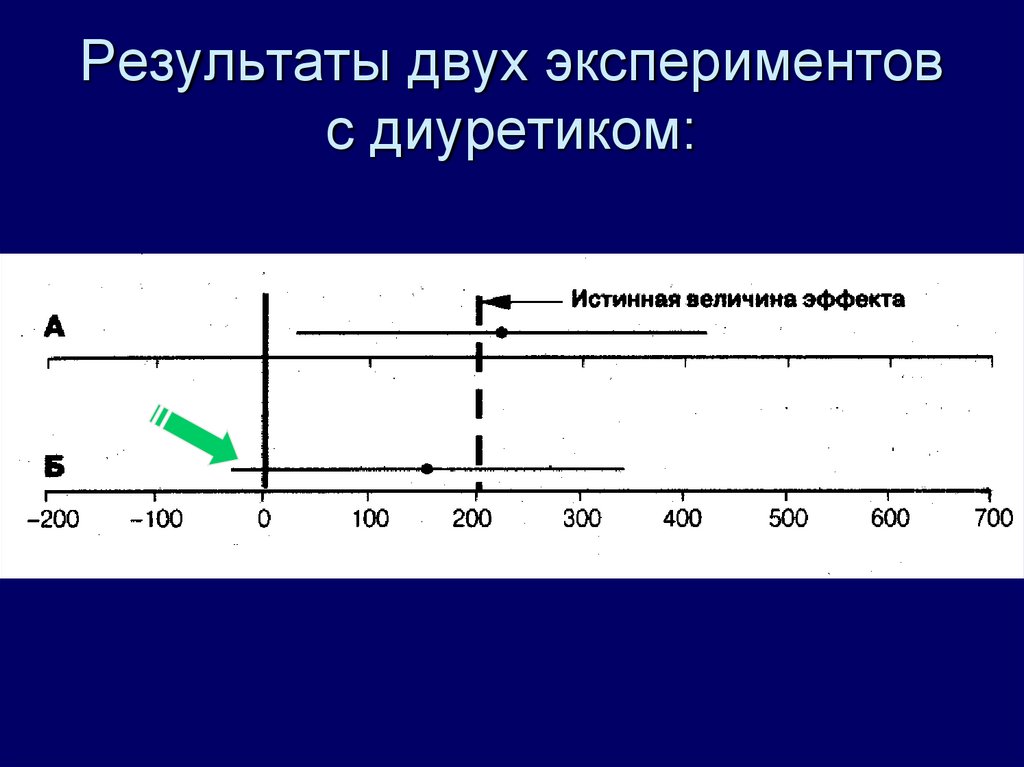
24. Правило:

Если 100(1 – α)-процентный
интервал разности средних не
содержит 0, то различия
статистически значимы (P < α);
напротив, если этот интервал
содержит 0, то различия
статистически не значимы (P > α).

25. Результаты двух экспериментов с диуретиком:

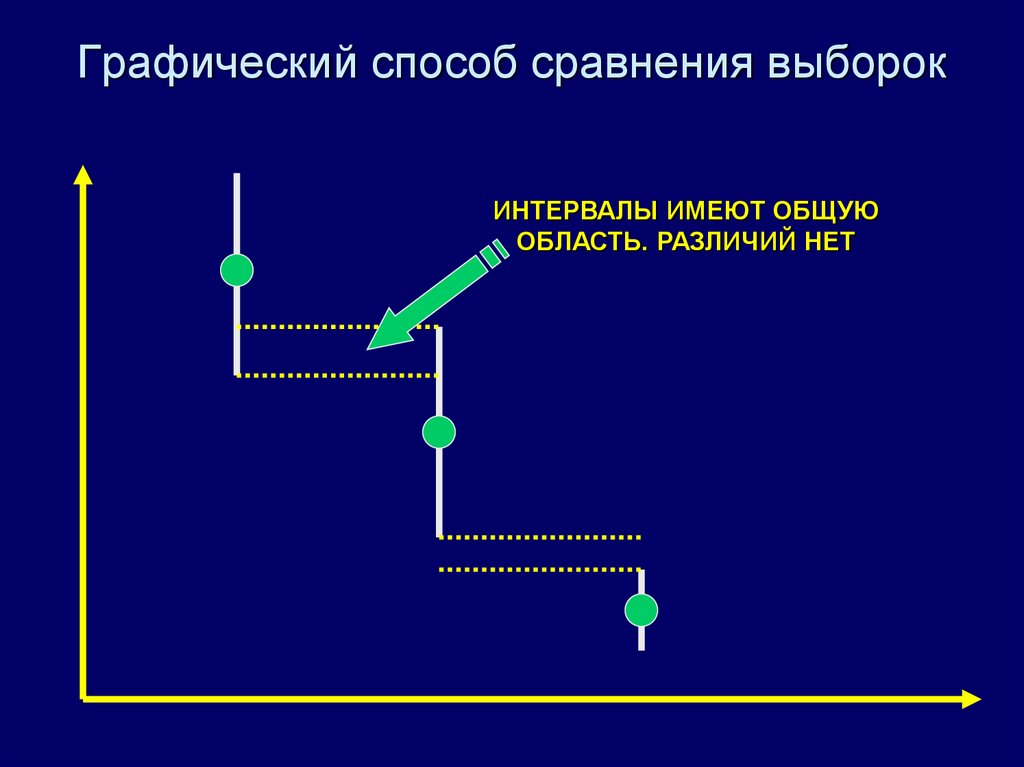
26. Графический способ сравнения выборок

ИНТЕРВАЛЫ ИМЕЮТ ОБЩУЮ
ОБЛАСТЬ. РАЗЛИЧИЙ НЕТ

27. 8.4. Расчет репрезентативного объема выборки

28. Сколько выполнять наблюдений?

Неразумно стремиться к
выполнению неоправданно
большого числа
наблюдений!

29. Как определить «оптимальный» объем выборки???

2 2
n
t s
2
, где
tsx

30. Пример определения необходимого объема выборки:

В ходе 15 взвешиваний крыс был
получен средний вес 100 г.
Стандартная ошибка средней
составила 9 г.
Вопрос: какое количество наблюдений
необходимо выполнить, чтобы
уменьшить ошибку средней вдвое?

31. Пример определения необходимого объема выборки:

1.96 * (9 / 2) 8.82 77.8
2
s
поскольку s x
, то
n
s sx n 9 * 15 34.9 ; отсюда
2
2
(1.96) (34.9)
n
60
77.8

32. Правило:

Чтобы уменьшить ошибку
выборочной средней в К
раз, объем выборки нужно
увеличить в К2 раз.

33. Определение необходимого объема выборки при качественной вариации:

t p(1 p)
n
2
, или
2
t p(100 p)
n
2
2