Элементы теории вероятностей и статистики. Решение задач на доверительные интервалы

1. Тема 1. Элементы теории вероятностей и статистики Решение задач на доверительные интервалы

2.

Интервальные оценки параметров
Выборочные оценки параметров являются СВ.
На основании выборочных оценок можно установить
интервалы, внутри которых с некоторой вероятностью
находятся истинные значения параметров.
Интервальной оценкой параметра θ называется
интервал (θ1, θ2), который с заданной вероятностью
накрывает неизвестное значение параметра.
Интервал (θ1, θ2) называется доверительным
интервалом, а вероятность – доверительной
вероятностью (надежность. доверительного интервала).
Вероятность 1 называется уровнем
значимости.

3.

Интервальные оценки параметров
P 1 2 1
P 1 P 2 / 2
1 0,1; 0,05; 0,01

4.

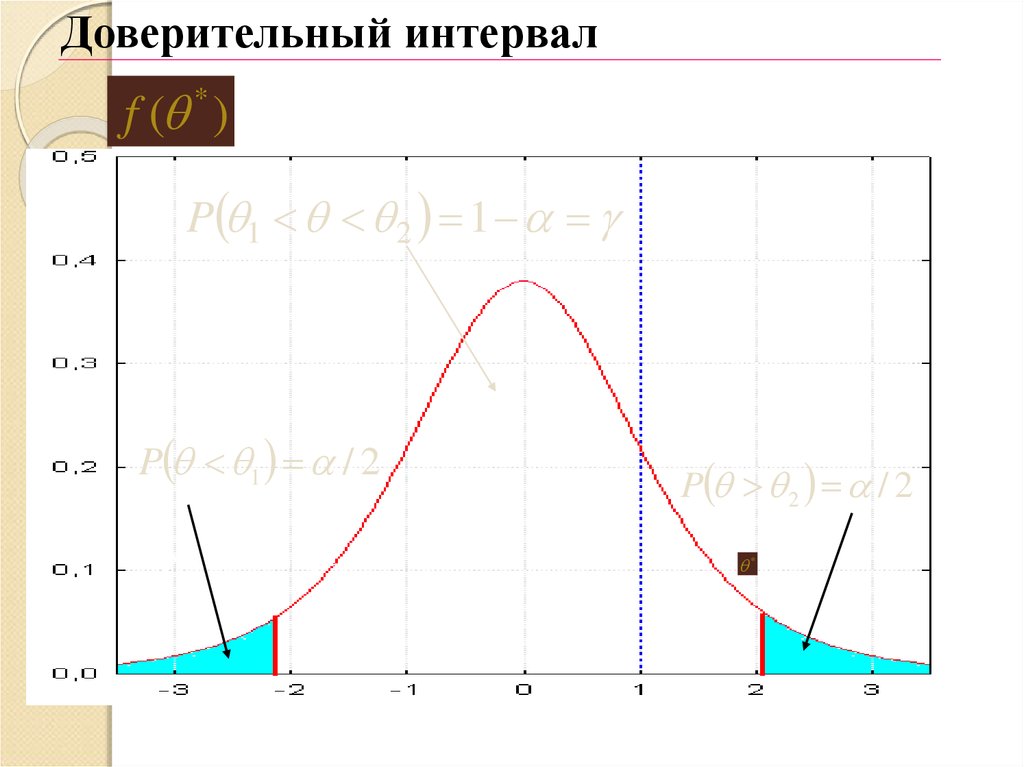
Доверительный интервал
f ( * )
P 1 2 1
P 1 / 2
P 1 2 1
P 2 / 2
*

5. 3 типа задач на доверительные интервалы (ДИ)

1. Построение ДИ для математического
ожидания при известной генеральной
дисперсии (СКО)
2. Построение ДИ для математического
ожидания при неизвестной генеральной
дисперсии (СКО), но известной
исправленной выборочной дисперсии (СКО)
3. Построение ДИ для генеральной
дисперсии (СКО) при известной выборочной
исправленной дисперсии (СКО)

6.

Доверительный интервал для МО нормальной СВ
при известной генеральной дисперсии
1)
2) X ~ N m,
x m
U
~ N 0,1
3)
/ n
4) x u / 2
1
m
n
*
n
xi x
i 1
m x u / 2
n
1
5) Ф u / 2
2
2
n

7.

Точность (предельная погрешность) оценки МО:
1)
2)
u / 2
n

8.

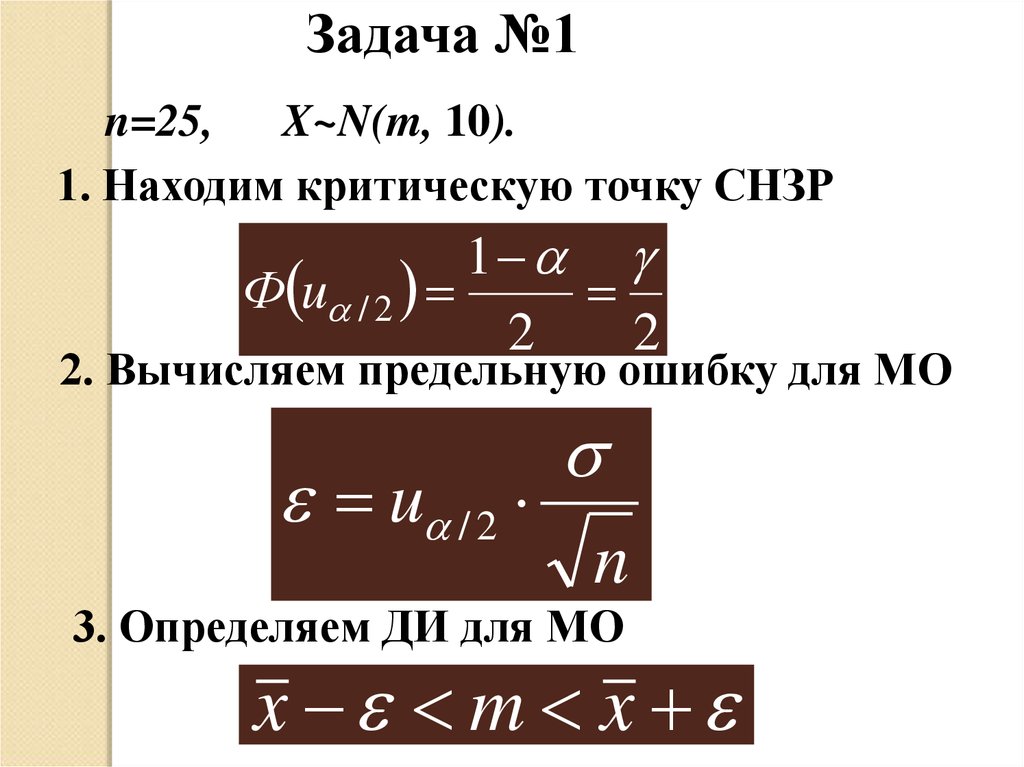
Задача №1
n=25, X~N(m, 10).
1. Находим критическую точку СНЗР
1
Ф u / 2
2
2
2. Вычисляем предельную ошибку для МО
u / 2
n
3. Определяем ДИ для МО
x m x

9.

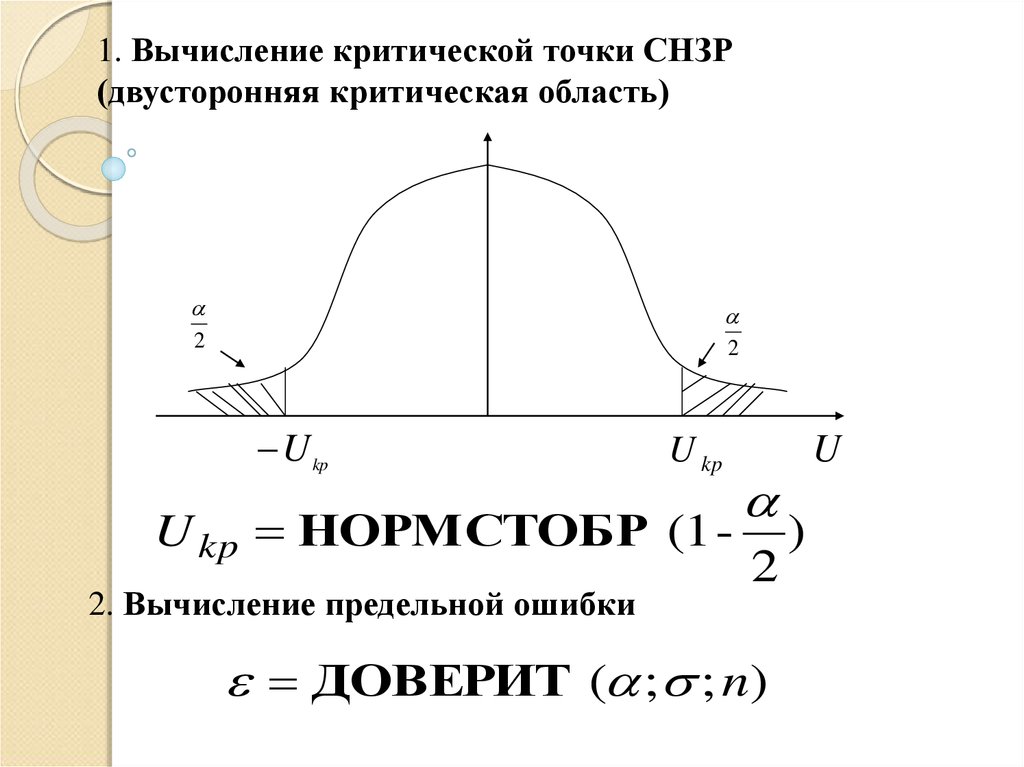
1. Вычисление критической точки СНЗР
(двусторонняя критическая область)
2
2
U kp
U kp
U kp НОРМСТОБР (1 2. Вычисление предельной ошибки
2
ДОВЕРИТ ( ; ; n)
U
)

10.

2. Доверительный интервал для мат. ожидания
нормальной СВ при неизвестной генеральной
дисперсии
1) X ~ N m,
n
n
1
1
2
2
*
m
x
x
,
S
x
x
, S S2
2)
i
i
n 1 i 1
n i 1
3) T x m - Распределение Стьюдента с n-1
степенями свободы
S/ n
s
s
m x t / 2, n 1
4) x t / 2, n 1
n
n

11.

Точность (предельная погрешность) оценки МО:
1)
S
t / 2 ,n 1
n
t ( / 2; n 1) СТЬЮДРАСПОБР( ; n 1)
2)

12.

Доверительный интервал для прогнозируемого
МО нормальной СВ при неизвестной дисперсии
1)
Задана выборка :
x1 , x2 ,..., xn
Построить доверительный интервал для
2)
Доверительный интервал:
1
x t / 2, n 1 S 1 xn 1 x
n
1
t / 2, n 1 S 1
n
xn 1

13.

Задача №2
n=55, X~T(α, n-1).
1. Находим критическую точку РC
t / 2, n 1 СТЬЮДРАСПО БР , n 1
2. Вычисляем предельную ошибку для МО
S
t / 2,n 1
n
3. Определяем ДИ для МО
x m x

14.

Задача №2
4. Вычисление прогноза
1
x t / 2, n 1 S 1 x6 x
n
1
t / 2, n 1 S 1
n

15.

Вычисление критической точки РС
(двусторонняя критическая область)
2
2
t kp
t kp
t
tkp СТЬЮДРАСПОБР( ; n 1) t табл / 2, n 1

16.

3. Доверительный интервал для дисперсии
нормальной СВ при неизвестном МО
1) X ~ N m,
n
2
1
2) m xi x ,
n i 1
*
n
1
2
2
xi x
S
n 1 i 1
2
n
1
S
2
- Распределение хи-квадрат с n-1
3)
2
степенями свободы
4)
2
S 2 n 1
S
n 1
2
2
2
/ 2, n 1
1 / 2, n 1

17.

Задача №2
n=10, x~χ2(α, n-1).
1. Находим критические точки РХК
2 / 2, n 1 ХИ 2ОБР ( / 2, n 1)
1 / 2, n 1 ХИ 2ОБР (1 / 2, n 1)
2
2. Определяем ДИ для дисперсии
S n 1
S n 1
2
2
2
/ 2, n 1
1 / 2, n 1
2
2
3. Определяем ДИ для СКО
S n 1
2
/ 2, n 1
2
S n 1
2
2 1 / 2, n 1

18.

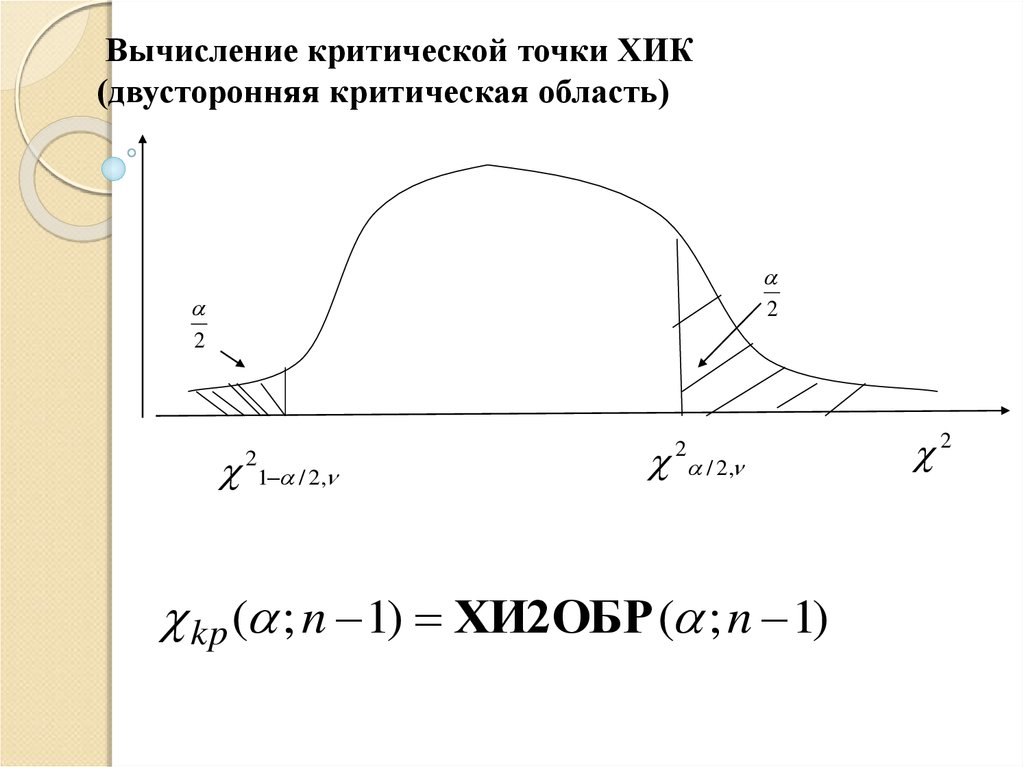
Вычисление критической точки ХИК
(двусторонняя критическая область)
2
2
2
1 / 2,
2
/ 2 ,
kp ( ; n 1) ХИ2ОБР ( ; n 1)
2