Термодинамика и молекулярная физика. Лекция 6

1.

ТЕРМОДИНАМИКА И
МОЛЕКУЛЯРНАЯ ФИЗИКА
Лекция 6

2.

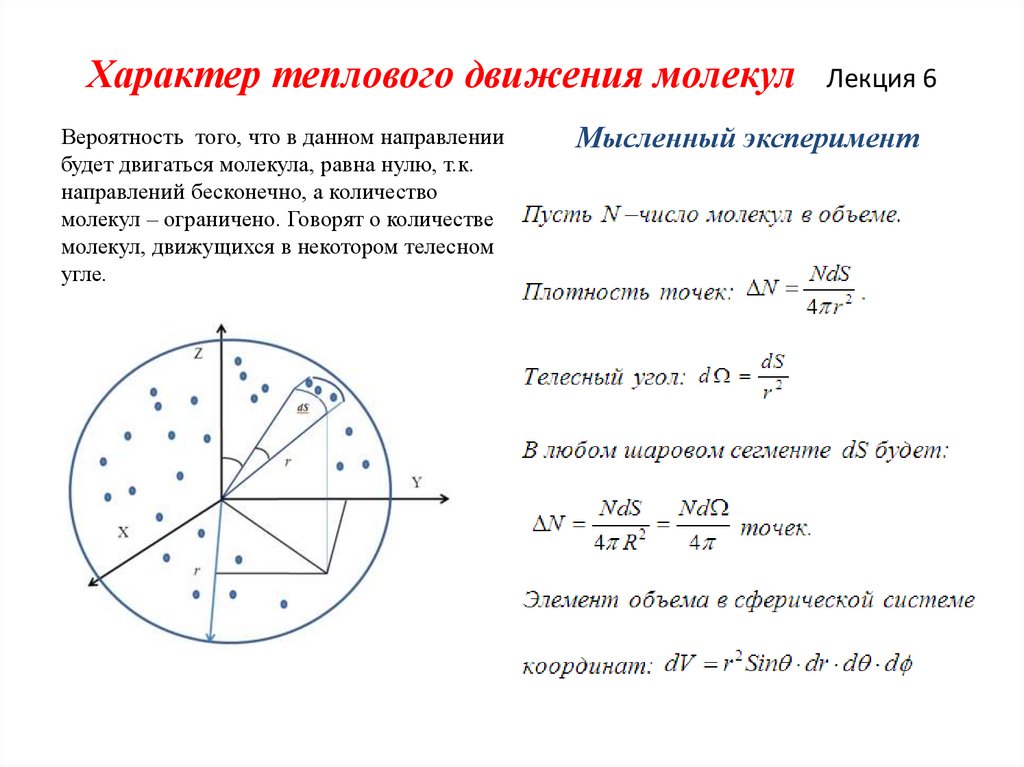
Характер теплового движения молекул
Вероятность того, что в данном направлении
будет двигаться молекула, равна нулю, т.к.
направлений бесконечно, а количество
молекул – ограничено. Говорят о количестве
молекул, движущихся в некотором телесном
угле.
Лекция 6
Мысленный эксперимент

3.

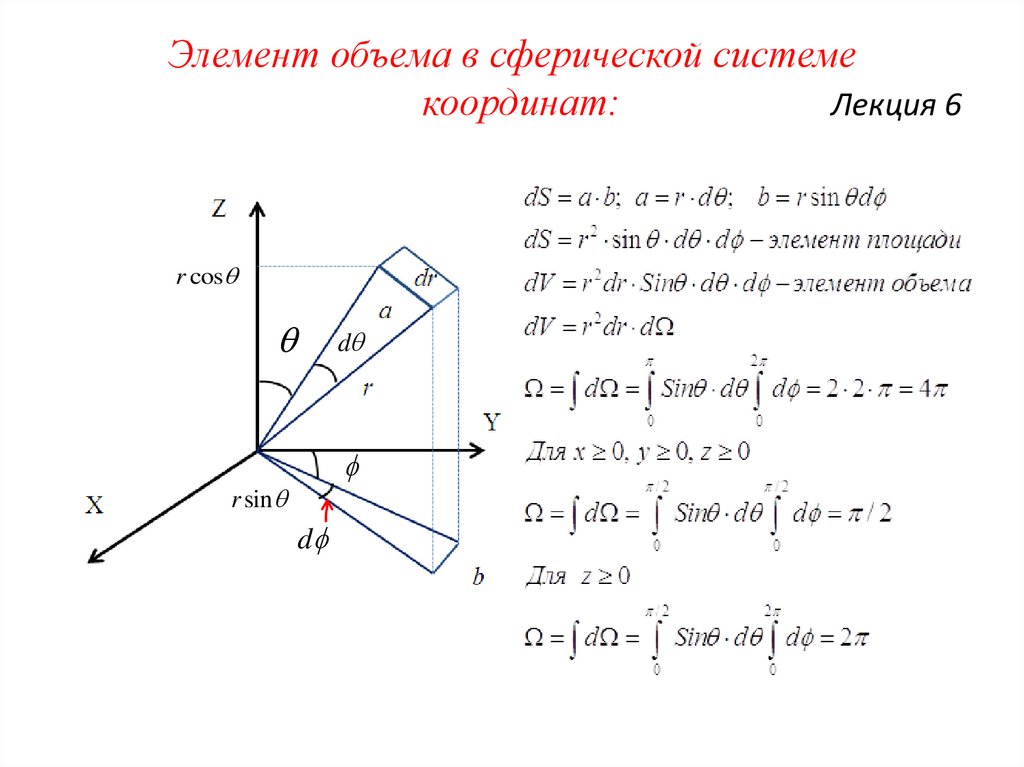
Элемент объема в сферической системе
координат:
Лекция 6
r cos
d
r sin
d

4.

Число ударов молекул о стенку
Лекция 6
Считаем количество ударов молекул об элемент поверхности стенки
сосуда dS за время dt.
1. Выделяем N – молекул со скоростями: от v до v+dv. Обозначим их
число: dNv.
2. Выделяем из dNv молекулы внутри d . Обозначим их число: dN v , , .
3. За время dt из этих молекул долетят только те, которые находятся в
косом цилиндре с основанием dS и высотой dh v Cos dt .
Доля таких молекул:
Число таких молекул:
, или

5.

Число ударов молекул о стенку Лекция 6
Полное число молекул за dt ударившихся в dS будет:
ds ,dt
dt dS
4V
vmax
0
dt dS N
vNf (v)d
4V
vmax
0
vf (v)d
dt dS N
v
4V
dt dS n
n – плотность числа частиц
v
4
Число молекул, ударившихся о единичную площадку за единицу времени:
ds ,dt

6.

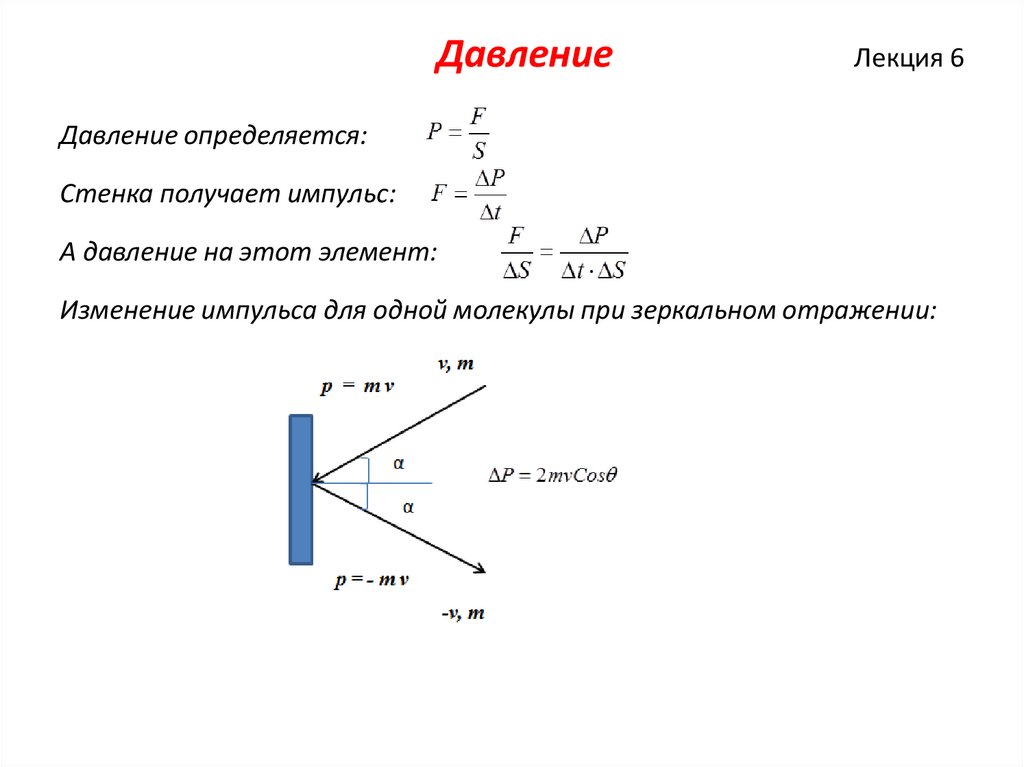
Давление
Лекция 6
Давление определяется:
Стенка получает импульс:
А давление на этот элемент:
Изменение импульса для одной молекулы при зеркальном отражении:

7.

Давление
Лекция 6
Количество молекул, падающих на S и имеющих скорости
от v до v+dv равно:
Тогда суммарный импульс dK v , , будет:
Интегрируем по углам:

8.

Давление
Лекция 6
Тогда:
Получим выражение для давления:
Все молекулы одинаковые по массе:
- средняя кинетическая энергия поступательного движения.

9.

Пример
Есть 4 молекулы со скоростями: vi = 1,2,3,4.
Найти:

10.

Средняя энергия молекул
Мы получили: P
Лекция 6
2n
Eкин , P nkT
3
Откуда:
Основное уравнение молекулярно-кинетической теории
Eкин
T
- усредненный микропараметр
- макропараметр

11.

Средняя энергия молекул
Получаем скорость:
mv 2
3kT
2
2
v2
3kT
m
Вследствие эквивалентности направлений:
Поэтому,
Т.е.,
Лекция 6

12.

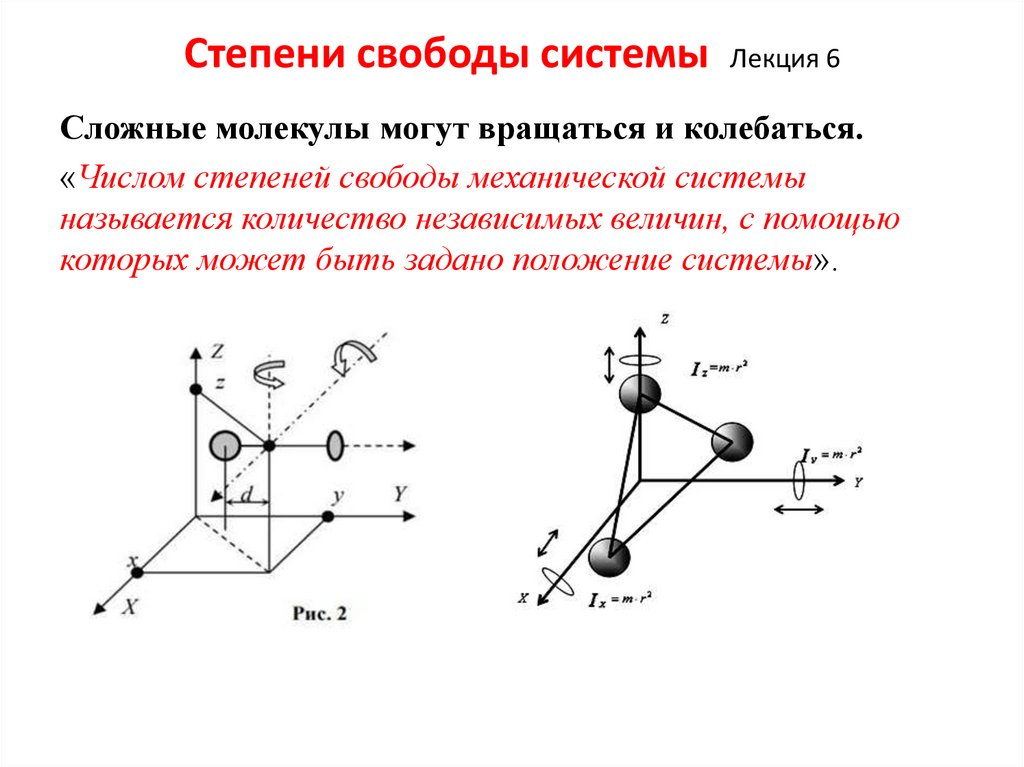
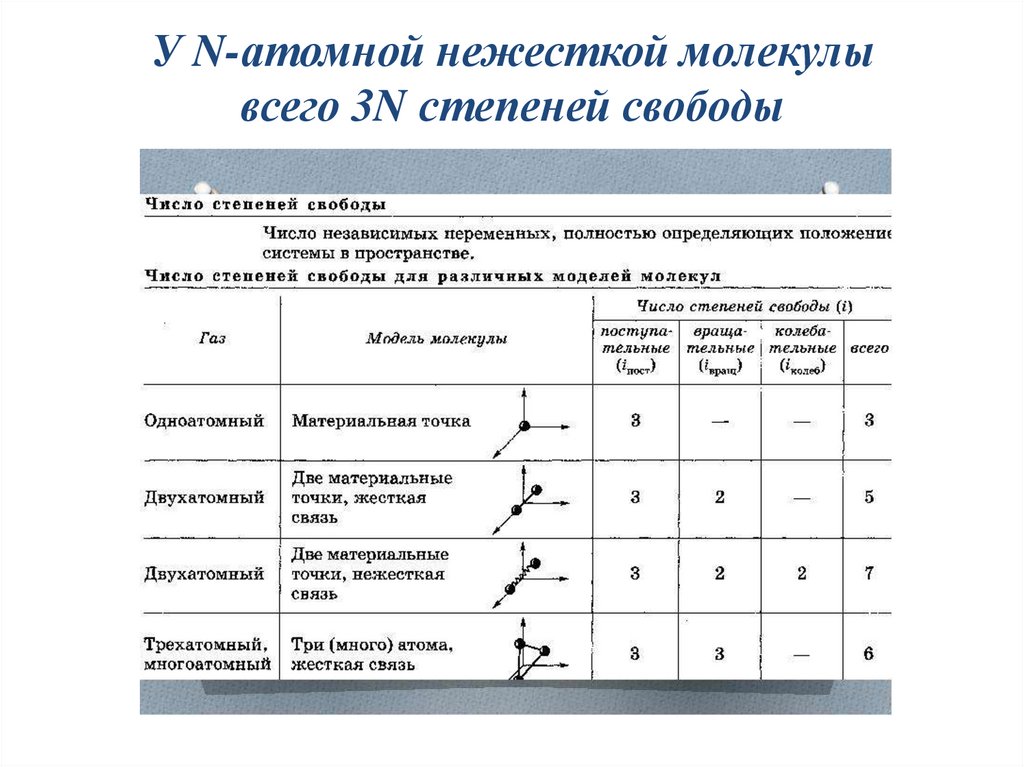
Степени свободы системы
Лекция 6
Сложные молекулы могут вращаться и колебаться.
«Числом степеней свободы механической системы
называется количество независимых величин, с помощью
которых может быть задано положение системы».

13.

Закон равнораспределения энергии по степеням
свободы
Лекция 6
На каждую степень свободы приходится kT/2 энергии.
Т.е. средняя энергия молекулы равна:
Где
- полное число степеней свободы
Почему у колебательной степени энергия в 2 раза больше?

14.

Идеальный газ
Внутренняя энергия 1 моля идеального газа равна
UM NA E
i
i
kT RT
2
2
С другой стороны: U M CV T
UM NA E NA
Отсюда:
Лекция 6

15.

У N-атомной нежесткой молекулы
всего 3N степеней свободы

16.

17.

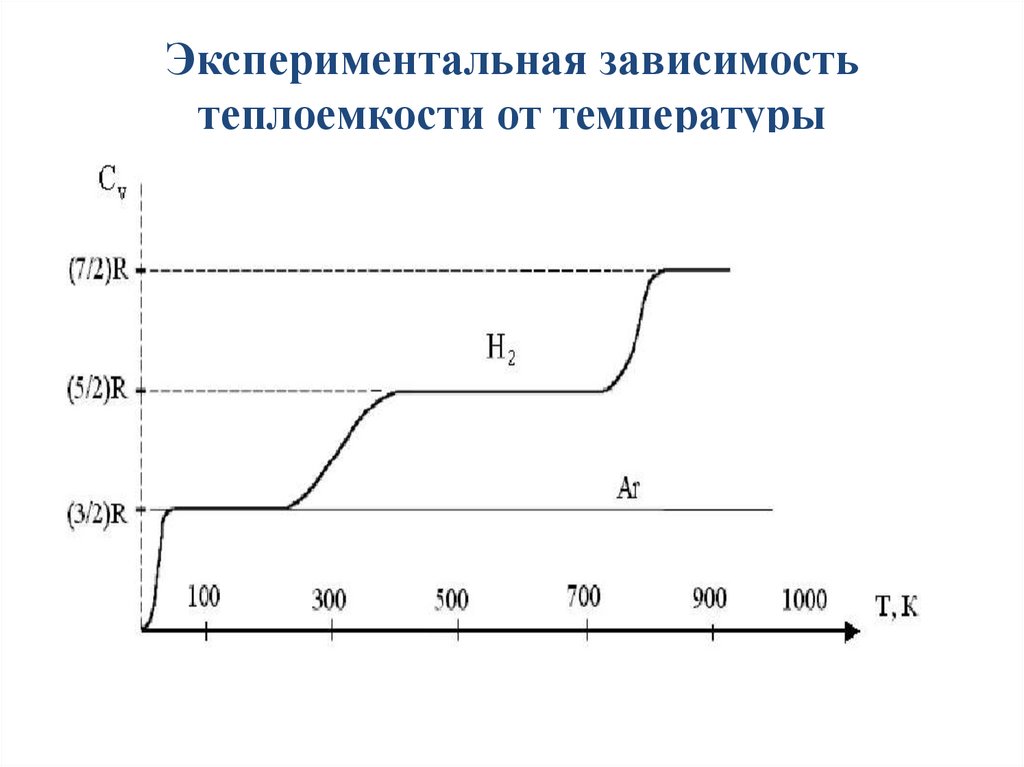
Экспериментальная зависимость
теплоемкости от температуры