Статистическая радиотехника. Импульсные случайные процессы. Лекция 4

1.

Курс лекций по
дисциплине
СТАТИСТИЧЕСКАЯ
РАДИОТЕХНИКА
Лекция 4
Лектор - Куроедов
Сергей Константинович

2. ПЛАН ЛЕКЦИИ 1-4

1. Импульсные случайные процессы,
квазидетерминированные импульсные
случайные процессы
2. Перекрывающиеся и
неперекрывающиеся случайные
импульсы, условия отсутствия и
наличия перекрытия
3. Энергетический спектр реализации
стационарной случайной
последовательности
неперекрывающихся импульсов

3. ПЛАН ЛЕКЦИИ 4

4.Спектр мощности стационарной
случайной последовательности
неперекрывающихся импульсов
5. Спектр мощности периодически
повторяющихся импульсов заданной
формы со случайными амплитудами
6. Спектр мощности периодически
повторяющихся импульсов заданной
формы с некоррелированными
случайными амплитудами
7.Спектр мощности пуассоновской по

4. ПЛАН ЛЕКЦИИ 4

8. Спектр мощности квазипериодического
импульсного случайного процесса с
независимыми стационарными
амплитудами и смещениями импульсов
9. Спектр мощности случайной
последовательности импульсов с
постоянной амплитудой и
стационарными случайными
смещениями во времени
10. Спектр мощности независимых
перекрывающихся импульсов
11.Спектр мощности пуассоновской
последовательности независимых
перекрывающихся импульсов

5. ПЛАН ЛЕКЦИИ 4

12. Спектр мощности
квазипериодического импульсного
случайного процесса с независимыми
стационарными амплитудами и
смещениями импульсов
13. Спектр мощности случайной
последовательности импульсов с
постоянной амплитудой и
стационарными случайными
смещениями во времени
14. Спектр мощности независимых
перекрывающихся импульсов
15.Спектр мощности пуассоновской
последовательности независимых
перекрывающихся импульсов

6.

ИМПУЛЬСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Импульсным называется случайный
процесс в виде импульсной
последовательности с априорно
неизвестными характеристиками.
Априорно неизвестными могут быть
форма каждого случайного импульса
последовательности, его время
появления, основные, дополнительные и
производные параметры.
Импульсные случайные процессы, часть
характеристик которых являются
априорно известными, называются
квазидетерминированными.

7.

ИМПУЛЬСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Случайные финитные импульсы могут
быть неперекрывающимися и
перекрывающимися. Под перекрытием
понимается частичное наложение
импульсов друг на друга.
Условие отсутствия перекрытия
импульсов определяется неравенством
ti 1 i 1 ti
ti-1 и ti – эпохи (моменты появления) (i-1) го и i – го импульсов, τi-1 - длительность
(i-1)-го импульса

8.

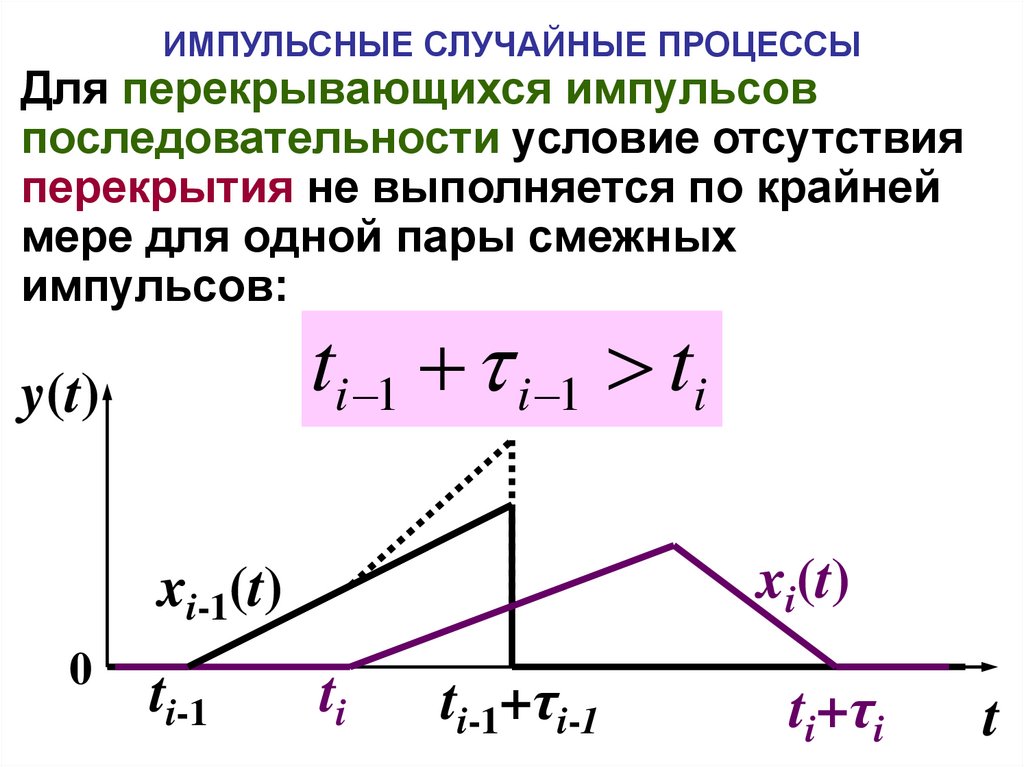
ИМПУЛЬСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Для перекрывающихся импульсов
последовательности условие отсутствия
перекрытия не выполняется по крайней
мере для одной пары смежных
импульсов:
ti 1 i 1 ti
y(t)
xi(t)
xi-1(t)
0
ti-1
ti
ti-1+τi-1
ti+τi
t

9.

СТАЦИОНАРНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
НЕПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
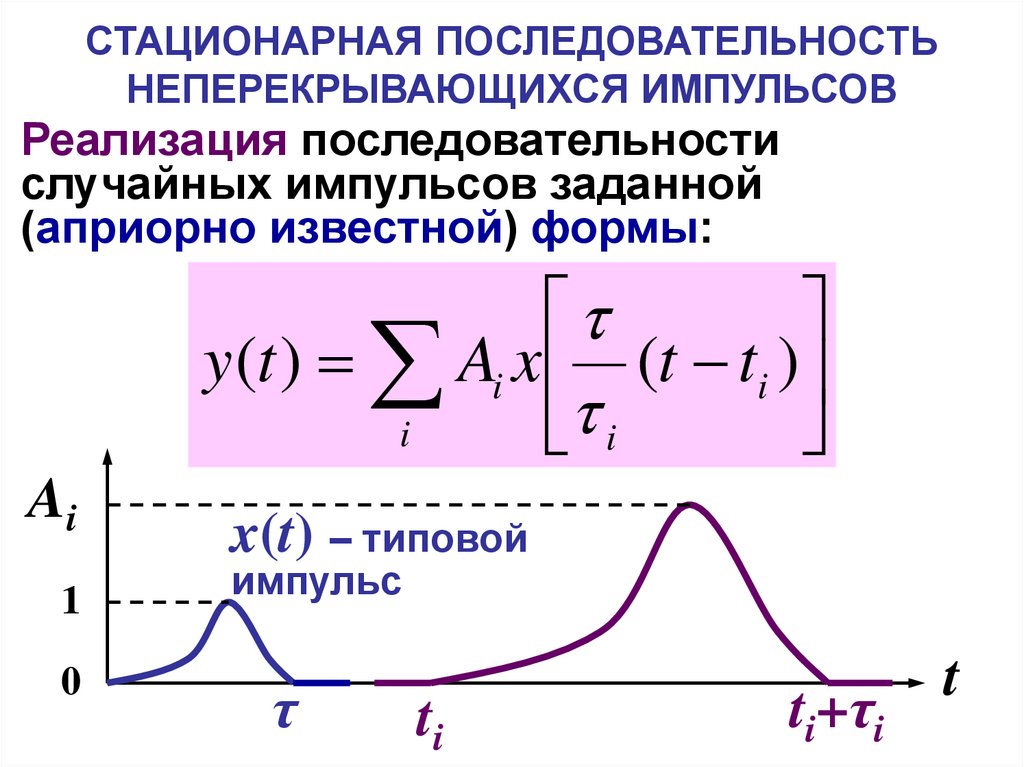
Реализация последовательности
случайных импульсов заданной
(априорно известной) формы:
y (t ) Ai x (t ti )
i
i
Ai
1
0
x(t) – типовой
импульс
τ
ti
ti+τi
t

10.

СТАЦИОНАРНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
НЕПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Спектральные плотности типового
импульса и его смещенной масштабной
копии:
X ( )
x
(
t
)
e
j t
dt
i i
Ai x (t ti ) Ai X
e
i
j ti
i

11.

СТАЦИОНАРНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
НЕПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Спектральная плотность реализации
импульсной последовательности:
i i
Y ( ) Ai X
e
i N
N
j ti
Энергетический спектр реализации:
Y ( ) Y ( )Y ( )
2
i

12.

СТАЦИОНАРНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
НЕПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Энергетический спектр реализации:
i k i
Y ( ) Ai Ak 2 X
i N k N
2
k
X
N
e
N
ti t k
j
i k
n i k, i n k

13.

СТАЦИОНАРНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
НЕПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Энергетический спектр реализации:
n k k n k
Y ( ) An k Ak
X
2
n 2 N k N
2
k
X
2N
e
N
tn k tk
j
n k k

14.

СТАЦИОНАРНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
НЕПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Спектр мощности последовательности:
1
2
W ( ) lim YT ( )
T T
T – случайная длительность реализации,
включающей (2N+1)-импульсов
θi = ti+1- ti – длительность интервала
времени между эпохами двух соседних
импульсов
T (2 N 1) T , lim T
T

15.

СТАЦИОНАРНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
НЕПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Спектр мощности последовательности:
W ( )
1
n k
X
n
n k k
An k Ak
2
k
X
e
tn k t k
j
n k k

16.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
y(t)
ζ(t)
A0
-θ
0
A-1
τ
θ 2θ
t
A1
θi = θ – постоянный период повторения
импульсов с постоянной длительностью
τi = τ

17.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
Ai – случайные амплитуды импульсов,
которые определяются выборками
стационарного случайного процесса ζ(t):
Ai = ζ(i θ)
k k n , tn k tk n ,
An k Ak K (n ) R (n ) m
2
где Kζ(τ) – функция ковариации, Rζ(τ)
функция корреляции, mζ - математическое
ожидание случайного процесса ζ(t)

18.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
Подставляем в формулу для W(ω):
X 2 j n
j n
W ( )
m e
e R (n )
n
n
2
Учитываем разложение периодической
последовательности дельта-функций в
комплексный ряд Фурье:
2
2 n
j n
e
n
n

19.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
Окончательно получаем:
2 m X
2
W ( )
X
2
e
n
2
j n
2
2 n
n
R (n )

20.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
Для того, чтобы перейти в полученном
выражении от функции корреляции Rζ(τ)
к спектру мощности Wζ(ω) случайного
процесса ζ(t), используем теорему
Винера-Хинчина:
1
R ( )
2
W
(
)
e
j
d

21.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
Второе слагаемое в формуле для W (ω)
запишется так:
e
j n
R (n )
n
1
2
e
)
(
W
n
j ( ) n
d

22.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
Сумму комплексных экспонент в
подынтегральном выражении заменим
периодической последовательностью
масштабных копий дельта-функций:
e
j n
n
2 n
R (n ) W ( )
d
n
1
Используя фильтрующее свойство
дельта-функций, получаем:
e
n
j n
2 n
R (n ) W
n
1

23.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
После подстановки в формулу для W (ω)
полученного выражения для второго
слагаемого окончательно получаем:
X 2
2 n
W ( )
m
2
n
2
2 n
W
n

24.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ АМПЛИТУДАМИ
Из полученного выражения следует, что
спектр мощности W (ω) периодически
повторяющихся импульсов заданной
формы со случайными амплитудами в
общем случае состоит из непрерывной и
дискретной частей. Дискретные
спектральные линии на частотах ω = nω0,
кратных частоте ω0 = 2πθ-1 следования
импульсов, обусловлены стробированием
mζ случайного процесса ζ(t). При mζ = 0
спектр мощности не содержит дискретной
части и является сплошным.

25.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ
НЕКОРРЕЛИРОВАННЫМИ АМПЛИТУДАМИ
Если период θ следования импульсов
значительно больше времени корреляции
τk процесса ζ(t), то случайные амплитуды
Ai импульсов можно считать
некоррелированными:
R (n ) 0, n 0, R (0)
2
В этом случае во втором слагаемом
выражения для W(ω) отличным от нуля
будет только одно слагаемое при n = 0

26.

ПЕРИОДИЧЕСКИ ПОВТОРЯЮЩИЕСЯ ИМПУЛЬСЫ
ЗАДАННОЙ ФОРМЫ СО СЛУЧАЙНЫМИ
НЕКОРРЕЛИРОВАННЫМИ АМПЛИТУДАМИ
2
2
W ( )
2 m X
X
2
2
2 n
n
2
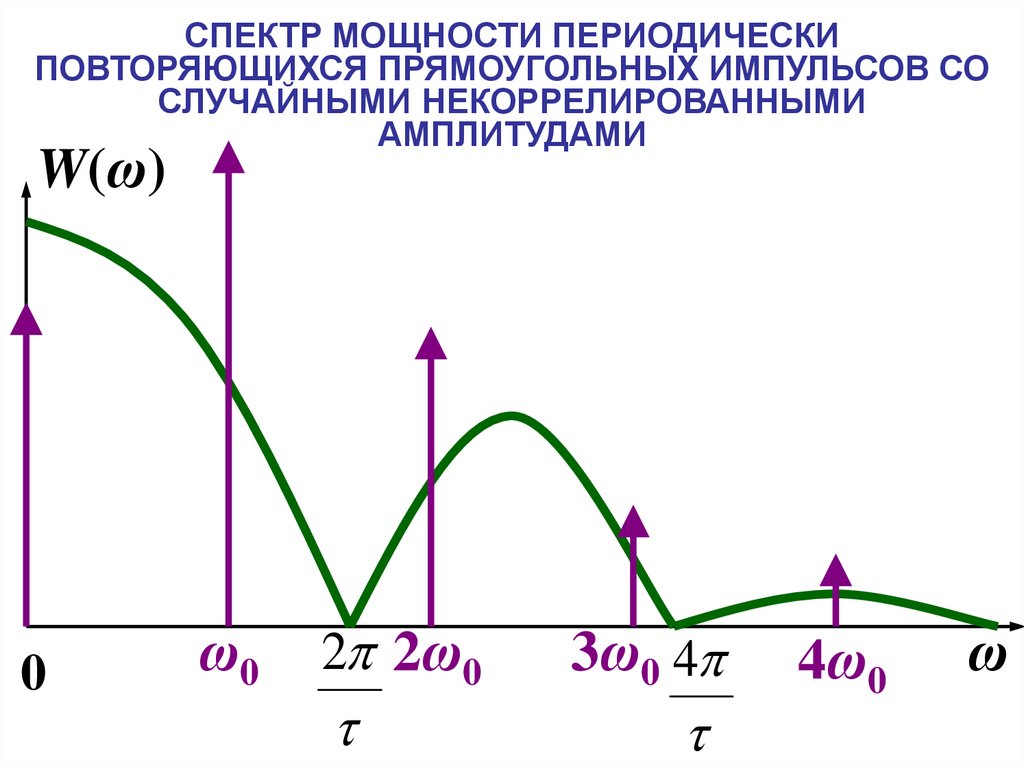
Как следует из полученного выражения,
при некоррелированных Ai непрерывная
часть W(ω) является масштабной копией
энергетического спектра типового
импульса x(t)

27.

СПЕКТР МОЩНОСТИ ПЕРИОДИЧЕСКИ
ПОВТОРЯЮЩИХСЯ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ СО
СЛУЧАЙНЫМИ НЕКОРРЕЛИРОВАННЫМИ
АМПЛИТУДАМИ
W(ω)
0
ω0
2 2ω0
3ω0 4
4ω0
ω

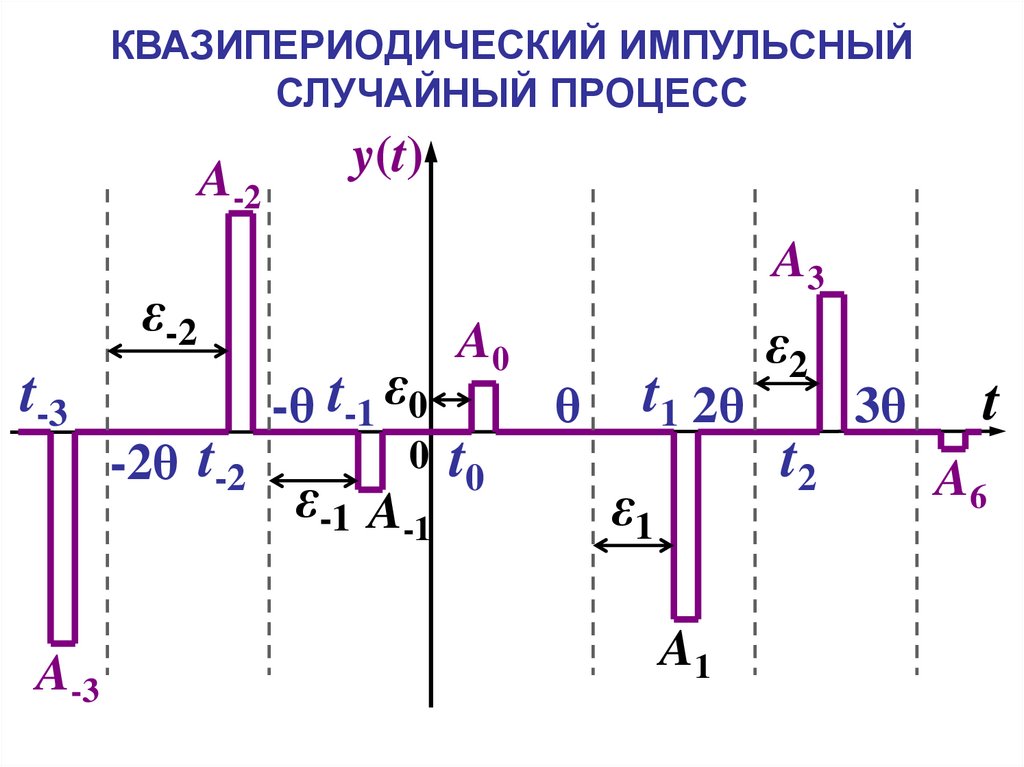
28.

КВАЗИПЕРИОДИЧЕСКИЙ ИМПУЛЬСНЫЙ
СЛУЧАЙНЫЙ ПРОЦЕСС
A-2
ε-2
t-3
-2θ t-2
A-3
y(t)
A3
ε
t
-θ -1 0
0
ε-1 A-1
A0
t0
θ
t1 2θ
ε2
3θ
t2
ε1
A1
t
A6

29.

КВАЗИПЕРИОДИЧЕСКИЙ ИМПУЛЬСНЫЙ СЛУЧАЙНЫЙ
ПРОЦЕСС С НЕЗАВИСИМЫМИ СТАЦИОНАРНЫМИ
СЛУЧАЙНЫМИ АМПЛИТУДАМИ И СМЕЩЕНИЯМИ
ИМПУЛЬСОВ
k k n , tk n k ,
tn k t k n k n k , An k Ak A
( ) e
j ( t k 1 t k )
e
j
2
( ) , ( ) e
2
Θ(ω) – характеристическая функция
квазипериодов - длительностей (tk+1- tk)
j
интервалов между соседними
импульсами, Θε(ω) – характеристическая
функция смещений εk

30.

КВАЗИПЕРИОДИЧЕСКИЙ ИМПУЛЬСНЫЙ СЛУЧАЙНЫЙ
ПРОЦЕСС С НЕЗАВИСИМЫМИ СТАЦИОНАРНЫМИ
СЛУЧАЙНЫМИ АМПЛИТУДАМИ И СМЕЩЕНИЯМИ
ИМПУЛЬСОВ
После подстановки в общее выражение
для W(ω) выделим слагаемые с n = 0, n ≥
1, n ≤ -1 и используем формулу
разложения периодической
последовательности дельта-импульсов в
комплексный ряд Фурье
2
2 n
j n
e
n
n

31.

СПЕКТР МОЩНОСТИ СЛУЧАЙНОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ ИМПУЛЬСОВ С
НЕЗАВИСИМЫМИ СТАЦИОНАРНЫМИ АМПЛИТУДАМИ И
СМЕЩЕНИЯМИ
W ( )
A
2
X
2
2
A
2
A ( )
2
2
m
( )
m
2
2

32.

СПЕКТР МОЩНОСТИ КВАЗИПЕРИОДИЧЕСКОГО
ИМПУЛЬСНОГО СЛУЧАЙНОГО ПРОЦЕССА
Из полученного выражения следует, что
спектр мощности W (ω)
квазипериодического импульсного
случайного процесса в общем случае
состоит из непрерывной и дискретной
частей. При ‹A› = 0 спектр мощности не
содержит дискретной части и является
сплошным.
Если εi = const , то выражение для W (ω)
приводится к выражению для спектра
мощности периодически повторяющихся
импульсов со случайными амплитудами

33.

СПЕКТР МОЩНОСТИ СЛУЧАЙНОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ ИМПУЛЬСОВ С
ПОСТОЯННЫМИ АМПЛИТУДАМИ
Если амплитуды импульсов Ai = A = const ,
то выражение для W (ω) приводится к
следующему виду:
W ( )
A
2
X 1 ( )
2
2
2
2 m
( )
m
1
2

34.

СЛУЧАЙНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
НЕЗАВИСИМЫХ ПЕРЕКРЫВАЮЩИХСЯ
ИМПУЛЬСОВ
Реализация случайной
последовательности перекрывающихся
импульсов на интервале (0,T) :
y (t ) Ai x (t ti )
i 0
i
N (T )
N (T) – число импульсов реализации,
T – длительность реализации

35.

СПЕКТР МОЩНОСТИ СЛУЧАЙНОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
N (T ) N (T )
i k
i k
2
T
i 0 i 0
1
W ( ) lim
T
AA
i k
X
X
e
ti t k
j
i k
Число импульсов N (T) является
случайной величиной, поэтому
статистическое усреднение должно
распространяться и на N (T)

36.

СПЕКТР МОЩНОСТИ СЛУЧАЙНОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
1
W ( ) lim
T T
N (T ) N (T )
i 0 k 0
i k
X
X
e
i k
Ai Ak 2
ti t k
j
i k
Выделим из двойной суммы, содержащей
‹N(T)›2 слагаемых, ‹N(T)› слагаемых с
одинаковыми индексами i = k

37.

СПЕКТР МОЩНОСТИ СЛУЧАЙНОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
2
N(T)
2
1
i
2 τi
W ( ) lim Ai 2 X
T T
τ
i 0
N(T) N(T)
i 0 k 0
i k k i
τ i τ k i k
Ai Ak 2 X
X
τ
e
ti t k
j
i k
Если случайные величины Ai , τi и ti
стационарны, то их средние значения не
зависят от индекса i

38.

СПЕКТР МОЩНОСТИ СЛУЧАЙНОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Если Ai , τi и ti независимы, то
N (T ) 2 2
2
W ( ) lim
A x X x
T
T
j
N (T ) N (T )
i
lim
A x X x e
T
T
2
A x X x e
ti
j
tk
k

39.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
τx – безразмерная длительность
импульса, нормированная длительностью
типового импульса
Если случайное число N(T) импульсов на
интервале времени (0, T) распределено по
закону Пуассона, то существуют пределы
2
N (T )
N (T ) N (T )
2
lim
, lim
2
T
T
T
T

40.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
λ – среднее число импульсов в единицу
времени
Подставляем полученные значения
пределов в выражение для W (ω) :
W ( ) A τ X x
2 2
x
Aτ x X x
2
2
j
2
xi
lim T e
T
ti

41.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Примем, что эпохи ti равномерно
распределены на интервале (0, T), тогда
их плотность вероятности
0, ti (0, T );
p (ti ) 1
,
t
(
0
,
T
).
i
T
Используем p(ti) для того, чтобы
вычислить предел в правой части
выражения для W (ω), считая, что τi =
τ

42.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
e
j t i
2
1
2
T
T
e
2
j ti
dti
0
T
2 sin
1
2
lim
T T
2
T
2 sin
2
T
0, 0;
, 0.
2

43.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Учитывая, что
T
2 sin
1
2
T
2
d 2
получаем:
lim T e
T
j ti
2
2 ( )

44.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Введем величину, характеризующую
плотность импульсной
последовательности или число
импульсов, приходящихся в среднем на
длительность одного импульса:
Чем больше γ, тем больше степень
перекрытия импульсов и наоборот

45.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
W ( )
2
A X
2
A X 0 2 ( )
2
2
2

46.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Из полученного выражения следует, что
спектр мощности W (ω) пуассоновской
последовательности независимых
перекрывающихся импульсов
описывается двумя слагаемыми. Первое
слагаемое определяется математическим
ожиданием энергетического спектра
случайного импульса, взвешенным
параметром λ .

47.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Второе слагаемое представляет собой
масштабную копию дельта-функции
частоты, взвешенную квадратом
произведения параметра λ и средней
площади случайного импульса. Средняя
площадь случайного импульса
определяется математическим ожиданием
значения его спектральной плотности в
нуле, которое, в свою очередь, при
отсутствии перекрытия определяет
квадрат среднего значения импульсной
последовательности

48.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
Влияние перекрытия случайных
импульсов на квадрат их среднего
значения можно рассмотреть на
следующем примере.
При γ = 1 два прямоугольных импульса с
одинаковыми длительностями и
амплитудами в среднестатистическом
смысле не перекрываются и между ними
отсутствует пауза, поэтому квадрат их
среднего значения определяется
квадратом амплитуды

49.

СПЕКТР МОЩНОСТИ ПУАССОНОВСКОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
ПЕРЕКРЫВАЮЩИХСЯ ИМПУЛЬСОВ
При γ = 2 в среднем наблюдается полное
перекрытие двух импульсов, амплитуда
суммы импульсов увеличивается в два
раза, а квадрат их среднего значения – в
четыре раза. В четыре раза
увеличивается площадь дельта-функции
частоты, которая описывает спектр
мощности импульсной
последовательности при нулевом
значении частоты.