Similar presentations:
Активное, ёмкостное и индуктивное сопротивления
1.
Активное, ёмкостное ииндуктивное
сопротивления
Изучите тему. В тетради выполните конспект,
подготовьтесь к практической работе по решению задач
(разберите примеры решения задач)
2.
Активное сопротивлениеАктивное сопротивление –R: обычное
электрическое сопротивление проводника, в
котором происходит превращение
электрической энергии во внутреннюю.
l
R
s
-активное сопротивление
проводника
l- длина проводника, s-площадь поперечного
сечения, ρ-удельное сопротивление.
3.
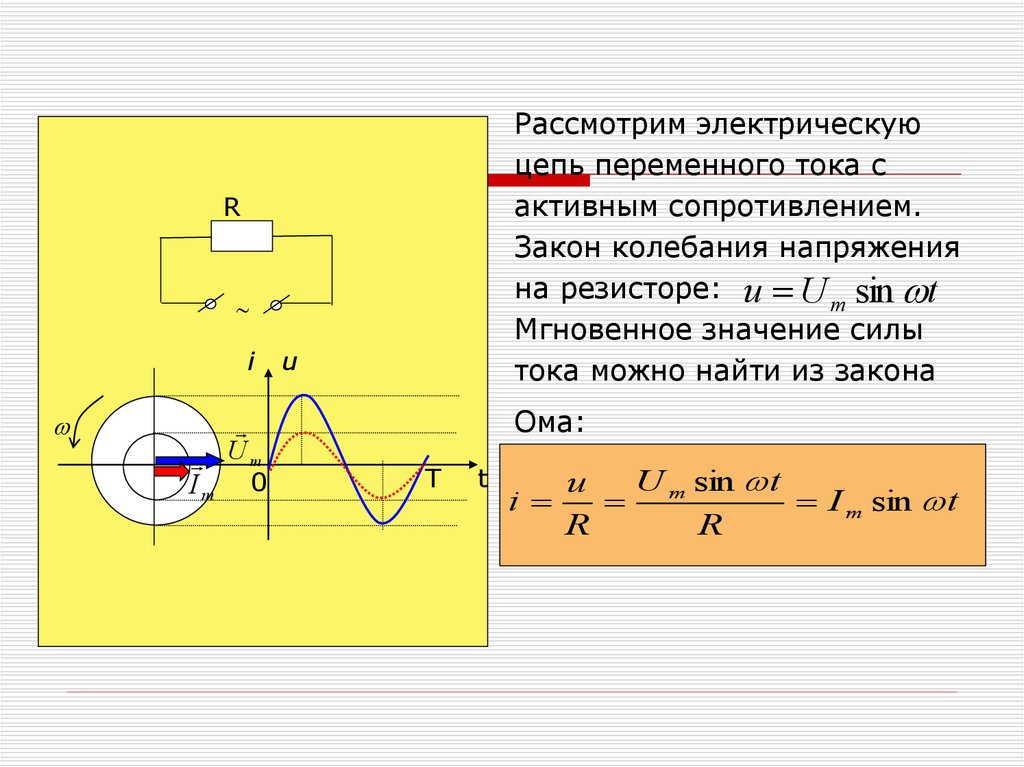
Рассмотрим электрическуюцепь переменного тока с
активным сопротивлением.
Закон колебания напряжения
на резисторе: u U m sin t
Мгновенное значение силы
тока можно найти из закона
R
i
Um
Im 0
u
Ома:
T
t
i
U sin t
u
m
I m sin t
R
R
4.
ВыводыКолебания силы тока и напряжения на
активном сопротивлении совпадают по
фазе.
Амплитудные и действующие значения
U .
связаны формулой:
Um и
I
Im
R
R
При низких частотах активное
сопротивление не зависит от частоты.
На активном сопротивлении происходят
безвозвратные превращения
электрической энергии во внутреннюю.
5.
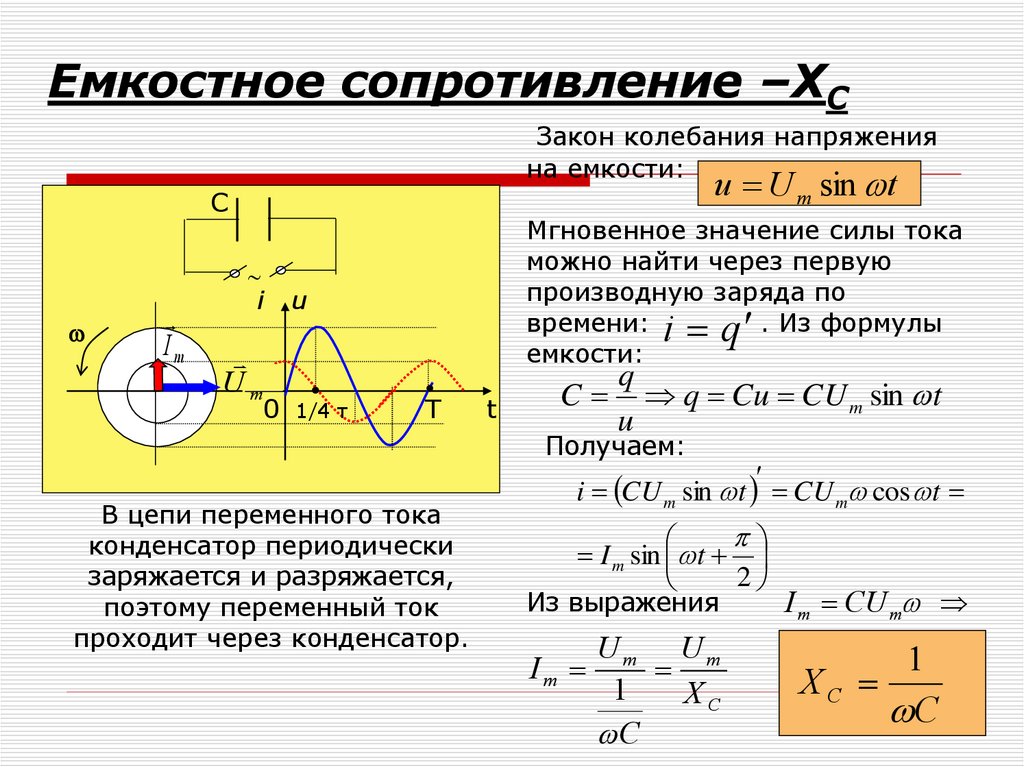
Емкостное сопротивление –XCЗакон колебания напряжения
на емкости:
u U m sin t
C
Im
i
Um
0
Мгновенное значение силы тока
можно найти через первую
производную заряда по
времени: i q . Из формулы
емкости:
u
1/4 т
T
t
q
C q Cu CU m sin t
u
Получаем:
В цепи переменного тока
конденсатор периодически
заряжается и разряжается,
поэтому переменный ток
проходит через конденсатор.
i CU m sin t CU m cos t
I m sin t
2
Из выражения
I m CU m
Um Um
Im
1
XC
C
1
XC
C
6.
ВыводыКолебания силы тока опережают колебания
напряжения на емкости по фазе /2 или на ¼ T.
Емкостное сопротивление обратно пропорционально
емкости и частоте переменного тока.
1
XC
C
Амплитудные и действующие значения связаны
U
формулой: I U m и
.
I
m
XC
XC
Потребляемая энергия за период равна нулю:
половину периода конденсатор запасает энергию,
вторую половину периода отдает энергию в цепь.
7.
Индуктивное сопротивление- XLL
ω
Um
i
Im 0
X L L
u
¼T
T
t
- индуктивное
сопротивление
В цепи переменного
тока в катушке
возникает ЭДС
самоиндукции, которая
противодействует
изменениям силы тока.
Это приводит к
появлению
дополнительного
сопротивления –
индуктивного.
8.
Рассмотрим электрическую цепьпеременного тока с индуктивностью L.
Закон колебания силы тока в цепи:
i I m sin t
u e iR
Из закона Ома для участка цепи с ЭДС получаем:
Рассмотрим идеальную катушку, для которой R=0.
Из закона э-м индукции : L I -среднее значение ЭДС
is
t самоиндукции
, что мгновенное значение ЭДС самоиндукции пропорционально
первой производной силы тока: e Li Получаем:
u e 0 u e Li
u L I m sin t I m L cos t U m sin t
2
U
U
Из выражения U I L I m m
m
m
m
XL
L X L
L
9.
ВыводыКолебания силы тока отстают от колебаний
напряжения по фазе на или на ¼ периода.
2
Индуктивное сопротивление пропорционально
круговой частоте ω и индуктивности L.
Амплитудные и действующие значения связаны
формулами:
Um и I U .
Im
XL
XL
Потребляемая энергия за период равна нулю:
половину периода энергия накапливается в
магнитном поле катушки, вторую половину периода
катушка отдает энергию в цепь.
10.
11.
Характеристики сопротивленийв цепи переменного тока
12.
13.
Задача 1. В цепи переменного тока с частотой50 Гц при напряжении 220 В возникает сила тока
4 А. Известно, что в эту цепь включена катушка с
ничтожно малым активным сопротивлением.
Какова индуктивность катушки?
ДАНО: РЕШЕНИЕ
Индуктивное сопротивление определяется по
формуле
Циклическую частоту можно рассчитать по
выражению
Запишем закон Ома для участка цепи
Приравняем две последних формулы для
расчёта индуктивного сопротивления и
выразим индуктивность катушки
14.
Ответ: 175 мГн.15.
Задача 2. . При увеличении частоты от 50 Гц до 60 Гц,ёмкостное сопротивление конденсатора с постоянной
ёмкостью уменьшилось на 10 Ом. Найдите электроёмкость
конденсатора.
РЕШЕНИЕ
Ёмкостное сопротивление определяется по формуле
Циклическую частоту можно определить по
выражению
Тогда ёмкостное сопротивление
Применим данную формулу для двух значений
частоты
Изменение ёмкостного сопротивления конденсатора
определяется по формуле
16.
Тогда электроёмкость конденсатораОтвет: 53 мкФ.
















 physics
physics








