Similar presentations:
Проекции с числовыми отметками. Лекция 14
1.
Лекция 14ПРОЕКЦИИ
С ЧИСЛОВЫМИ
ОТМЕТКАМИ
Красовская Н.И.
2.
.Метод проекций с числовыми
отметками
используется в инженерной графике
при изображении предметов, размеры
которых в плане значительно больше
их вертикальных размеров, т.е. в тех
случаях, когда не представляется
возможным
показать в одном масштабе
горизонтальную и фронтальную
проекции сооружения
3.
Сущность метода проекций счисловыми отметками заключается в
том, что все точки предмета
проецируют под прямым углом
(ортогонально) на одну
горизонтально расположенную
плоскость проекций –
плоскость нулевого уровня (П0)
4.
Проекцию, служащую для полученияинформации о высоте точек предмета,
заменяют числами –
отметками
5.
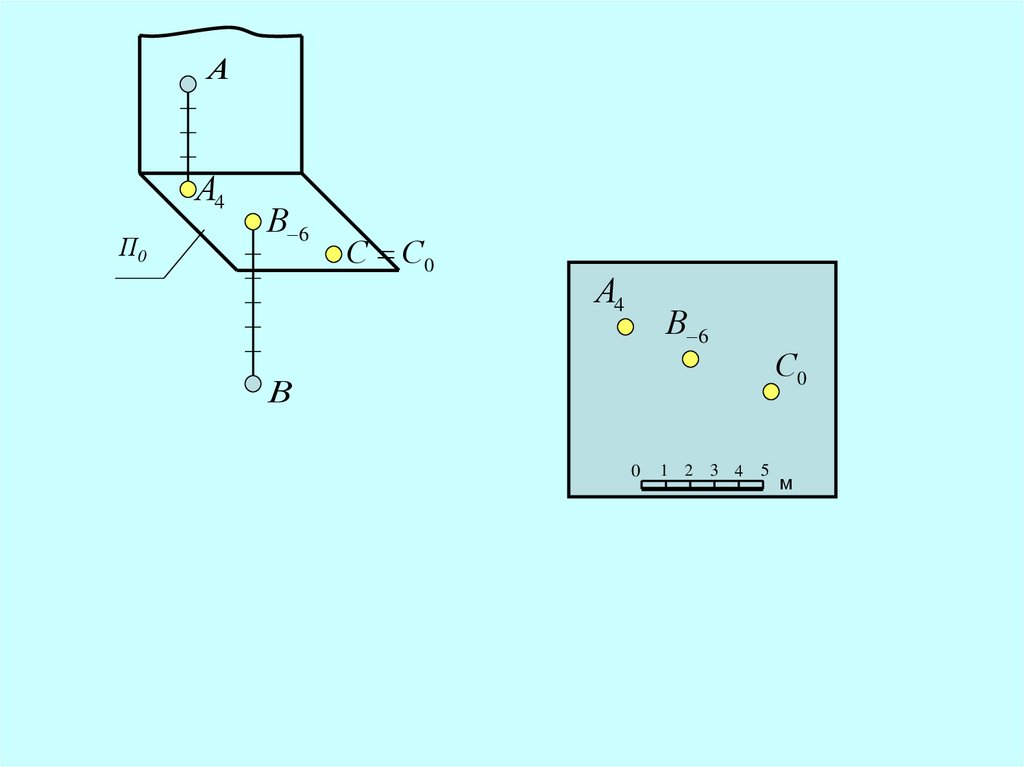
Проекции точки6.
АА4
П0
В 6
С С0
А4
В 6
С0
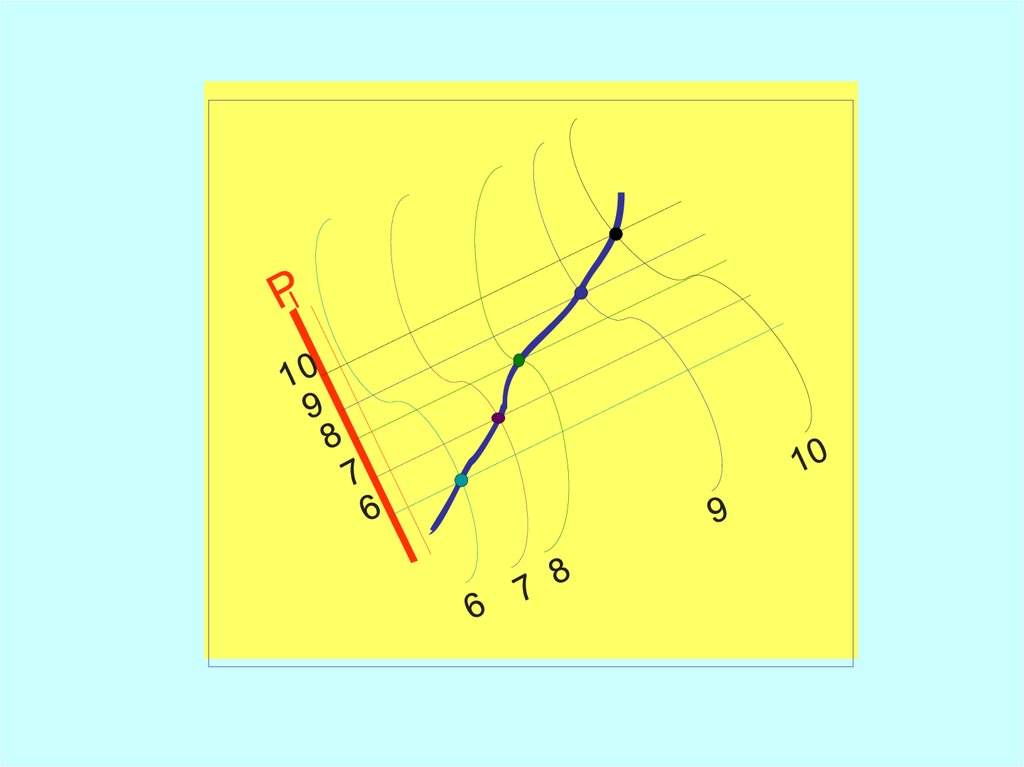
В
0
1 2
3 4 5
м
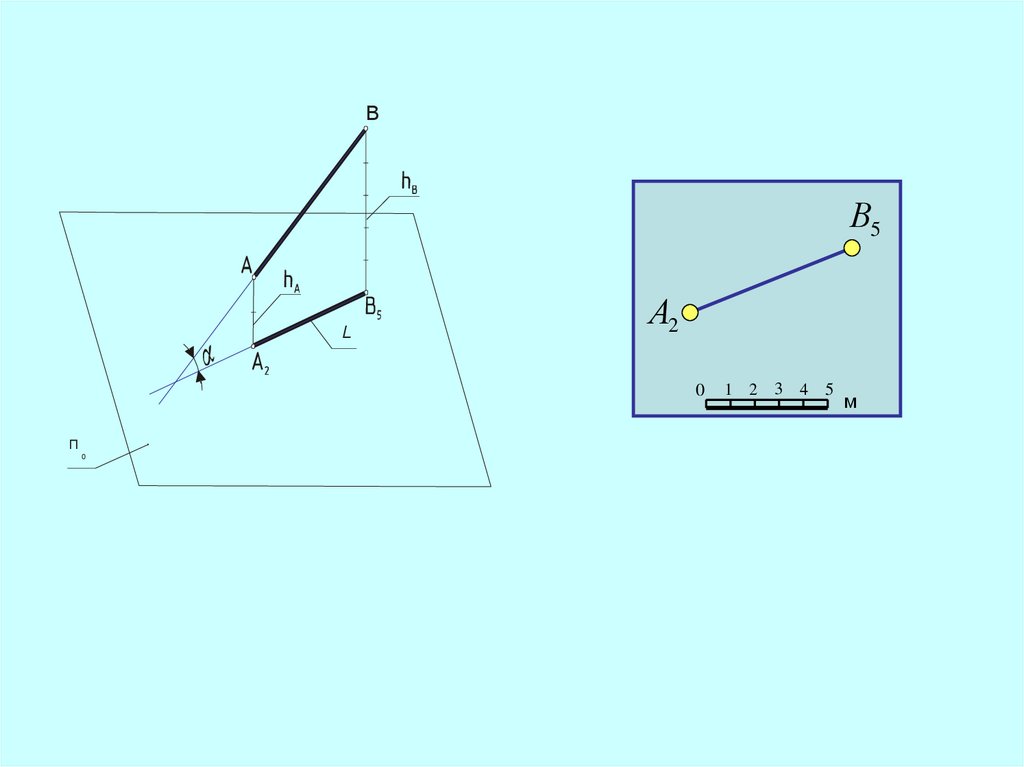
7.
Проекции прямой8.
ВВ5
L
А2
0
П
0
1 2
3 4 5
м
9.
Разность отметок концов отрезканазывается
превышением
отрезка прямой
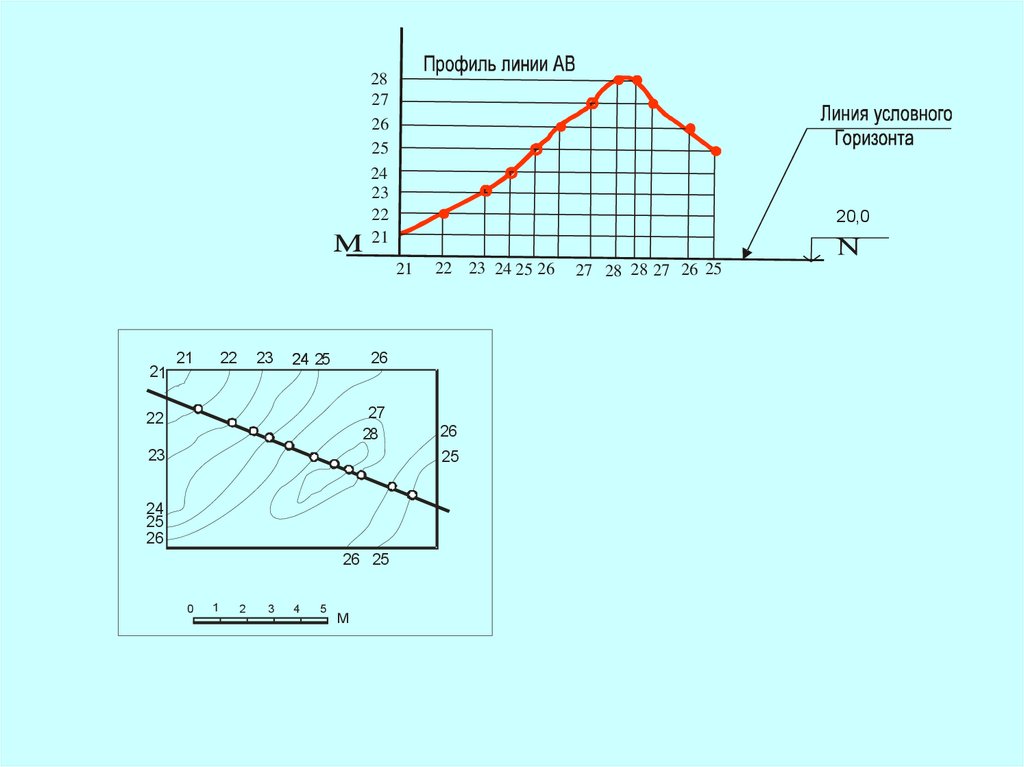
10.
Длина горизонтальной проекцииотрезка называется
заложением прямой
11.
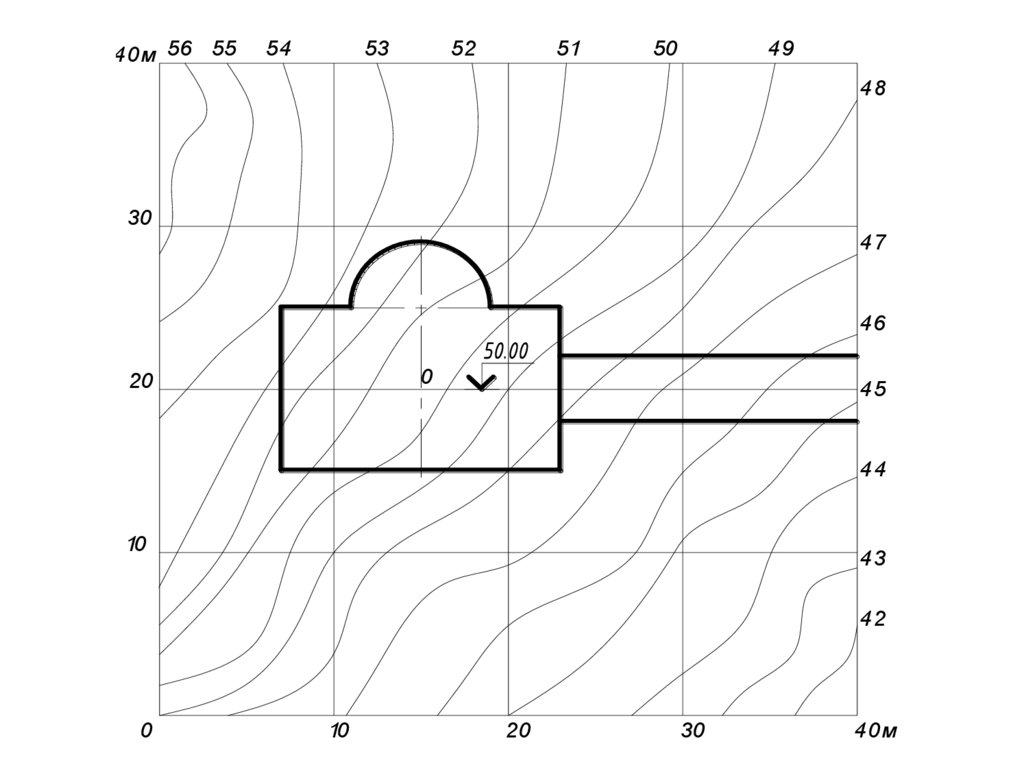
Отношение превышения прямой к еезаложению называется
уклоном прямой - ( i )
i
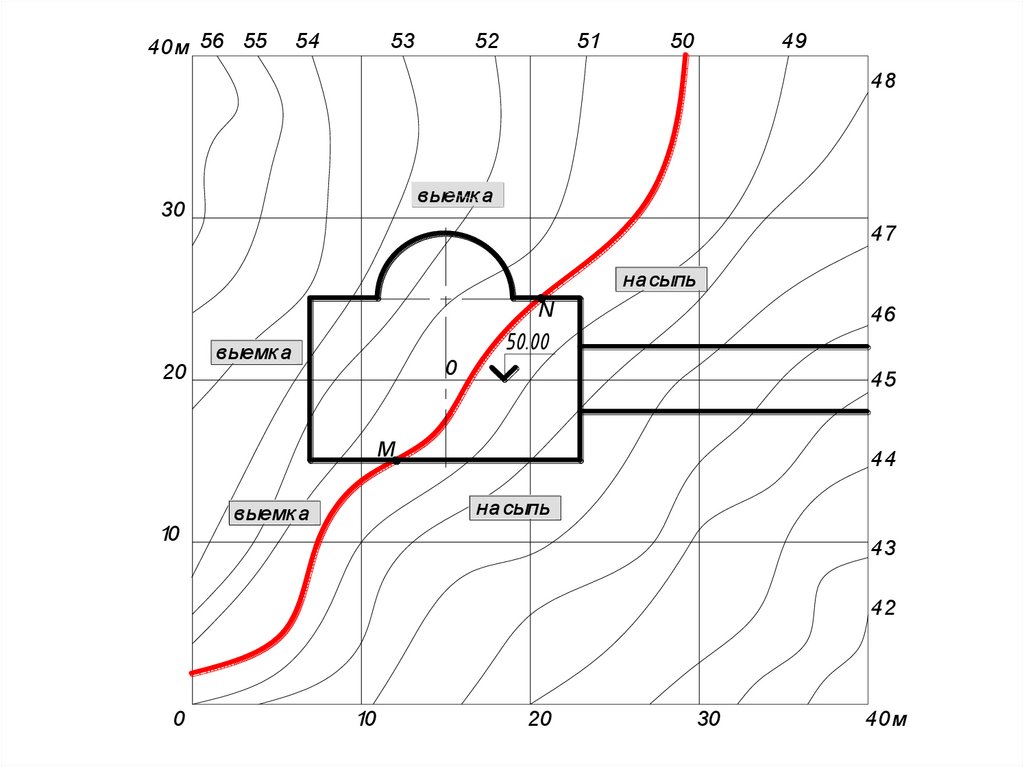
hB h A
L
12.
Численно уклон равен тангенсу угланаклона прямой к плоскости нулевого
уровня:
i = tg
Уклон может записываться в виде: отношения - 1:1, 1:2 и т.д.;
процентов - 15%, 20% и т.д.,
в виде градусов - 15 ,30 и т.д.
13.
Углом наклона прямойназывается острый угол между
прямой и ее проекцией на
плоскость нулевого уровня
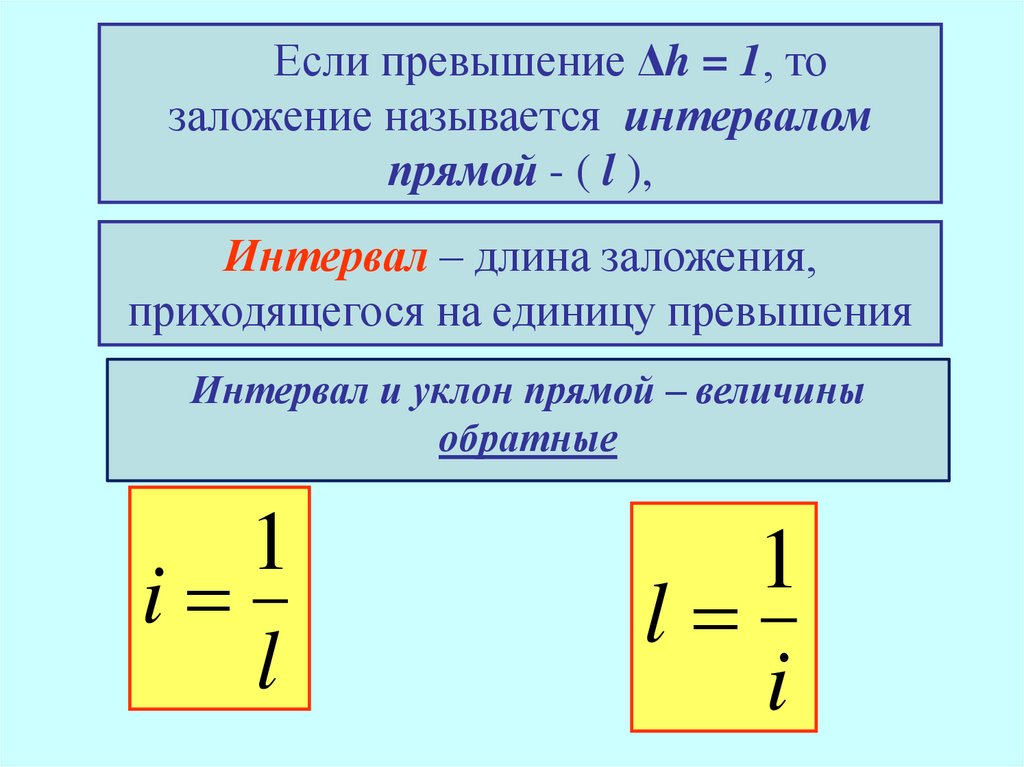
14.
Если превышение Δh = 1, тозаложение называется интервалом
прямой - ( l ),
Интервал – длина заложения,
i приходящегося на единицу превышения
Интервал и уклон прямой – величины
обратные
1
i
l
1
l
i
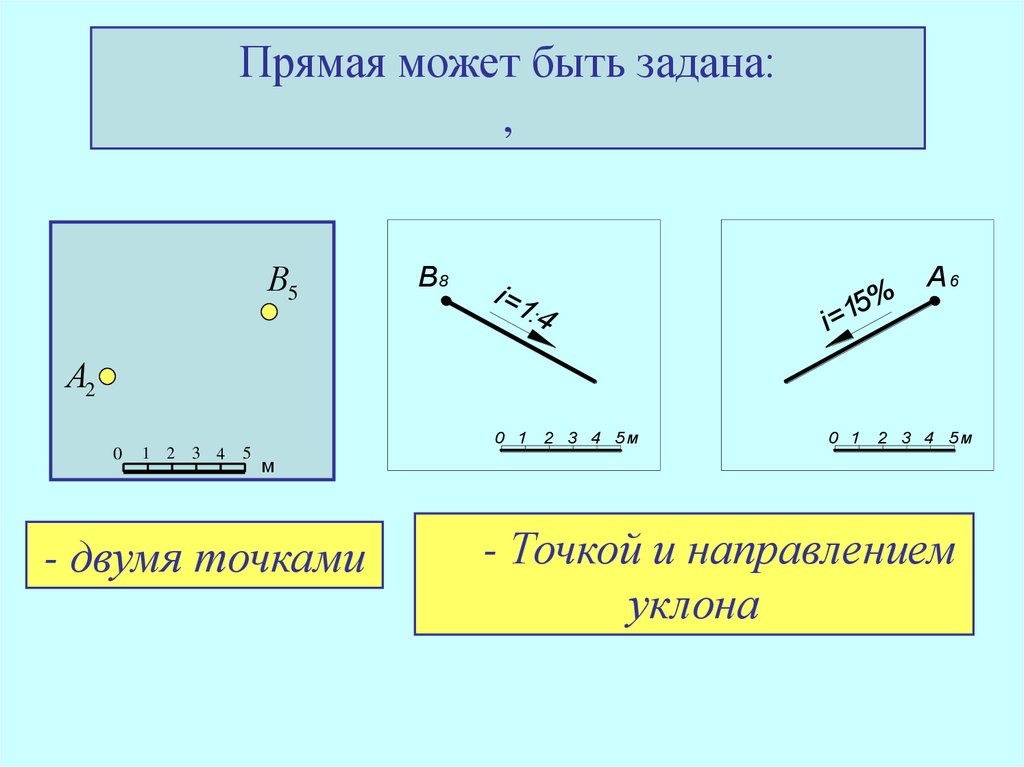
15.
Прямая может быть задана:,
В5
B8
i=1
:4
5%
1
=
i
А6
А2
0
1 2
3 4 5
0 1
2 3 4 5м
0 1
2 3 4 5м
м
- двумя точками
- Точкой и направлением
уклона
16.
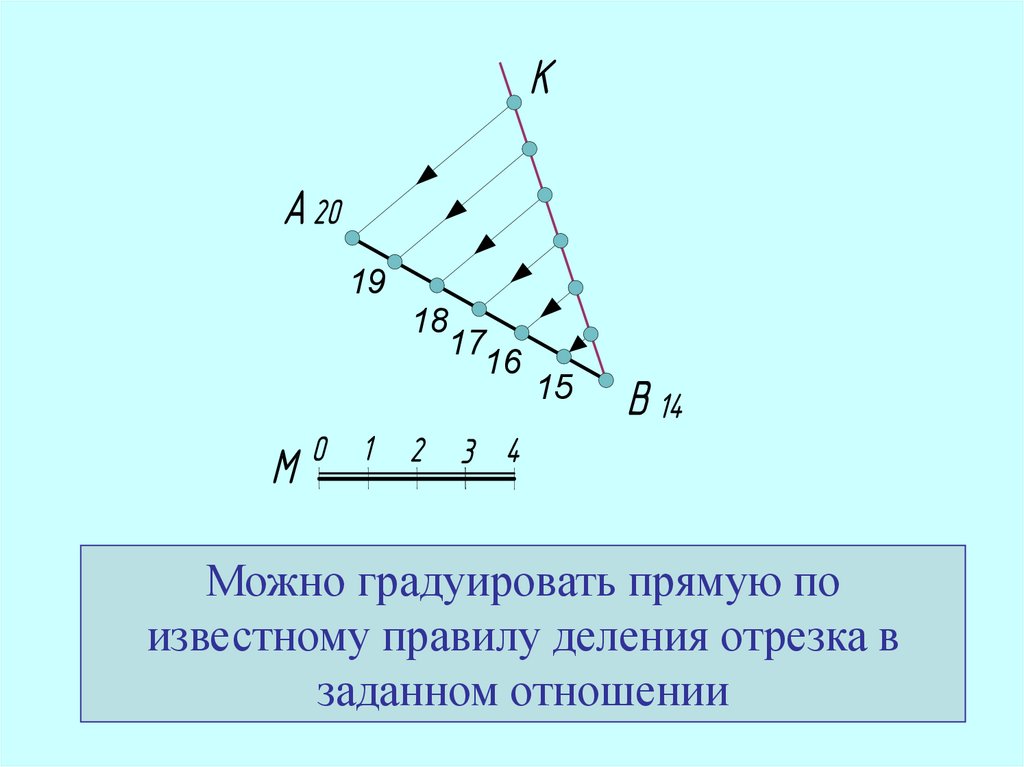
Градуирование прямой17.
При решении некоторых задач возникаетнеобходимость найти на прямой линии
точки с целыми отметками, эта операция
называется
градуированием прямой
(интерполированием)
18.
ЗадачаЗадан отрезок прямой АВ его
проекцией с числовыми отметками.
Необходимо провести
градуирование отрезка АВ
19.
1918
17
16
15
Можно градуировать прямую по
известному правилу деления отрезка в
заданном отношении
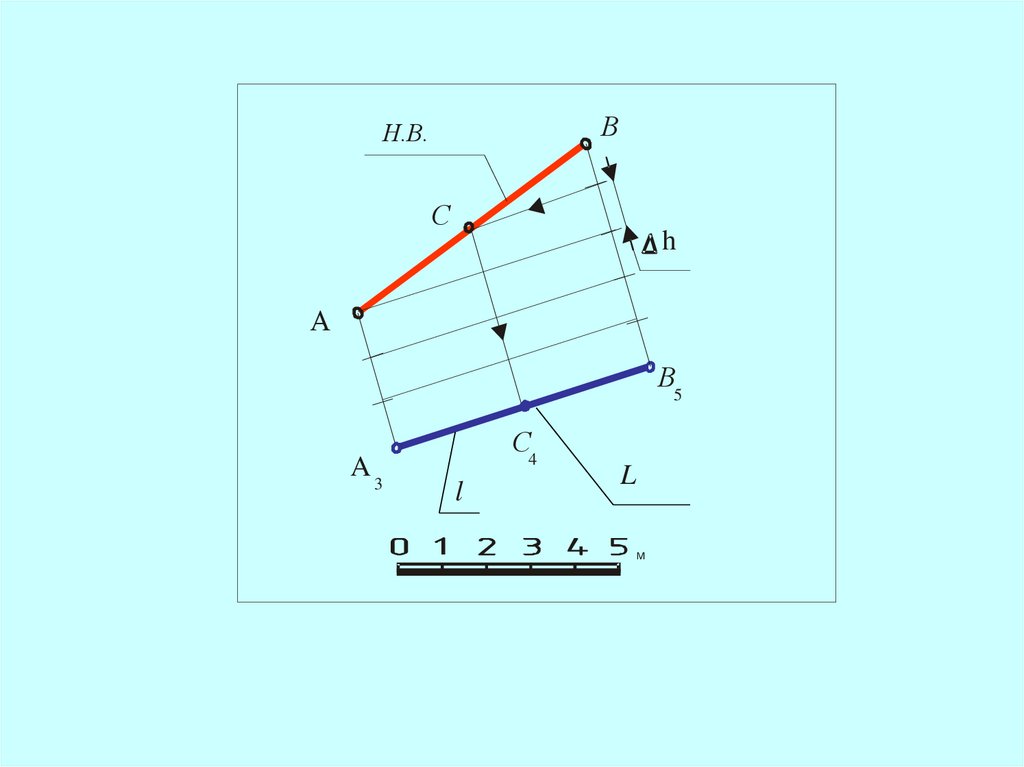
20.
Алгоритм:Определяют натуральную величину отрезка
На отрезке АВ находят точки с целыми
отметками,
(проведя из точек 2,3,4,5 прямые, параллельные проекции прямой)
Найденные на прямой АВ
точки II,III,IV,V, проецируют
на проекцию прямой
21.
ВН.В.
С
h
А
В5
A3
С4
l
L
М
22.
3. Полученный отрезок АВ и будетсоответствовать натуральной величине
заданного отрезка
4. Угол между отрезками АВ и А3 В5 равен
искомому углу наклона прямой ( ) к
плоскости нулевого уровня П0
По уклону прямой можно определить ее
интервал, а по интервалу – ее уклон
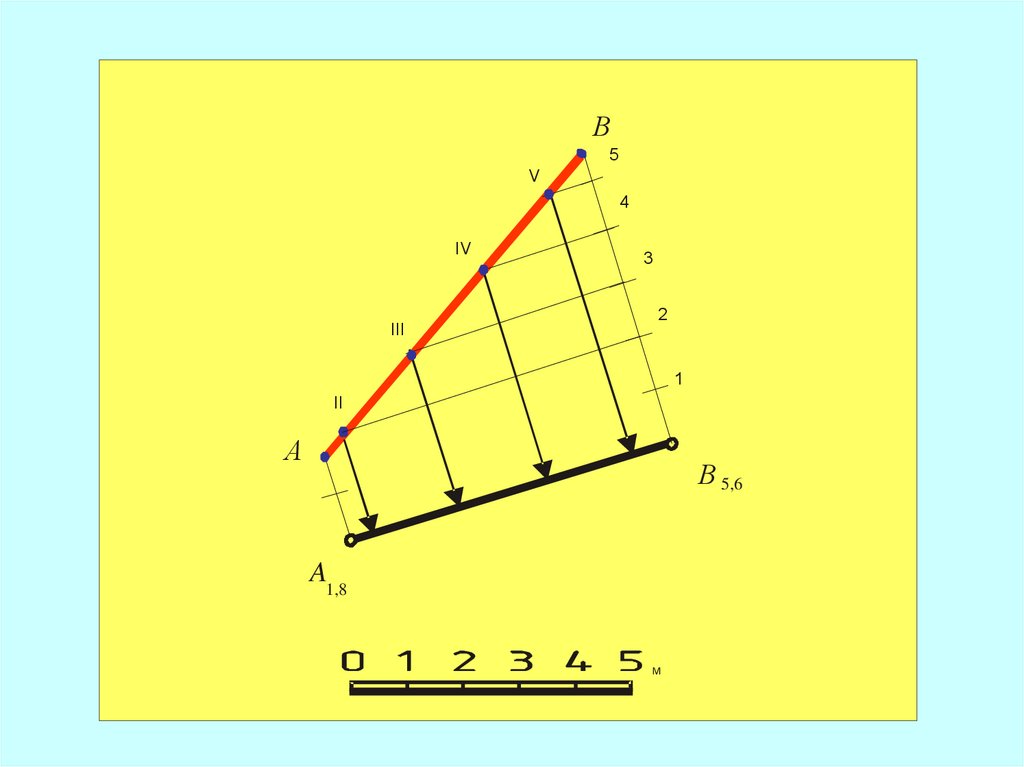
23.
Алгоритм градирования прямой сдробными отметками и нахождения НВ
отрезка
1. Из точек А1,8 и В5,6 восставляют
перпендикуляры к проекции прямой
2. На перпендикулярах откладывают
отрезки, равные соответственно 1,8 и 5,6
единицам длины
2. Полученный отрезок АВ и будет
соответствовать НВ заданного отрезка
24.
В5
V
4
IV
III
3
2
1
II
А
В 5,6
A1,8
М
25.
Положение прямых впространстве
26.
Прямая, не перпендикулярная и непараллельная плоскости проекций,
называется наклонной прямой
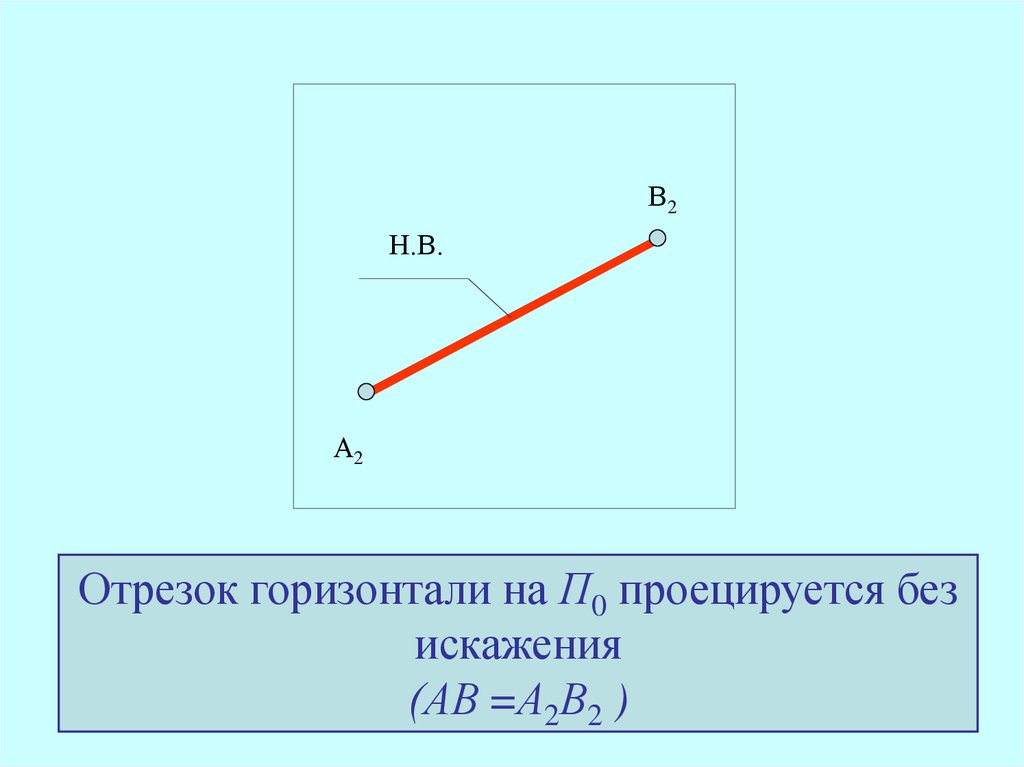
Если прямая АВ параллельна плоскости
нулевого уровня (АВ // П0),
то концы отрезка: точки А и В – имеют
одинаковые отметки
Такая прямая называется горизонталью
27.
В2Н.В.
А2
Отрезок горизонтали на П0 проецируется без
искажения
(АВ =А2В2 )
28.
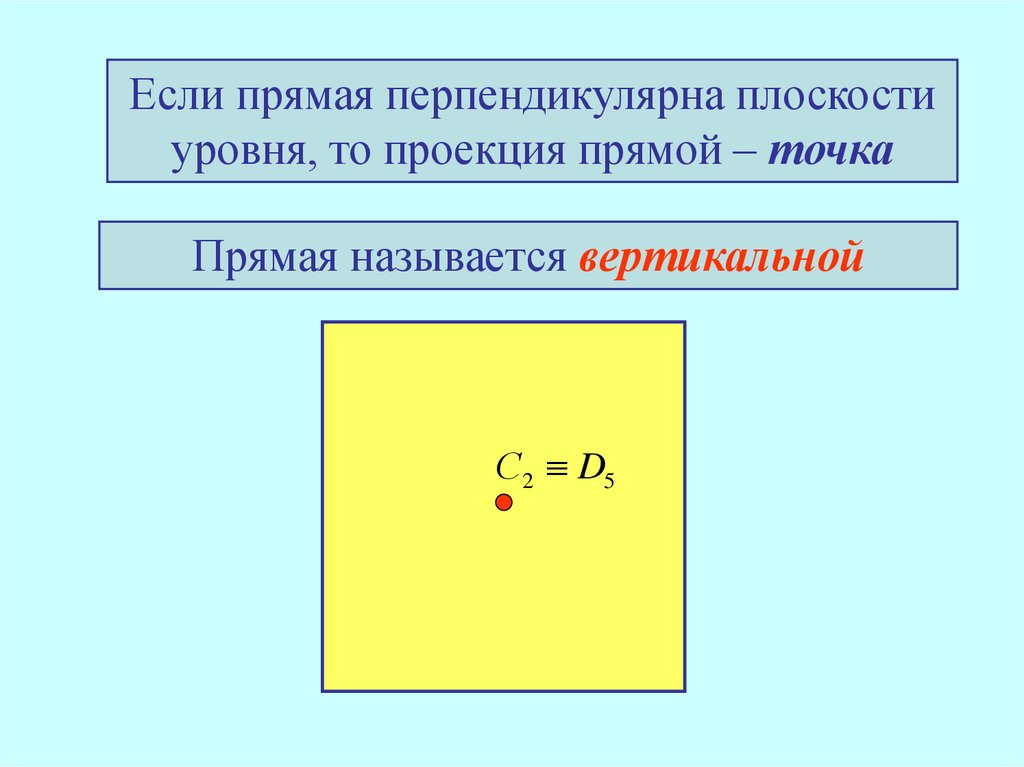
Если прямая перпендикулярна плоскостиуровня, то проекция прямой – точка
Прямая называется вертикальной
С2 D5
29.
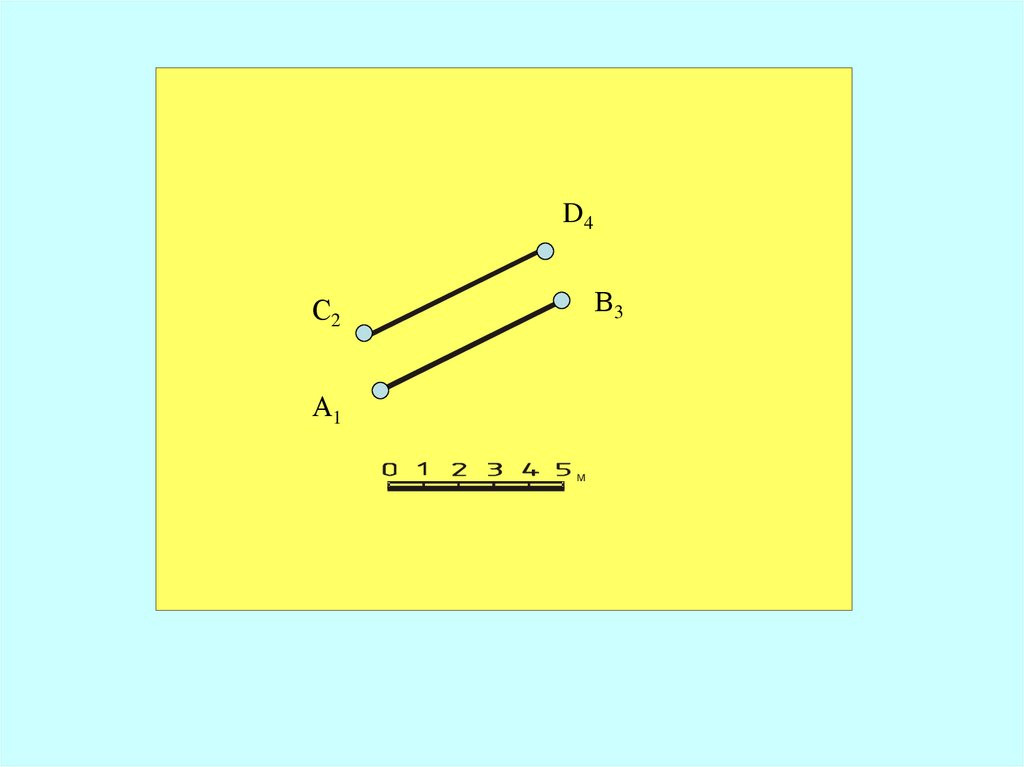
Если две прямые параллельныдруг другу, то их
проекции параллельны,
интервалы равны,
отметки возрастают в одном
направлении
30.
D4В3
С2
А1
М
31.
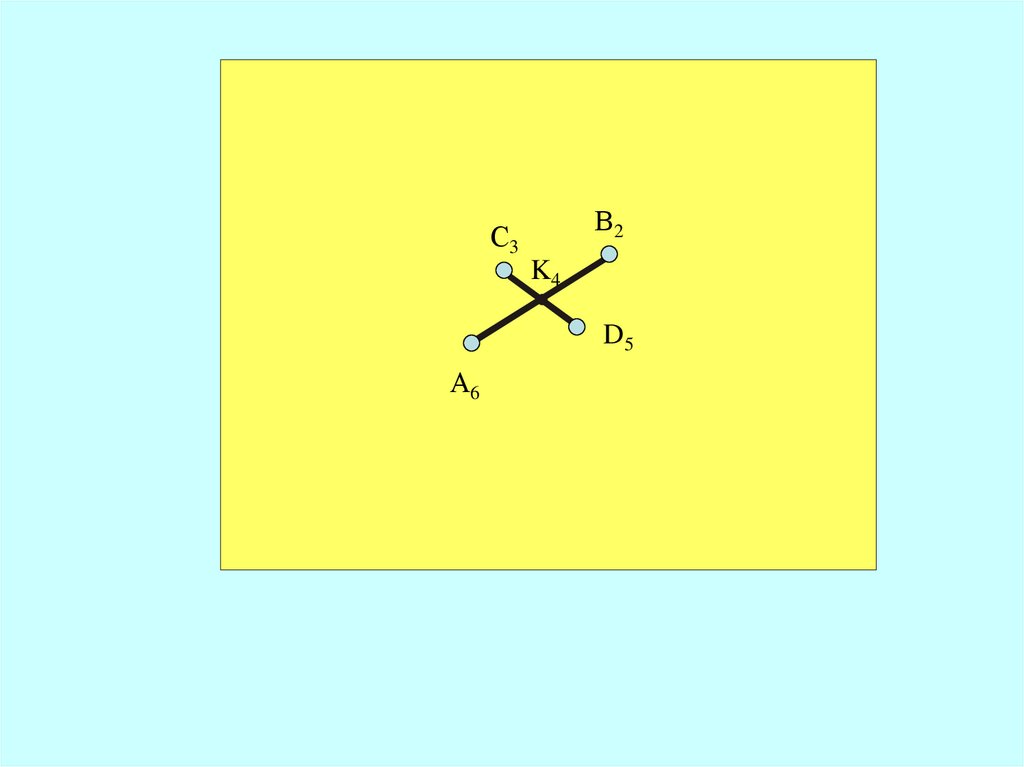
Если прямые пересекаются, то ихпроекции пересекаются,
а точка пересечения имеет
одну и ту же отметку
как на одной, так и на другой прямой
32.
В2С3
K4
D5
А6
33.
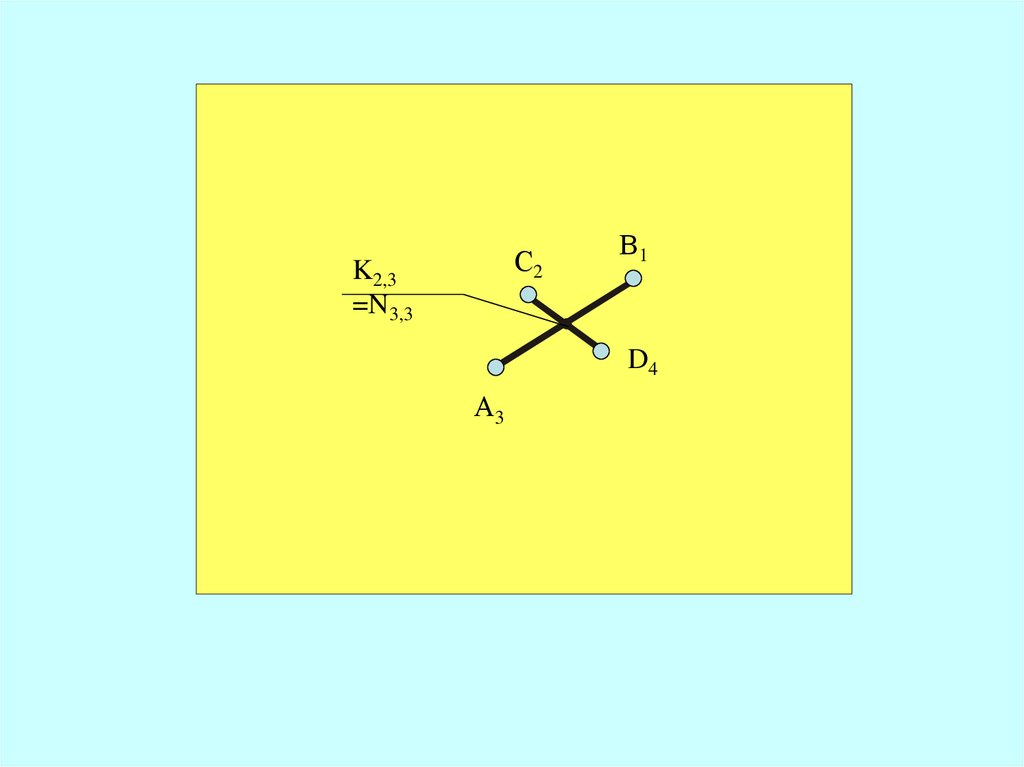
Если прямые скрещиваются, то ихпроекции могут пересекаться,
но точки на прямых
в месте пересечения их проекций
имеют разные отметки
34.
С2K2,3
=N3,3
В1
D4
А3
35.
Проекции скрещивающихся прямых могутбыть параллельны, но
интервалы и углы падения у них неравны,
а если интервалы равны, то
направления падения не совпадают
36.
Проекции плоскости37.
Плоскость в проекциях с числовымиотметками можно задать теми же
способами, что и в ортогональных
проекциях.
Но удобнее задавать ее положение в
пространстве масштабом уклона
(падения)
38.
Масштабом уклона(падения)
плоскости называется
проекция линии наибольшего наклона
(ската) плоскости,
на которой показываются отметки точек
39.
Линии наибольшего наклонавсегда перпендикулярны горизонталям
плоскости
По теореме о проецировании прямого угла
угол между масштабом уклона и проекцией
горизонтали на П0
будет равен 90º
Горизонталь с отметкой 0 называется
горизонтальным следом плоскости
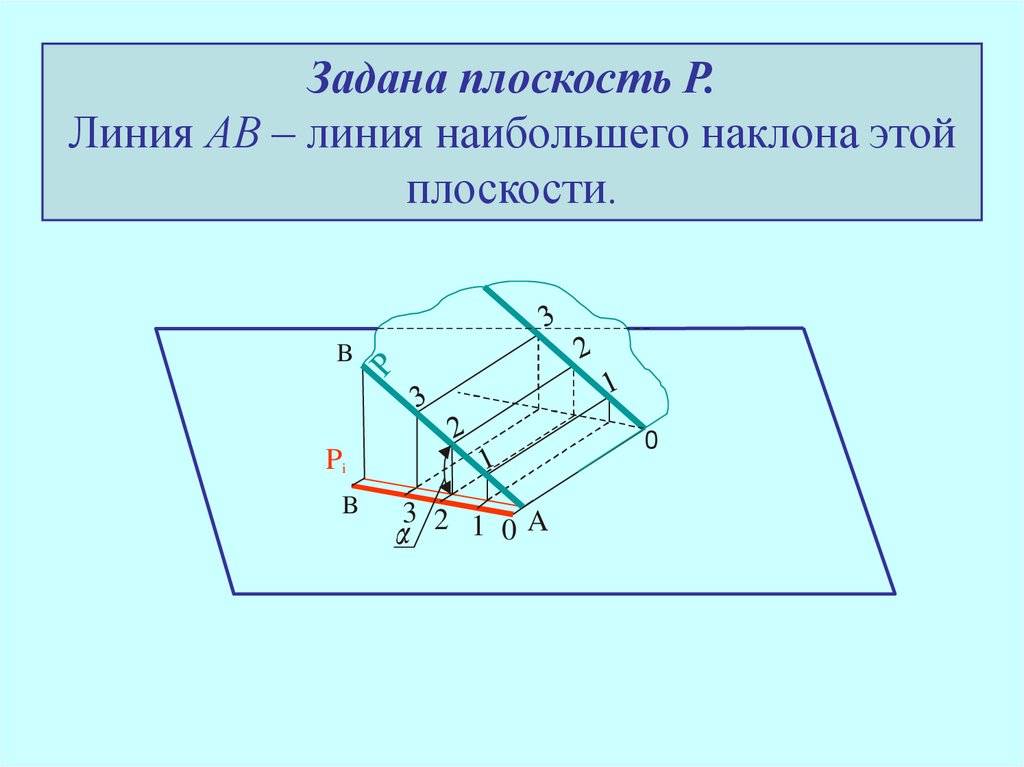
40.
Задана плоскость P.Линия АВ – линия наибольшего наклона этой
плоскости.
41.
Задана плоскость P.Линия АВ – линия наибольшего наклона этой
плоскости.
B
0
Pi
B
3 2 1 A
0
42.
Линия наибольшего наклона спроецируется наплоскость П0 в прямую,
которая и будет являться
масштабом уклона Рi плоскости Р.
Масштаб уклона плоскости принято чертить
двумя линиями:
сплошной толстой основной
и сплошной тонкой
43.
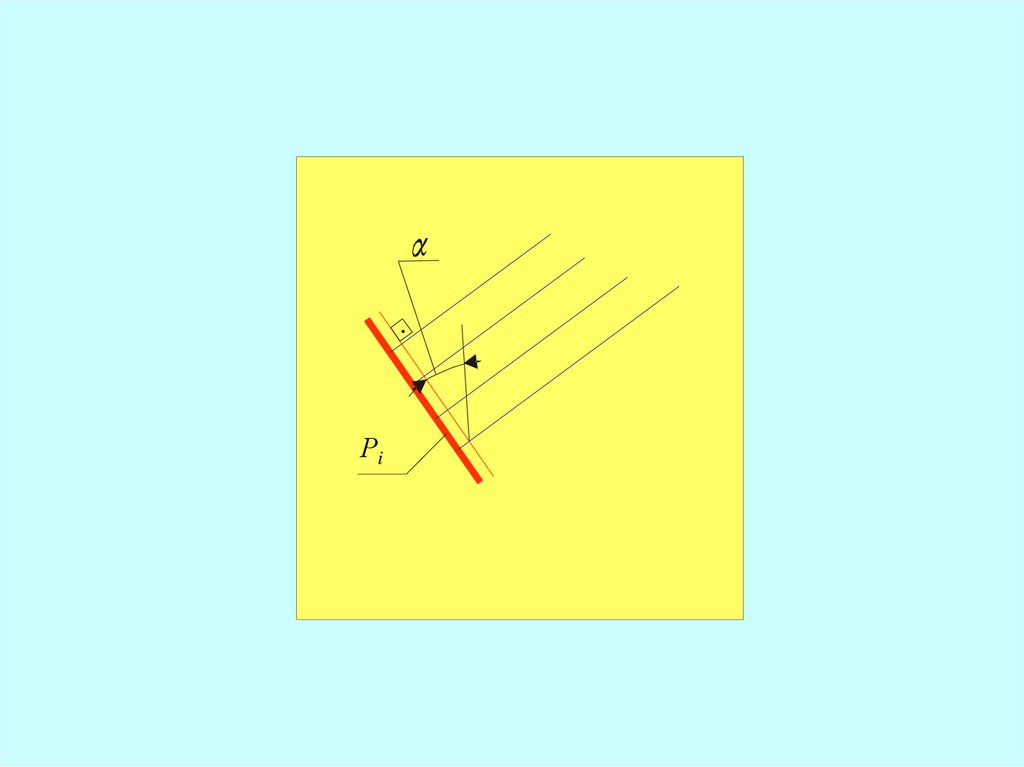
РiМ
44.
Масштаб уклона плоскости задаетсяперпендикулярно проекциям горизонтали
этой плоскости.
И если плоскость задана масштабом уклона,
то проекции горизонталей этой плоскости
всегда перпендикулярны масштабу уклона.
Угол между линией наибольшего наклона и
масштабом уклона называют
углом наклона плоскости (углом падения).
45.
Расстояние l между соседними проекциямигоризонталей (с целыми отметками)
называется
интервалом плоскости
46.
Взаимное расположениедвух плоскостей
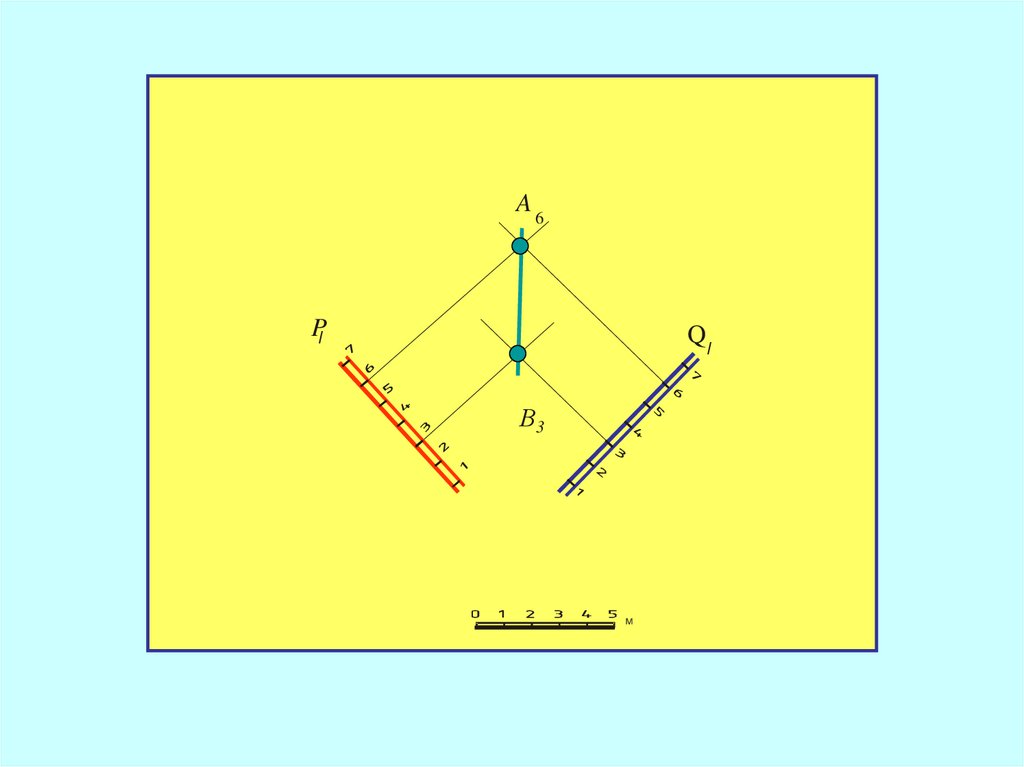
47.
Если плоскости пересекаются,то для определения их линии
пересечения
необходимо построить хотя бы две
точки пересечения их горизонталей,
имеющих одинаковые отметки
48.
A6PI
QI
В3
М
49.
Поверхности в проекциях счисловыми отметками
50.
Поверхности задаютсяхарактерными для данной поверхности
линиями
(прямыми или кривыми)
и числовыми отметками
основных ее точек
51.
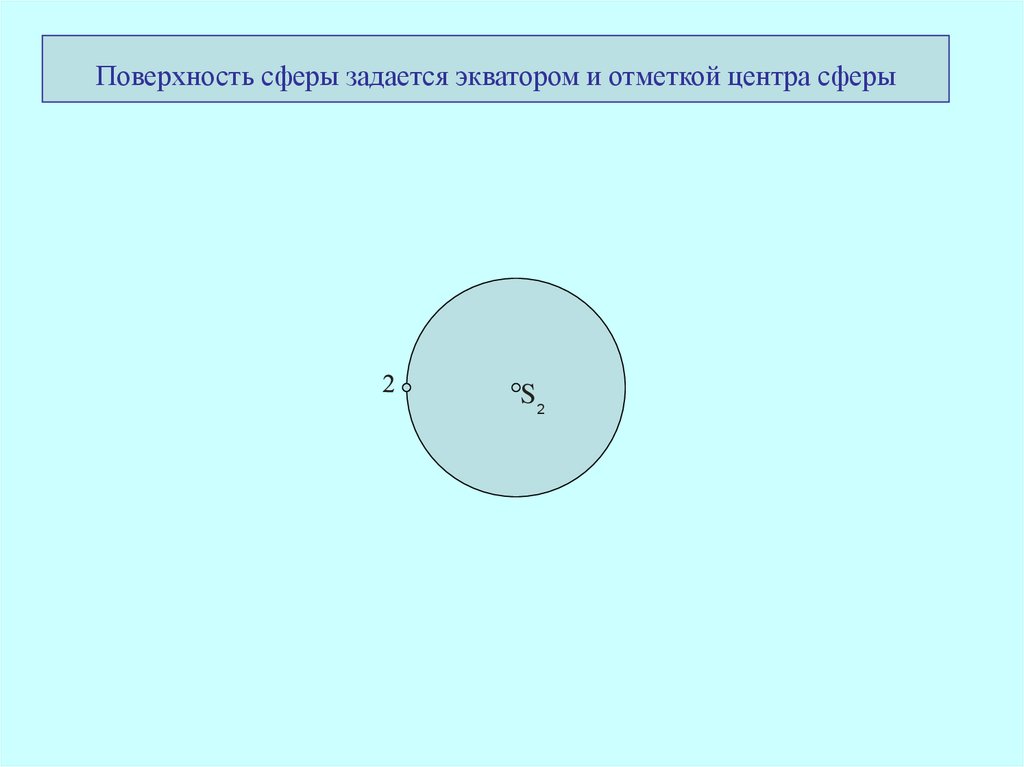
Поверхность сферы задается экватором и отметкой центра сферыS2
52.
Поверхность прямого кругового конуса задается сериейконцентрических окружностей через равные интервалы, их числовыми
отметками и отметкой вершины
S8
7
6
53.
Земная поверхность называетсятопографической
На чертежах топографическую поверхность
изображают совокупностью расположенных на
ней линий – горизонталей,
по которым она пересекается
горизонтальными плоскостями.
54.
Горизонтали соединяют точки поверхности с одинаковыми числовымиотметками
55.
Пересечениетопографической
поверхности
с плоскостью
56.
Для того, чтобы определить объемы играницы землянных работ, строят линию
пересечения откосов насыпей и выемок с
поверхностью земли, т.е.
строят линию пересечения плоскости откоса
с топографической поверхностью
57.
58.
Расстояние между плоскостями, которыепересекают топографическую поверхность,
называется
высотой сечения горизонталей
Ее указывают на чертеже и выбирают в зависимости от масштаба чертежа и
рельефа местности.
59.
Для составления подробных плановдополнительно к горизонтальной (опорной)
плоскости проекций используют
вертикальную плоскость и строят линию
пересечения ее с топографической
поверхностью, т.е. строят
профиль местности
60.
Например, пусть задана топографическая поверхность своимигоризонталями.
Требуется построить профиль поверхности, если плоскость его
проходит через прямую АВ, т.е. плоскость является вертикальной.
61.
АЛГОРИТМ РЕШЕНИЯ1. На линии АВ отмечают точки пересечения проекции вертикальной
плоскости с горизонталями поверхности
2. Переносят эти точки на горизонтальную прямую МN,отметку которой
принимают условно равной наименьшей отметке профиля или округляют
до еще меньшей отметки
(например, для данной задачи отметка MN равна 21,0)
3. На перпендикулярах к MN откладывают величины превышений
отмеченных точек горизонталей над линией условного горизонта
4. Полученные точки соединяют плавной кривой, которая и будет
являться искомым профилем данной поверхности
62.
2827
26
25
24
23
22
21
20,0
21
21
21
22
23
22 23 24 25 26
26
24 25
27
28
22
23
26
25
24
25
26
26 25
0
1
2
3
4
5
М
27 28 28 27 26 25
63.
ВИДЫ ЗЕМЛЯНЫХ СООРУЖЕНИЙРезультатом разработки грунта является земляное сооружение, представляющее
собой инженерное сооружение, устраиваемое из грунта в грунтовом массиве или
возводимое на поверхности грунта.
Земляные сооружения разделяют:
по отношению к поверхности грунта - выемки, насыпи, подземные
выработки, обратные засыпки;
по сроку службы — постоянные и временные;
по функциональному назначению - котлованы, траншеи, ямы, скважины,
отвалы, плотины, дамбы, дорожные полотна, туннели, планировочные площадки,
выработки;
по геометрическим параметрам и пространственной форме - глубокие,
мелкие, протяженные, сосредоточенные, простые, сложные и т. п.
64.
ЗАДАЧА:Дано: топографическая поверхность и земляное
сооружение (площадка) М 1:1000
Уклон откосов выемок - 1:3,
Уклон откосов насыпей - 1:3
Построить: линии пересечения откосов выемок
и насыпей земляного сооружения (площадки)
между собой и топографической поверхностью
65.
40м 56 5554
53
52
51
50
49
48
30
47
46
0
20
45
44
10
43
42
0
10
20
30
40м
66.
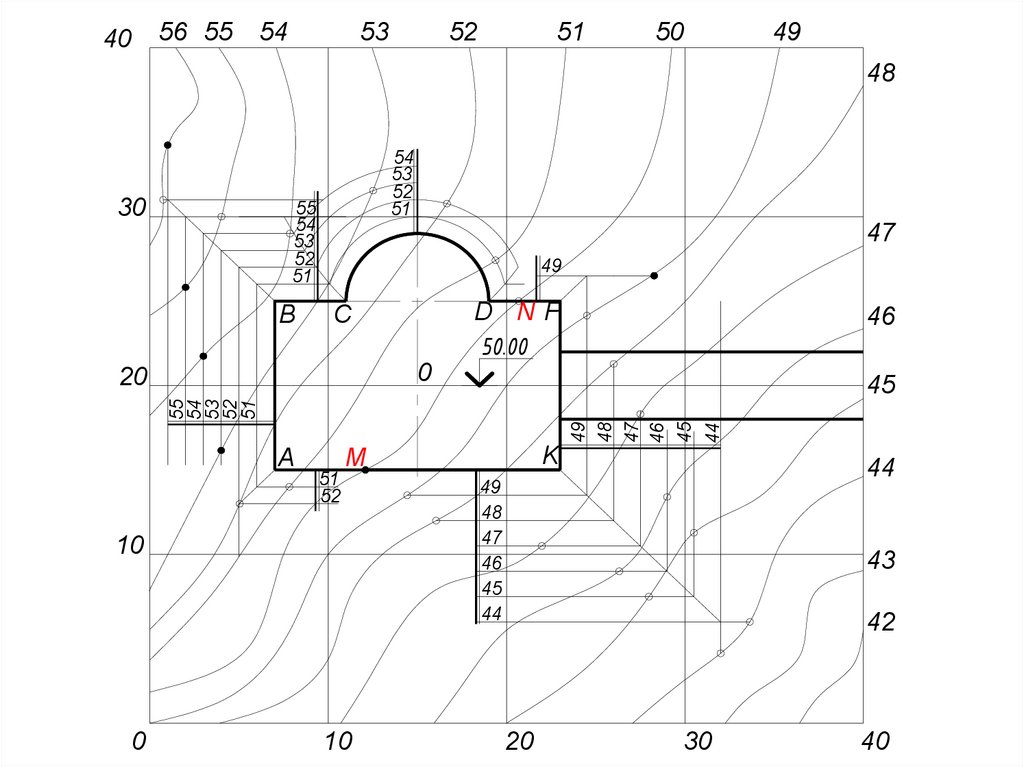
ПОРЯДОКВЫПОЛНЕНИЯ ЗАДАНИЯ
1. Нанести на чертеж изображения площадки
Определить нулевые работы и направления
работ по выемке и насыпи
2. Определить интервалы, М1:1000
• lв = 1:3=3 мм
• lн = 1:3 =3 мм
67.
40м 56 5554
53
52
51
50
49
48
выемка
30
47
насыпь
N
20
выемка
46
0
45
M
44
насыпь
выемка
10
43
42
0
10
20
30
40м
68.
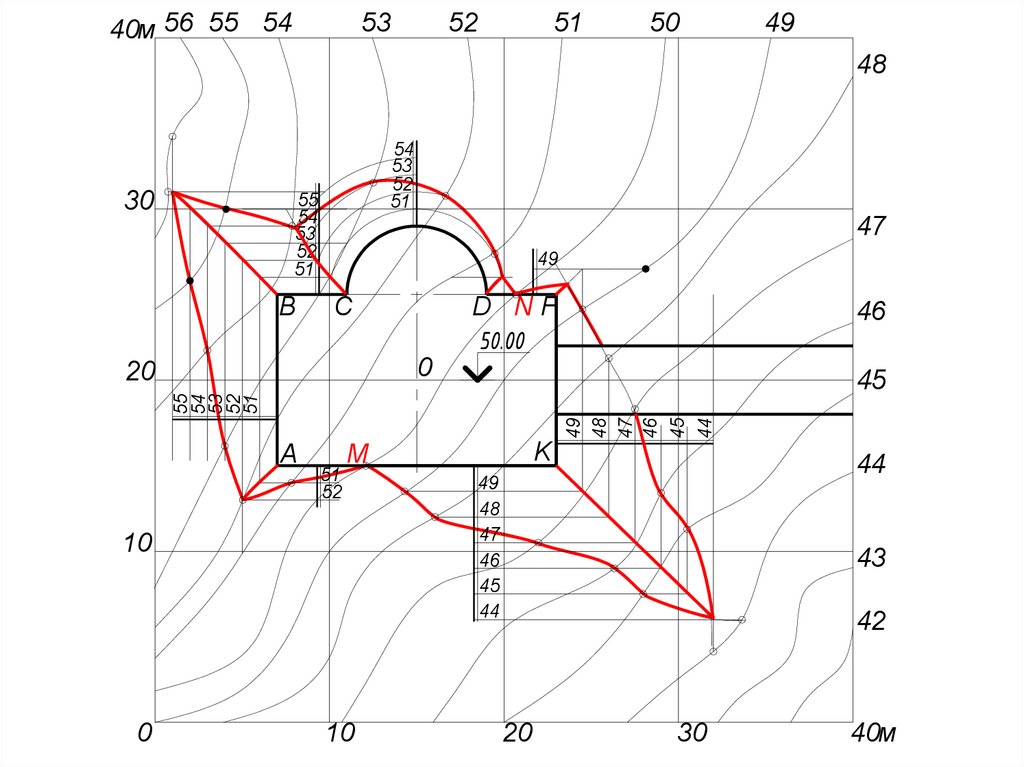
ПОРЯДОКВЫПОЛНЕНИЯ ЗАДАНИЯ
3. Определить линии пересечения смежных откосов
(Решение задачи: проведение плоскостей через отрезки
прямых и проведение поверхностей через дуги кривых с
заданным уклоном, ограничивающих площадку в плане.
Плоскости и поверхности, ограничивающие строительную
площадку со всех сторон и соединяющие ее с поверхностью
местности, называются откосами)
3. Построить границы земляных работ, т.е. линий
пересечения откосов выемки и насыпи с
топографической поверхностью
69.
4056 55
54
53
52
51
50
49
48
30
54
53
52
51
55
54
53
52
51
B
47
49
D NF
C
46
0
45
A
10
0
K
M
51
52
10
45
44
49
48
47
46
55
54
53
52
51
20
44
49
48
47
46
45
44
43
42
20
30
40
70.
40м 56 55 5453
52
51
50
49
48
30
54
53
52
51
55
54
53
52
51
В
47
49
С
D NF
46
0
45
49
48
47
46
45
44
55
54
53
52
51
20
A
51
52
10
0
K
M
10
44
49
48
47
46
45
44
43
42
20
30
40м
71.
40ì 56 5554
53
52
51
50
49
48
E
55
54
53
52
51
49
D NF
C
0
45
49
48
47
46
45
44
55
54
53
52
51
20
46
48
B
47
49
30
54
53
52
51
A
K
M
51
52
10
44
49
48
47
46
45
44
43
42
E
0
10
20
30
40ì
72.
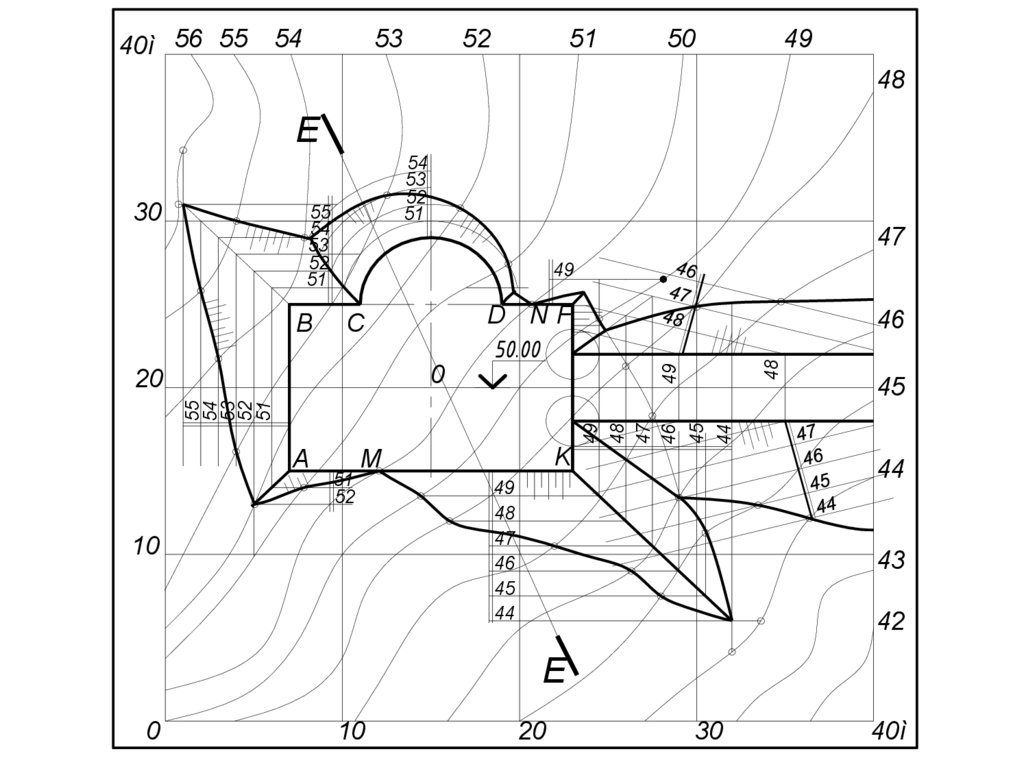
Линии построения(в том числе проектные
горизонтали) должны иметь толщину - 0,1...0,2мм
Контур земляного сооружения и линии пересечения
откосов с топографической поверхностью и между
собой обводят линиями толщиной -0,6-0,8мм
Для более наглядного выражения направления ската
насыпи
и
выемки
наносят
бергштрихи
перпендикулярно горизонталям плоскостей откосов
БЕРГШТРИХИ выполняют линиями разной длины,
толщиной- 0,1…0,2мм при расстоянии между
штрихами 1,5….2,5мм. Короткие штрихи должны
иметь длину, примерно равную половине длинных
штрихов
73.
PR
S
S
L
T
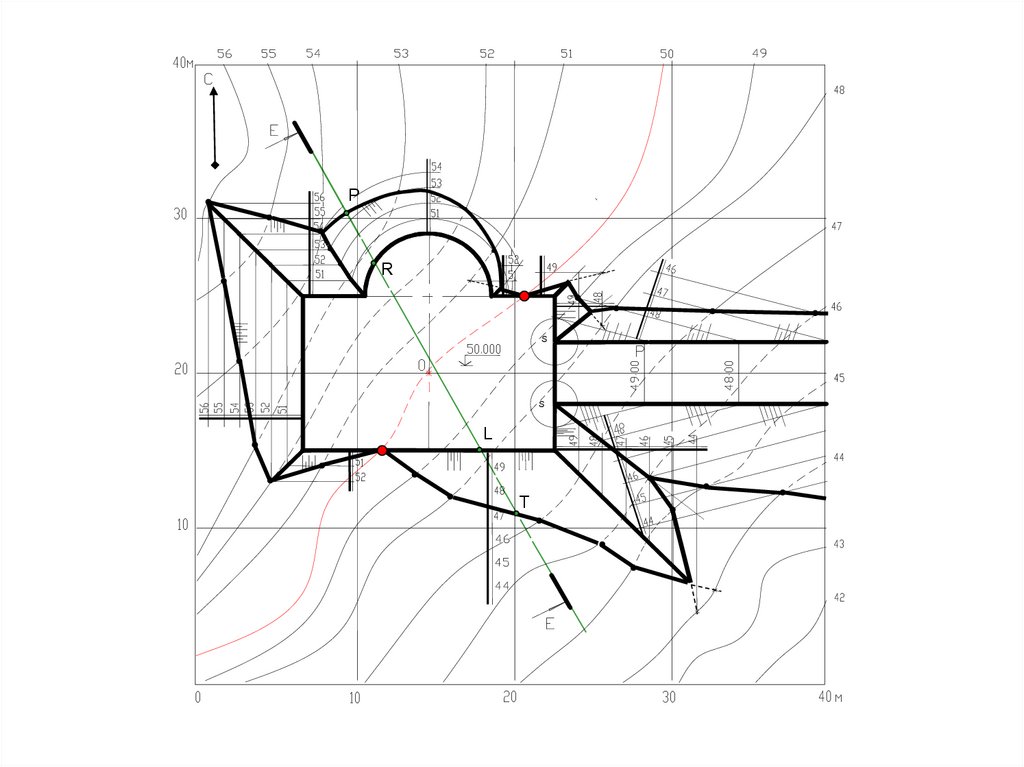
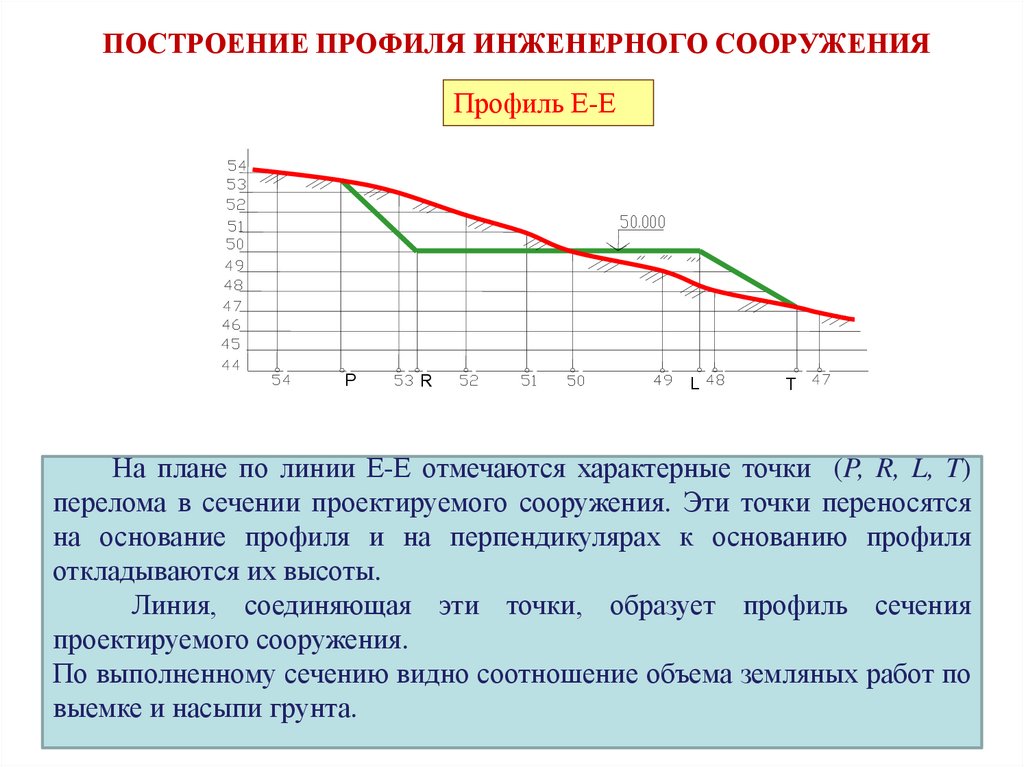
74. ПОСТРОЕНИЕ ПРОФИЛЯ ИНЖЕНЕРНОГО СООРУЖЕНИЯ
Профиль Е-ЕP
R
L
T
На плане по линии Е-Е отмечаются характерные точки (P, R, L, T)
перелома в сечении проектируемого сооружения. Эти точки переносятся
на основание профиля и на перпендикулярах к основанию профиля
откладываются их высоты.
Линия, соединяющая эти точки, образует профиль сечения
проектируемого сооружения.
По выполненному сечению видно соотношение объема земляных работ по
выемке и насыпи грунта.

















































 drafting
drafting








