Similar presentations:
Проекции с числовыми отметками. Лекция 29
1. Лекция 29
Проекции с числовыми отметкамиПринципы и аппарат проецирования
Проекции точки, прямой, плоскости
Градуирование прямой
Понятия уклона и интервала прямой
Взаимное расположение прямых
Геометрическая модель плоскости и способы ее
задания. Масштаб уклона плоскости
• Взаимное расположение точек , прямых и плоскостей
• Проекции поверхностей
2.
Проектирование и строительство жилых, общественныхи промышленных зданий не может осуществляться
без инженерной подготовки и благоустройства
городских территорий. Такие сооружения, как
магистрали и транспортные развязки, путепроводы и
мосты, набережные и подземные переходы являются
неотъемлемыми элементами современного города.
В процессе проектирования зданий и сооружений
составляют чертежи, на которых изображается
спланированная земная поверхность.
Проектирование сооружений, чтение и выполнение
чертежей требует знания специального способа
изображения- метода проекций с числовыми
отметками
3. Аппарат проецирования в проекциях с числовыми отметками
Если размеры проецируемого объекта ввертикальном направлении малы по сравнению с
размерами в горизонтальных направлениях,
целесообразно применять метод с числовыми
отметками. Данный метод требует построение
только одной проекции- на горизонтальную
плоскость П, которую называют «нулевой» (за
«абсолютный нуль» в нашей стране принят
уровень Балтийского моря у Кронштадта).
С помощью метода с числовыми отметками
изображается рельеф местности, нанесенные на
нем дороги, а также решаются многие задачи по
проектированию земляных сооружений, посадке
объектов на рельеф, определению объема
земляных работ и другие.
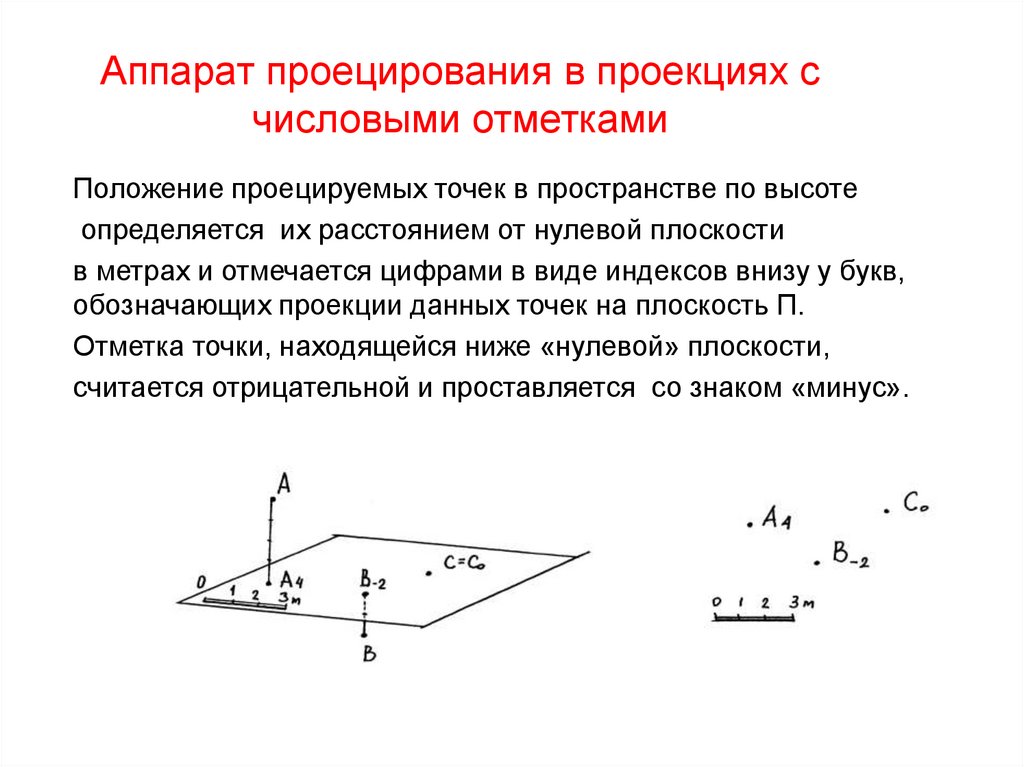
4. Аппарат проецирования в проекциях с числовыми отметками
Положение проецируемых точек в пространстве по высотеопределяется их расстоянием от нулевой плоскости
в метрах и отмечается цифрами в виде индексов внизу у букв,
обозначающих проекции данных точек на плоскость П.
Отметка точки, находящейся ниже «нулевой» плоскости,
считается отрицательной и проставляется со знаком «минус».
5. Геометрическая модель прямой
Прямая может быть задана:1. проекциями с числовыми отметками двух ее точек
2. одной точкой с числовой отметкой, направлением
горизонтальной проекции этой прямой и тангенсом
угла её наклона к плоскости По.
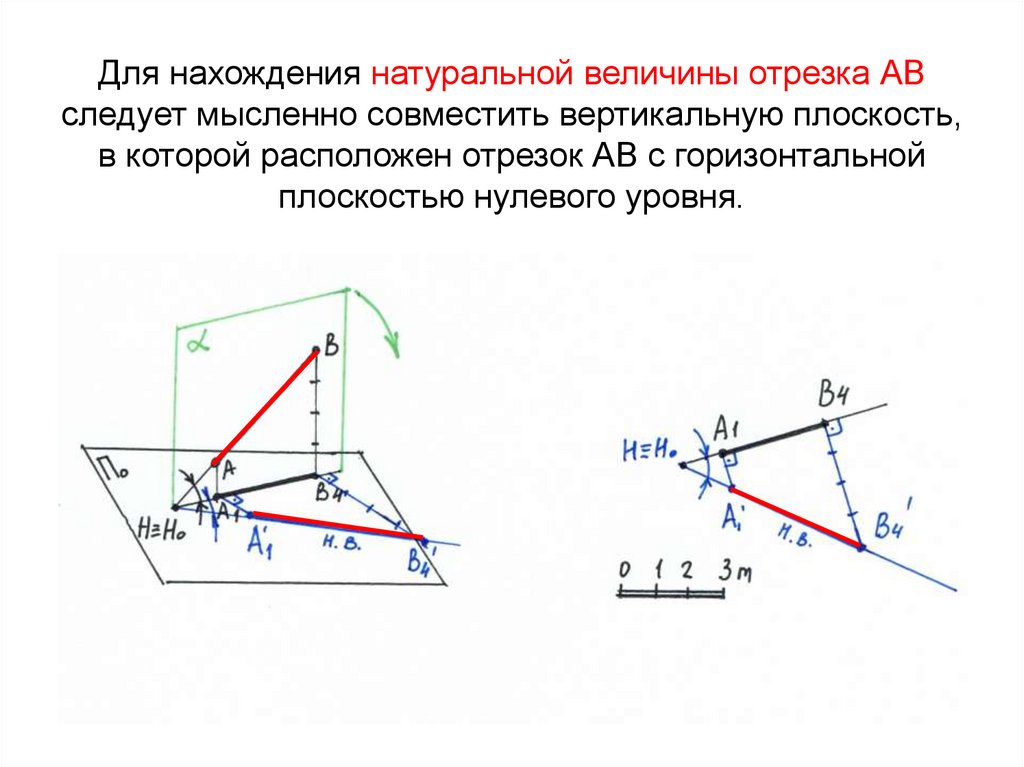
6. Для нахождения натуральной величины отрезка АВ следует мысленно совместить вертикальную плоскость, в которой расположен отрезок
АВ с горизонтальнойплоскостью нулевого уровня.
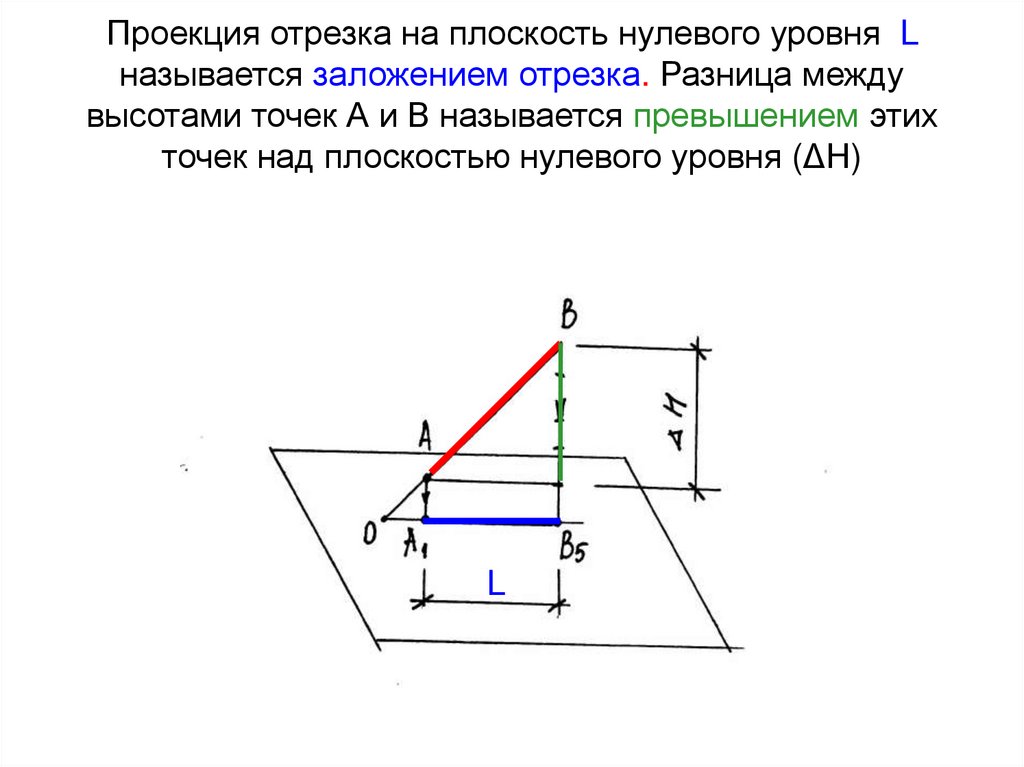
7. Проекция отрезка на плоскость нулевого уровня L называется заложением отрезка. Разница между высотами точек А и В называется
превышением этихточек над плоскостью нулевого уровня (ΔΗ)
L
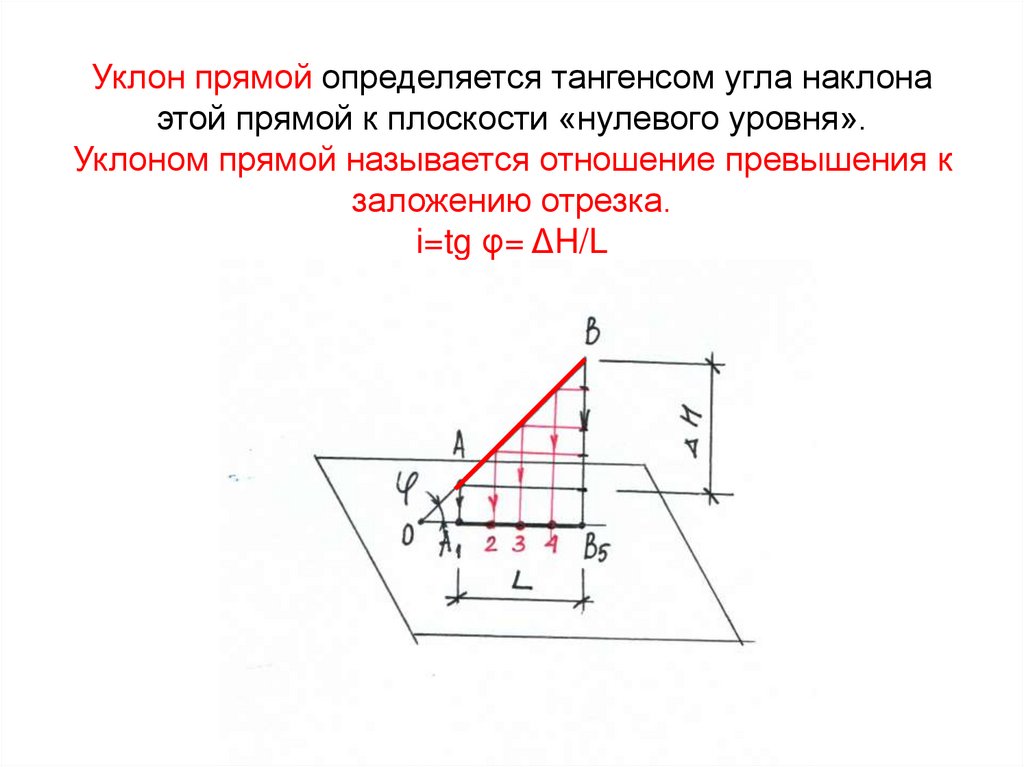
8. Уклон прямой определяется тангенсом угла наклона этой прямой к плоскости «нулевого уровня». Уклоном прямой называется отношение
превышения кзаложению отрезка.
i=tg φ= ΔH/L
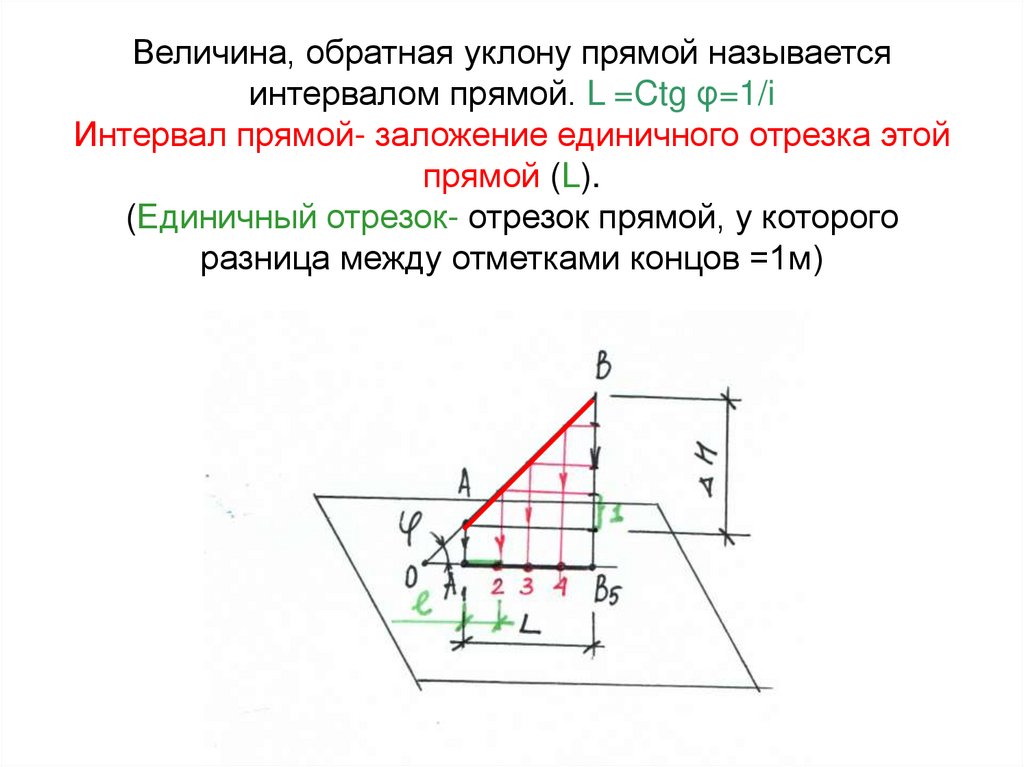
9. Величина, обратная уклону прямой называется интервалом прямой. L =Ctg φ=1/i Интервал прямой- заложение единичного отрезка этой
прямой (L).(Единичный отрезок- отрезок прямой, у которого
разница между отметками концов =1м)
10.
Определение натуральной величины отрезка прямой иугла его наклона к плоскости нулевого уровня
Задача 6.1 стр.48:
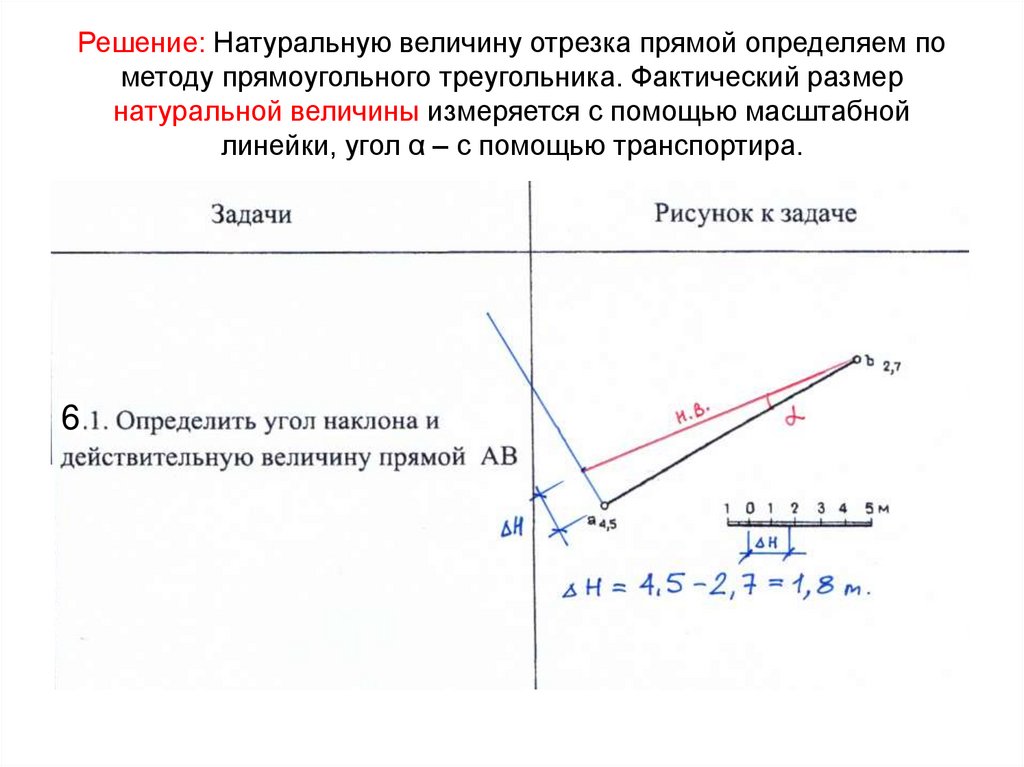
11. Решение: Натуральную величину отрезка прямой определяем по методу прямоугольного треугольника. Фактический размер натуральной
величины измеряется с помощью масштабнойлинейки, угол α – с помощью транспортира.
6
12. Градуирование прямой
Прямая может быть задана точками, имеющимидробные числовые отметки, а для решения целого
ряда задач удобно иметь отметки точек прямой,
выраженные целыми числами.
Отыскание на проекции заданного отрезка точек,
отметки которых равны целым числам и отличаются
на единицу от отметок рассматриваемых соседних
точек, называется градуированием прямой.
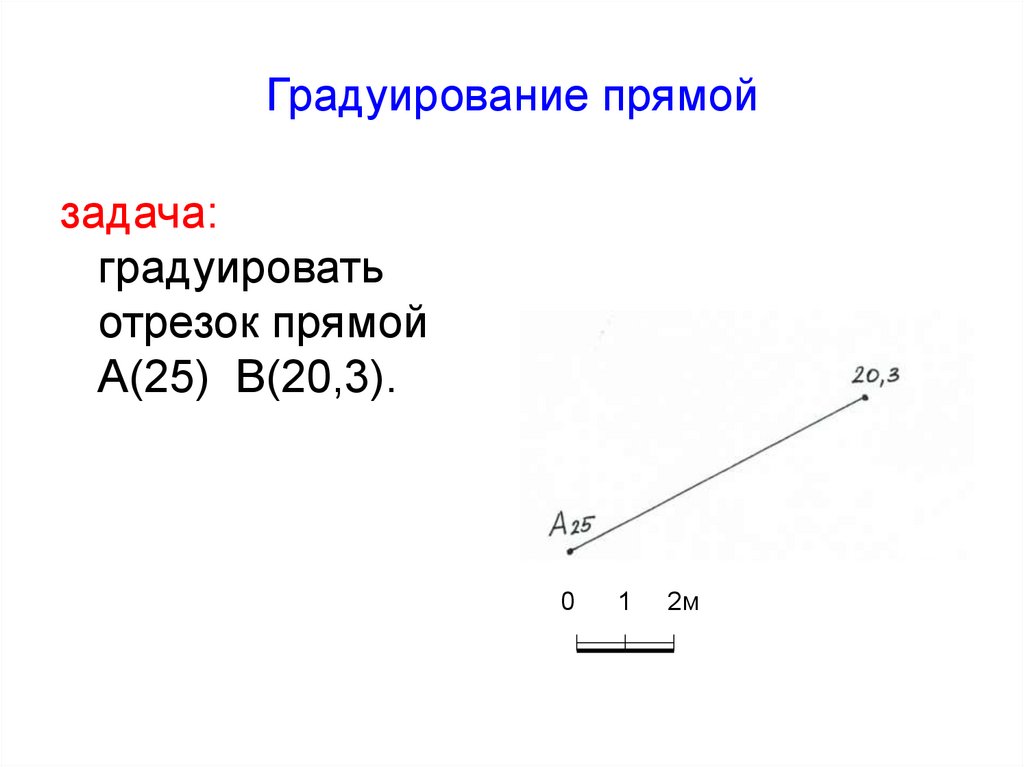
13. Градуирование прямой
задача:градуировать
отрезок прямой
А(25) В(20,3).
0
1
2м
14.
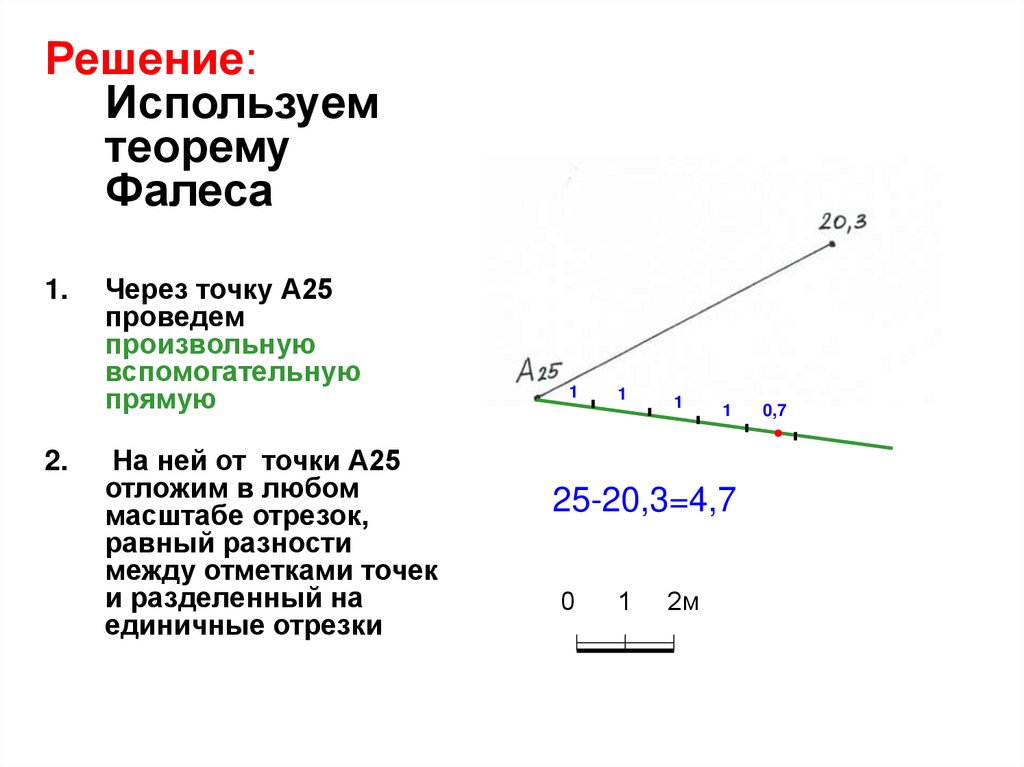
Решение:Используем
теорему
Фалеса
1.
2.
Через точку А25
проведем
произвольную
вспомогательную
прямую
На ней от точки А25
отложим в любом
масштабе отрезок,
равный разности
между отметками точек
и разделенный на
единичные отрезки
1
1
1
1
25-20,3=4,7
0
1
2м
0,7
15.
3. Соединим последнююточку полученной
пропорции, отложенной
на вспомогательной
прямой, с концом отрезка
точкой В 20,3. Т.о.
получим линию
пропорционального
переноса.
4.С помощью прямых,
параллельных линии
переноса, определим на
заданной проекции
прямой точки
с
целыми числовыми
отметками :
24, 23,
22, 21.
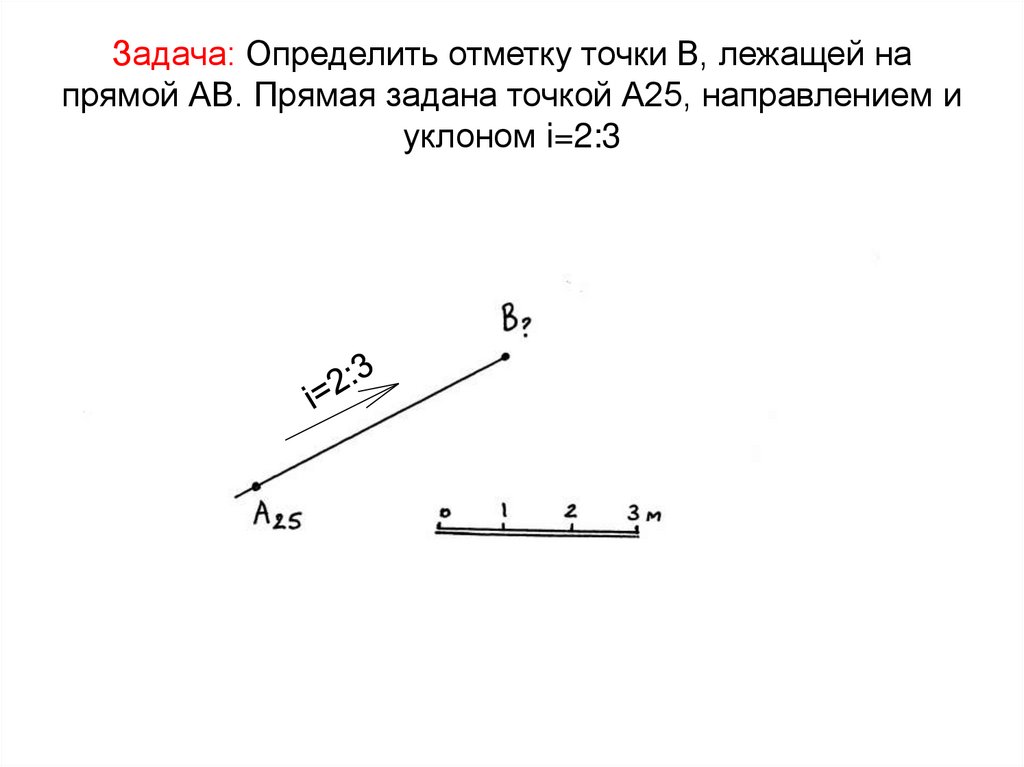
16. Задача: Определить отметку точки В, лежащей на прямой АВ. Прямая задана точкой А25, направлением и уклоном i=2:3
17. Решение: 1.Определяем величину интервала прямой
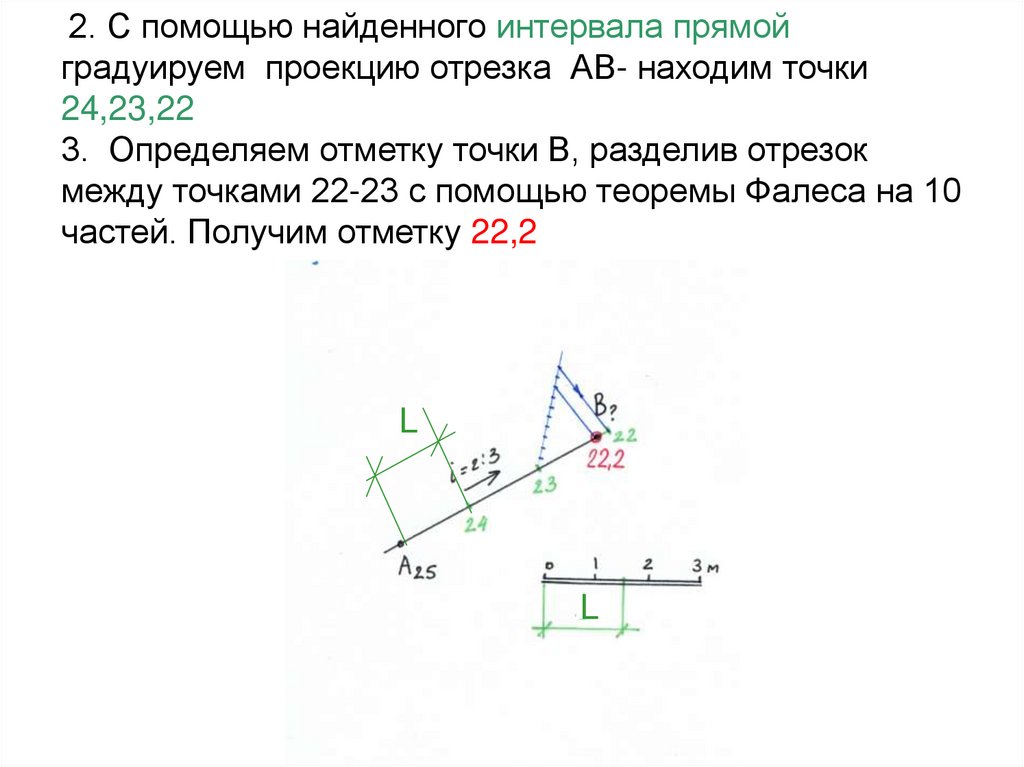
18. 2. С помощью найденного интервала прямой градуируем проекцию отрезка АВ- находим точки 24,23,22 3. Определяем отметку точки В,
разделив отрезокмежду точками 22-23 с помощью теоремы Фалеса на 10
частей. Получим отметку 22,2
L
L
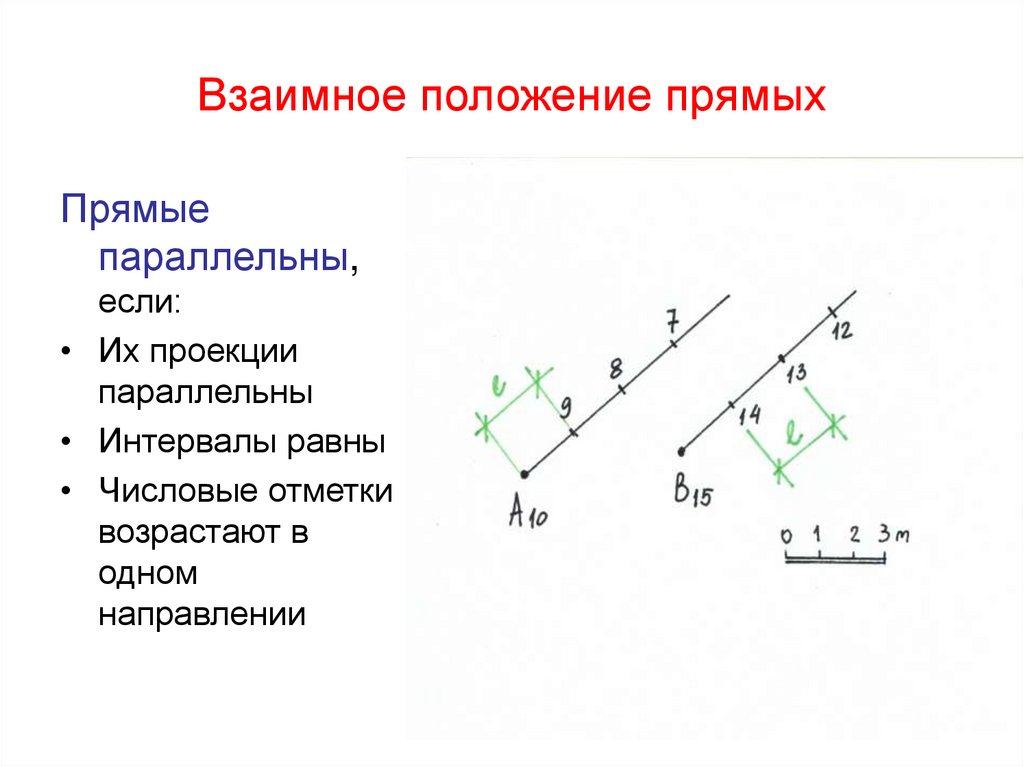
19. Взаимное положение прямых
Прямыепараллельны,
если:
• Их проекции
параллельны
• Интервалы равны
• Числовые отметки
возрастают в
одном
направлении
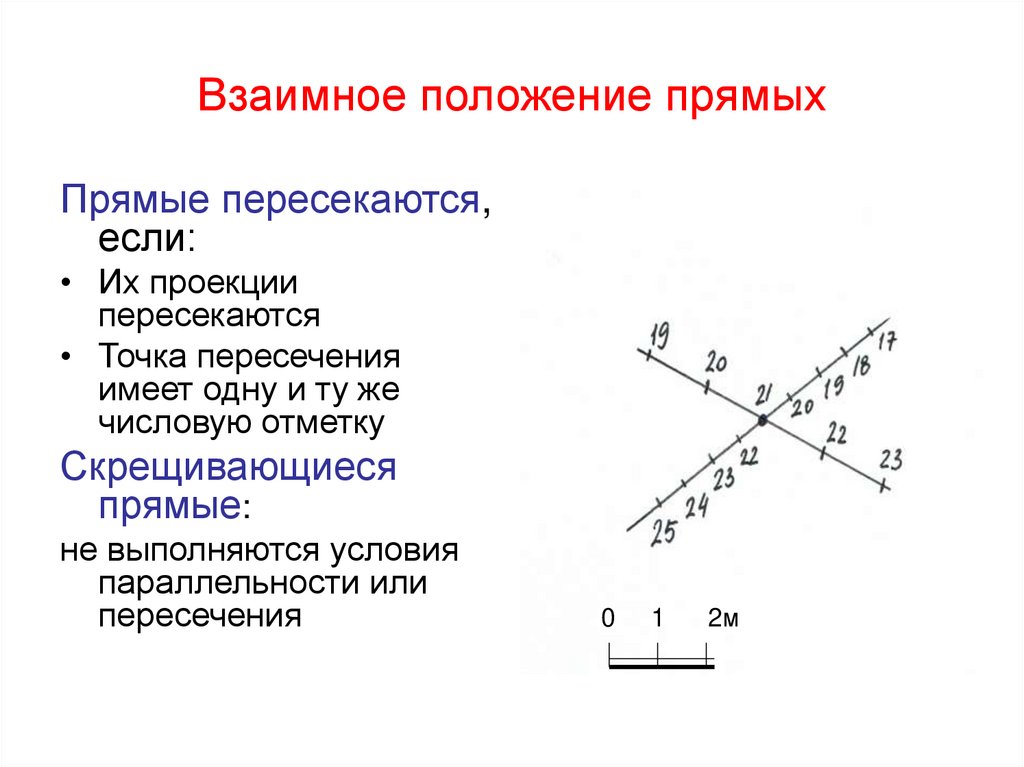
20. Взаимное положение прямых
Прямые пересекаются,если:
• Их проекции
пересекаются
• Точка пересечения
имеет одну и ту же
числовую отметку
Скрещивающиеся
прямые:
не выполняются условия
параллельности или
пересечения
0
1
2м
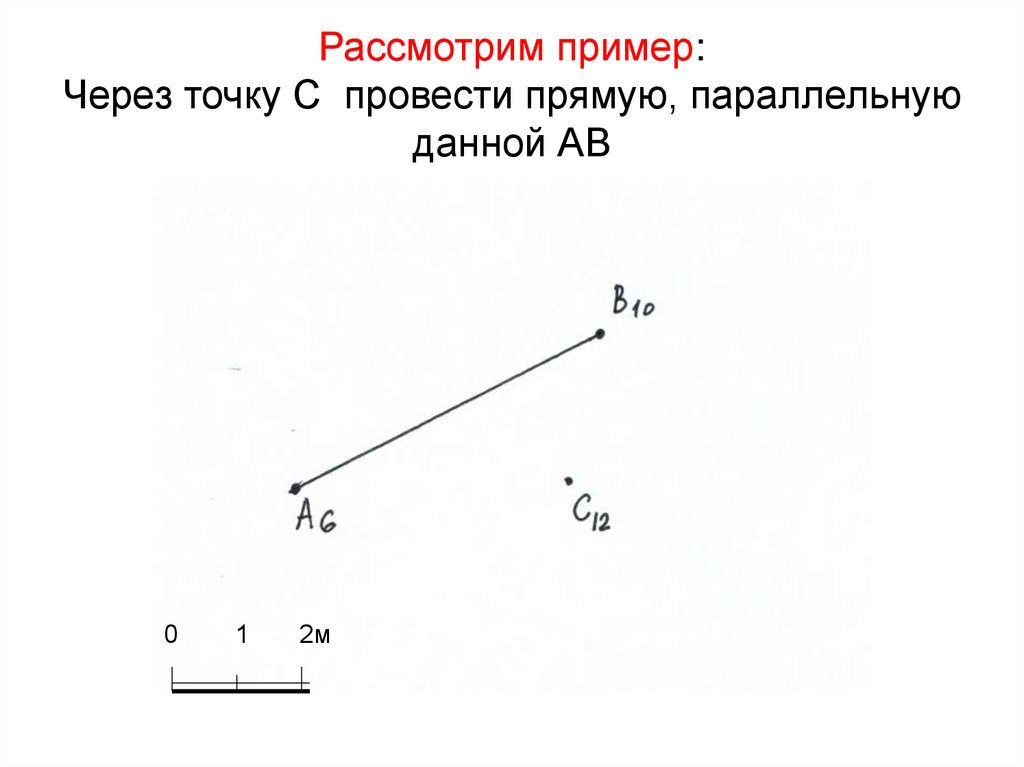
21. Рассмотрим пример: Через точку С провести прямую, параллельную данной АВ
01
2м
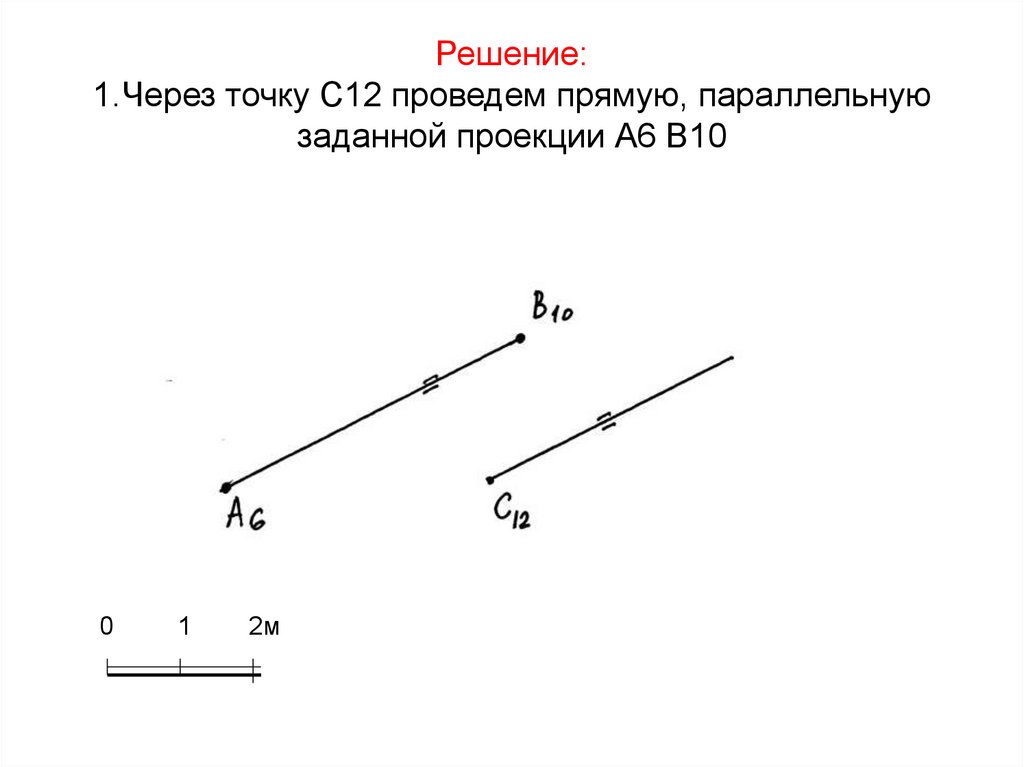
22. Решение: 1.Через точку С12 проведем прямую, параллельную заданной проекции А6 В10
01
2м
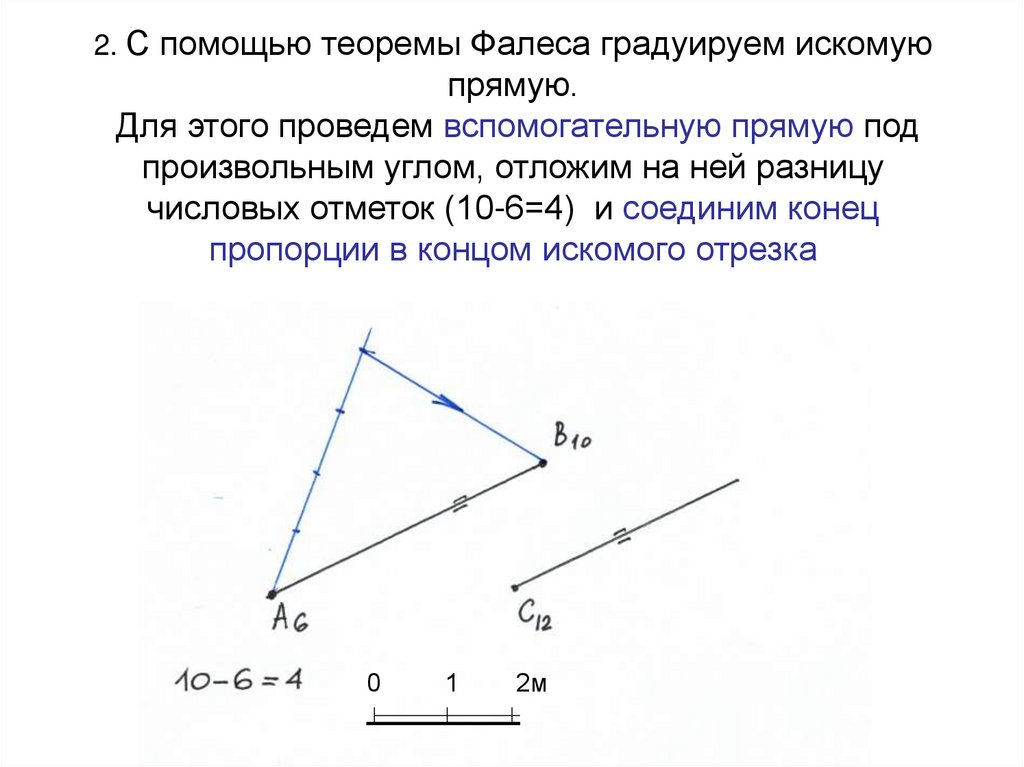
23. 2. С помощью теоремы Фалеса градуируем искомую прямую. Для этого проведем вспомогательную прямую под произвольным углом,
отложим на ней разницучисловых отметок (10-6=4) и соединим конец
пропорции в концом искомого отрезка
0
1
2м
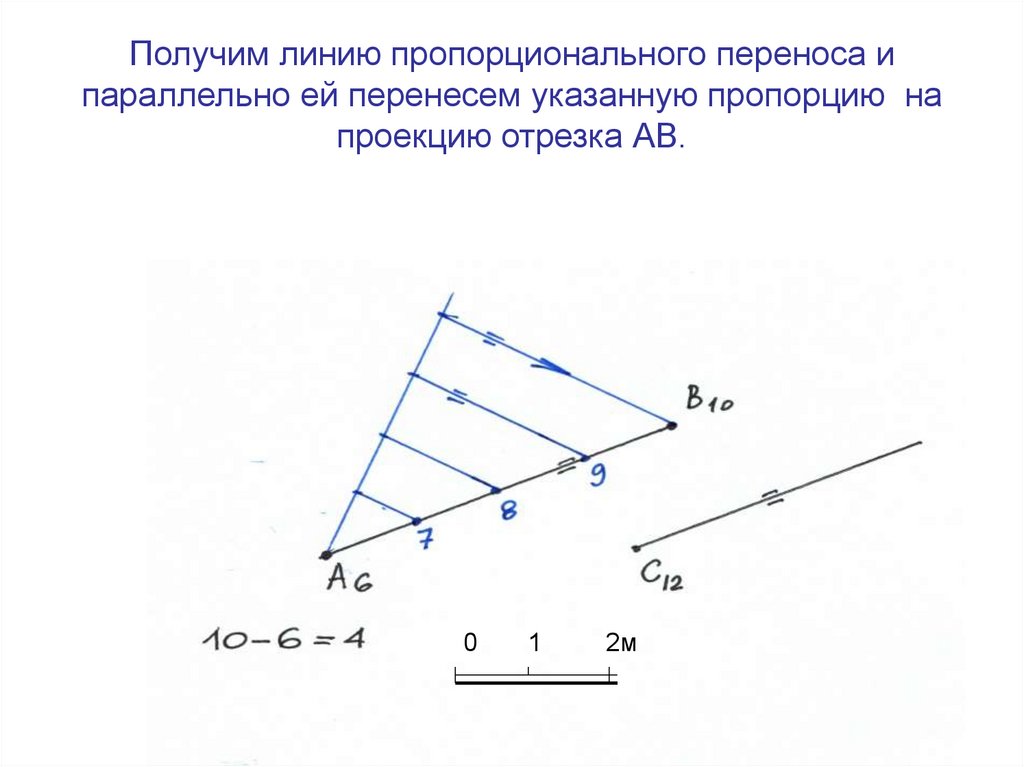
24. Получим линию пропорционального переноса и параллельно ей перенесем указанную пропорцию на проекцию отрезка АВ.
01
2м
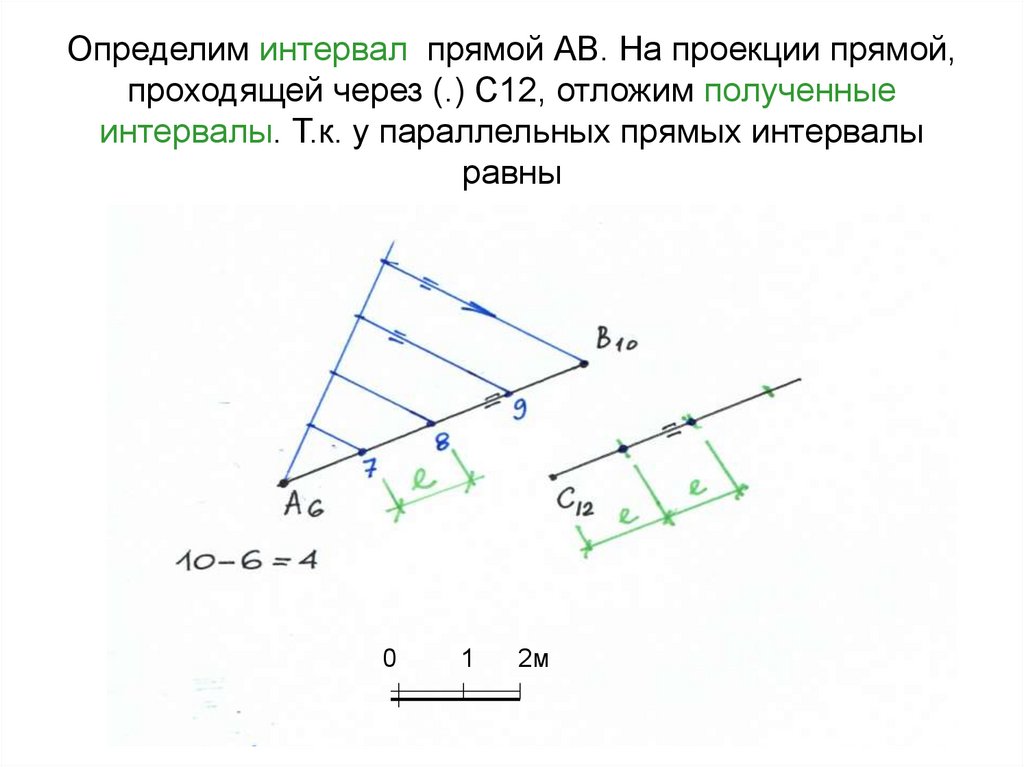
25. Определим интервал прямой АВ. На проекции прямой, проходящей через (.) С12, отложим полученные интервалы. Т.к. у параллельных
прямых интервалыравны
0
1
2м
26. 3. Числовые отметки возрастают в одном направлении- проставим отметки на прямой, проходящей через (.) С12 : 13,14,15
3. Числовые отметки возрастают в одном направлениипроставим отметки на прямой, проходящей через(.) С12 : 13,14,15
0
1
2м
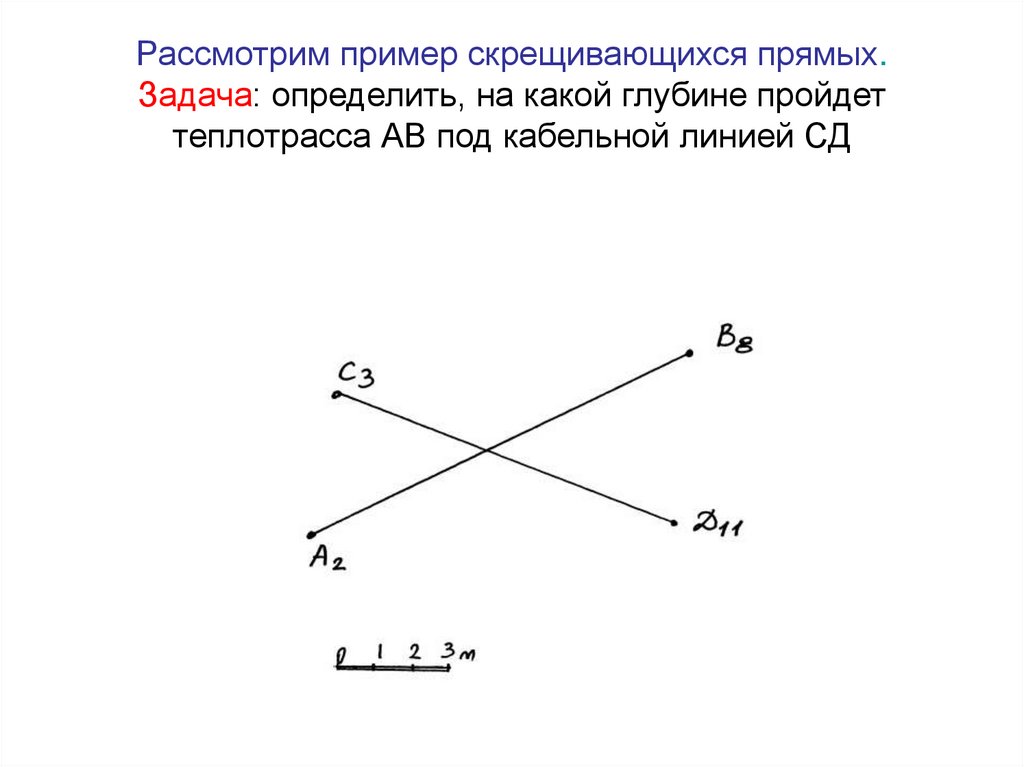
27. Рассмотрим пример скрещивающихся прямых. Задача: определить, на какой глубине пройдет теплотрасса АВ под кабельной линией СД
28. Проградуируем прямую СД. 1.определим разницу отметок концов отрезка 11-3=8. 2.через конец отрезка (.)С3 проведем произвольную
вспомогательнуюпрямую, на которой отложим 8 любых равных между собой отрезков,
последнюю точку пропорции соединим с концом отрезка (.)Д11- получим
линию пропорционального переноса
3. Перенесем полученную пропорцию с помощью параллельных прямых
на проекцию отрезка СД и проградуируем прямую СД
Вспомогательная
прямая
°
Линия пропорционального
переноса
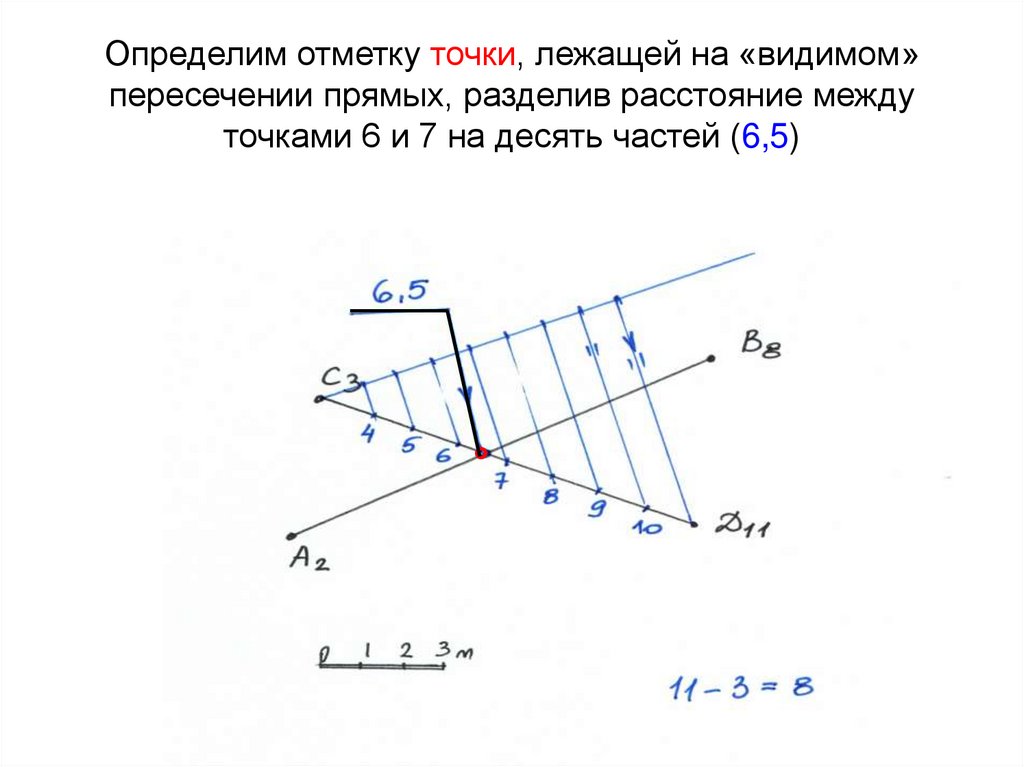
29. Определим отметку точки, лежащей на «видимом» пересечении прямых, разделив расстояние между точками 6 и 7 на десять частей
(6,5)°
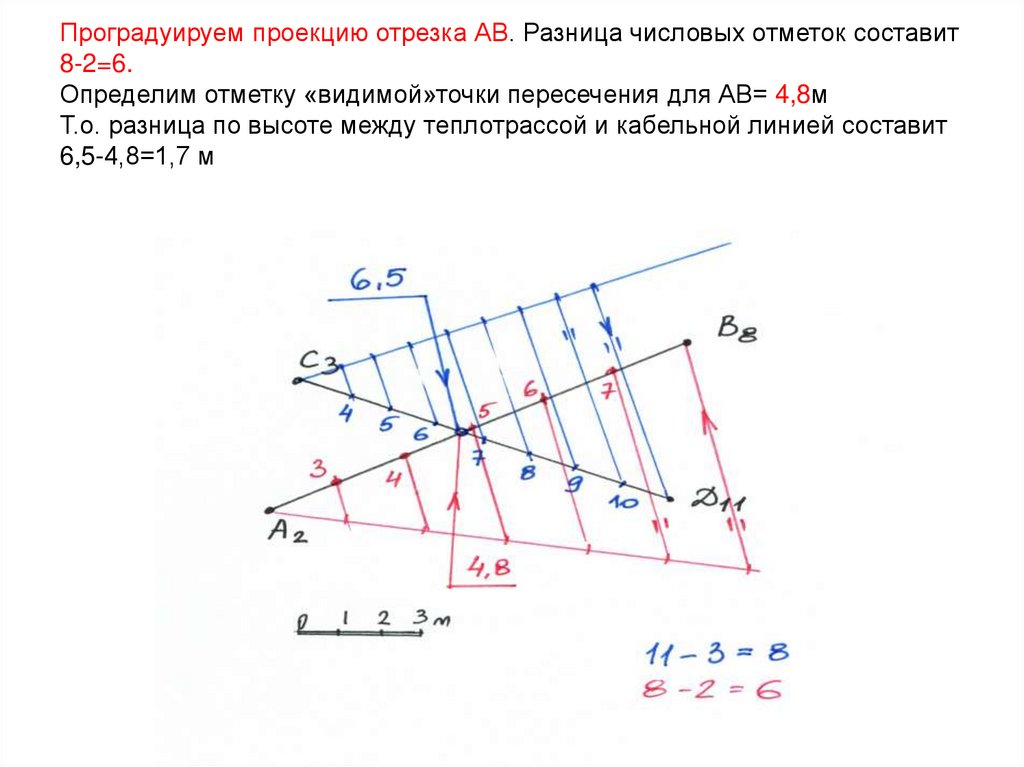
30. Проградуируем проекцию отрезка АВ. Разница числовых отметок составит 8-2=6. Определим отметку «видимой»точки пересечения для
АВ= 4,8мТ.о. разница по высоте между теплотрассой и кабельной линией составит
6,5-4,8=1,7 м
31. Проекции плоскостей
Плоскость в проекциях с числовыми отметкамиможет быть задана:
• Тремя точками с числовыми отметками
• Точкой и прямой
• Двумя параллельными прямыми
• Двумя пересекающимися прямыми
• Отсеком (фрагмент плоскости)
• Масштабом уклона плоскости
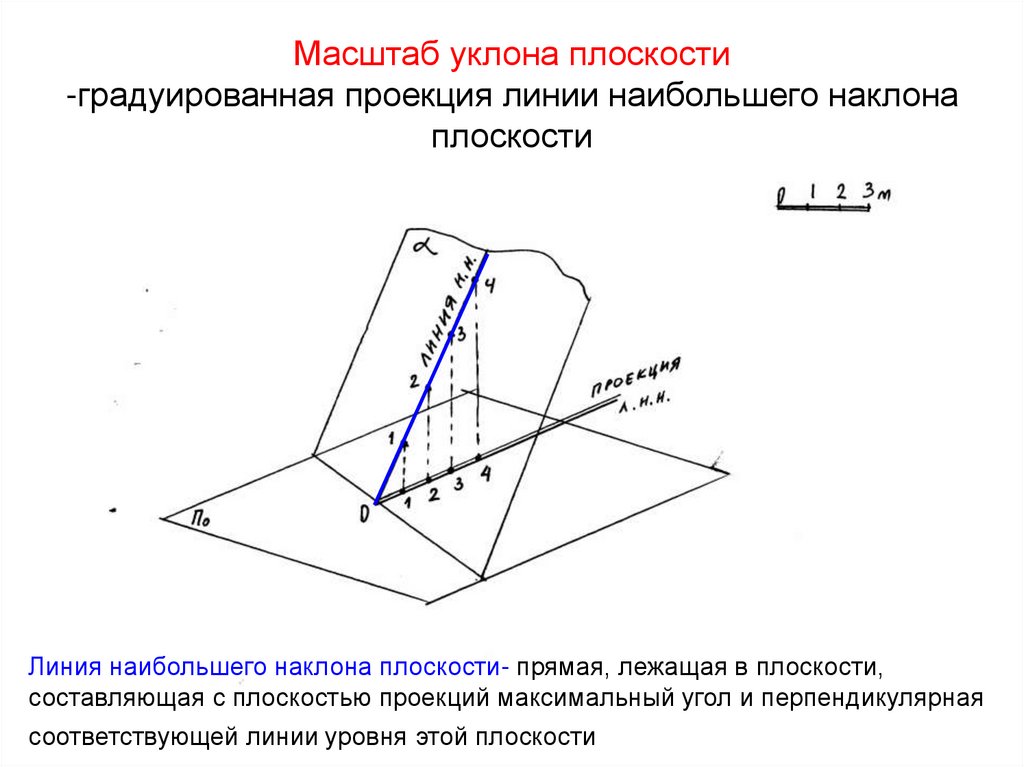
32. Масштаб уклона плоскости -градуированная проекция линии наибольшего наклона плоскости
Линия наибольшего наклона плоскости- прямая, лежащая в плоскости,составляющая с плоскостью проекций максимальный угол и перпендикулярная
соответствующей линии уровня этой плоскости
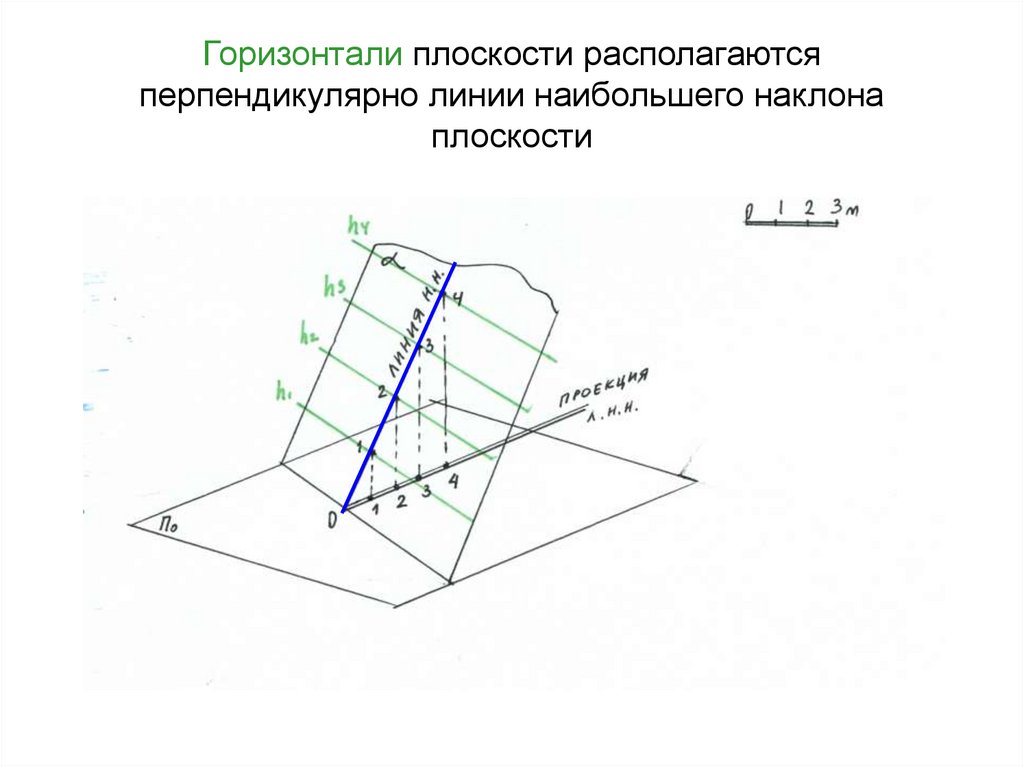
33. Горизонтали плоскости располагаются перпендикулярно линии наибольшего наклона плоскости
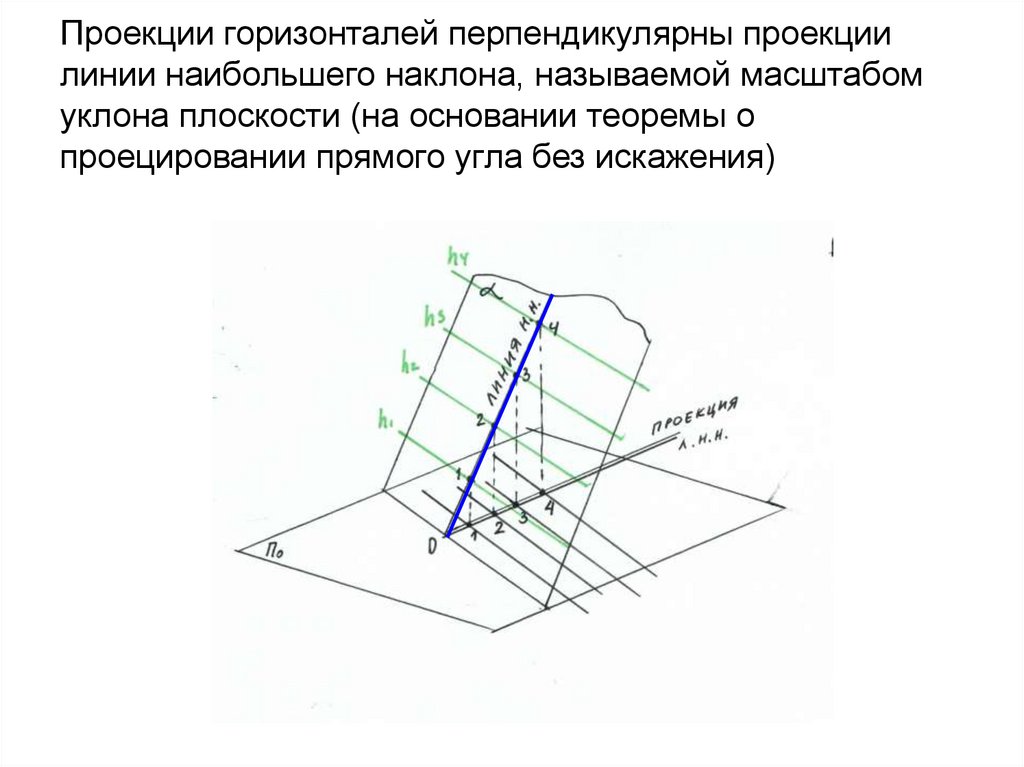
34. Проекции горизонталей перпендикулярны проекции линии наибольшего наклона, называемой масштабом уклона плоскости (на основании
теоремы опроецировании прямого угла без искажения)
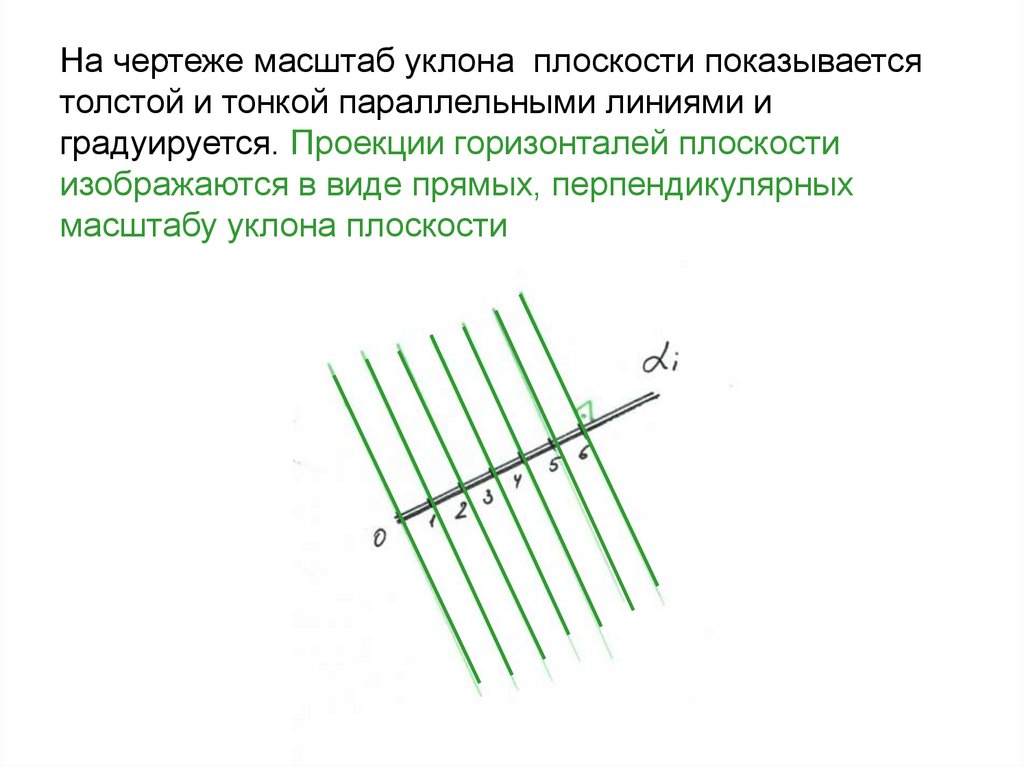
35. На чертеже масштаб уклона плоскости показывается толстой и тонкой параллельными линиями и градуируется. Проекции горизонталей
плоскостиизображаются в виде прямых, перпендикулярных
масштабу уклона плоскости
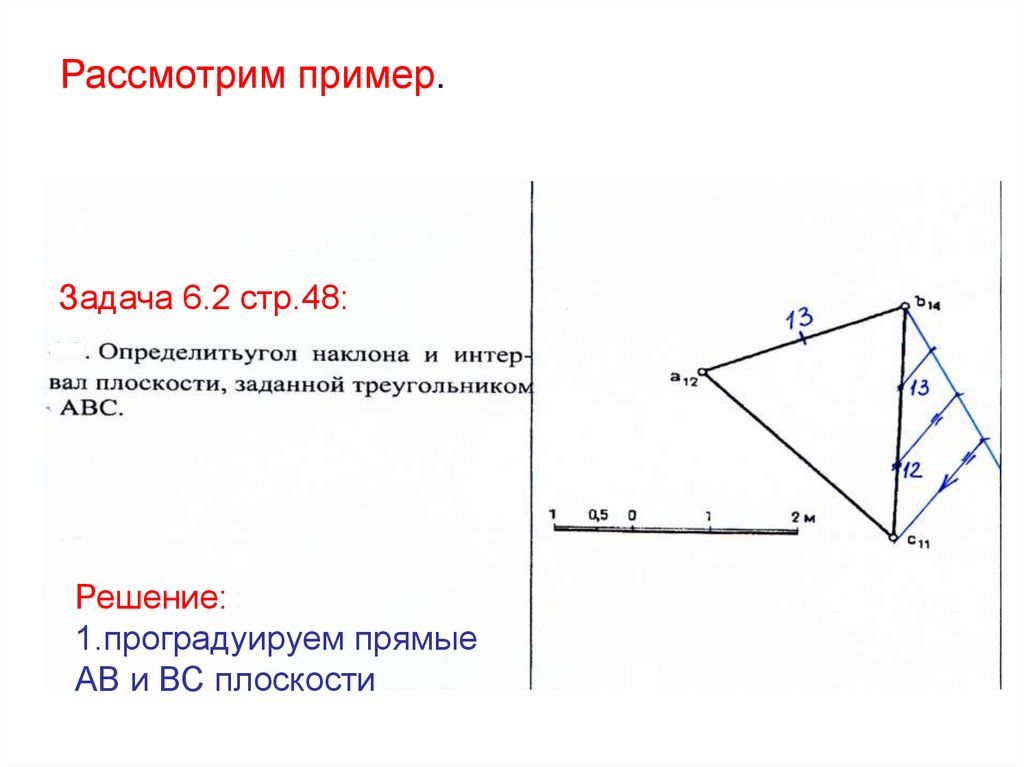
36. Рассмотрим пример.
Задача 6.2 стр.48:Решение:
1.проградуируем прямые
АВ и ВС плоскости
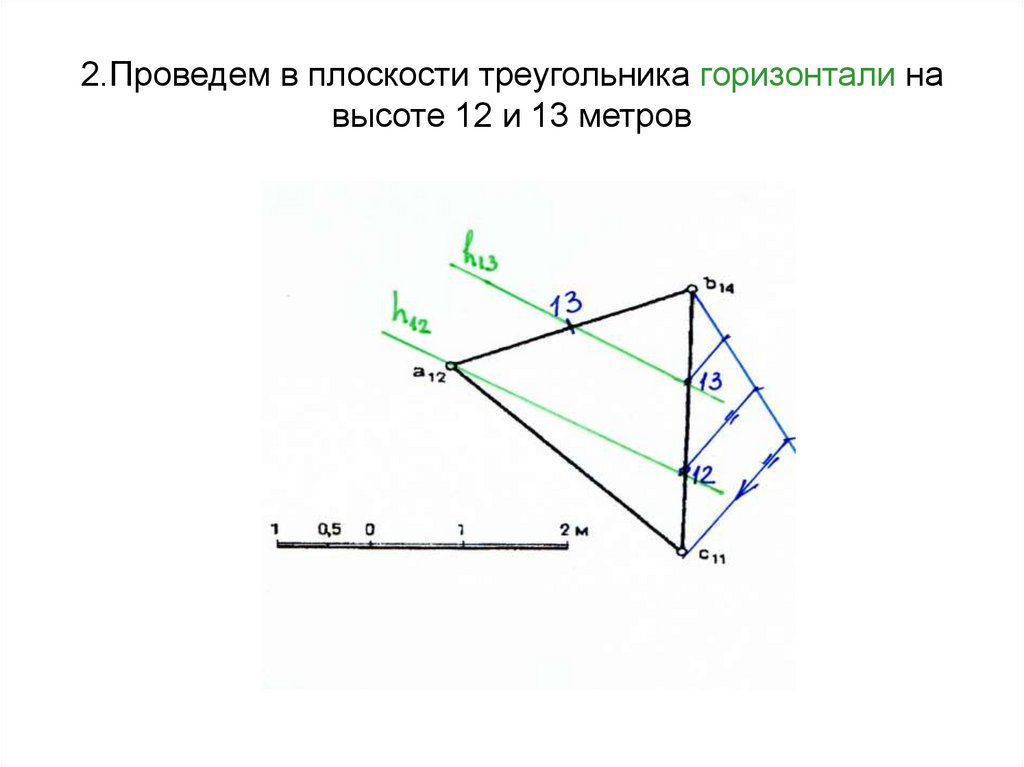
37. 2.Проведем в плоскости треугольника горизонтали на высоте 12 и 13 метров
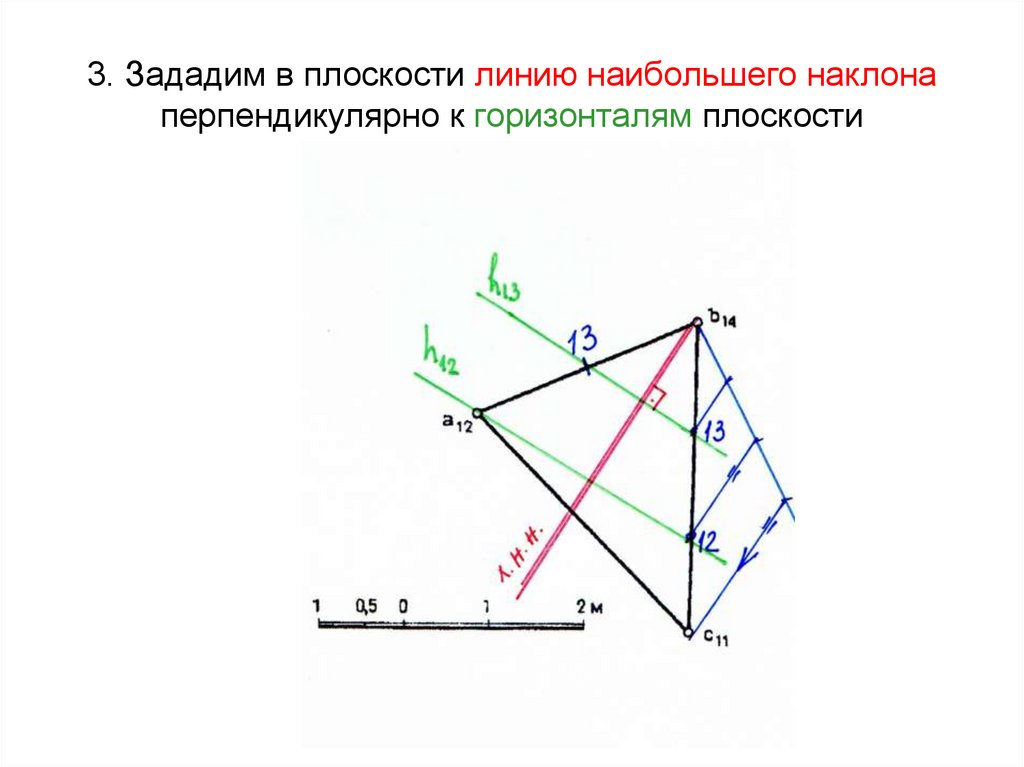
38. 3. Зададим в плоскости линию наибольшего наклона перпендикулярно к горизонталям плоскости
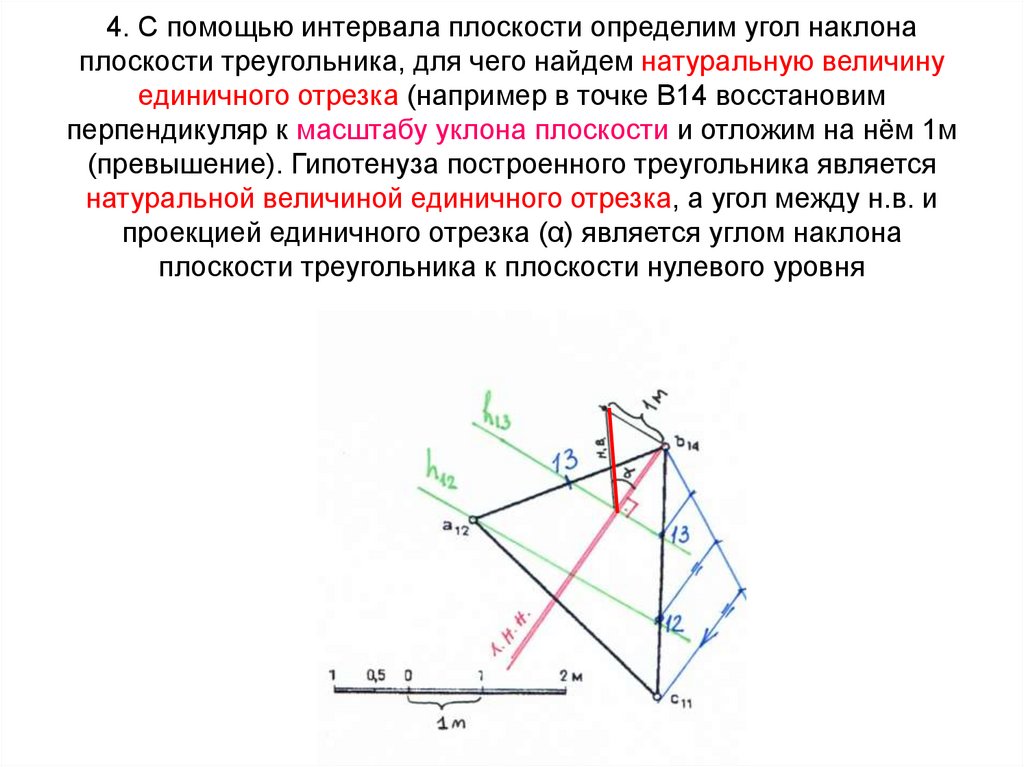
39. 4. С помощью интервала плоскости определим угол наклона плоскости треугольника, для чего найдем натуральную величину единичного
отрезка (например в точке В14 восстановимперпендикуляр к масштабу уклона плоскости и отложим на нём 1м
(превышение). Гипотенуза построенного треугольника является
натуральной величиной единичного отрезка, а угол между н.в. и
проекцией единичного отрезка (α) является углом наклона
плоскости треугольника к плоскости нулевого уровня
40. Взаимное расположение точки , прямой и плоскости
Точка принадлежит плоскости, если онапринадлежит прямой, лежащей в этой
плоскости.
Прямая принадлежит плоскости, если
она:
• проходит через две точки плоскости
• проходит через точку плоскости,
параллельно прямой, лежащей в этой
плоскости
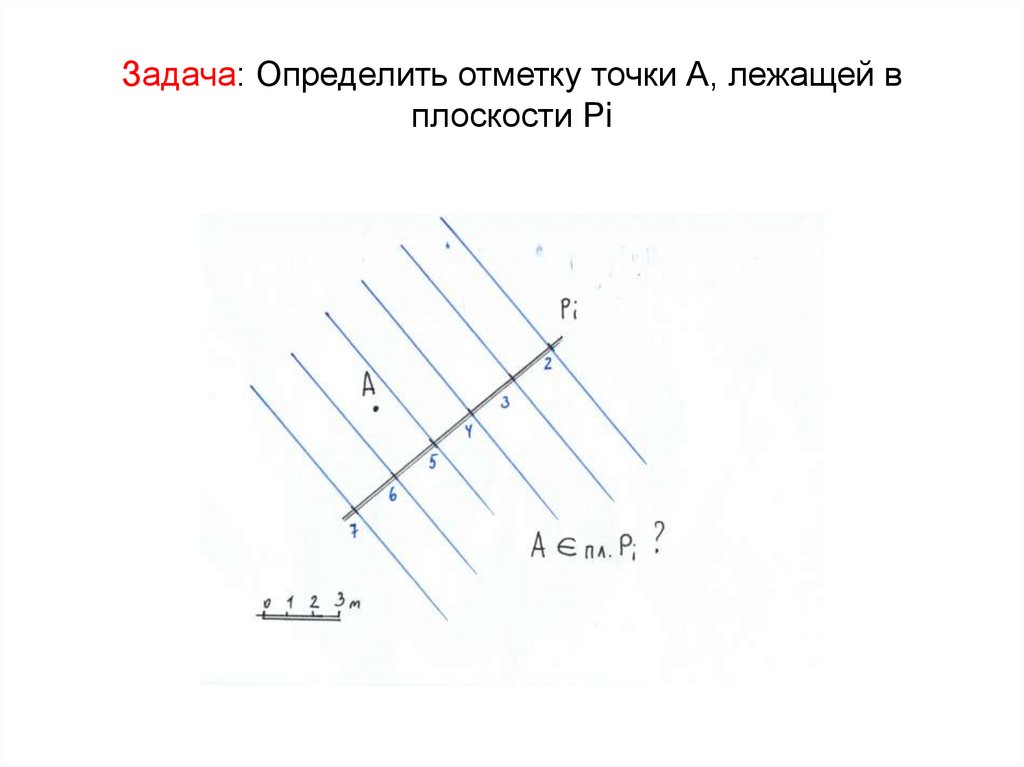
41. Задача: Определить отметку точки А, лежащей в плоскости Рi
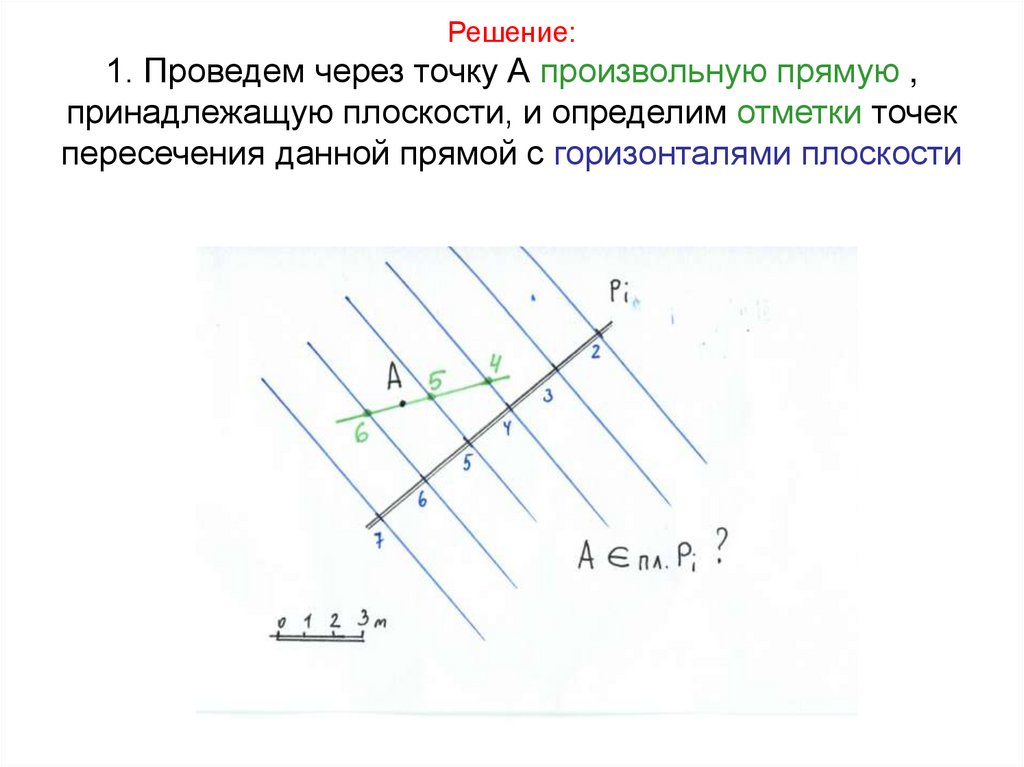
42. Решение: 1. Проведем через точку А произвольную прямую , принадлежащую плоскости, и определим отметки точек пересечения данной
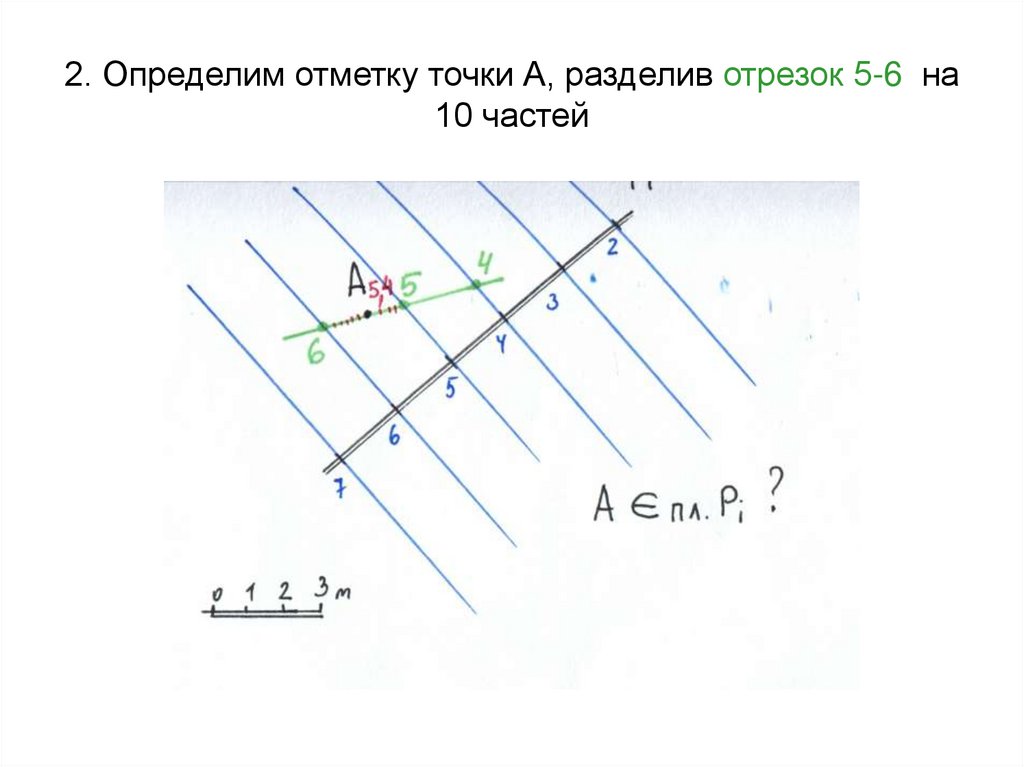
прямой с горизонталями плоскости43. 2. Определим отметку точки А, разделив отрезок 5-6 на 10 частей
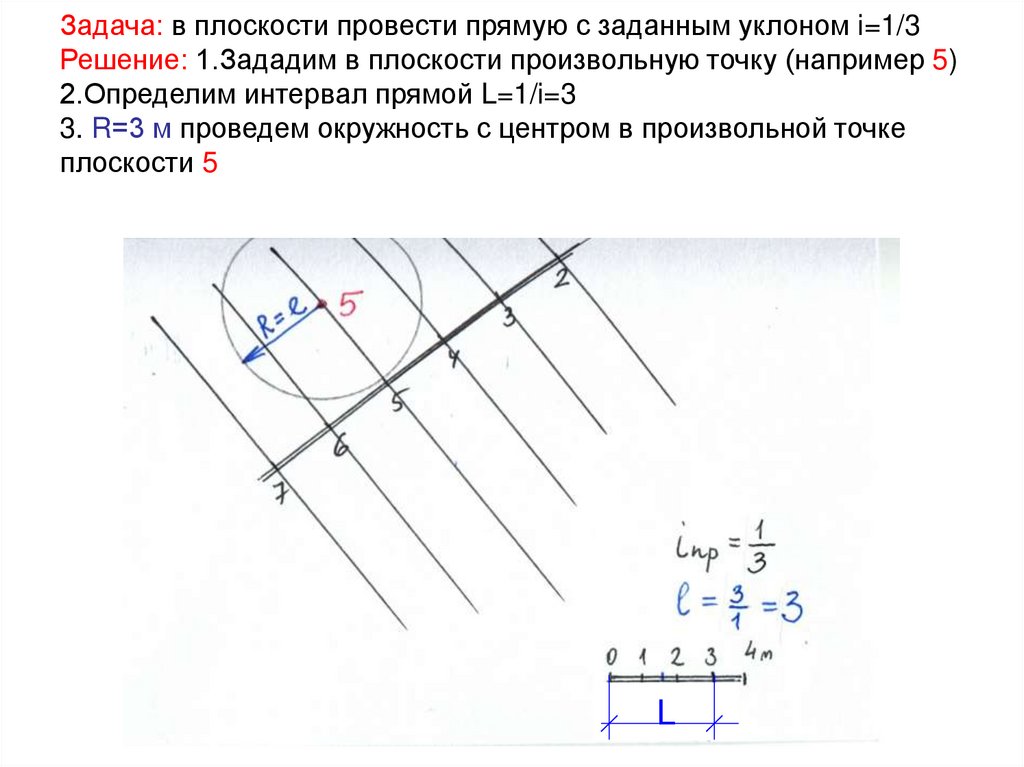
44. Задача: в плоскости провести прямую с заданным уклоном i=1/3 Решение: 1.Зададим в плоскости произвольную точку (например 5)
2.Определим интервал прямой L=1/i=33. R=3 м проведем окружность с центром в произвольной точке
плоскости 5
L
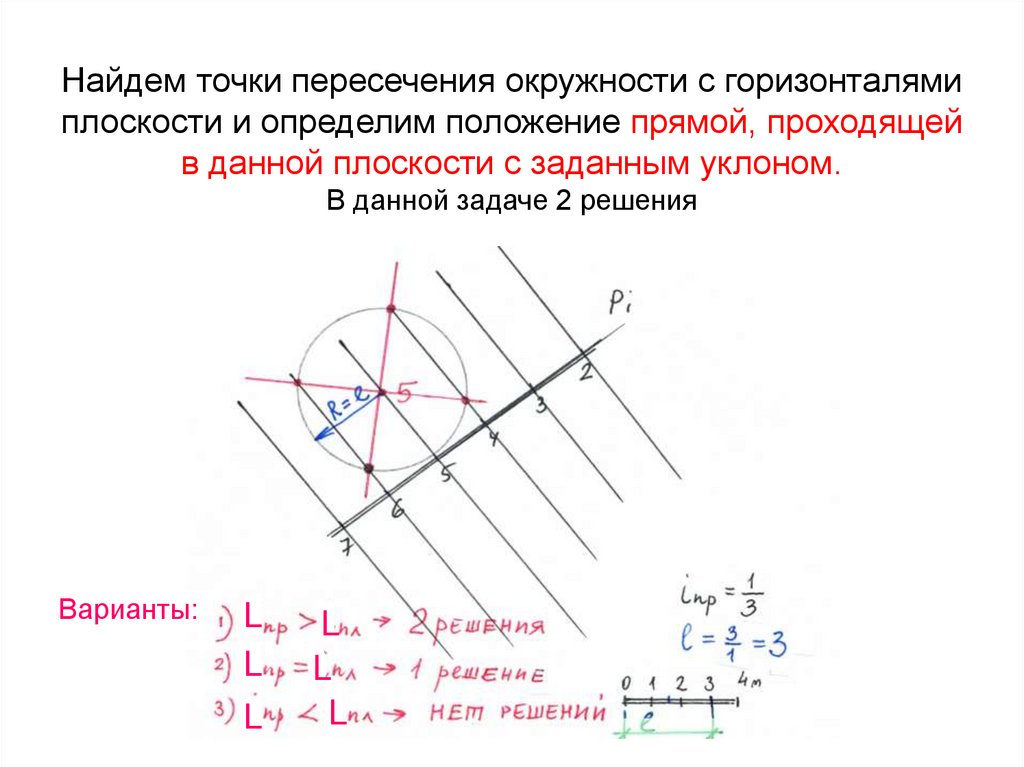
45. Найдем точки пересечения окружности с горизонталями плоскости и определим положение прямой, проходящей в данной плоскости с
заданным уклоном.В данной задаче 2 решения
Варианты:
L
L
L
L
L
L
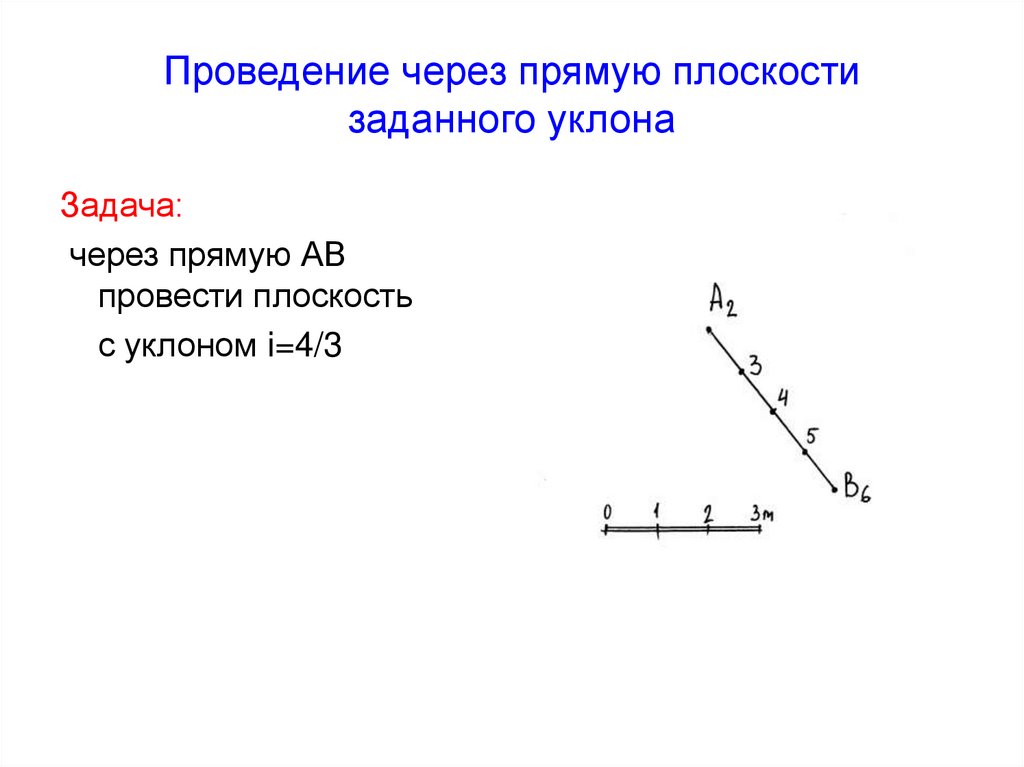
46. Проведение через прямую плоскости заданного уклона
Задача:через прямую АВ
провести плоскость
с уклоном i=4/3
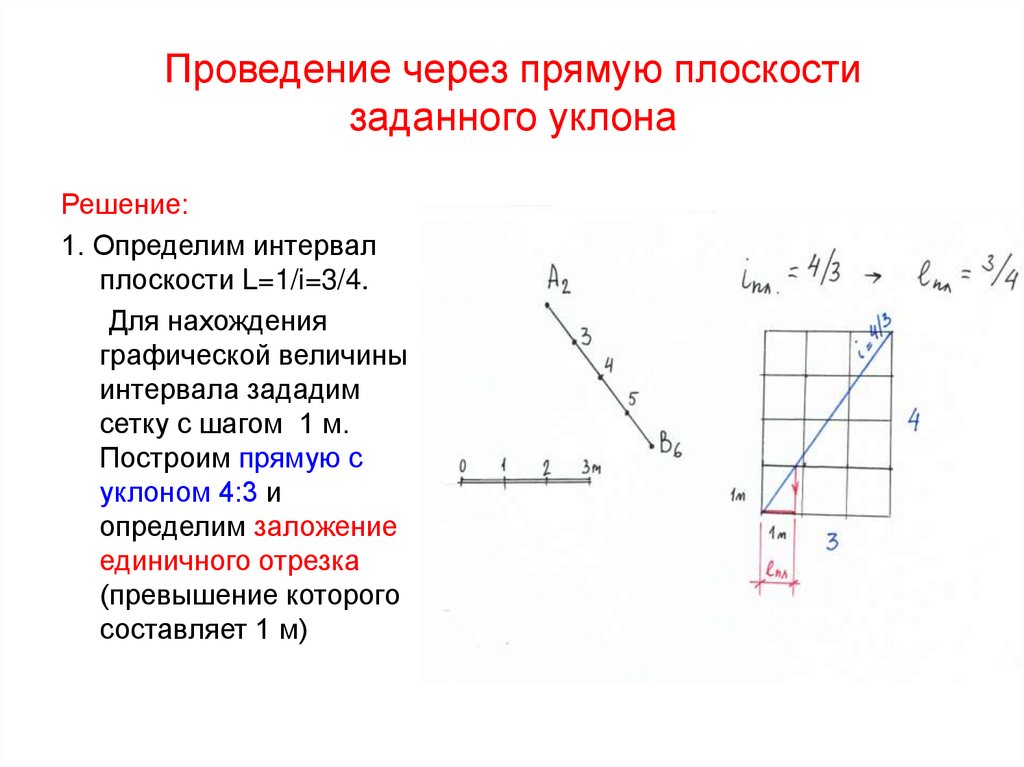
47. Проведение через прямую плоскости заданного уклона
Решение:1. Определим интервал
плоскости L=1/i=3/4.
Для нахождения
графической величины
интервала зададим
сетку с шагом 1 м.
Построим прямую с
уклоном 4:3 и
определим заложение
единичного отрезка
(превышение которого
составляет 1 м)
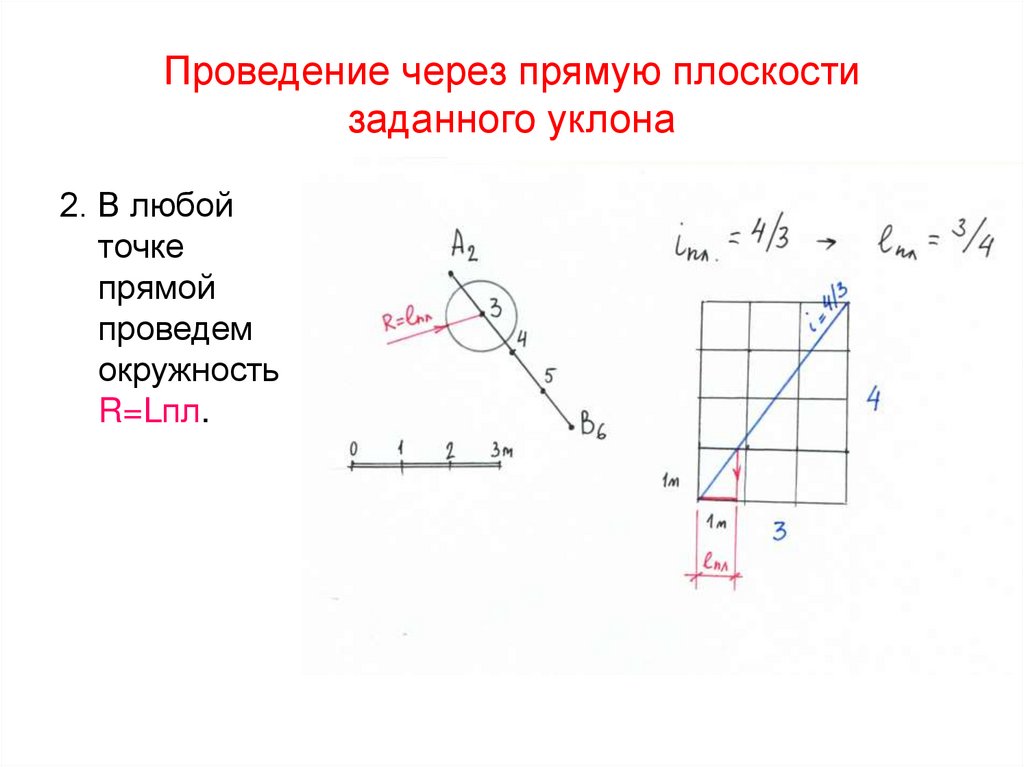
48. Проведение через прямую плоскости заданного уклона
2. В любойточке
прямой
проведем
окружность
R=Lпл.
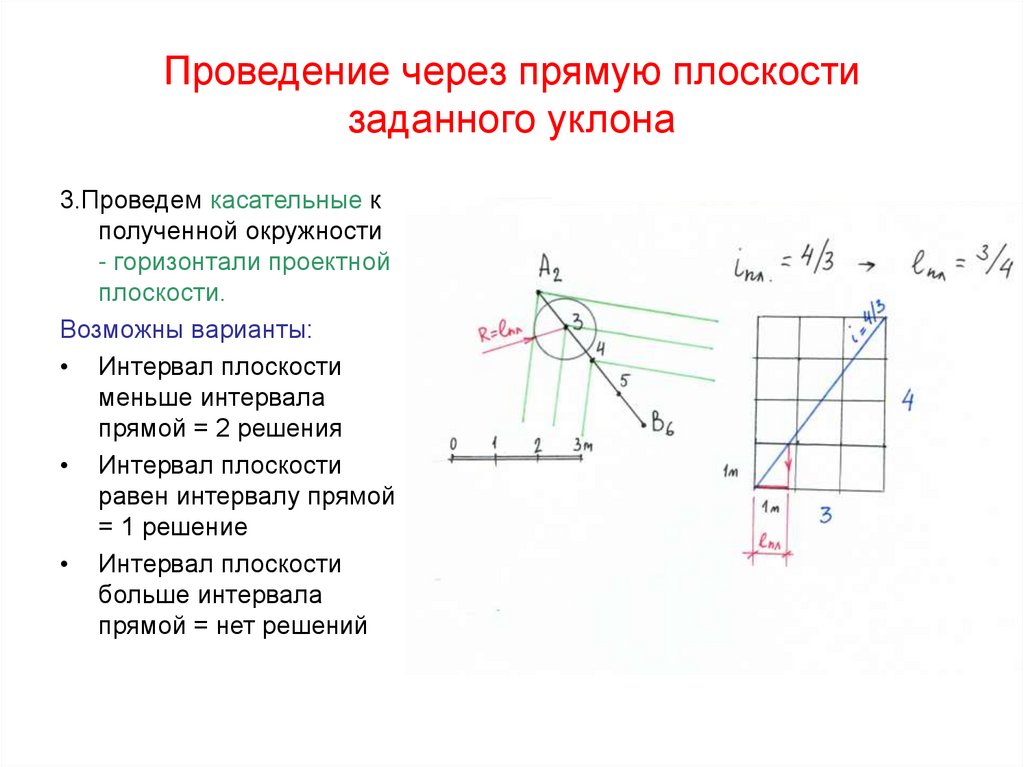
49. Проведение через прямую плоскости заданного уклона
3.Проведем касательные кполученной окружности
- горизонтали проектной
плоскости.
Возможны варианты:
• Интервал плоскости
меньше интервала
прямой = 2 решения
• Интервал плоскости
равен интервалу прямой
= 1 решение
• Интервал плоскости
больше интервала
прямой = нет решений
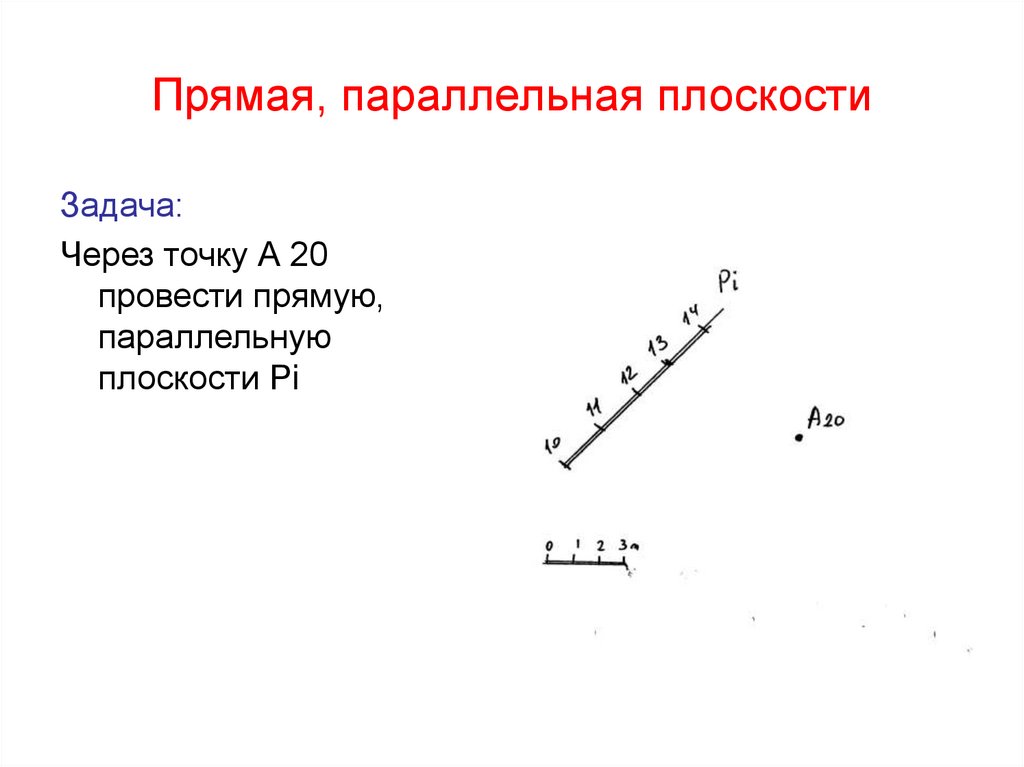
50. Прямая, параллельная плоскости
Задача:Через точку А 20
провести прямую,
параллельную
плоскости Рi
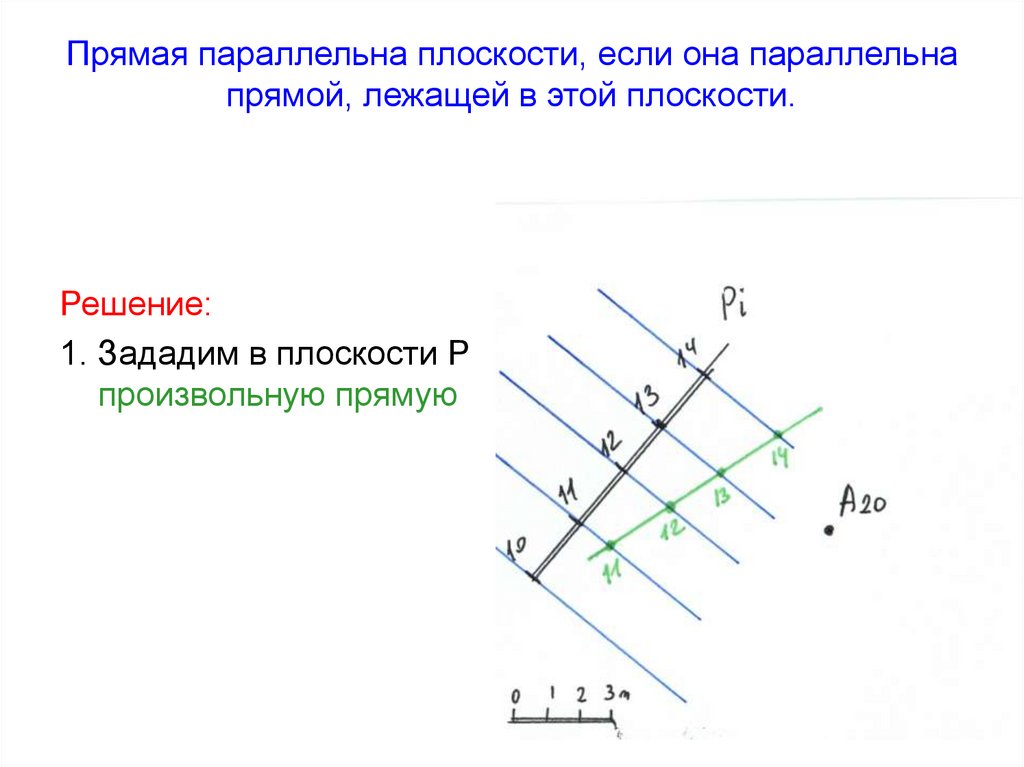
51. Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости.
Решение:1. Зададим в плоскости Р
произвольную прямую
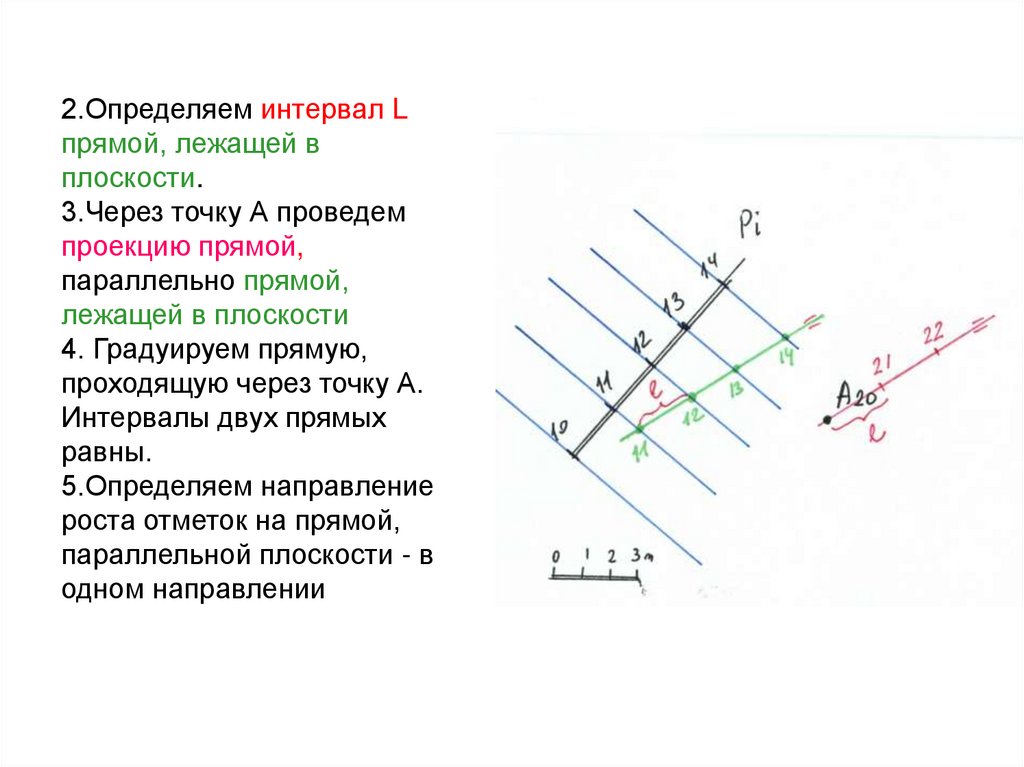
52. 2.Определяем интервал L прямой, лежащей в плоскости. 3.Через точку А проведем проекцию прямой, параллельно прямой, лежащей в
плоскости4. Градуируем прямую,
проходящую через точку А.
Интервалы двух прямых
равны.
5.Определяем направление
роста отметок на прямой,
параллельной плоскости - в
одном направлении
53. Пересечение прямой с плоскостью
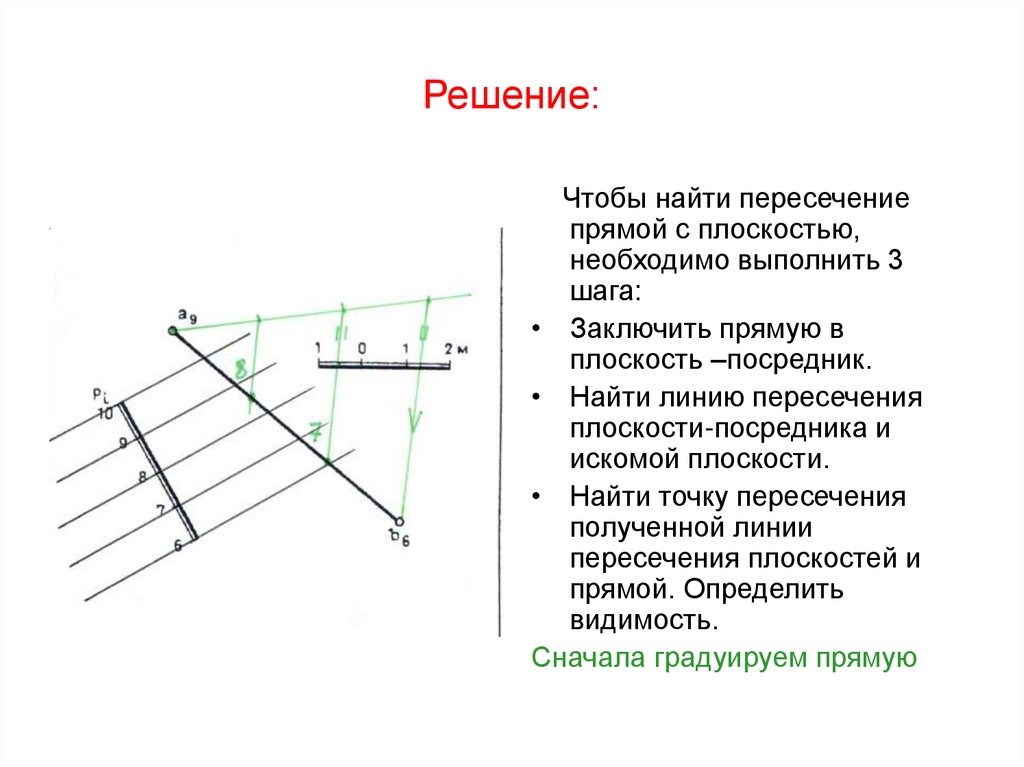
Задача 6.5 стр.49:54. Решение:
Чтобы найти пересечениепрямой с плоскостью,
необходимо выполнить 3
шага:
• Заключить прямую в
плоскость –посредник.
• Найти линию пересечения
плоскости-посредника и
искомой плоскости.
• Найти точку пересечения
полученной линии
пересечения плоскостей и
прямой. Определить
видимость.
Сначала градуируем прямую
55.
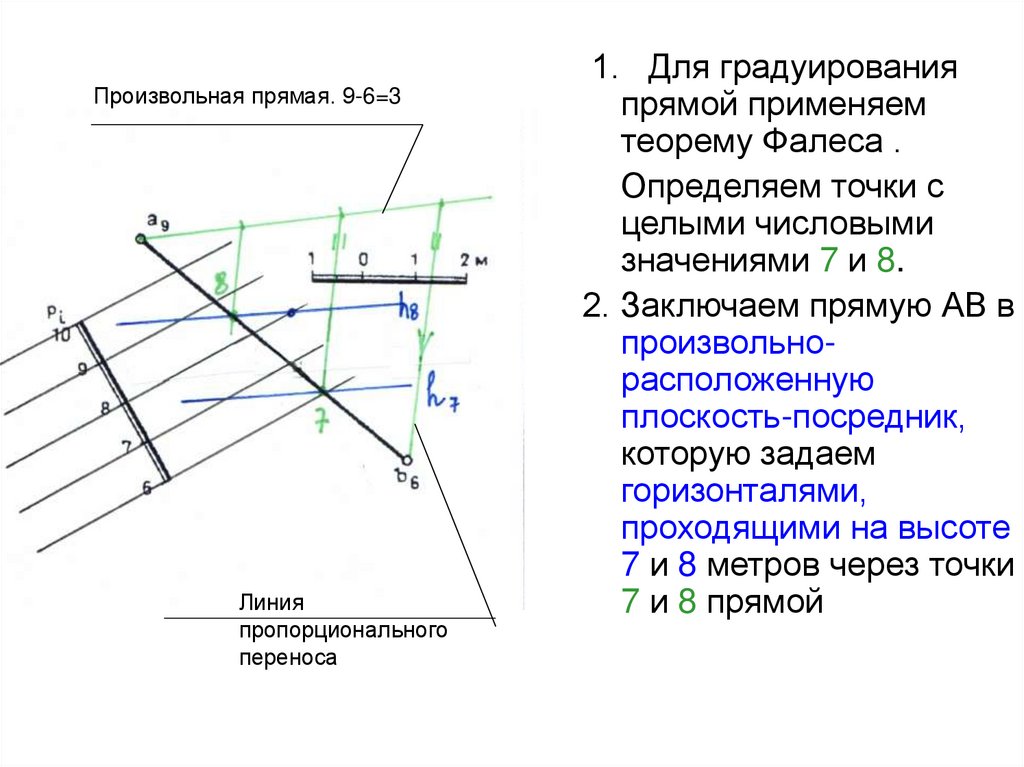
Произвольная прямая. 9-6=3Линия
пропорционального
переноса
1. Для градуирования
прямой применяем
теорему Фалеса .
Определяем точки с
целыми числовыми
значениями 7 и 8.
2. Заключаем прямую АВ в
произвольнорасположенную
плоскость-посредник,
которую задаем
горизонталями,
проходящими на высоте
7 и 8 метров через точки
7 и 8 прямой
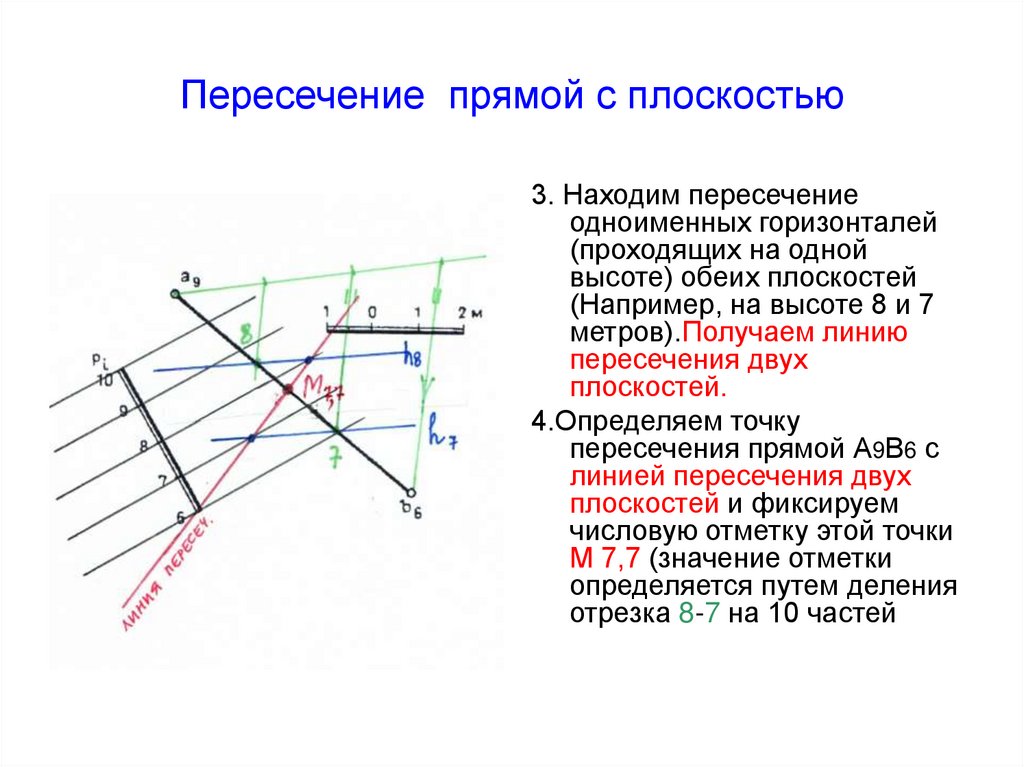
56. Пересечение прямой с плоскостью
3. Находим пересечениеодноименных горизонталей
(проходящих на одной
высоте) обеих плоскостей
(Например, на высоте 8 и 7
метров).Получаем линию
пересечения двух
плоскостей.
4.Определяем точку
пересечения прямой А9В6 с
линией пересечения двух
плоскостей и фиксируем
числовую отметку этой точки
М 7,7 (значение отметки
определяется путем деления
отрезка 8-7 на 10 частей
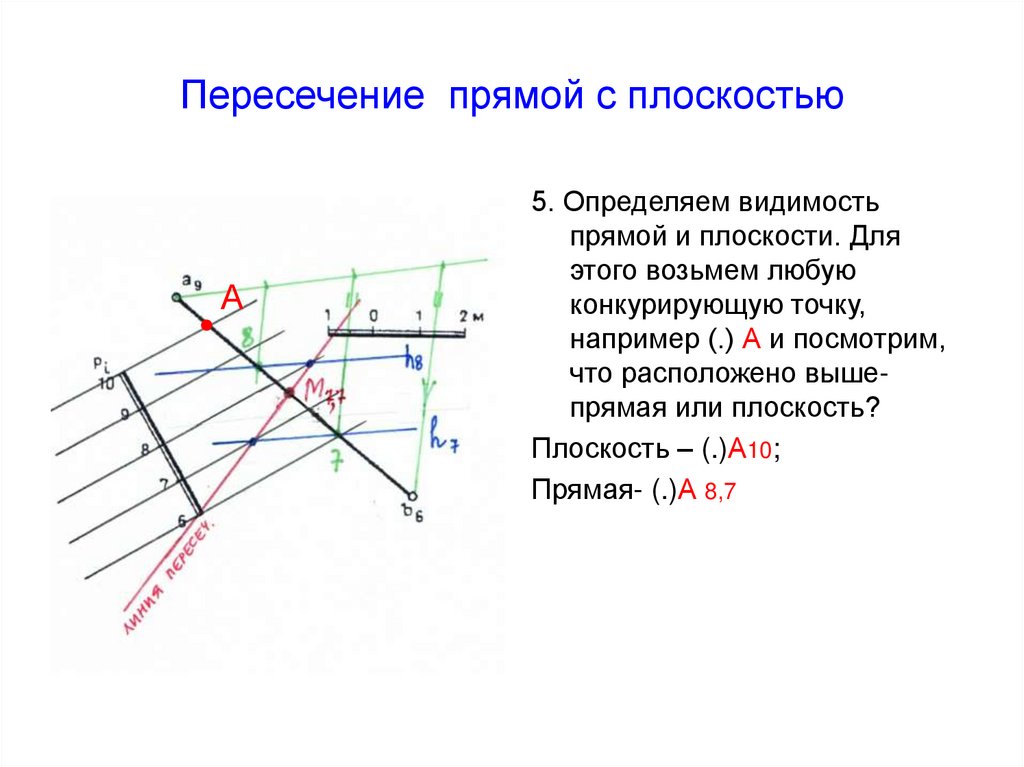
57. Пересечение прямой с плоскостью
А
5. Определяем видимость
прямой и плоскости. Для
этого возьмем любую
конкурирующую точку,
например (.) А и посмотрим,
что расположено вышепрямая или плоскость?
Плоскость – (.)А10;
Прямая- (.)А 8,7
58. Пересечение прямой с плоскостью
А
Вывод: Плоскость выше,
следовательно прямая не
видна
59. Взаимное расположение плоскостей
Две плоскости в пространстве могут быть взаимнопараллельными или пересекающимися.
Параллельные между собой плоскости имеют взаимно
параллельные масштабы уклона, с равными
интервалами и возрастанием (или убыванием)
отметок в одном направлении.
Если масштабы уклона заданных плоскостей не
удовлетворяют хотя бы одному условию взаимной
параллельности , то такие плоскости пересекаются
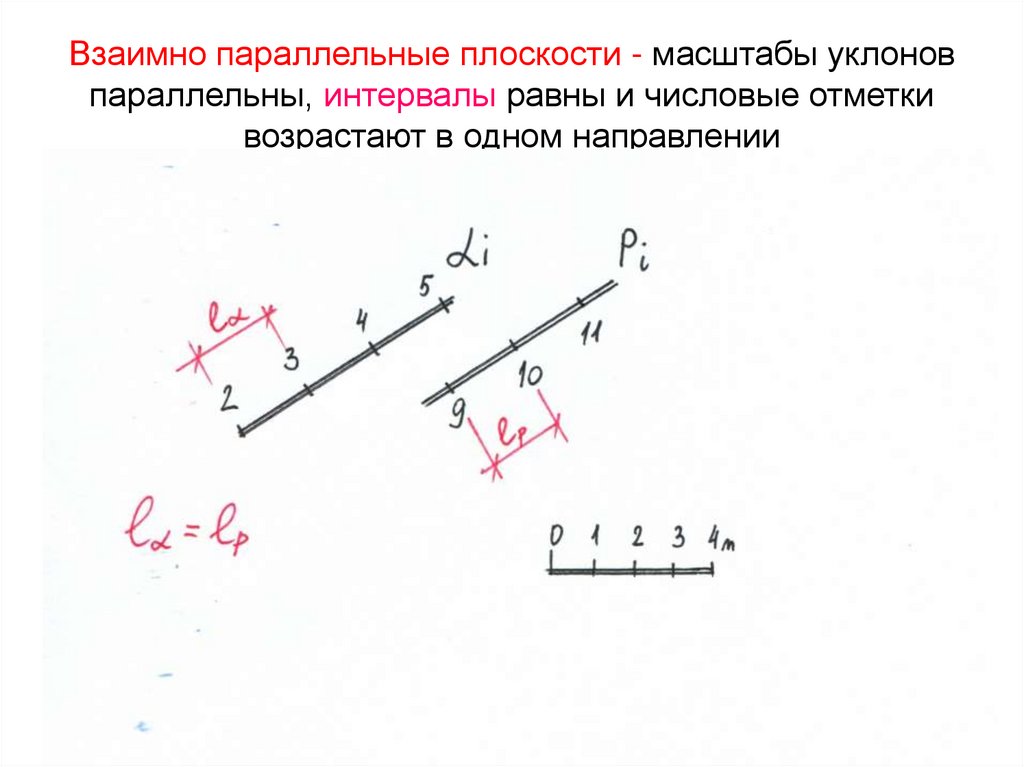
60. Взаимно параллельные плоскости - масштабы уклонов параллельны, интервалы равны и числовые отметки возрастают в одном
направлении61.
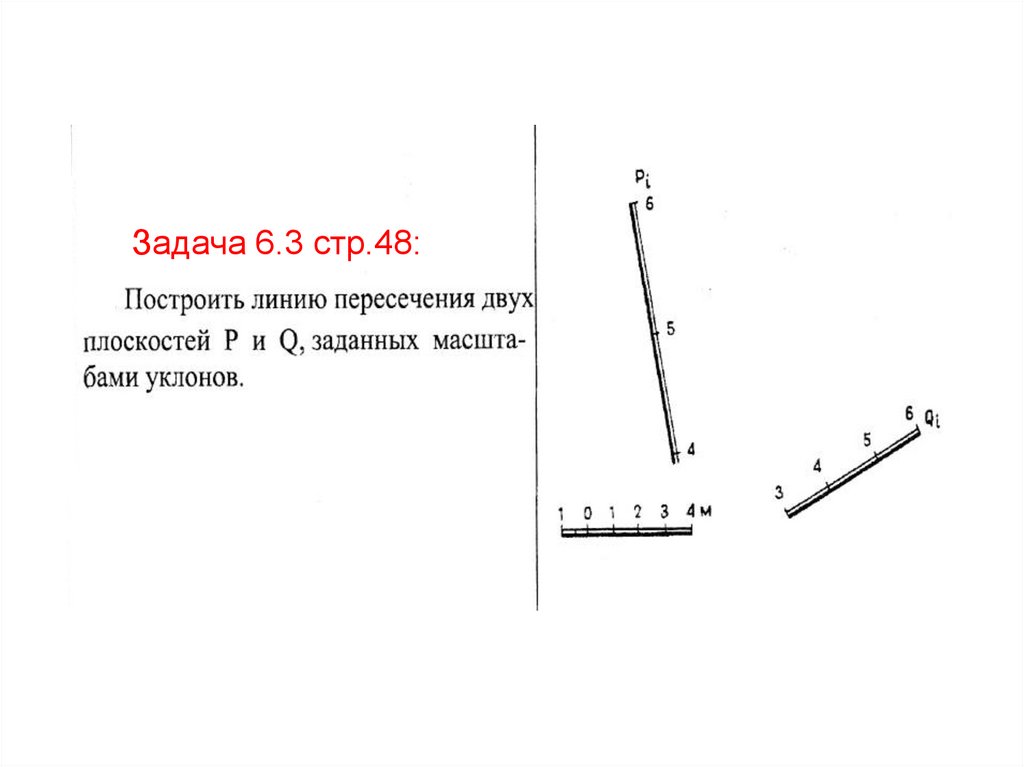
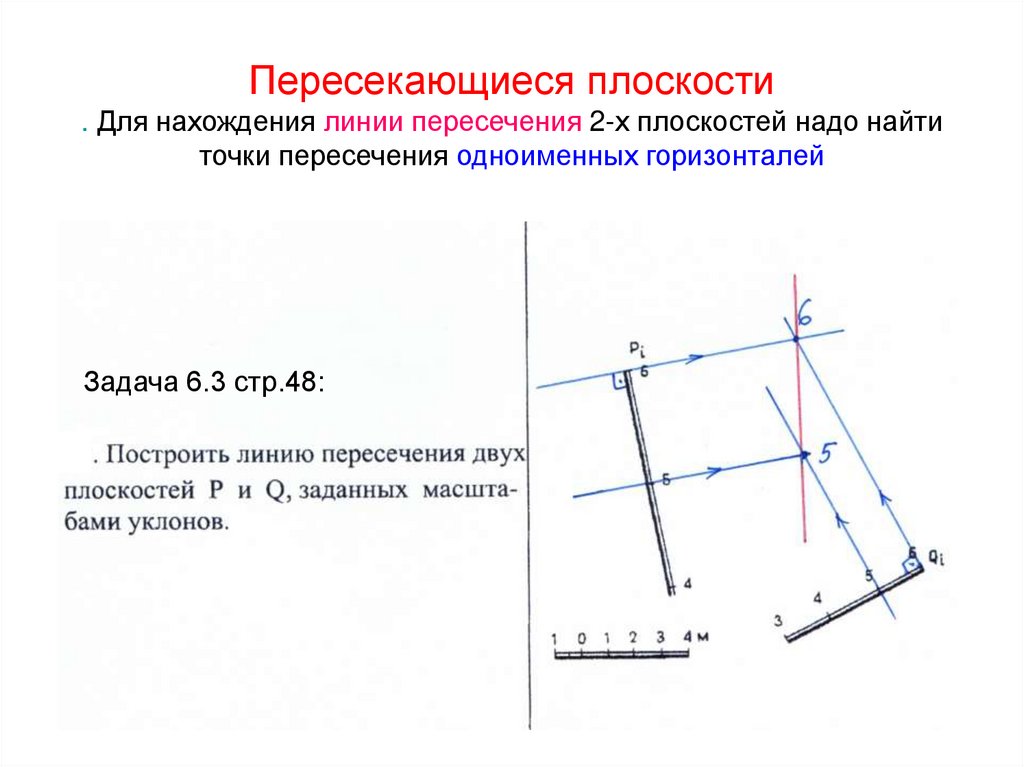
Задача 6.3 стр.48:62. Пересекающиеся плоскости . Для нахождения линии пересечения 2-х плоскостей надо найти точки пересечения одноименных
горизонталейЗадача 6.3 стр.48:
63. Поверхности
В проекциях с числовыми отметкамиповерхности задаются своими
горизонталями, получаемыми от мысленного
пересечения их горизонтальными
плоскостями, проводимыми на расстоянии
единицы масштаба (обычно 1 м) друг от
друга.
Если поверхность закономерная, ее
горизонтали имеют известную форму и
расположены в определенном порядке.
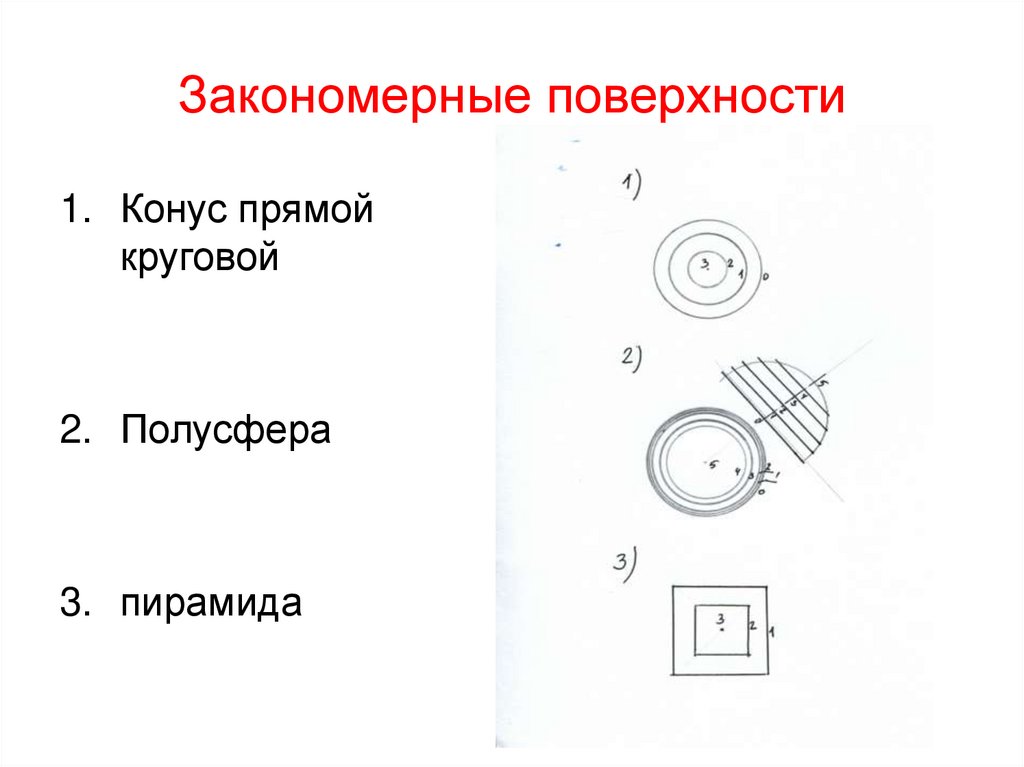
64. Закономерные поверхности
1. Конус прямойкруговой
2. Полусфера
3. пирамида
65. Графические поверхности
Незакономерныеповерхности называют
графическими.
Земная поверхность является
графической и называется
топографическая поверхность.
По горизонталям такой поверхности
можно судить о рельефе местности.
Расстояния между горизонталями
определяют уклон топографической
поверхности в том или ином
направлении. Если расстояние
между горизонталями уменьшается,
значит уклон данной поверхности
становится круче(больше) и
наоборот.
Например: а) холм, б) овраг
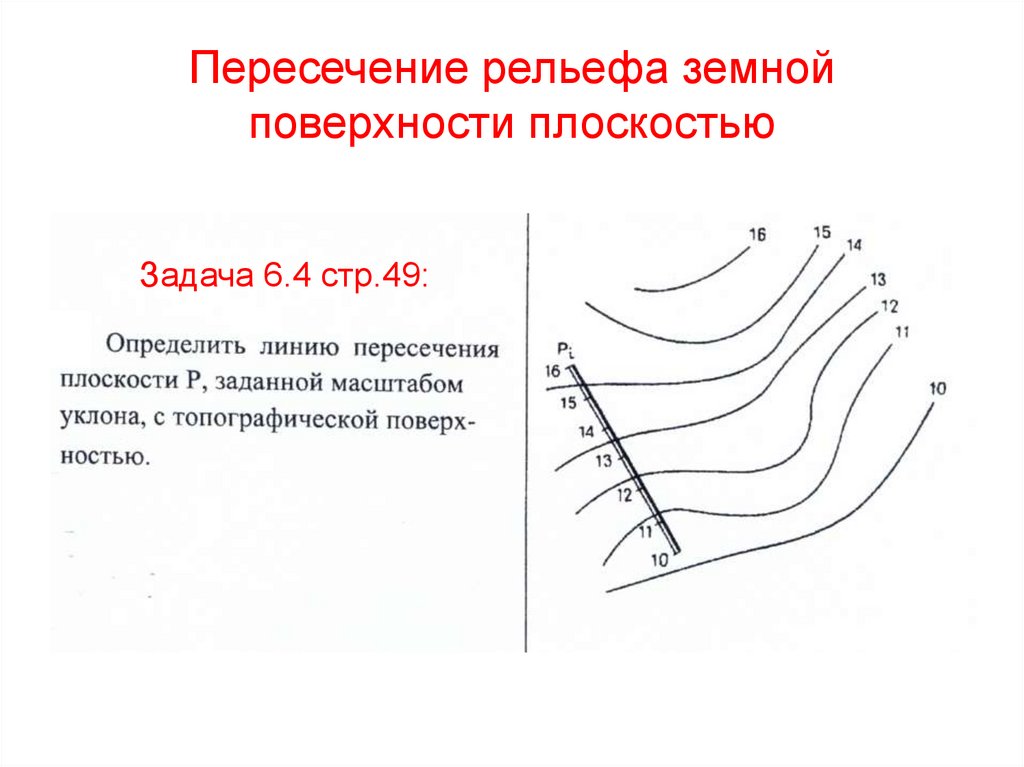
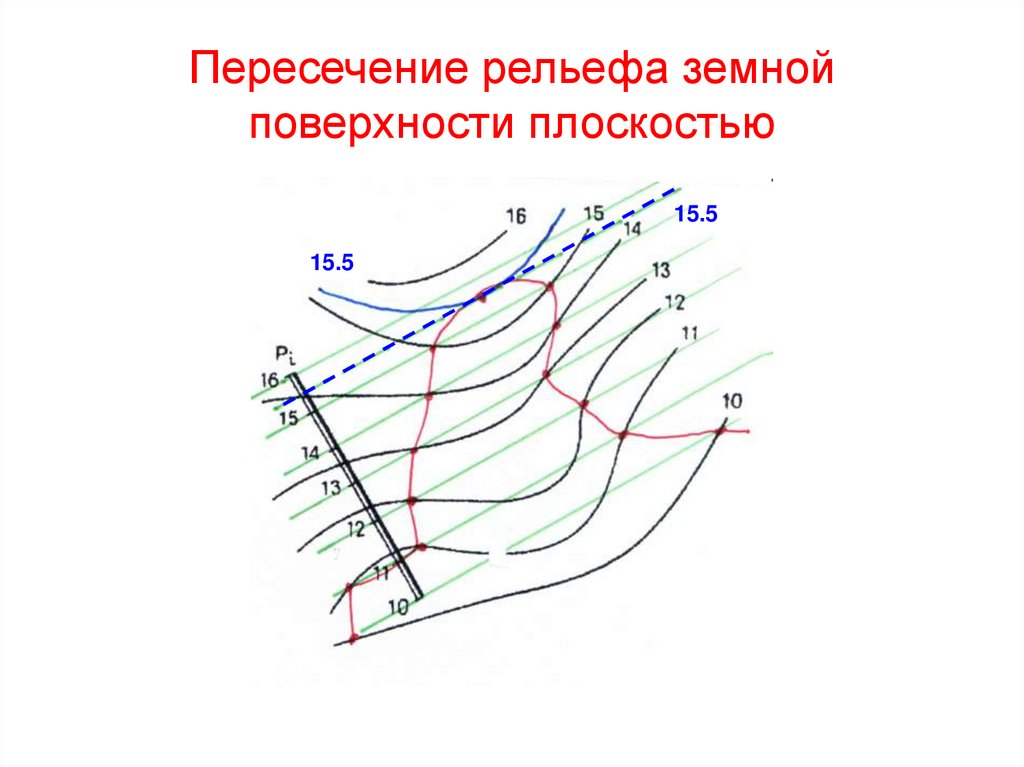
66. Пересечение рельефа земной поверхности плоскостью
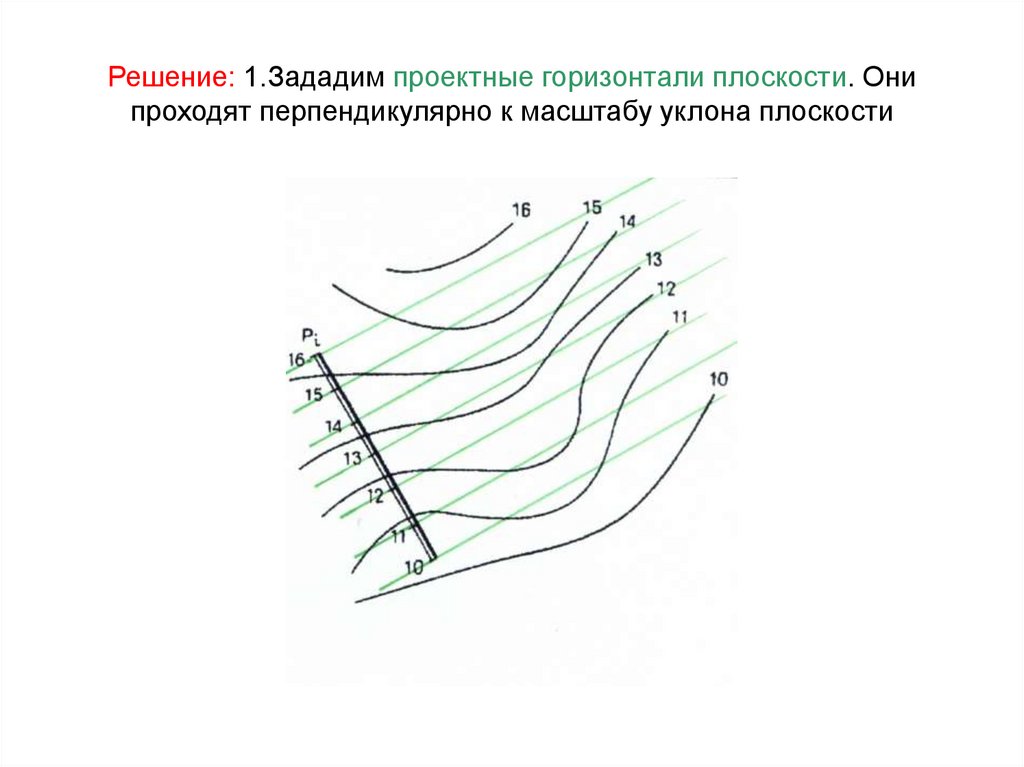
Задача 6.4 стр.49:67. Решение: 1.Зададим проектные горизонтали плоскости. Они проходят перпендикулярно к масштабу уклона плоскости
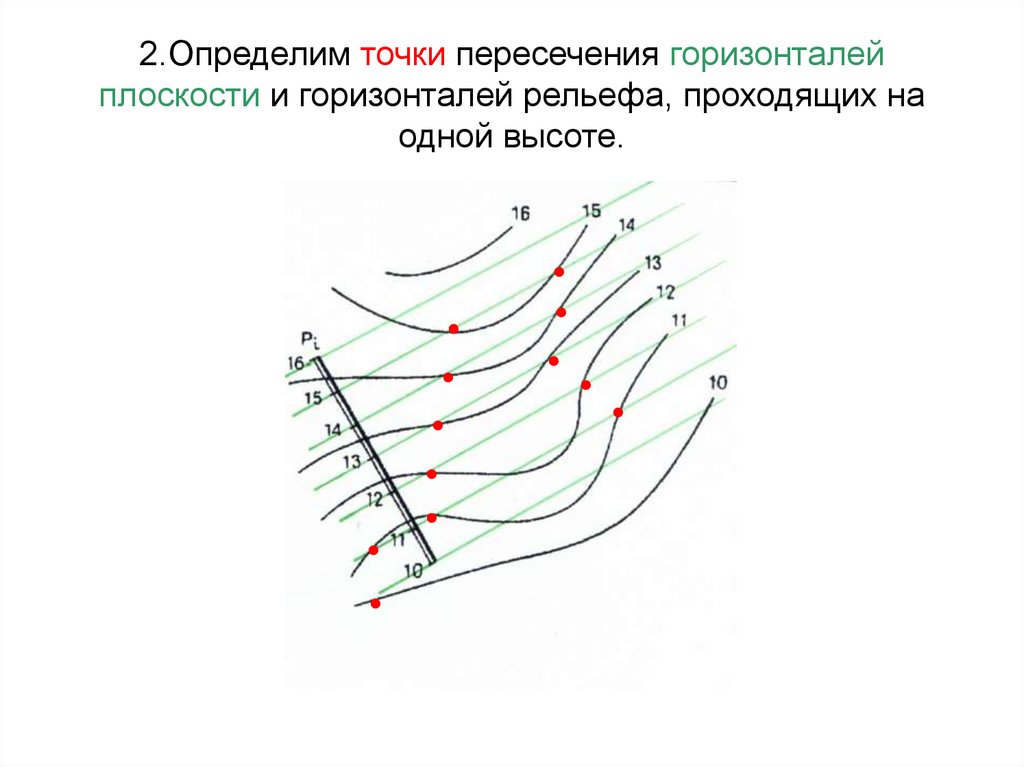
68. 2.Определим точки пересечения горизонталей плоскости и горизонталей рельефа, проходящих на одной высоте.
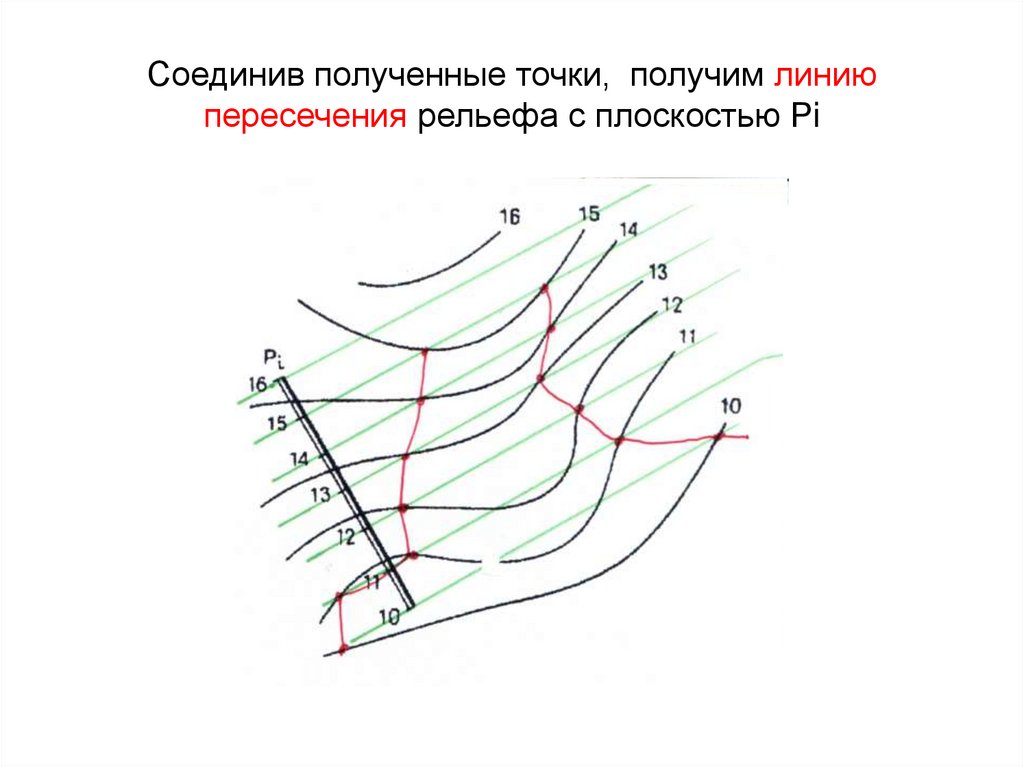
69. Соединив полученные точки, получим линию пересечения рельефа с плоскостью Рi
70. Т.к. горизонтали на высоте 16 м не пересеклись, задаем промежуточные проектные и рельефные горизонтали через 0,5 м (0,25м) и
определяем пиковую точку на пересечениигоризонталей , расположенных на высоте 15,5 м
15.5
15.5
71. Пересечение рельефа земной поверхности плоскостью
15.515.5
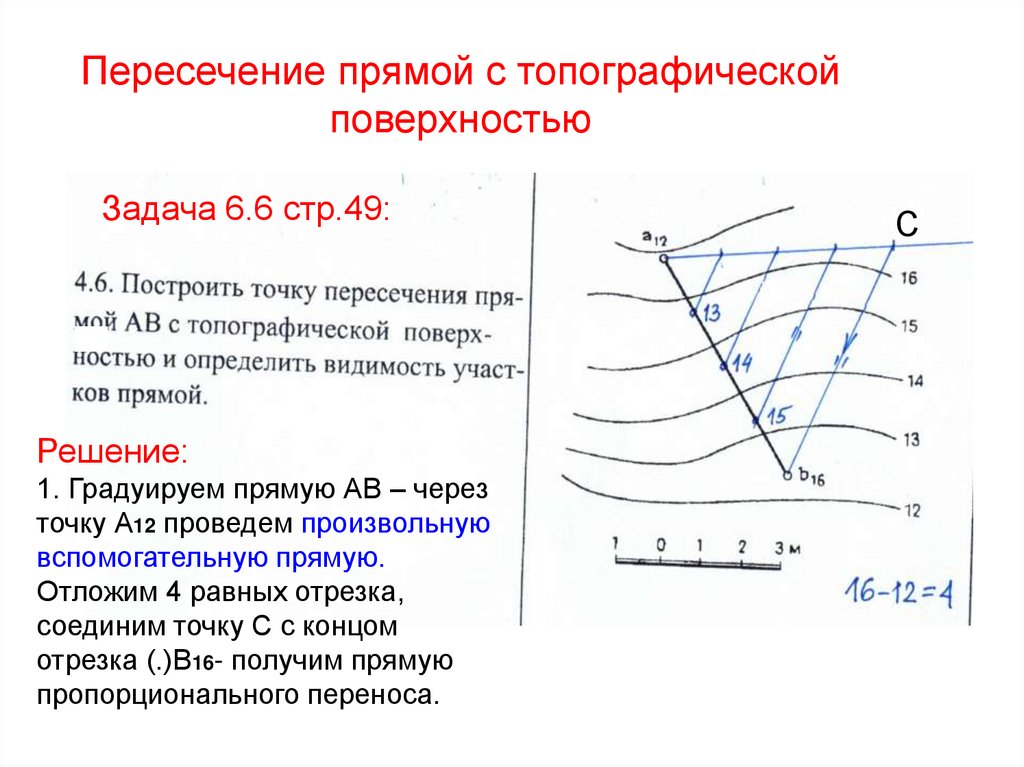
72. Пересечение прямой с топографической поверхностью
Задача 6.6 стр.49:Решение:
1. Градуируем прямую АВ – через
точку А12 проведем произвольную
вспомогательную прямую.
Отложим 4 равных отрезка,
соединим точку С с концом
отрезка (.)В16- получим прямую
пропорционального переноса.
С
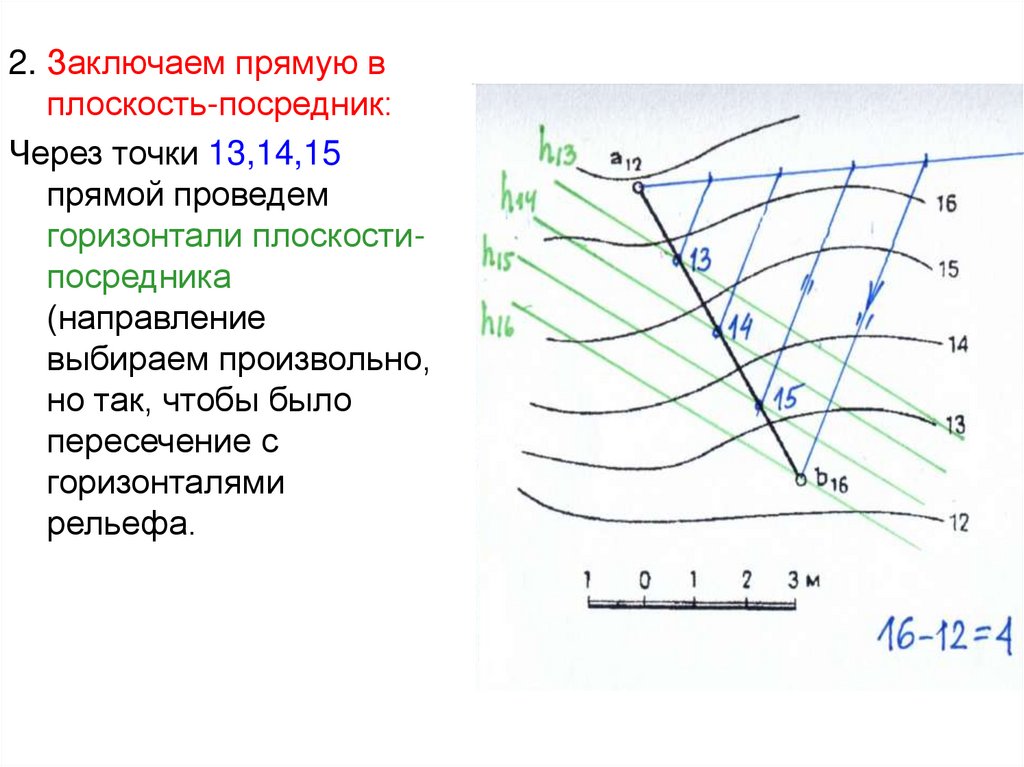
73.
2. Заключаем прямую вплоскость-посредник:
Через точки 13,14,15
прямой проведем
горизонтали плоскостипосредника
(направление
выбираем произвольно,
но так, чтобы было
пересечение с
горизонталями
рельефа.
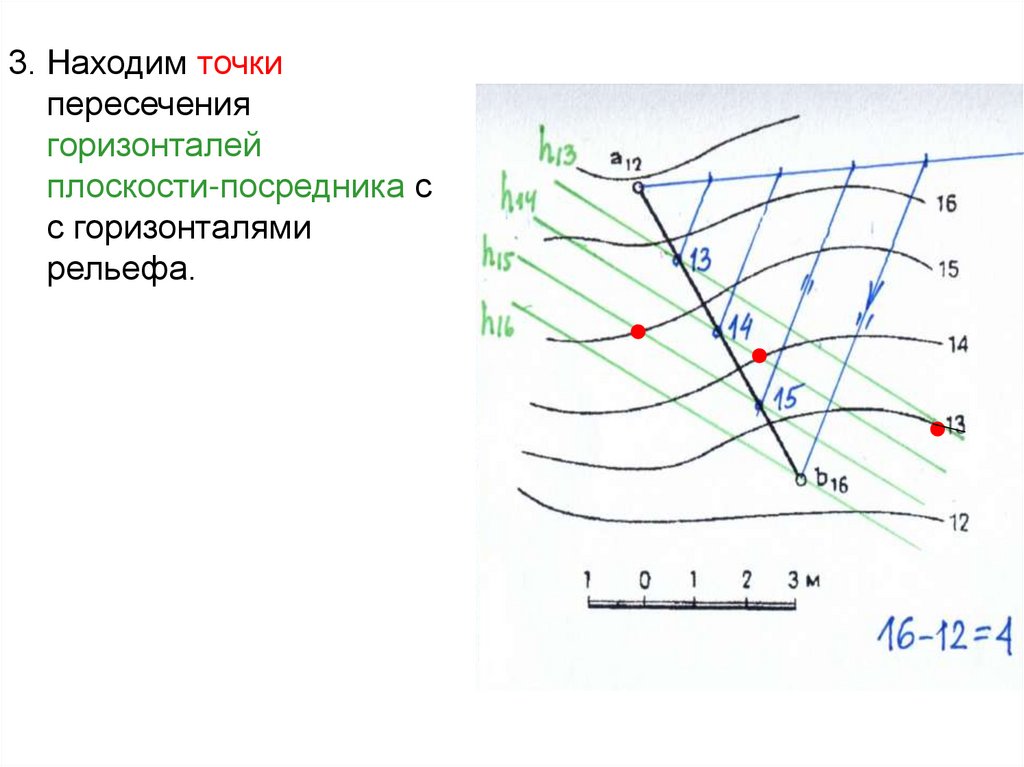
74.
3. Находим точкипересечения
горизонталей
плоскости-посредника с
с горизонталями
рельефа.
75.
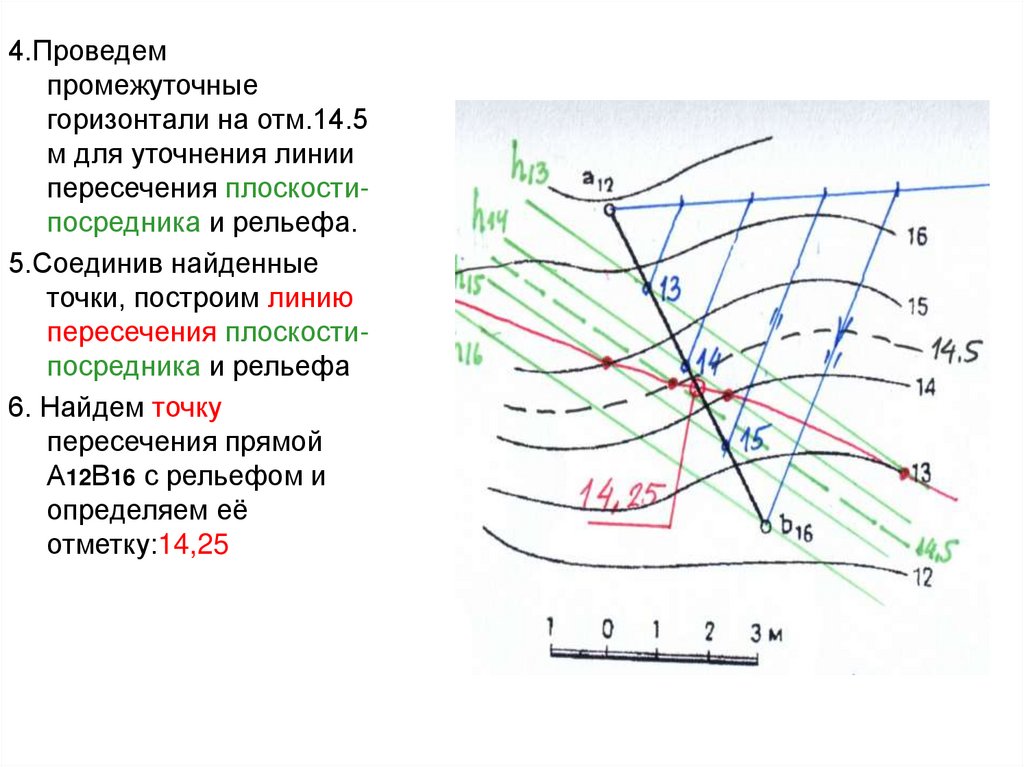
4.Проведемпромежуточные
горизонтали на отм.14.5
м для уточнения линии
пересечения плоскостипосредника и рельефа.
5.Соединив найденные
точки, построим линию
пересечения плоскостипосредника и рельефа
6. Найдем точку
пересечения прямой
А12В16 с рельефом и
определяем её
отметку:14,25
76.
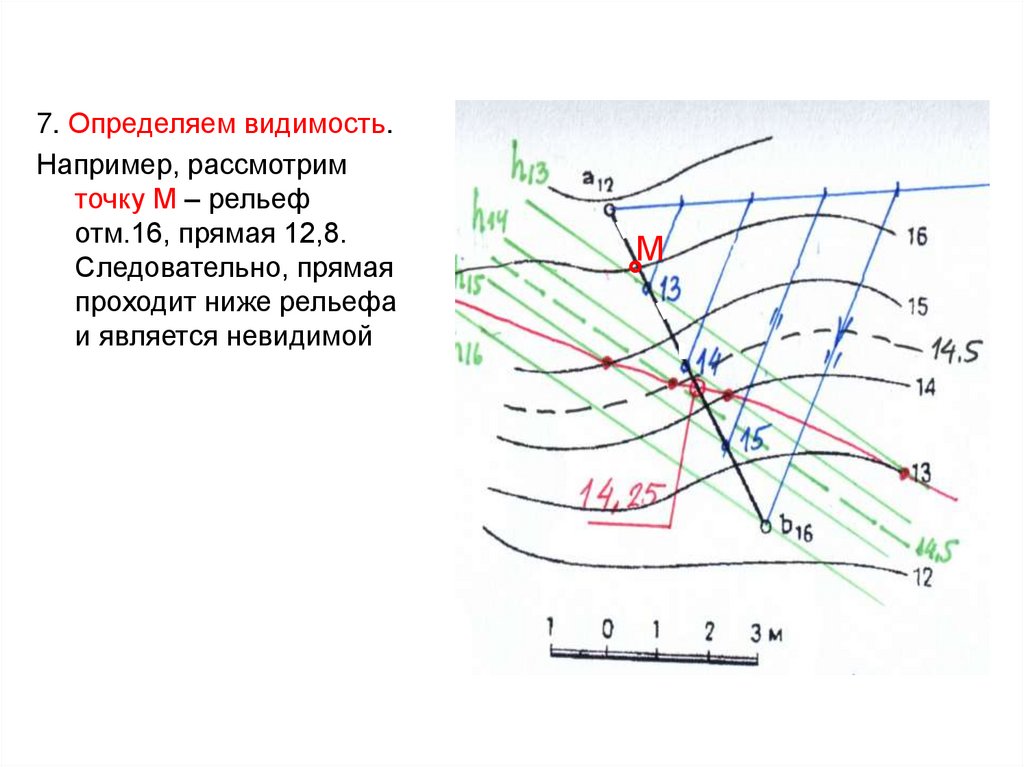
7. Определяем видимость.Например, рассмотрим
точку М – рельеф
отм.16, прямая 12,8.
Следовательно, прямая
проходит ниже рельефа
и является невидимой
М
°


















 drafting
drafting








