Similar presentations:
Решение тригонометрических уравнений приводимых к алгебраическим
1.
«Каждая решенная мною задачастановится образом, который служит
впоследствии для решения других задач»
Р.Декарт
Владимирова Р.В.
учитель математики
МБОУ «Гимназия № 94»
Московского района г.Казани
2.
1. Введение2. Повторение
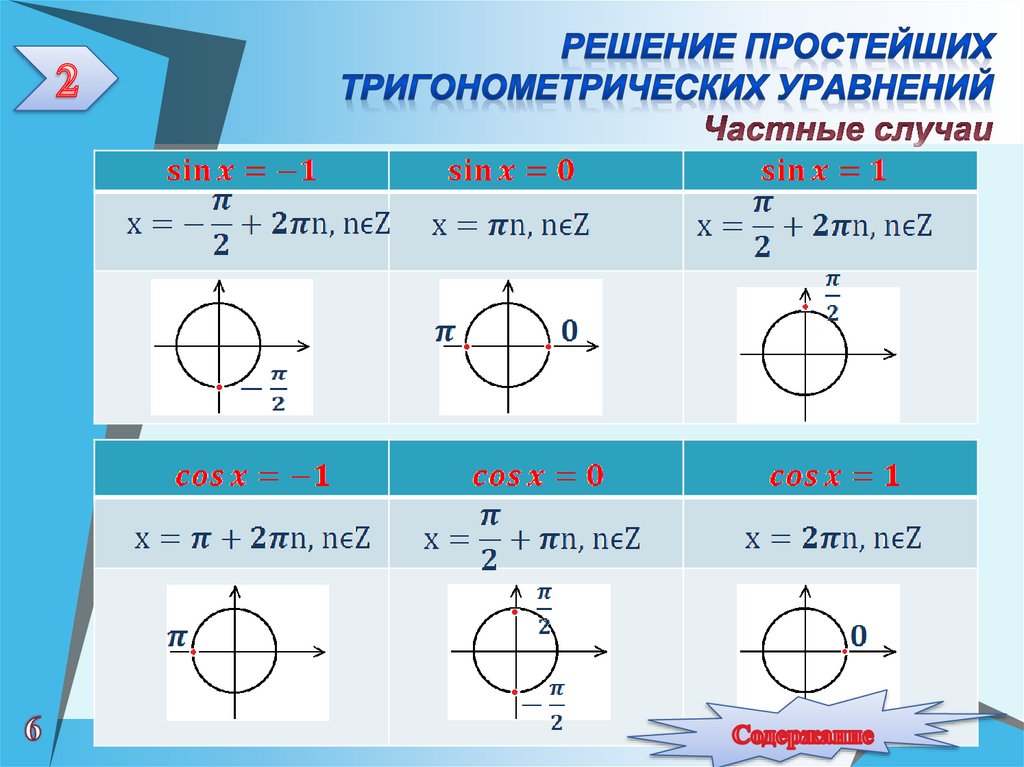
Простейшие тригонометрические уравнения
Частные случаи
Задания для на повторение
4. Уравнения, приводимых к алгебраическим
5. Примеры решения уравнений
6. Использование тр.ур. при решении
геометрических задач
7.Задания для самостоятельной работы
8.Краткий справочник формул
3.
Тригонометрические функции возникли вДревней Греции в связи с исследованиями в
астрономии и геометрии. Отношения сторон в
прямоугольном треугольнике, которые по
существу и есть тригонометрические функции,
встречаются уже в III в. до н.э. в работах
Евклида, Архимеда и других.
Современную форму тригонометрическим
функциям и вообще тригонометрии придал
Леонард Эйлер. Ему принадлежат определения
тригонометрических функций и принятая в наши
дни символика.
4.
ТРИГОНОМЕТРИЯматематическая
дисциплина, изучающая зависимость между
сторонами и углами треугольника.
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ, с
помощью которых связываются элементы
треугольника,
изучаются
в
курсе
математического анализа.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ –
это уравнения, в которых неизвестные
являются аргументами тригонометрических
функций.
-
5.
ЕслиЕсли
уравнение не имеет решения.
Если
Если
уравнение не имеет решения.
6.
7.
1. Решите( 1) n
1)
уравнение:
n,
4
n
,
4 2
3)
2 cos x
n Z
n Z
2 n 2) n 3)
3
3
n
4
2 n,
4
4)
2. Решите уравнение:
1)
2)
8
2
n Z
n Z
sin( 3x) 0
n 4)
n
3
1
3. Укажите наименьший
sin tg ( x)
положительный корень уравнения
2
3
1)
3
2)
5
4
3)
6
4)
2
8.
С помощью замены переменной можнопривести тригонометрическое уравнение к
алгебраическому. Рассмотрим несколько типов
уравнений:
Тип уравнения
Замена
Алгебраическое
уравнение
ПР №1
ПР №2
ПР №3
ПР №4
9.
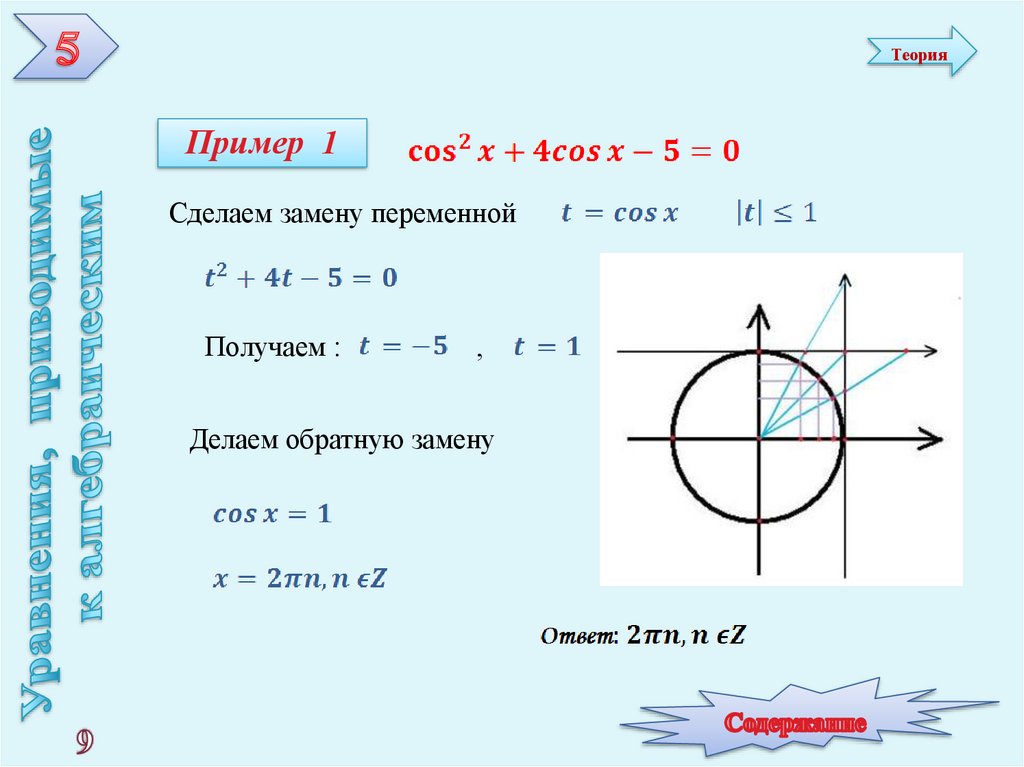
ТеорияПример 1
Сделаем замену переменной
Получаем :
,
Делаем обратную замену
,
10.
ТеорияПример 2
Применим основное тригонометрическое тождество
Сделаем замену переменной
Получаем :
,
11.
ТеорияПример 3
Сделаем замену переменной
Получаем :
,
12.
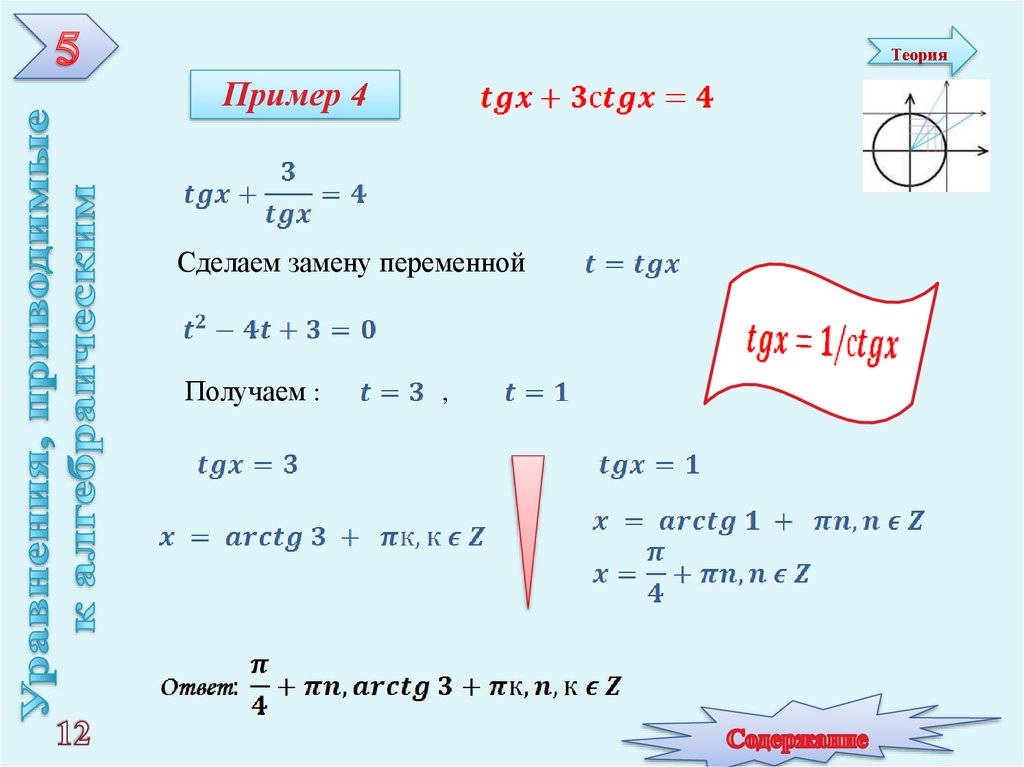
ТеорияПример 4
Сделаем замену переменной
Получаем :
,
13.
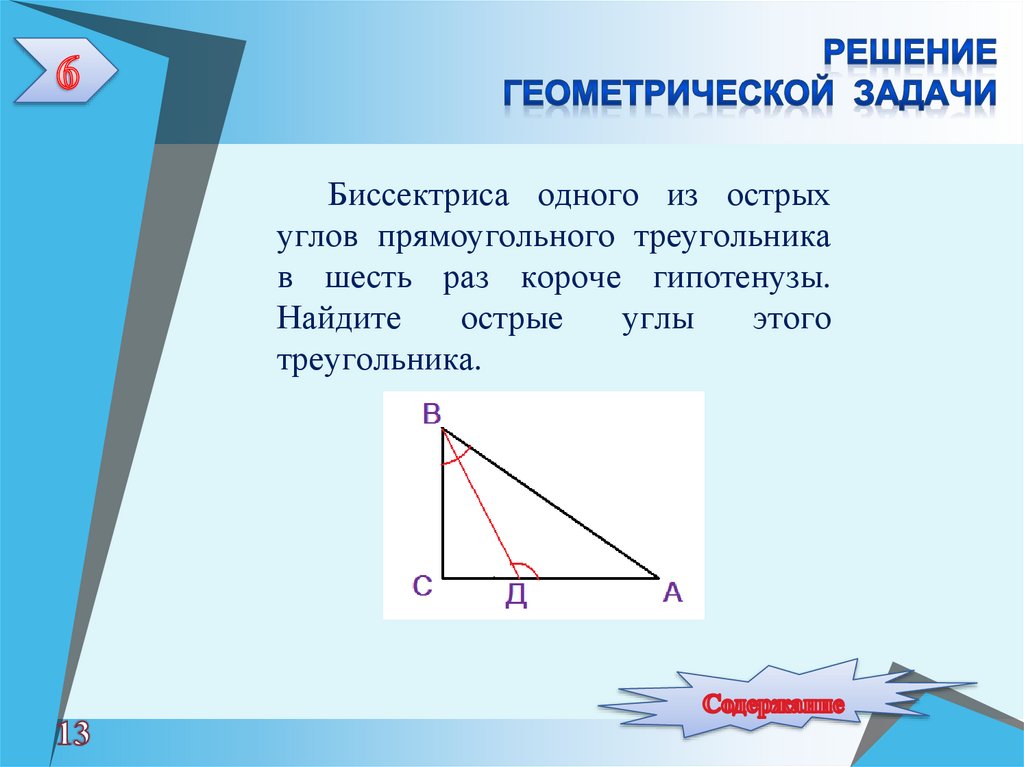
Биссектриса одного из острыхуглов прямоугольного треугольника
в шесть раз короче гипотенузы.
Найдите
острые
углы
этого
треугольника.
14.
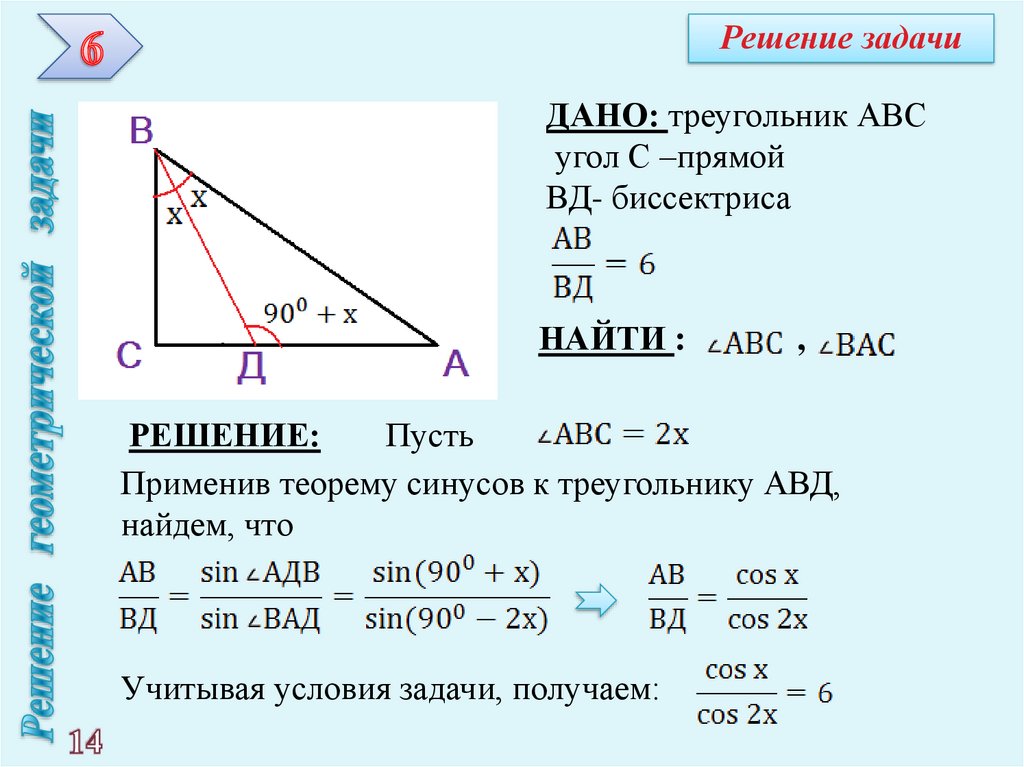
Решение задачиДАНО: треугольник АВС
угол С –прямой
ВД- биссектриса
НАЙТИ :
,
РЕШЕНИЕ:
Пусть
Применив теорему синусов к треугольнику АВД,
найдем, что
Учитывая условия задачи, получаем:
15.
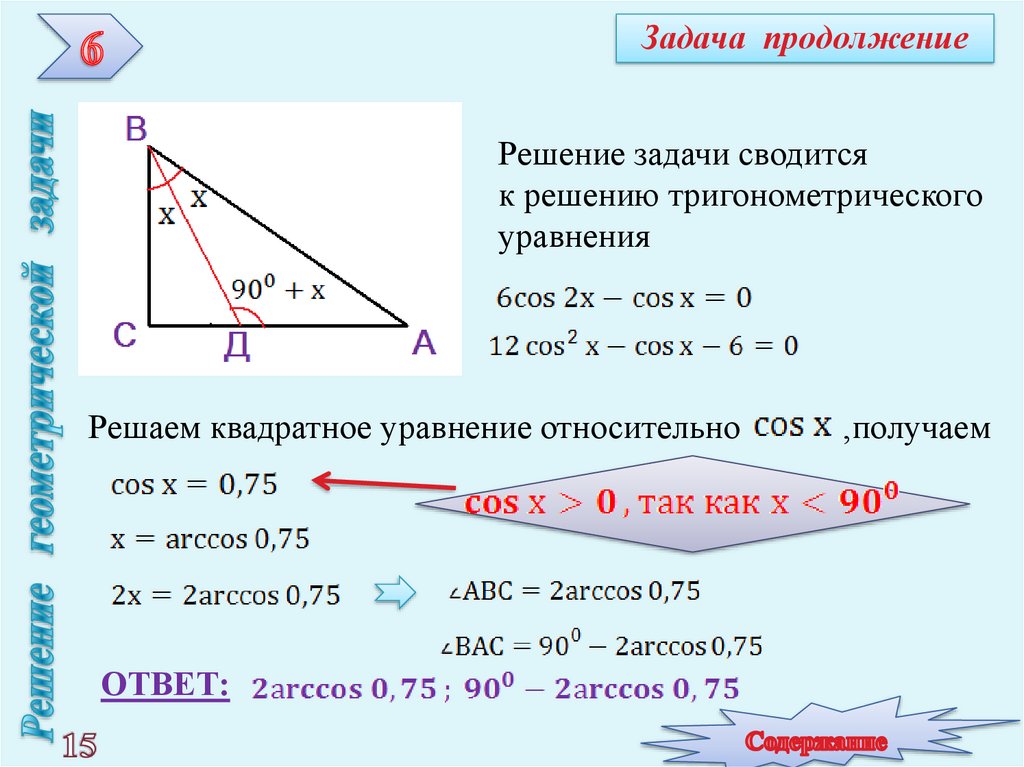
Задача продолжениеРешение задачи сводится
к решению тригонометрического
уравнения
Решаем квадратное уравнение относительно
ОТВЕТ:
,получаем
16.
Задания для самостоятельной работыВариант № 1
1)
Вариант № 2
1)
Ответы
2)
2)
3)
3)
4)
4)
5)
5)
17.
Ответы самостоятельной работыВариант № 1
Вариант № 2
1)
1)
2)
2)
3)
3)
4)
4)
5)
5)
Задания
18.
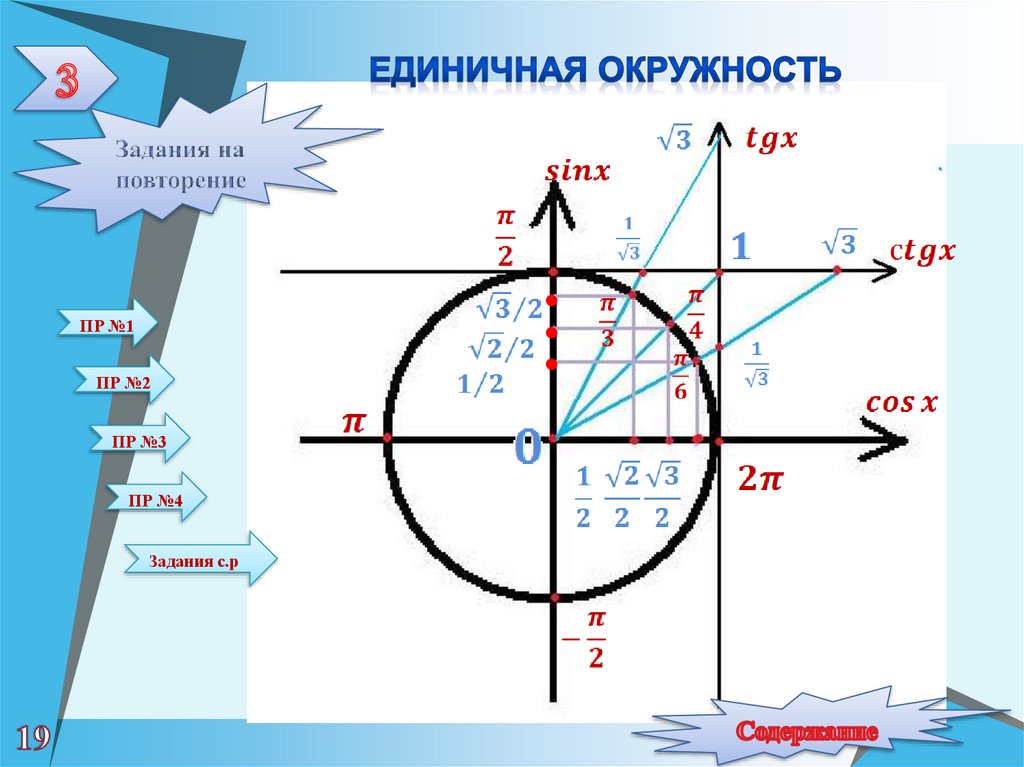
1. Нахождение тригонометрическихфункций по единичной окружности
2. Основные тригонометрические
тождества
3. Формулы двойного аргумента
4. Формулы сложения
5. Формулы преобразования суммы в
произведение
6. Формулы преобразования произведения
в сумму
19.
ПР №1ПР №2
ПР №3
ПР №4
Задания с.р
..
.
20.
2. Основныетригонометрические
тождества
3.Формулы
двойного
аргумента
1
7
2
8
3
9
4
10
5
11
6
12
21.
4. Формулы сложения1
2
3
4
5
6
7
8
22.
5. Формулы преобразования суммы впроизведение
1
2
3
4
6. Формулы преобразования
произведения в сумму
1
2
3















 mathematics
mathematics








