Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные уравнения

1.

Методическая разработка урока алгебры в 10 классе

2. Инструктаж по работе с оценочными листами

Оценочный лист
Фамилия, имя __________________________
класс ____________
Название
1. «Я и домашнее задание»
2. Обратные функции
3. Кодирование «Уравнение ↔ корни»
4. Работа в группе
5. Самостоятельная работа «Решаю сам»
Средняя оценка
Оценка

3.

«Величие человека –
в его способности
мыслить»
Блез Паскаль

4.

«В математических
вопросах
нельзя
пренебрегать даже
самыми
мелкими
ошибками»
Исаак Ньютон

5. Моноторинг «Я и домашнее задание»

Вариант 1
π
+ πn, nϵ Z
6
π π
2. х = ±
+ n, nϵ Z
6 4
Вариант 2
π 2π
n , nϵ Z
+
4 3
π
2. х =
+ πn, nϵ Z
12
1. х = ±
1. х = ±
3. х = ± 3π + 8πn, nϵ Z
4. х = - π - 2πn,
2
х = π - 2πn, nϵ Z
3. х = ± 2π + 6πn, nϵ Z
π
4. х = - - 2πn,
2
5π
х=
- 2πn, nϵ Z
6
π
2π 4π 5π
*5. х = ± ; ±
;;3
3
3
3
π
13π 11π
*5. х = ±
;±
;±
18
18
18
Оценивание:
4 верно решенных примера - оценка «5»; 3 верно решенных – «4»; 2 – «3»
менее 2 – «2»

6.

«...Математика - это
цепь понятий: выпадет
одно звенышко - и не
понятно
будет
дальнейшее»
Н.К. Крупская

7. Разминка «Найди ошибку»

1
• arccos 60˚ = 2
1
arccos 2 = 3
• arcsin 0 = 1
arcsin 0 = 0
• arccos(• arcctg(-
2
2
π
)= - 4
π
1
)
=
6
3
3
4
arccos(-
2
2
arcctg(-
2
1
)=
3
3
)=

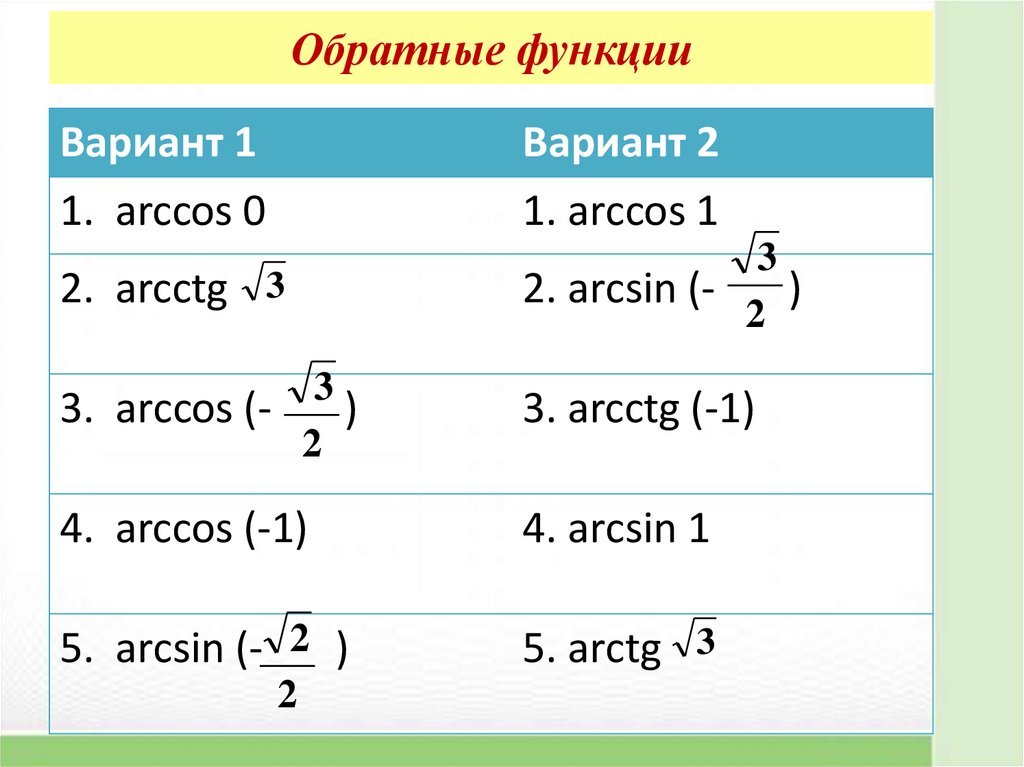
8. Обратные функции

Вариант 1
1. arccos 0
Вариант 2
1. аrсcos 1
2. arcctg 3
3
2. arсsin ()
2
3
3. аrсcos ()
2
3. arcctg (-1)
4. аrcсos (-1)
4. arсsin 1
5. arсsin (- 2 )
5. arсtg 3
2

9. Проверка. Обратные функции

Вариант 1
π
1.
2
π
2.
6
Вариант 2
5π
3.
6
3π
3.
4
π
4.
2
π
5.
3
4. π
π
5. 4
1. 0
π
2. - 3

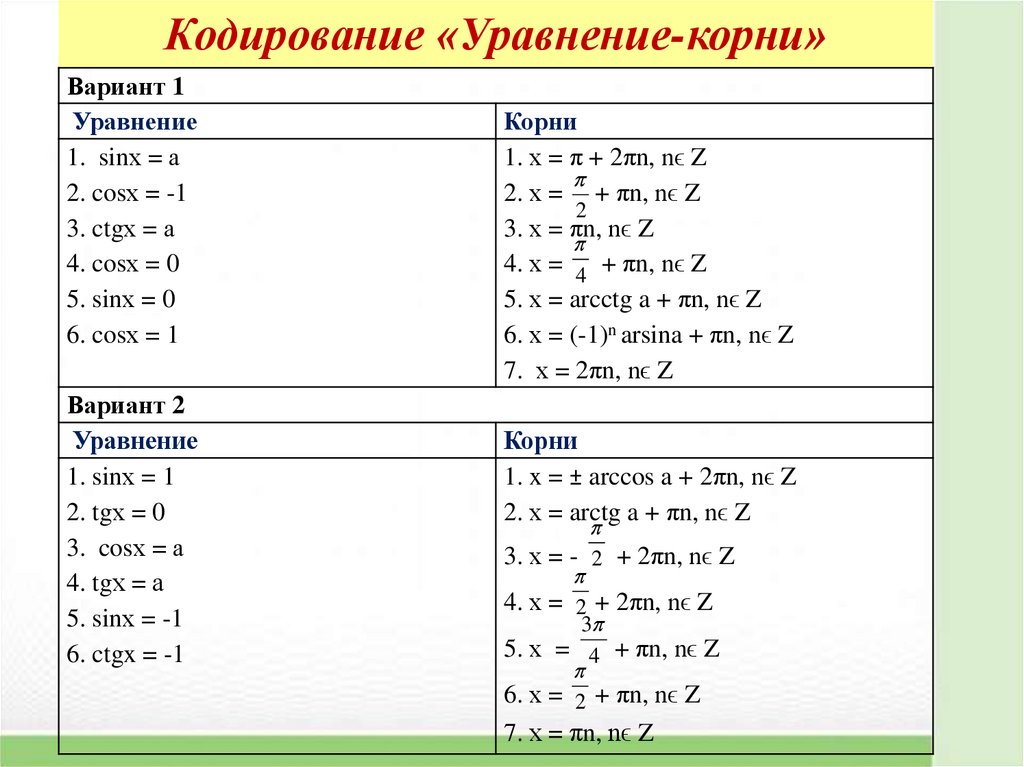
10. Кодирование «Уравнение-корни»

Вариант 1
Уравнение
1. sinх = а
2. cosх = -1
3. ctgх = а
4. cosх = 0
5. sinх = 0
6. cosх = 1
Вариант 2
Уравнение
1. sinх = 1
2. tgх = 0
3. cosх = а
4. tgх = а
5. sinх = -1
6. ctgx = -1
Корни
1. х = π + 2πn, nϵ Z
2. х = + πn, nϵ Z
2
3. х = πn, nϵ Z
4. х = 4 + πn, nϵ Z
5. х = arcctg a + πn, nϵ Z
6. х = (-1)n arsina + πn, nϵ Z
7. х = 2πn, nϵ Z
Корни
1. x = ± arccos a + 2πn, nϵ Z
2. х = arctg a + πn, nϵ Z
3. х = - 2 + 2πn, nϵ Z
4. х = 2 + 2πn, nϵ Z
3
5. х = 4 + πn, nϵ Z
6. х = 2 + πn, nϵ Z
7. х = πn, nϵ Z

11. Проверка кодирования «Уравнение-корни»

Вариант 1
16
21
35
4 2
5 3
67
Вариант 2
14
27
31
42
53
65
Оценивание:
6 верно решенных примера - оценка «5»
4-5 – «4»
3 – «3»
менее 3 – «2»

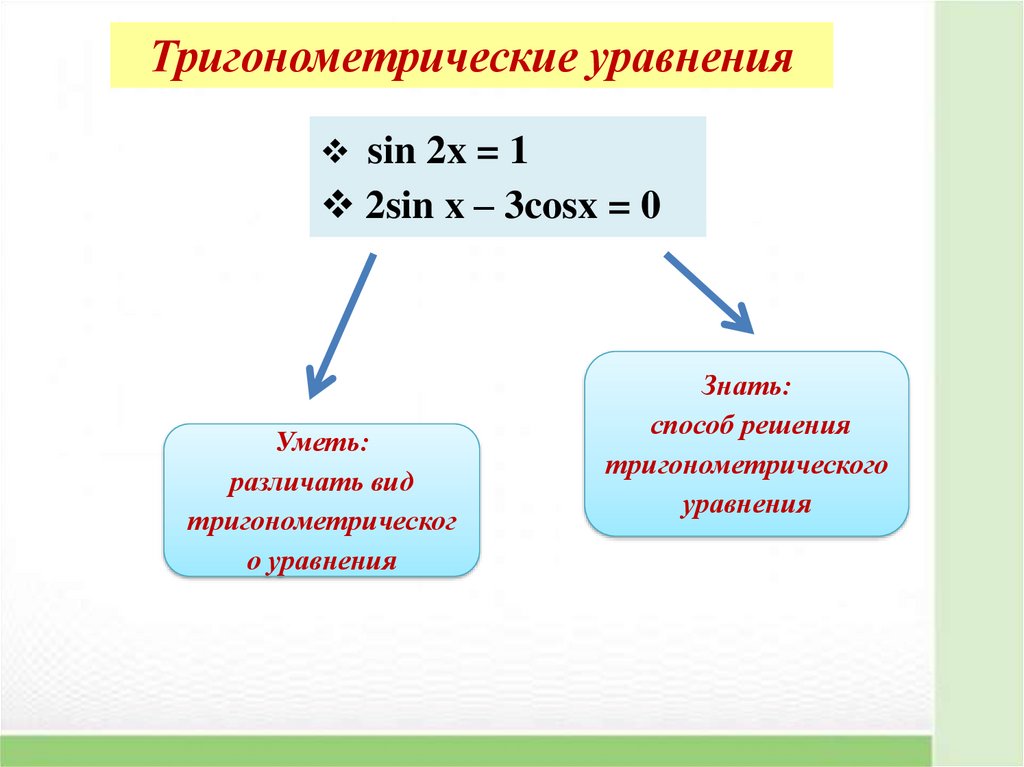
12.

Тригонометрические уравнения
sin 2x = 1
2sin x – 3cosx = 0
Уметь:
различать вид
тригонометрическог
о уравнения
Знать:
способ решения
тригонометрического
уравнения

13. Я – исследователь

Как решить любое задание
С1,
содержащее
тригонометрическое
уравнение, на предстоящем
экзамене?

14.

правильно
неправильно

15. Тема урока: «Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные уравнения»

• Линейные
• Квадратные
• Кубические
• Биквадратные

16. Основные методы решения тригонометрических уравнений

• Метод разложения на
множители
• Метод введения новой
переменной
• Функциональнографический метод

17. Исследование

1. Соотнести свое уравнение с одним из
типов уравнений, используя
справочный материал
2. Решить данное уравнение
3. Составить алгоритм решения
4. Одному члену группы защитить
совместно решенное уравнение (основные
формулы, преобразования, метод)
5. Зафиксировать возможные ошибки и
составить рекомендации для работы с
заданиями такого типа

18. Результаты исследования

Алгоритм решения методом замены уравнений,
сводящимся к алгебраическим
1. Привести уравнение к алгебраическому виду
относительно одной из тригонометрических функций
2. Обозначить полученную функцию переменной,
обозначив ее ограничения
3. Записать и решить полученное алгебраическое
уравнение
4. Вернуться к замене
5. Решить простейшее тригонометрическое уравнение

19. Результаты исследования

Алгоритм решения методом замены однородных
уравнений
sin n x 0
cos n xоднородное
0
1. Разделить
уравнение на
или на
Если уравнение первой степени, то переход к п.5.
2. Обозначить полученную функцию переменной,
обозначив ее ограничения.
3. Записать и решить полученное алгебраическое
уравнение.
4. Вернуться к замене.
5. Решить простейшее тригонометрическое уравнение.

20.

Спасибо
за
урок!