Similar presentations:
Основы расчета деревянных конструкций
1.
ОСНОВЫ РАСЧЕТАДЕРЕВЯННЫХ КОНСТРУКЦИЙ
2.
Предельные состоянияПредельным называется такое состояние
конструкций, при котором их дальнейшая эксплуатация
становится невозможной по причине:
1) потери несущей способности – I группа
предельных состояний
2) возникновения недопустимых деформаций –
II группа предельных состояний .
Предельные состояния могут наступать:
- под влиянием условий работы деревянных
конструкций;
- качества, размеров и свойств материалов.
3.
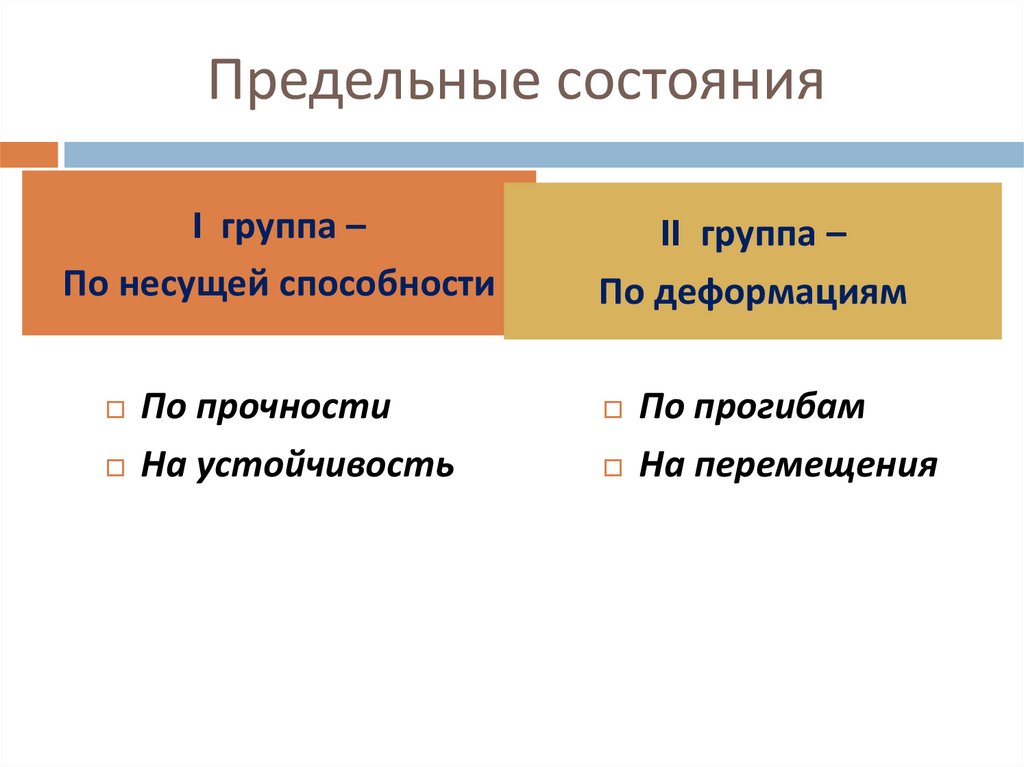
Предельные состоянияI группа –
По несущей способности
По прочности
На устойчивость
II группа –
По деформациям
По прогибам
На перемещения
4.
Предельные состоянияПервая группа предельных состояний - наиболее
ответственная.
В ДК могут возникать следующие предельные
состояния первой группы:
разрушение,
потеря устойчивости,
опрокидывание,
недопустимая ползучесть.
5.
Предельные состоянияЭти предельные состояния не наступают, если выполняются
условия:
σ ≤ R,
τ ≤ Rск (или Rср),
т.е. когда нормальные напряжения (σ) и касательные
напряжения (τ) не превышают некоторой предельной
величины R, называемой расчетным сопротивлением.
6.
Расчетные сопротивления древесиныРасчетные сопротивления древесины в зависимости от условий работы и
эксплуатации корректируются путем умножения их на коэффициенты, т.е.
подсчитываются как:
R = Rт•mп•mв•mн•mб•mсл•mгн
где Rт - расчетное сопротивление древесины сосны или ели, принимается
по табл.3 (СП 64.13330.2016);
mп - переходный коэффициент на породу древесины;
mв - коэффициент условия работы на температурно-влажностный режим
эксплуатации;
mн - коэффициент условий работы при воздействии
кратковременных
нагрузок;
mб - коэффициент, учитывающий абсолютную высоту деревянного элемента
(клееного);
mсл - коэффициент (для клееной древесины);
mгн - коэффициент (для клееной древесины).
Коэффициенты принимаются по СП 64.13330.2016 ДК п.п.3.1-3.2
7.
Предельные состоянияВторая группа предельных состояний характеризуется такими
признаками, при которых эксплуатация конструкций или сооружений хотя
и затруднена, однако, полностью не исключается, т.е. конструкция
становится непригодной только к нормальной эксплуатации.
Пригодность конструкции к нормальной эксплуатации обычно
определяется по прогибам:
f ≤ [f], или
f/l ≤ [f/l].
Это означает, что изгибаемые элементы или конструкции пригодны к
нормальной эксплуатации, когда наибольшая величина отношения прогиба
к пролету меньше предельно допустимого относительного прогиба [f/l]
(по СП 20.133300.2018 с изм. Нагрузки и воздействия).
8.
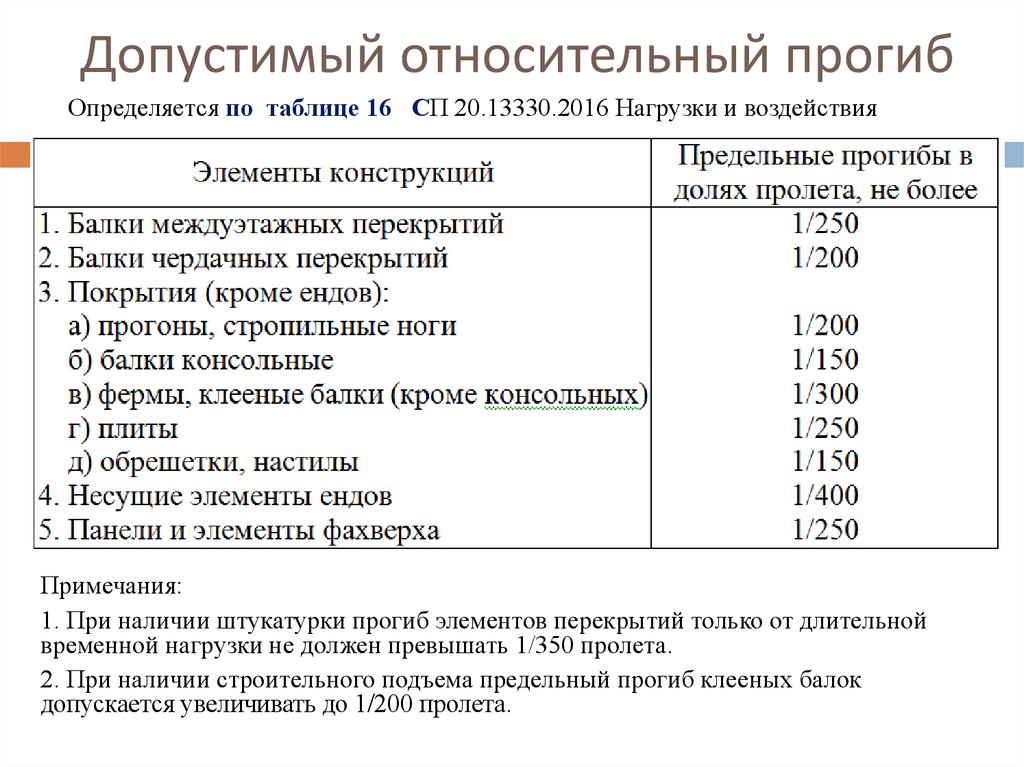
Допустимый относительный прогибОпределяется по таблице 16 СП 20.13330.2016 Нагрузки и воздействия
Примечания:
1. При наличии штукатурки прогиб элементов перекрытий только от длительной
временной нагрузки не должен превышать 1/350 пролета.
2. При наличии строительного подъема предельный прогиб клееных балок
допускается увеличивать до 1/200 пролета.
9.
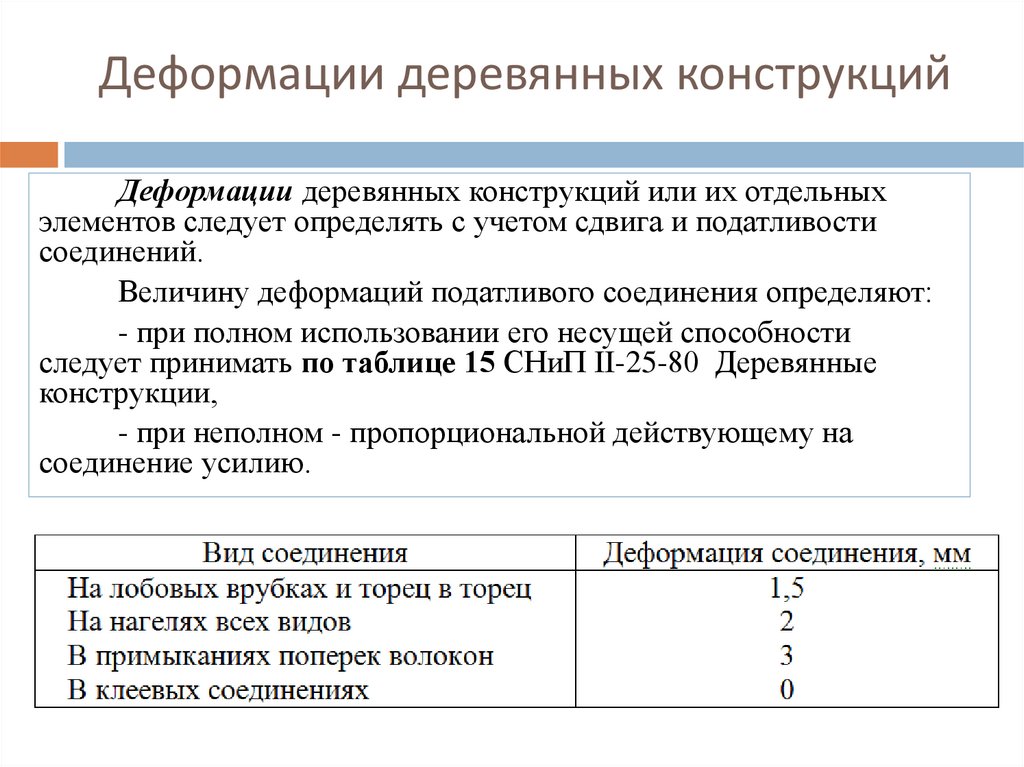
Деформации деревянных конструкцийДеформации деревянных конструкций или их отдельных
элементов следует определять с учетом сдвига и податливости
соединений.
Величину деформаций податливого соединения определяют:
- при полном использовании его несущей способности
следует принимать по таблице 15 СНиП II-25-80 Деревянные
конструкции,
- при неполном - пропорциональной действующему на
соединение усилию.
10.
РАСЧЕТ ЭЛЕМЕНТОВДЕРЕВЯННЫХ КОНСТРУКЦИЙ
Расчет элементов деревянных
конструкций по предельным состояниям
первой группы
11.
Расчет элементов деревянных конструкций попредельным состояниям первой группы
Рекомендации по расчету приведены в СП 64.13330.2016
Деревянные конструкции, глава 4 в зависимости от:
- вида элемента – цельный, клееный, составной;
- вида загружения
Виды загружения:
- центрально-растянутые и центрально-сжатые элементы;
- изгибаемые элементы;
- элементы, подверженные действию осевой силы с изгибом
(внецентренно-сжатые и внецентренно-растянутые элементы).
12.
РАСЧЕТ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХКОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ
СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
Центрально-растянутые элементы
13.
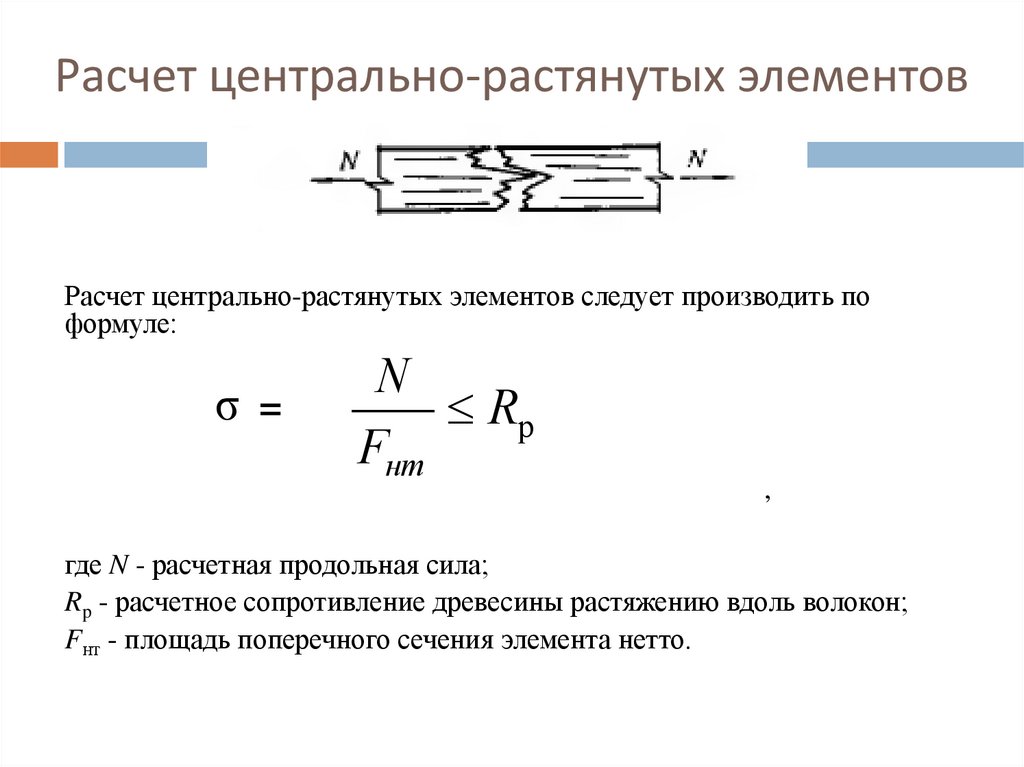
Расчет центрально-растянутых элементовРасчет центрально-растянутых элементов следует производить по
формуле:
σ =
N
Rр
Fнт
,
где N - расчетная продольная сила;
Rp - расчетное сопротивление древесины растяжению вдоль волокон;
Fнт - площадь поперечного сечения элемента нетто.
14.
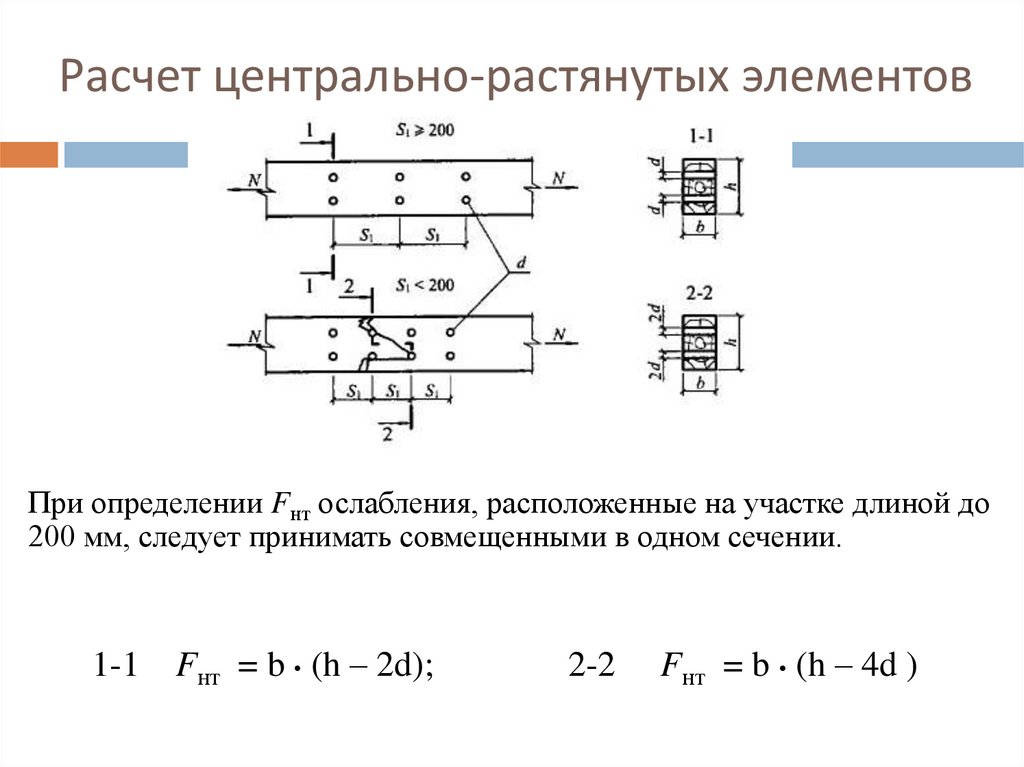
Расчет центрально-растянутых элементовПри определении Fнт ослабления, расположенные на участке длиной до
200 мм, следует принимать совмещенными в одном сечении.
1-1
Fнт = b • (h – 2d);
2-2
Fнт = b • (h – 4d )
15.
РАСЧЕТ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХКОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ
СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
Центрально-сжатые элементы
16.
Расчет центрально-сжатых элементовРасчет центрально-сжатых элементов постоянного цельного сечения следует
производить по формулам:
а) на прочность
N
σ = Fнт Rс
,
б) на устойчивость
σ
N
Rс
= Fрас
,
где Rс - расчетное сопротивление древесины сжатию вдоль волокон;
коэффициент продольного изгиба, определяемый согласно п. 4.3
СП ДК;
Fнт площадь нетто поперечного сечения элемента;
Fрас - расчетная площадь поперечного сечения элемента.
17.
Расчет центрально-сжатых элементова)
б)
Fрас - расчетная площадь поперечного сечения элемента,
принимаемая равной:
при отсутствии ослаблений или ослаблениях в опасных
сечениях, не выходящих на кромки (рис. а), если
площадь ослаблений не превышает 25 % Fбр,
Fрасч = Fбр,
где Fбр - площадь сечения брутто;
при ослаблениях, не выходящих на кромки, если
площадь ослабления превышает 25 % Fбр,
Ослабление сжатых
элементов:
а -не выходящие на
кромку;
б - выходящие на кромку
Fрас = 4/3 Fнт;
при симметричных ослаблениях, выходящих на кромки
(рис. б),
Fрас = Fнт.
18.
Расчет центрально-сжатых элементовКоэффициент продольного изгиба φ всегда меньше 1
(принимается согласно п.п. 4.3 СП ДК), учитывает влияние
устойчивости на снижение несущей способности сжатого элемента
в зависимости от его расчетной максимальной гибкости λ.
Гибкость сжатых элементов λ ограничивается с тем, чтобы они
не получились недопустимо гибкими и недостаточно надежными.
Отдельные элементы конструкций (отдельные стойки, пояса,
опорные раскосы ферм и т.п.) должны иметь гибкость не более
120.
Другие 150, 175 или 200.
19.
Расчет центрально-сжатых элементовГибкость элементов и их отдельных ветвей в деревянных
конструкциях не должна превышать значений, указанных в
табл. 14 СП ДК.
Примечание.
Для сжатых элементов переменного сечения величины
предельной гибкости макс умножаются на , где коэффициент
kжN принимается по табл. 1 прил. 4 СНиП ДК.
20.
Расчет центрально-сжатых элементовПри гибкости более 70 (λ>70) сжатый элемент теряет
устойчивость, когда напряжения сжатия в древесине еще невелики и
она работает упруго.
Коэффициент продольного изгиба (или коэффициент
устойчивости), равный отношению напряжения в момент потери
устойчивости σкр к пределу прочности при сжатии Rпр, определяют по
формуле Эйлера с учетом постоянного отношения модуля упругости
древесины к пределу прочности E / Rпр = 312:
А
2
,
Где коэффициент А = 3000 для древесины и А = 2500 для
фанеры.
21.
Расчет центрально-сжатых элементовПри гибкостях, равных и меньших 70 (λ≤70) элемент теряет
устойчивость, когда напряжения сжатия достигают
упругопластической стадии и модуль упругости древесины
понижается. Коэффициент продольного изгиба при этом
определяют с учетом переменного модуля упругости по
упрощенной теоретической формуле:
1 a
100 ,
2
где коэффициент а = 0,8 для древесины и а = 1 для фанеры
22.
Расчет центрально-сжатых элементовГибкость элементов цельного сечения определяют по формуле:
l0
,
r
где lо - расчетная длина элемента;
r - радиус инерции сечения элемента с максимальными
размерами брутто соответственно относительно осей Х и У.
Для прямоугольного сечения размером hxb радиусы инерции
можно подсчитывать по формулам:
rx=0,289∙h,
ry=0,289∙b
23.
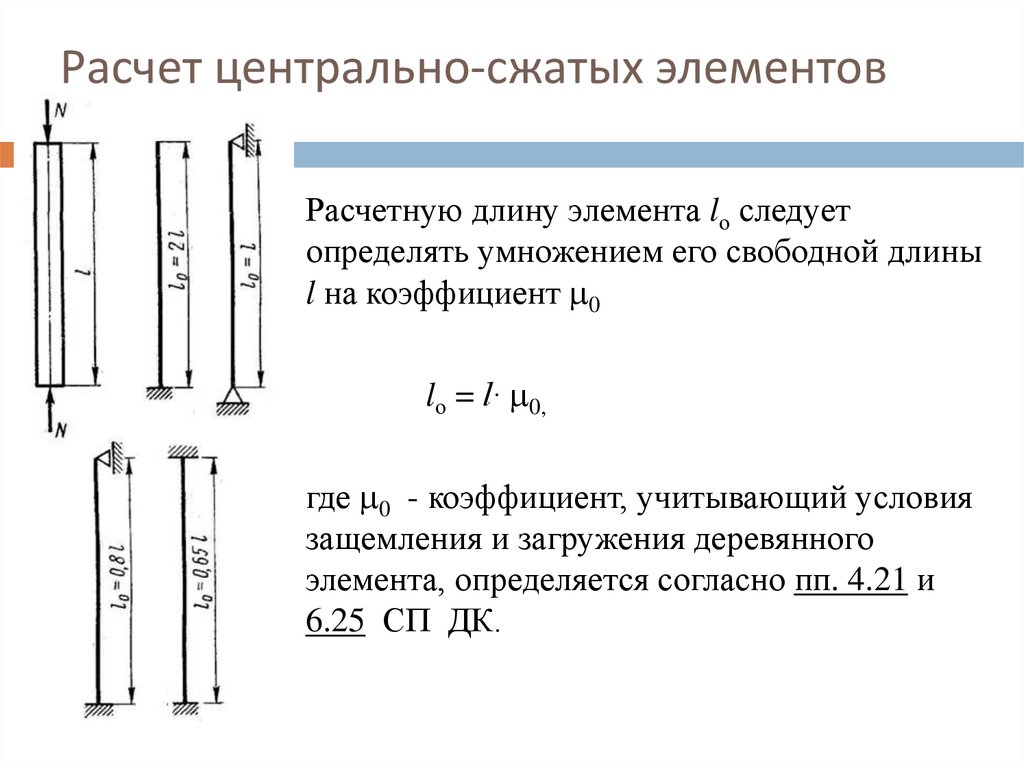
Расчет центрально-сжатых элементовРасчетную длину элемента lо следует
определять умножением его свободной длины
l на коэффициент 0
lо = l∙ 0,
где 0 - коэффициент, учитывающий условия
защемления и загружения деревянного
элемента, определяется согласно пп. 4.21 и
6.25 СП ДК.
24.
Расчет центрально-сжатых элементовРасчет на устойчивость центрально-сжатых элементов переменного
по высоте сечения следует выполнять по формуле:
N
Rс
Fм аксk жN
,
где Fмакс - площадь поперечного сечения брутто с максимальными
размерами;
kжN - коэффициент, учитывающий переменность высоты сечения,
определяемый по табл. 1 прил. 4 СП ДК (для элементов постоянного
сечения kжN = 1);
- коэффициент продольного изгиба, определяемый по п. 4.3 СП ДК для
гибкости, соответствующей сечению с максимальными размерами.
25.
РАСЧЕТ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХКОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ
СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
Изгибаемые элементы
26.
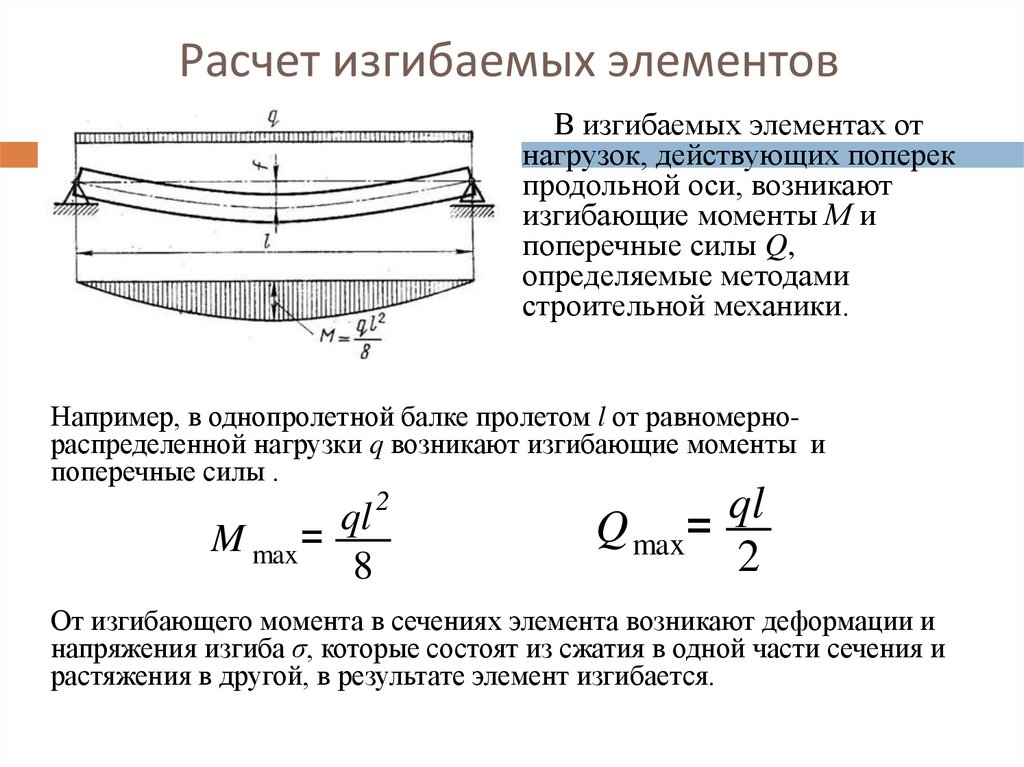
Расчет изгибаемых элементовВ изгибаемых элементах от
нагрузок, действующих поперек
продольной оси, возникают
изгибающие моменты М и
поперечные силы Q,
определяемые методами
строительной механики.
Например, в однопролетной балке пролетом l от равномернораспределенной нагрузки q возникают изгибающие моменты и
поперечные силы .
2
ql
M max =
ql
8
Q max=
2
От изгибающего момента в сечениях элемента возникают деформации и
напряжения изгиба σ, которые состоят из сжатия в одной части сечения и
растяжения в другой, в результате элемент изгибается.
27.
Расчет изгибаемых элементовРасчет изгибаемых элементов, обеспеченных от потери устойчивости
плоской формы деформирования (см. пп. 4.14 и 4.15 СП ДК), на прочность по
нормальным напряжениям следует производить по формуле
M
≤ Ru
σ=
W расч
,
где М - расчетный изгибающий момент;
Rи - расчетное сопротивление изгибу;
Wрасч - расчетный момент сопротивления поперечного сечения элемента.
Для цельных элементов
Wрасч = Wнт;
При определении Wнт ослабления сечений, расположенные на участке
элемента длиной до 200 мм, принимают совмещенными в одном сечении.
28.
Расчет изгибаемых элементовДля наиболее распространенного прямоугольного сечения:
3
2
I
bh
W=
=
h/2
6;
bh
I=
12
.
Подбор сечения изгибаемых элементов производится по
этой же формуле:
М
W тр =
Ru
,
затем, задавая один из размеров сечения (b или h), находят
другой размер.
29.
Расчет изгибаемых элементовРасчет на устойчивость плоской формы
деформирования изгибаемых элементов
прямоугольного постоянного сечения следует
производить по формуле:
M
σ = W Rи
M бр
,
(
где М - максимальный изгибающий момент на
рассматриваемом участке lр;
Wбр - максимальный момент сопротивления
брутто на рассматриваемом участке lp ;
φм – коэффициент устойчивости.
30.
Расчет изгибаемых элементовКоэффициент М для изгибаемых элементов прямоугольного
постоянного поперечного сечения, шарнирно-закрепленных от смещения
из плоскости изгиба и закрепленных от поворота вокруг продольной оси
в опорных сечениях, следует определять по формуле:
М
b2
140
kф
l ph
,
где lp расстояние между опорными сечениями элемента, а при
закреплении сжатой кромки элемента в промежуточных точках от
смещения из плоскости изгиба - расстояние между этими точками;
b - ширина поперечного сечения;
h - максимальная высота поперечного сечения на участке lp;
kф - коэффициент, зависящий от формы эпюры изгибающих
моментов на участке lp, определяемый по табл. 2 прил. 4 СП ДК.
31.
Расчет изгибаемых элементовПри расчете изгибаемых элементов с линейно меняющейся
по длине высотой и постоянной шириной поперечного сечения,
не имеющих закреплений из плоскости по растянутой от
момента М кромке, или при m < 4 коэффициент М по формуле
следует умножать на дополнительный коэффициент kжМ.
Значения kжМ приведены в табл. 2 прил. 4 СНиП ДК при m
4 kжМ = 1.
32.
Расчет изгибаемых элементовПроверку устойчивости плоской формы деформирования изгибаемых
элементов постоянного двутаврового или коробчатого поперечного сечений
следует производить в тех случаях, когда
lp 7b
,
где b - ширина сжатого пояса поперечного сечения.
Расчет следует производить по формуле:
σ
=
M
Rc
Wбр
,
где - коэффициент продольного изгиба из плоскости изгиба сжатого пояса
элемента, определяемый по п. 4.3;
Rс - расчетное сопротивление сжатию;
Wбр - момент сопротивления брутто поперечного сечения; в случае
фанерных стенок - приведенный момент сопротивления в плоскости изгиба
элемента.
33.
Расчет изгибаемых элементовРасчет изгибаемых элементов на прочность по скалыванию
следует выполнять по формуле:
τ =
QS бр
I брb расч
R ск
,
где
Q - расчетная поперечная сила;
S бр - статический момент брутто сдвигаемой части поперечного
сечения элемента относительно нейтральной оси;
Iбр - момент инерции брутто поперечного сечения элемента
относительно нейтральной оси;
bрас - расчетная ширина сечения элемента;
Rск - расчетное сопротивление скалыванию при изгибе.
34.
РАСЧЕТ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХКОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ
СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
Растянуто-изгибаемые и внецентреннорастянутые элементы
35.
Расчет растянуто-изгибаемых ивнецентренно-растянутых элементов
Работают одновременно на
растяжение и изгиб.
В сечениях растянуто-изгибаемого
элемента от продольной
растягивающей силы N возникают
равномерные растягивающие
напряжения, а от изгибающего
момента М – напряжения изгиба.
Эти напряжения суммируются,
благодаря чему растягивающие
напряжения увеличиваются, а
сжимающие уменьшаются.
36.
Расчет растянуто-изгибаемых ивнецентренно-растянутых элементов
Расчет внецентренно-растянутых и растянутоизгибаемых элементов следует производить по прочности с
учетом всех ослаблений по формуле:
σ
N
MR p
Rр
= F
WрасчR и
расч
,
где Wрасч - расчетный момент сопротивления поперечного
сечения;
Fрасч - площадь расчетного сечения нетто.
37.
РАСЧЕТ ЭЛЕМЕНТОВ ДЕРЕВЯННЫХКОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ
СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
Сжато-изгибаемые и
внецентренно-сжатые элементы
38.
Расчет сжато-изгибаемых ивнецентренно-сжатых элементов
Расчет на прочность внецентренно-сжатых и сжатоизгибаемых элементов следует производить по формуле:
σ =
N
Fрасч
MД
Wрасч
Rc
,
где Мд – изгибающий момент в расчетном сечении от
действия поперечных и продольных нагрузок, определяемый
из расчета по деформированной схеме.
39.
Расчет сжато-изгибаемых ивнецентренно-сжатых элементов
Расчет на устойчивость плоской формы деформирования сжатоизгибаемых элементов следует производить по формуле:
n
МД
N
1
σ=
R c Fбр М R и Wбр
,
где
Fбр - площадь брутто с максимальными размерами сечения
элемента на участке lp;
Wбр - см. п. 4.14 СП ДК;
n = 2 - для элементов без закрепления растянутой зоны из
плоскости деформирования и n = 1 для элементов, имеющих такие
закрепления;
- коэффициент продольного изгиба, определяемый по формуле
(8) для гибкости участка элемента расчетной длиной lp из плоскости
деформирования;
м - коэффициент, определяемый по формуле .
































 Construction
Construction








