Кривые и поверхности 2-го порядка

1.

9. Кривые и поверхности 2-го порядка
Геометрические образы 1-го
порядка (прямая и плоскость)
прямая
Геометрические образы 2-го
порядка (прямая и плоскость)
эллипс, гипербола, парабола
эллиптический, гиперболический
и параболический цилиндры
плоскость
эллипсоид, сфера, однополостный
и двуполостный гиперболоиды
конус, эллиптический и
гиперболический параболоиды
описываются уравнениями
1-го порядка:
Ax + By + C = 0
Ax + By + Cz + D = 0
описываются уравнениями
2-го порядка:
a11x2 + 2a12xy + a22y2 +
+ 2b1x + 2b2y + c = 0

2.

9.1 Кривые второго порядка
9.1.1. Эллипс
Эллипс — ГМТ плоскости, сумма расстояний от которых до
двух фиксированных точек F1 и F2 постоянна и равная 2a
(2a>|F1F2|).
M ( x, y )
F1 и F2 — фокусы эллипса.
F1
O
F1(–c;0)
F2
и
F2(c;0)
|OF1| = |OF2| = c.
| F1M | | F2 M | 2a
фокальное свойство эллипса
фокальные радиусы
| ( x c, y ) | | ( x c, y ) | 2a

3.

| F1M | | F2 M | 2a
Вывод уравнения
( x c ) 2 y 2 ( x c ) 2 y 2 2a
( x c ) y 2a ( x c ) y
2
2
2
2
|
2
( x c ) 2 y 2 4a 2 4a ( x c ) 2 y 2 ( x c ) 2 y 2
4a ( x c) y 4a 4cx
2
cx
2
2
( x c) y a
a
2
cx
2
2
2
2
x 2 xc c y a 2cx
a
2
2
2
2
2
a
c
y
x
2
2
2
2
2
2
2
x
y
a
c
1
,
c
a
b
2
a
a 2 b2
2
2

4.

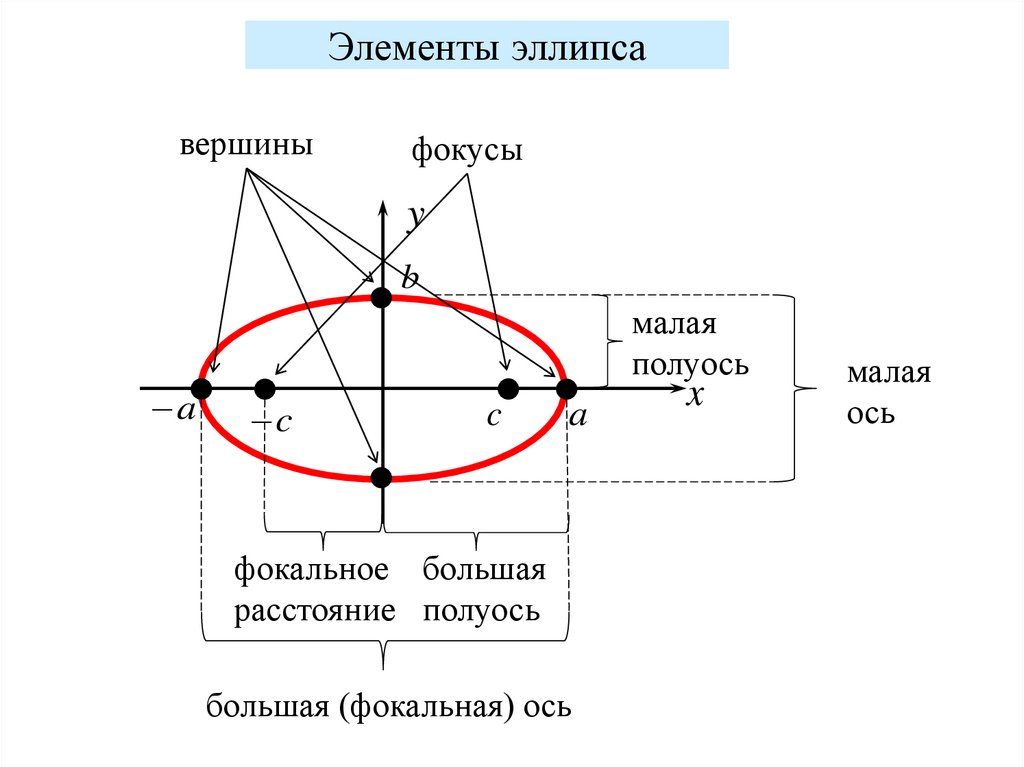
Элементы эллипса
вершины
фокусы
y
b
малая
полуось
a
c
c
a
фокальное большая
расстояние полуось
большая (фокальная) ось
x
малая
ось

5.

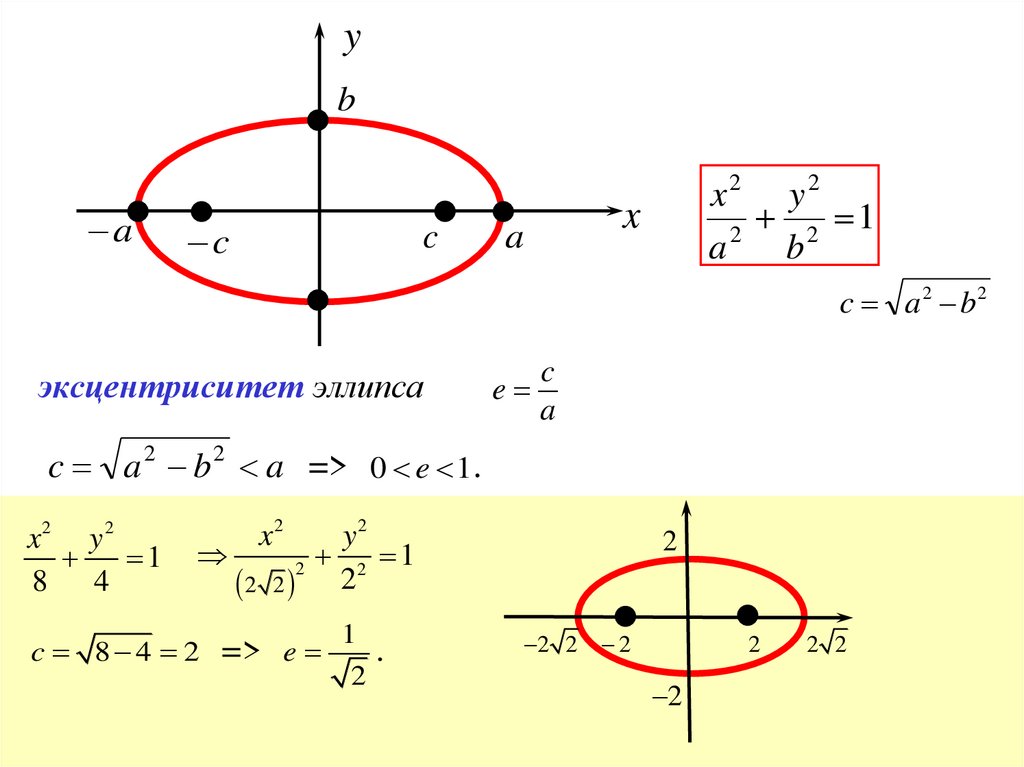
y
b
a
c
c
x2 y2
2 1
2
a
b
x
a
c a 2 b2
эксцентриситет эллипса
e
c
a
c a 2 b 2 a => 0 e 1.
x2 y 2
1
8
4
x2
y2
2 1
2
2 2 2
1
c 8 4 2 => e
.
2
2
2 2
2
2
2
2 2

6.

( x x0 )2 ( y y0 ) 2
1 уравнение со смещенным центром
2
2
a
b
x 1
2
8
y 3
4
2
1
1
2
3
2 2
2
2
2
x 1
4
2
y 3
8
2
1
- большая и малая оси
меняются местами
2 2

7.

4 x 2 24 x y 2 6 y 4 0
Приведение к каноническому виду
2 x 2 6 2 x 62 y 2 2 3 y 32 36 9 4 0
2
2 x 6 y 3
2
4 x 3
2
49
x 3
3,5
2
y 3
7
2
2
2
49
2
y 3
2
1
49
y 3
7
2
1
2
x 3
3,5
2
2
1
Параметрические уравнения эллипса
x a cos t
y b sin t

8.

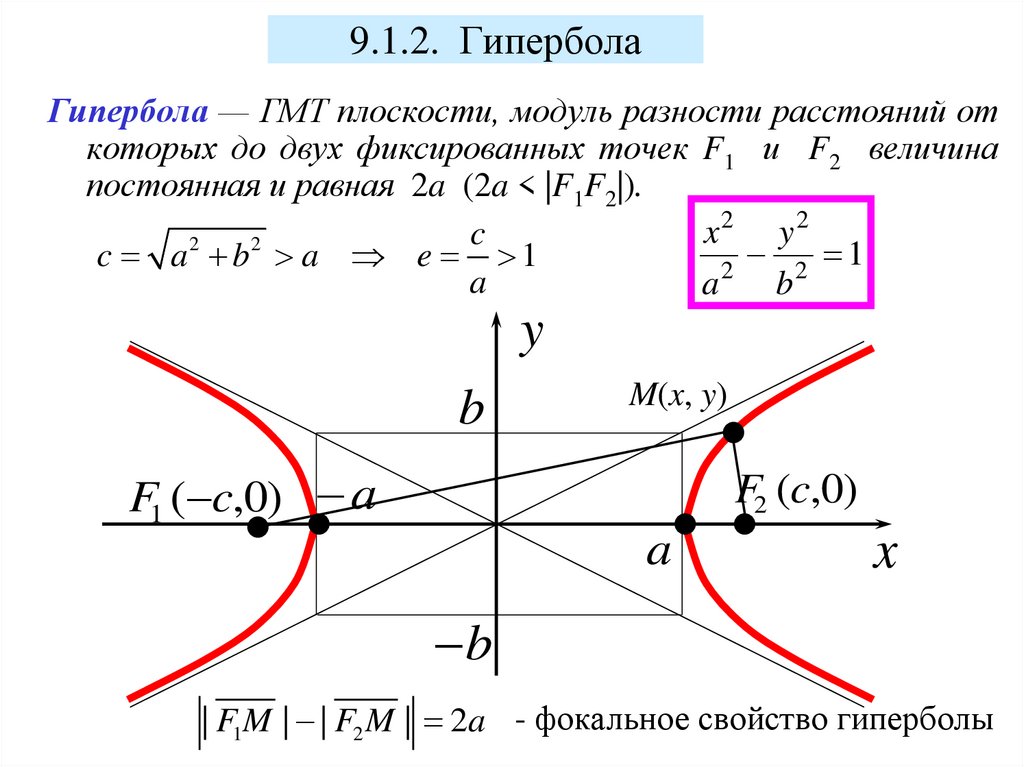
9.1.2. Гипербола
Гипербола — ГМТ плоскости, модуль разности расстояний от
которых до двух фиксированных точек F1 и F2 величина
постоянная и равная 2a (2a < |F1F2|).
2
2
x
y
c
2 1
c a 2 b2 a e 1
2
a
a
b
y
b
M(x, y)
F1 ( c,0) a
F2 (c,0)
a
x
b
| F1M | | F2 M | 2a - фокальное свойство гиперболы

9.

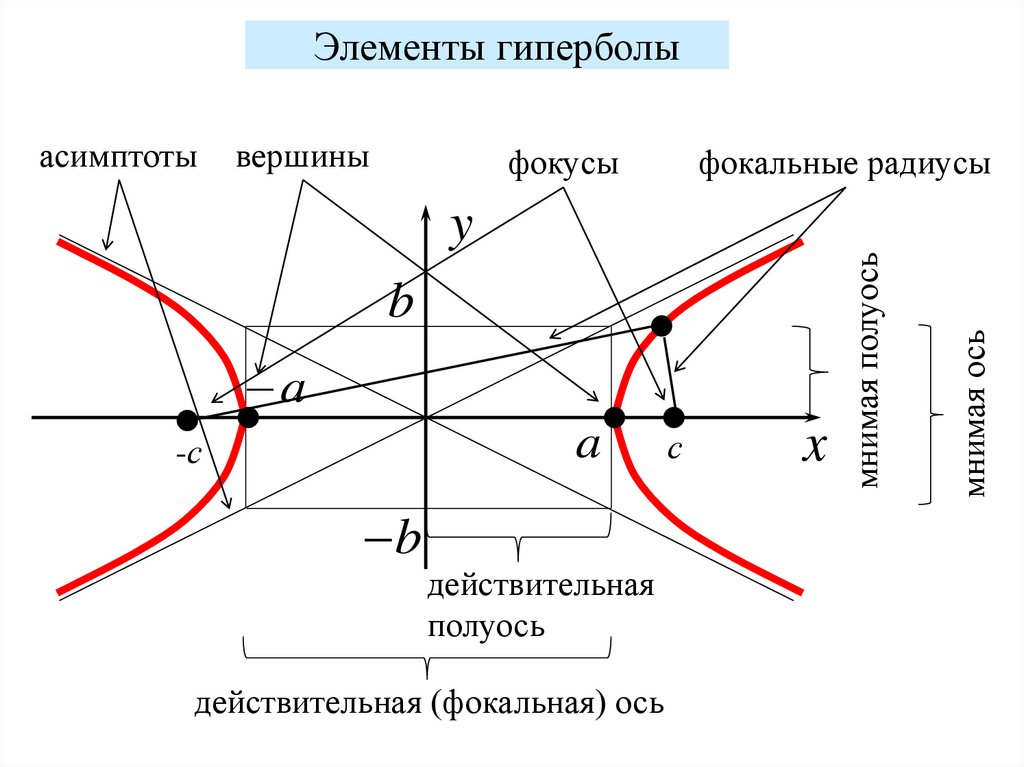
Элементы гиперболы
асимптоты
вершины
фокусы
фокальные радиусы
a
a
-с
b
действительная
полуось
действительная (фокальная) ось
с
x
мнимая ось
b
мнимая полуось
y

10.

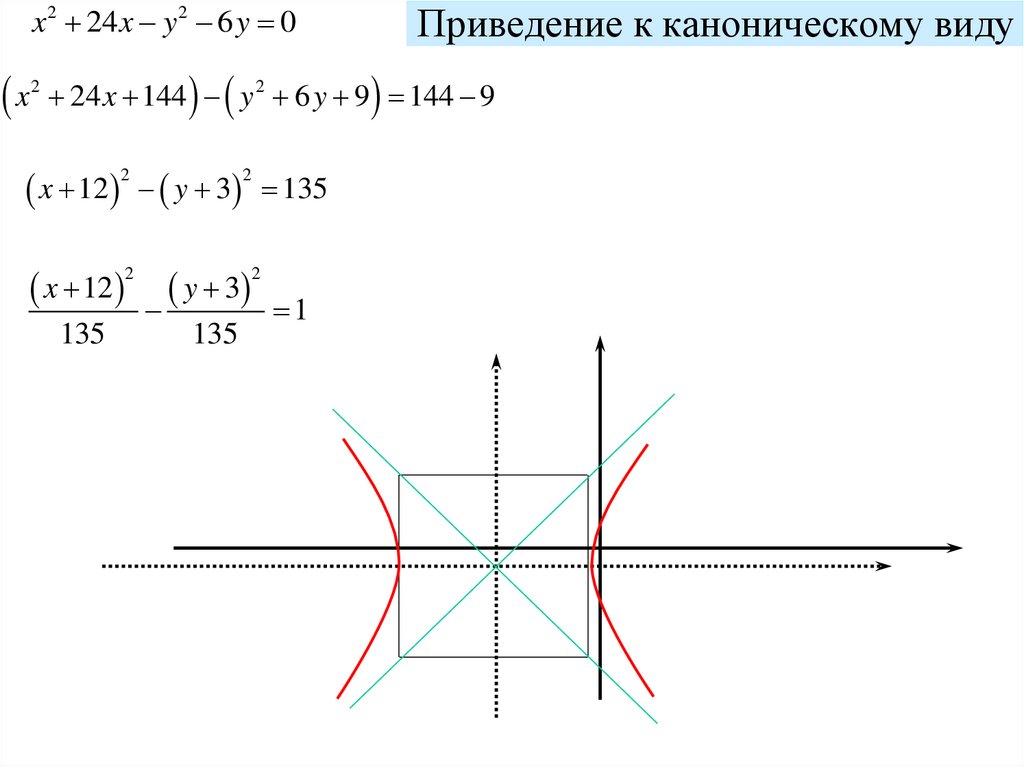
x 2 24 x y 2 6 y 0
x
2
Приведение к каноническому виду
24 x 144 y 2 6 y 9 144 9
x 12 y 3
2
x 12
135
2
y 3
135
135
2
2
1

11.

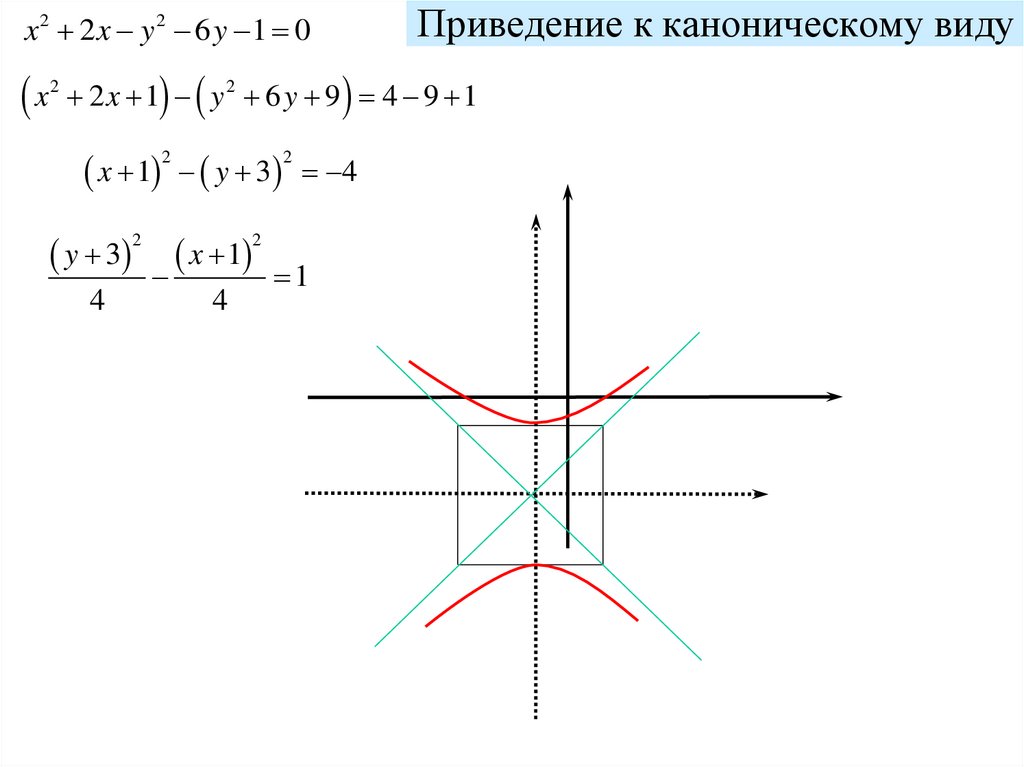
x2 2x y 2 6 y 1 0
x
2
Приведение к каноническому виду
2 x 1 y 2 6 y 9 4 9 1
x 1 y 3
2
y 3
4
2
x 1
4
2
4
2
1

12.

9.1.3. Парабола
Парабола — ГМТ плоскости, расстояние от которых до
фиксированной прямой d и до фиксированной точки F (не
лежащей на прямой d) одинаково.
F — фокус параболы, d – директриса.
A
y2 = 2px или x = ay2
d
M
y
d
p
F
O F
x
|AM| = |FM| - фокальное
свойство параболы

13.

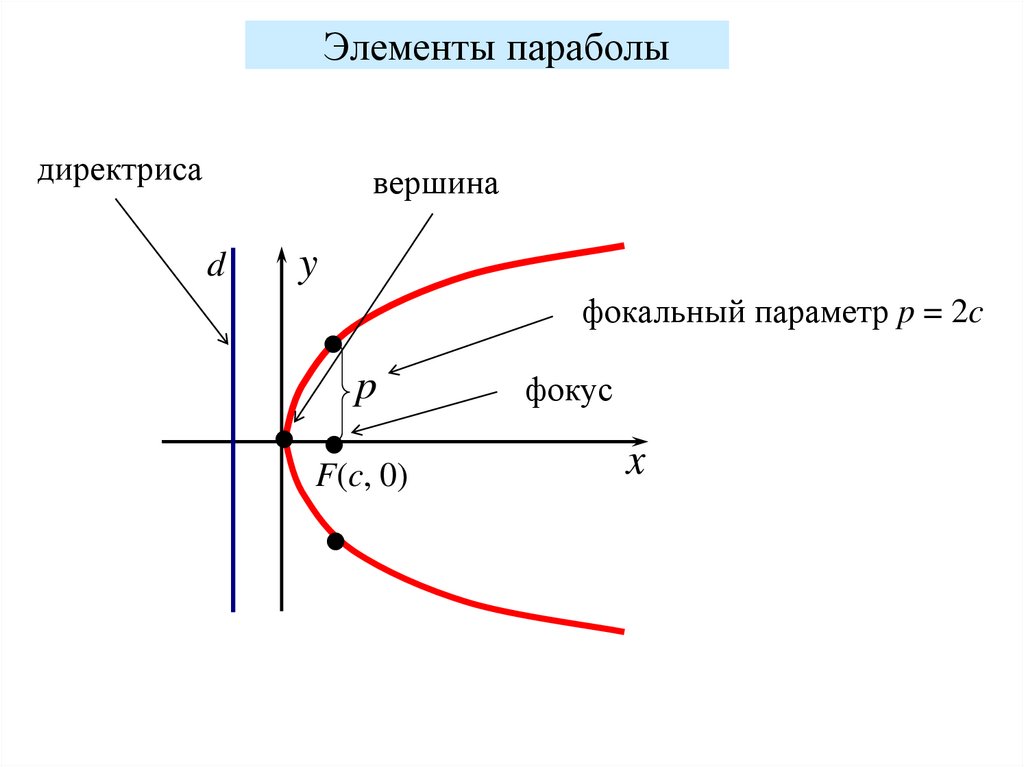
Элементы параболы
директриса
вершина
d
y
фокальный параметр p = 2c
p
F(c, 0)
фокус
x

14. 9.1.4. Общее определение эллипса, гиперболы и параболы

a
— директрисы эллипса и гиперболы
e
M – произвольная точка кривой.
ri = | MFi | — расстояние до фокуса,
ρi = ρ(M,di) — расстояние до директрисы
d1, 2 : x
ТЕОРЕМА.
Для любой точки эллипса, гиперболы
или параболы имеет место равенство
ri
i
e
ГМТ, для которых отношение расстояния до фокуса к расстоянию
до директрисы постоянно и равно e, называется
1) эллипсом, при e<1 ;
2) гиперболой, при e>1;
3) параболой, при e = 1.

15.

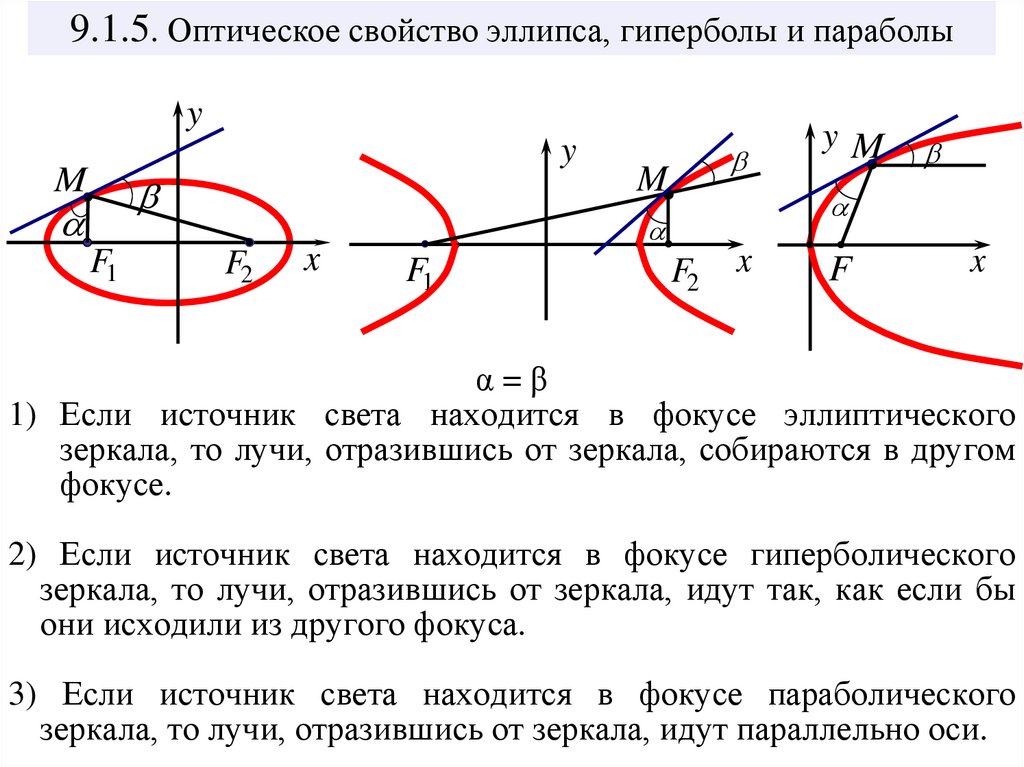
9.1.5. Оптическое свойство эллипса, гиперболы и параболы
y
y
M
F1
F2
x
M
F1
yM
F2
x
F
x
α=β
1) Если источник света находится в фокусе эллиптического
зеркала, то лучи, отразившись от зеркала, собираются в другом
фокусе.
2) Если источник света находится в фокусе гиперболического
зеркала, то лучи, отразившись от зеркала, идут так, как если бы
они исходили из другого фокуса.
3) Если источник света находится в фокусе параболического
зеркала, то лучи, отразившись от зеркала, идут параллельно оси.