Similar presentations:
Графическое отображение технических форм. Вопросы для самоконтроля и задачи
1.
Вопросы для самоконтроля и задачи для самостоятельной работы потеме "Графическое отображение технических форм"
у
с
т
н
о
1.1. Какой вид проецирования используется при построении машиностроительных
чертежей?
1.2. Что такое проекция точки?
1.3. Что означает “обратимость” изображений?
1.4. Какие основные плоскости проекций вы знаете, их расположение в пространстве?
Что называется осью проекций?
1.5. Что такое двухкартинный чертеж точки?
1.6. Что называется линиями проекционной связи и как они располагаются на чертеже по
отношению к осям проекций?
1.7. Что такое координата точки?
1.8. Какими координатами определяется расстояние от точки до плоскости проекций П 1,
П2, П3?
1.9. Какими координатами определяется горизонтальная проекция точки А – А1….;
фронтальная – А2 … ; профильная – А3 ... ?
1.10. Запишите условие принадлежности точки А, связав его с координатами этой точки:
Тема 1
горизонтальной плоскости проекций … ; фронтальной ….; профильной …. .
15
1.11. Запишите условие принадлежности точки А, связав его с координатами этой точки:
оси 0x –
; 0y –
; Oz –
.
1.12. Постройте на трехкартинном чертеже три проекции точек А, В, С, запишите их
координаты и заполните таблицу.
z
z
A ... , ... , ...
B ... , ... , ...
C ... , ... , ...
A
B
П2
П3
0
x
C
x
y
П1
Обозн ачен и е
П1
П2
П3
x, y, z
А1
А2
А3
А 1А 2
А 1А 3
0
y
Назван и е элемен тов чертеж а
1.13. На наглядном изображении построить проекции А2, С1 и D2 точек А, С, D и выполнить
двухкартинный чертеж этих точек.
2.
четверти.1.16. Построить недостающие проекции
точек А,В,С и D.
1.15. К какой из плоскостей проекций
– П1, П2 или П3 – точка А находится
ближе? – К …
z
A2
z
A3
A2
D2
x
0
D3
B2
B3
A1
y
C2 = C1
x
0
A1
y
1.17. Построить недостающие оси проекций.
z
A2
A3
а)
б)
A2
A3
x
A1
A1
1.18. Какой из плоскостей проекций – П1, П2, П3 – принадлежит точка A, координаты
которой 20, 30, 0? . . .
1.19. От какой из плоскостей проекций – П1, П2, П3 – точка A (30, 40, 50) находится
дальше
. . . , ближе . . . ?
1.20. Укажите положение в пространстве точки A с координатами 20, 0, 0 . . . .
17
Тема 1
3.
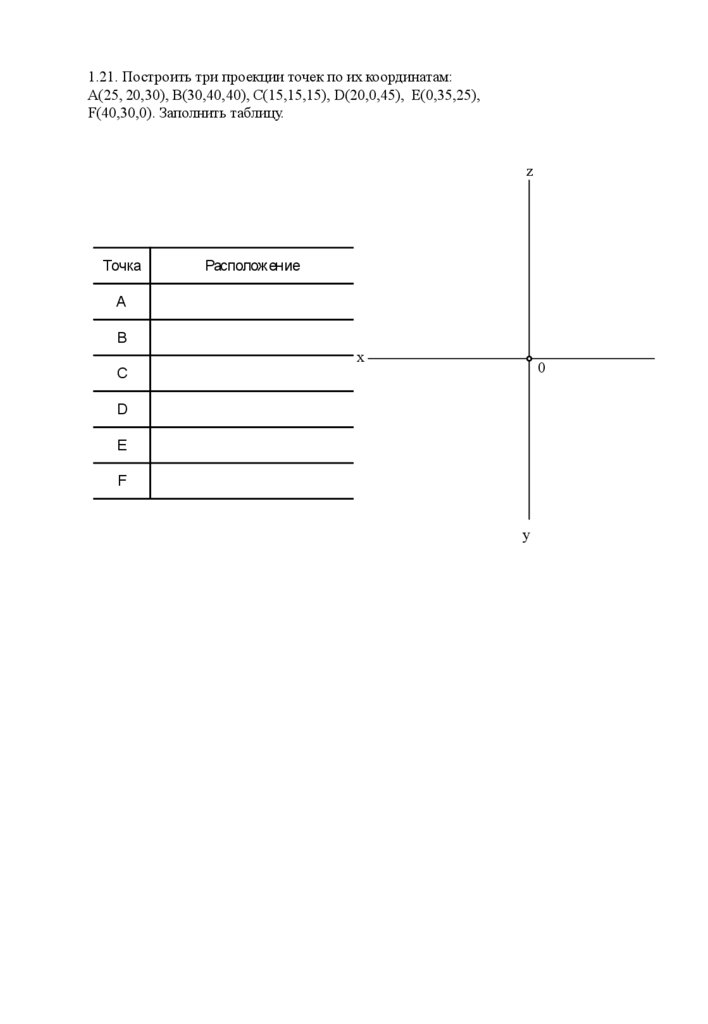
1.21. Построить три проекции точек по их координатам:А(25, 20,30), В(30,40,40), С(15,15,15), D(20,0,45), E(0,35,25),
F(40,30,0). Заполнить таблицу.
z
Точка
Расположение
A
B
x
0
C
D
E
F
y
Тест (Тема 1)
1.1. Как называется (а, б, в) плоскость проекций П2?
а) горизонтальная
б) фронтальная
в) профильная
1.2. Как называется (а, б, в) линия А2А1?
а) ось проекций б) вертикальная линия связи в) горизонтальная линия связи
1.3. Какая точка (рис.1) лежит в горизонтальной плоскости проекций?
1.4. Какая из точек (A, B, C, D) рис. 1 наиболее удалена от
горизонтальной плоскости проекций?
1.5. Широта какой точки (A, B, C, D) рис.1 равна 0?
1.6. Для какой из точек (A, B, C, D) глубина (рис.1)
равна 7 мм?
1.7. На сколько мм точка В (рис.1) удалена от плоскости П2 дальше, чем точка А?
Рис.1
1.8. Какая координата (x, y, z) точки А (рис.1) имеет
меньшее числовое значение?
1.9. Какие координаты (а, б, в) определяют точку, лежащую в плоскости П 2?
а) x, z
б) x, y
в) y, z
1.10. Какая из точек (а, б, в) лежит в горизонтальной плоскости проекций?
а) А (10, 15, 0) б) B (15, 0, 20) в) C (10, 15, 20)
Тема 1
18
4.
Вопросы для самоконтроля и задачидля самостоятельной работы по теме
"Образование линии в пространстве и задание ее на чертеже"
у
с
т
н
о
2.1. Какие линии вы знаете: по их виду, по расположению относительно плоскости?
2.2. В чем различие между плоской и пространственной линиями?
2.3. Чем может быть задана прямая линия в пространстве и на чертеже?
2.4. Какое положение может занимать прямая относительно плоскостей проекций?
2.5. Какие линии уровня вы знаете? Как располагаются их проекции на чертеже?
2.6. Какие проецирующие прямые вы знаете?
2.7. Что называется следом прямой? Г де расположены горизонтальная проекция
фронтального следа и фронтальная проекция горизонтального следа?
2.8. Назовите признак параллельных прямых на чертеже, пересекающихся и
скрещивающихся.
2.9. Назовите примеры плоских кривых линий.
2.10. Назовите пример пространственной кривой.
2.11. Охарактеризуйте положение каждой стороны треугольника АВС относительно
плоскостей проекций и сделайте запись в таблице (см. отрезок АВ).
A2
B2
Отрезок
AB
Название прямых
профильно-проецирующая прямая
BC
x
CA
C2
A1
B1
A2
C1
2.12. Как расположены относительно плоскостей
проекций прямые b, с?
а П3
b .....
с .......
c2
a2
b2
a1
b1
B2
x
A1
c1
B1
Тема 2
26
5.
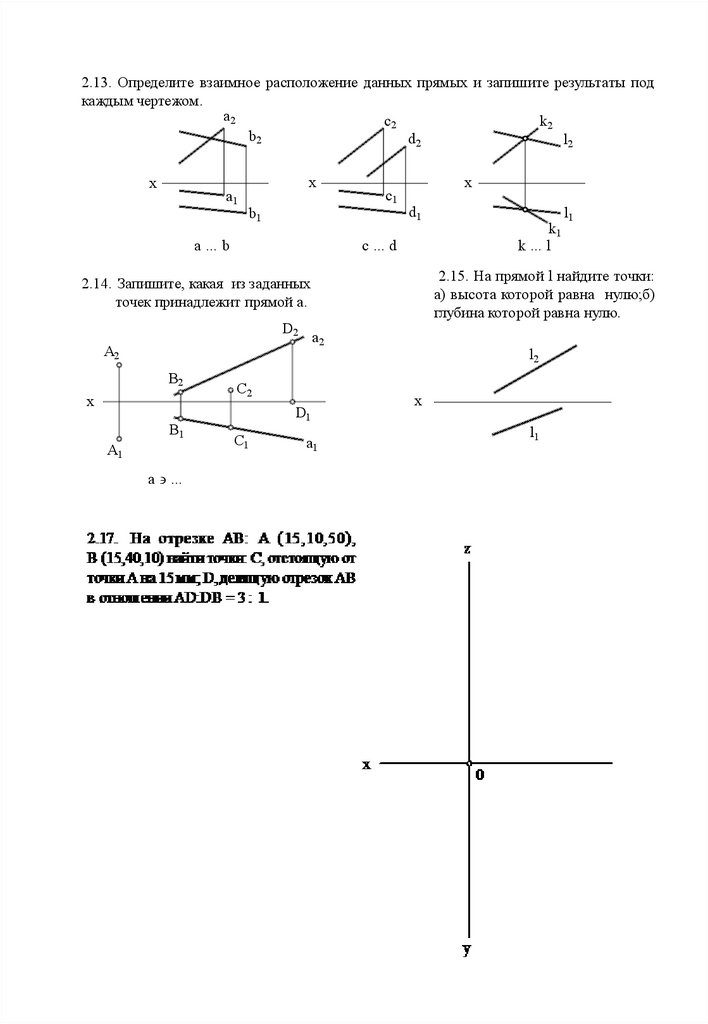
2.13. Определите взаимное расположение данных прямых и запишите результаты подкаждым чертежом.
a2
c2
k2
b2
d2
l2
x
a1
x
c1
b1
a ... b
x
d1
c ... d
D2
a2
A2
l2
C2
x
x
D1
B1
C1
A1
l1
2.15. На прямой l найдите точки:
а) высота которой равна нулю;б)
глубина которой равна нулю.
2.14. Запишите, какая из заданных
точек принадлежит прямой а.
B2
k1
k ... l
l1
a1
a ...
2.16. Впишите в таблицу названия изображенных линий; укажите, какие из них являются
кривыми второго порядка (см. чертеж д).
а)
б)
в)
г)
Чертеж
д)
2-го порядка(да,нет)
Название линии
а
б
в
г
д
Парабола
Да
Тема 2
27
6.
7.
8.
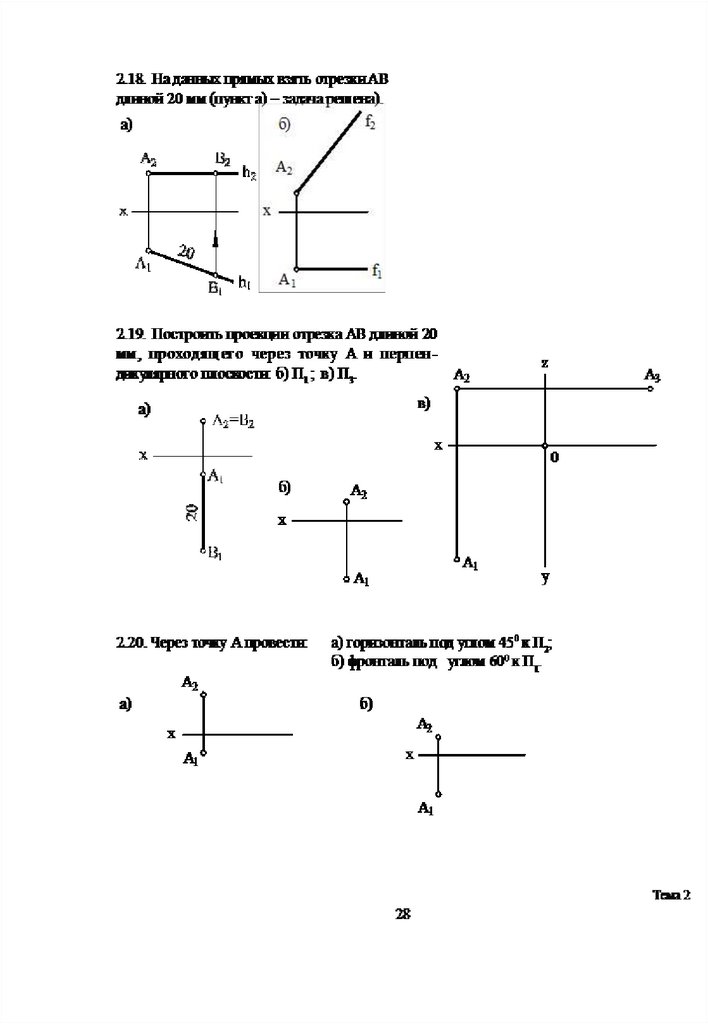
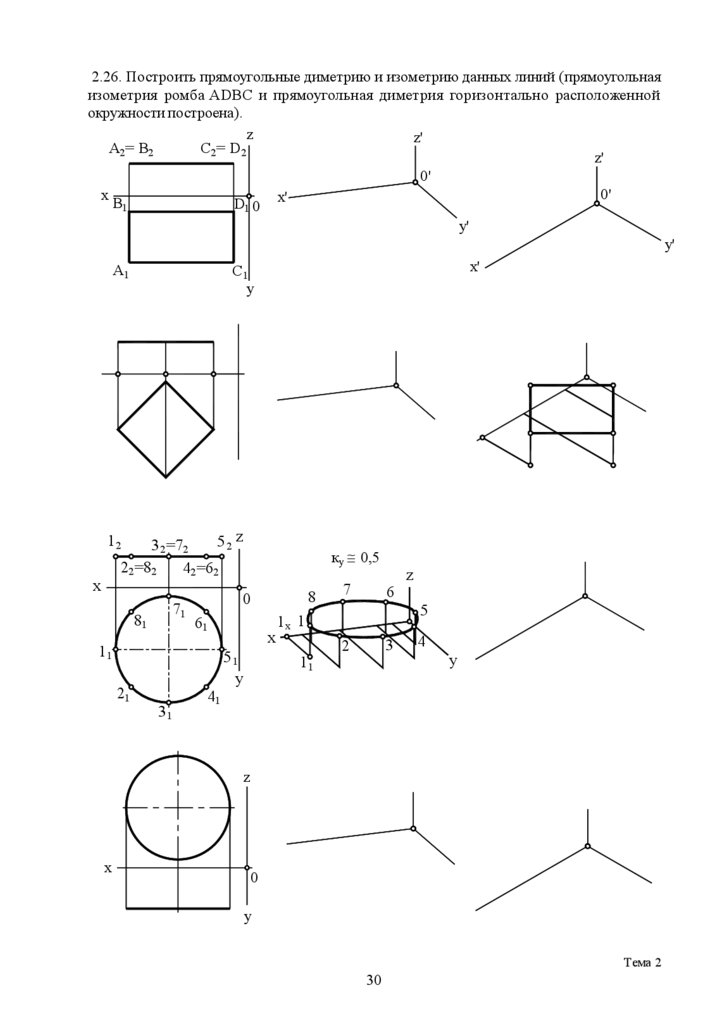
2.26. Построить прямоугольные диметрию и изометрию данных линий (прямоугольнаяизометрия ромба ADBC и прямоугольная диметрия горизонтально расположенной
окружности построена).
z
z'
A2= B2
C2= D2
z'
0'
0'
x
B1
D1 0 x'
y'
y'
A1
x'
C1
y
52 z
3 2 =72
22 =82
42 =62
12
x
71
81
61
x
51
y
31
8
0
11
21
кy 0,5
7
6
5
1x 1
11
z
3
2
4
y
41
z
x
0
y
Тема 2
30
9.
ус
т
н
о
3.3.
Каковыдля
особенности
изображения
на чертеже
уровня и проецирующей
Вопросы
самоконтроля
и задачи
для плоскости
самостоятельной
работы по
плоскости?
теме "Формирование поверхности в пространстве и задание ее
3.4. Каким свойством обладает вырожденная проекция плоскости (проекция-носитель)?
определителя
нарасположены
чертеже"
3.3. Что
Каковы
особенности
изображения
чертеже
плоскости
уровня и проецирующей
3.5.
называется
следом
плоскости?наГде
горизонтальная
проекция
плоскости? следа и фронтальная проекция горизонтального следа?
фронтального
3.1.
элементами
можетточки
быть плоскости.
задана плоскость
пространстве
и на чертеже?
3.4. Какими
Каким свойством
обладает
вырожденная
проекция вплоскости
(проекция-носитель)?
3.6.
Условие
принадлежности
3.2.
Как
могут
располагаться
плоскости
по
отношению
к
плоскостям
проекций
и как
3.5. Условие
Что называется
следом плоскости?
Где расположены горизонтальная
проекция
3.7.
принадлежности
прямой плоскости.
они
называются?
фронтального
следаназываются
и фронтальная
проекция
горизонтального
следа?
3.8.
Какие прямые
главными
(особыми)
линиями плоскости?
Тема 3
3.3.
на чертеже
плоскости
уровня
и проецирующей
3.6. Каковы
Условие
принадлежности
плоскости.
3.9.
На
какихособенности
чертежах а, изображения
б, в, г,точки
д заданные
элементы
определяют
плоскость?
плоскости?
3.7. Условие принадлежности прямой плоскости.
39
3.4.
обладает вырожденная
проекциялиниями
плоскости
(проекция-носитель)?
3.8. Каким
Какие свойством
прямые называются
главными (особыми)
плоскости?
3.5.
называется
следом
плоскости?
Гдеэлементы
расположены
горизонтальная
3.9. Что
На каких
чертежах
а, б, в,
г, д заданные
определяют
плоскость?проекция
фронтального следа и фронтальная проекция горизонтального следа?
3.6. Условие принадлежности точки плоскости.
3.7. Условие принадлежности прямой плоскости.
B2
3.8. Какие прямые называются главными (особыми) линиями
плоскости?
c2
3.9. На каких
чертежах
а,
б,
в,
г,
д
заданные
элементы
определяют
плоскость?
b2
d2
B
2
A2
a2
C2
c2
b2
d2
x
x
x
x
A2
a2
C1
C2
B1
d1
b1
A1
B
2
c
x
x
x
x
1
г)
a1
c2 c2 d
C1
b2
d2d12
B
1
а)
б)
b1
A1в)
c
A2
a2
1
г)
a1
C2
c2 d
x
2
Чертежи
аx
бб) в
г
дx
x а)
x
в)
Да, нет
C1
B1
c1 d1d1
b
x д)
c
Чертежи 1 а
б
в
г
д A1
1
г)
a
Да, 1нет
c2 d
2
c1 d1
а)
б)
в)
д)
x
Чертежи
а
б
в
г
д
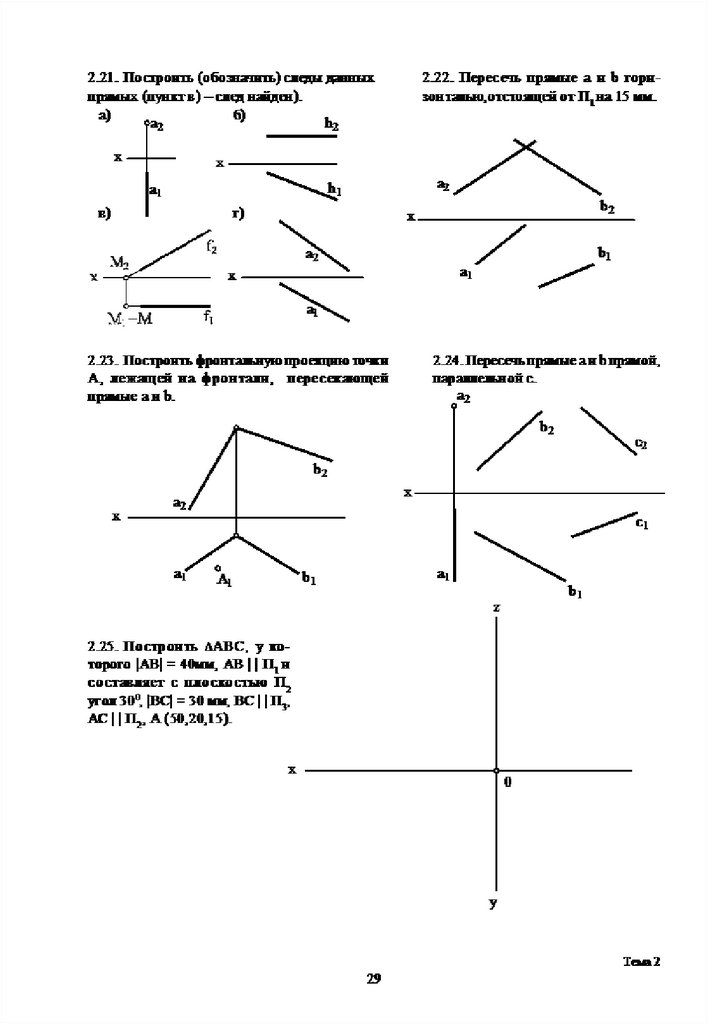
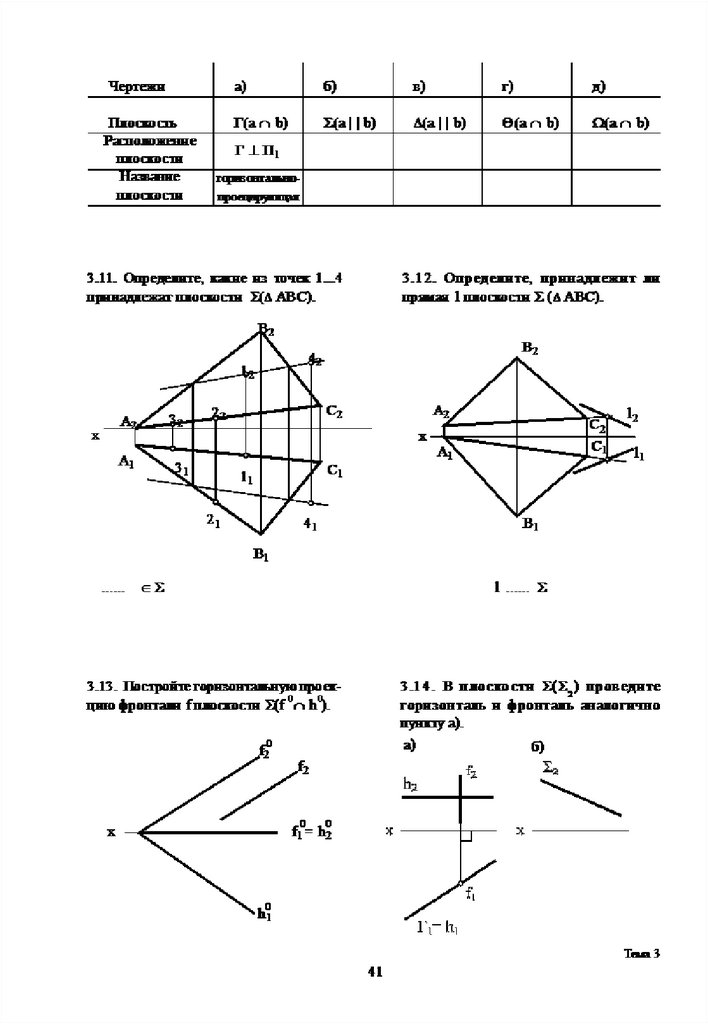
3.10. Определите расположение плоскостей относительно плоскостей
Да, нет
проекций, заполните таблицу (см. пункт а).
c1 d1
д)
3.10. Определите
относительно
плоскостей
a2
a2=b2
b2
b2 расположение плоскостей
a2
проекций, заполните таблицу (см. пункт а).
a2
b2
a2=b2
a2
a2=b2
b2
b2
x
x
x
x
x a2
a2 Определите расположение
ab12
3.10.
относительно плоскостей
a2=b2 a1 плоскостей
b1
проекций, заполните таблицу (см.
a1
b1
b1 пункт а).
x
x
x
x b1
x a1
a1=b1
a1
а)
б)
г)
д)2
aa21 в)
a2=b
b2
b2
a2
b
a
b
b1
1
1
Тема1 3
a1
a2
bb2 1
a2=b2
40
a1=b1
а)
б)
в)
г)
д)
x
x
x
x
x
Тема 3
a1
a1
40
b
10.
11.
12.
Вопросы для самоконтроля и задачи по теме "Формированиеповерхностей вращения, линейчатых поверхностей в пространстве и
задание их на чертеже"
у
с
т
н
о
4.3.
точки и линии
поверхности?
4.1. Каковы
В чем условия
состоит принадлежности
сущность кинематического
способа
образования поверхностей?
4.4.
Как
образуются
линейчатые
развертываемые
поверхности?
Приведите
примеры.
4.2. Что такое “определитель поверхности”, из чего состоит (его
составные
части, что
4.5.
Как
образуются
линейчатые
поверхности
с
плоскостью
параллелизма?
Назовите
их.
он в себя включает)?
4.6.
Как
образуются
поверхности
вращения?
Приведите
примеры.
Тема 4
4.3. Каковы условия принадлежности точки и линии поверхности?
4.7.
Какие
поверхности
называются
винтовыми?
4.4. Как образуются линейчатые развертываемые
поверхности? Приведите примеры.
52
4.8.
каждуюлинейчатые
из данныхповерхности
поверхностей
( а ... з) и параллелизма?
постройте недостающие
4.5. Назовите
Как образуются
с плоскостью
Назовите их.
проекции
точек,
принадлежащих
им.
(См.
пункт
а).
4.6. Как образуются поверхности вращения? Приведите примеры.
4.7. Какие поверхности называются винтовыми?
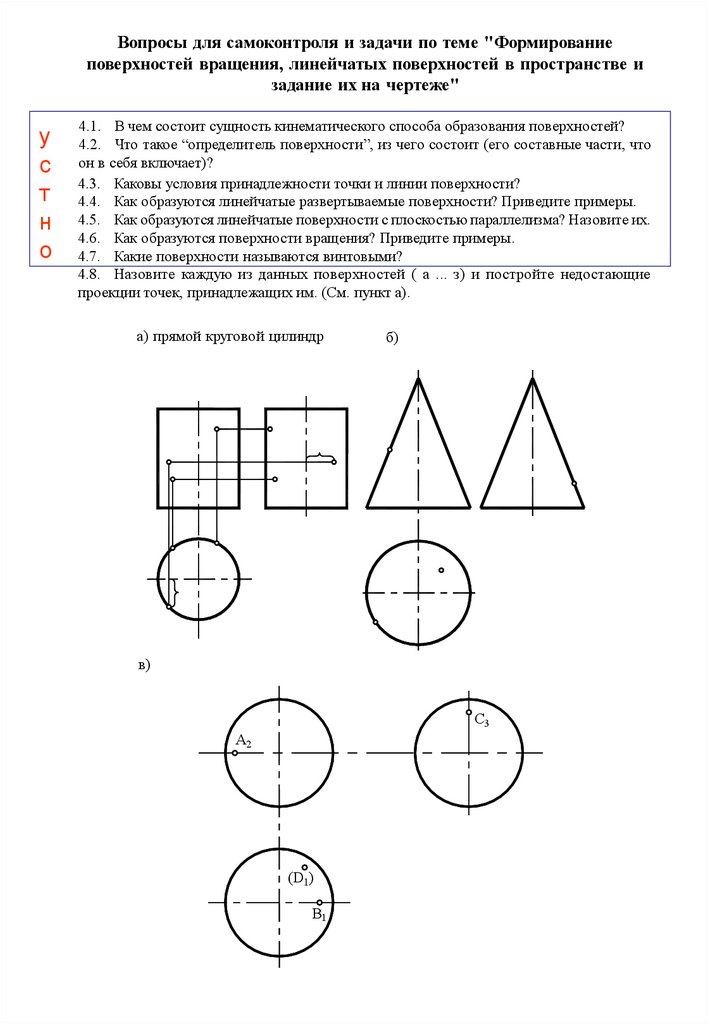
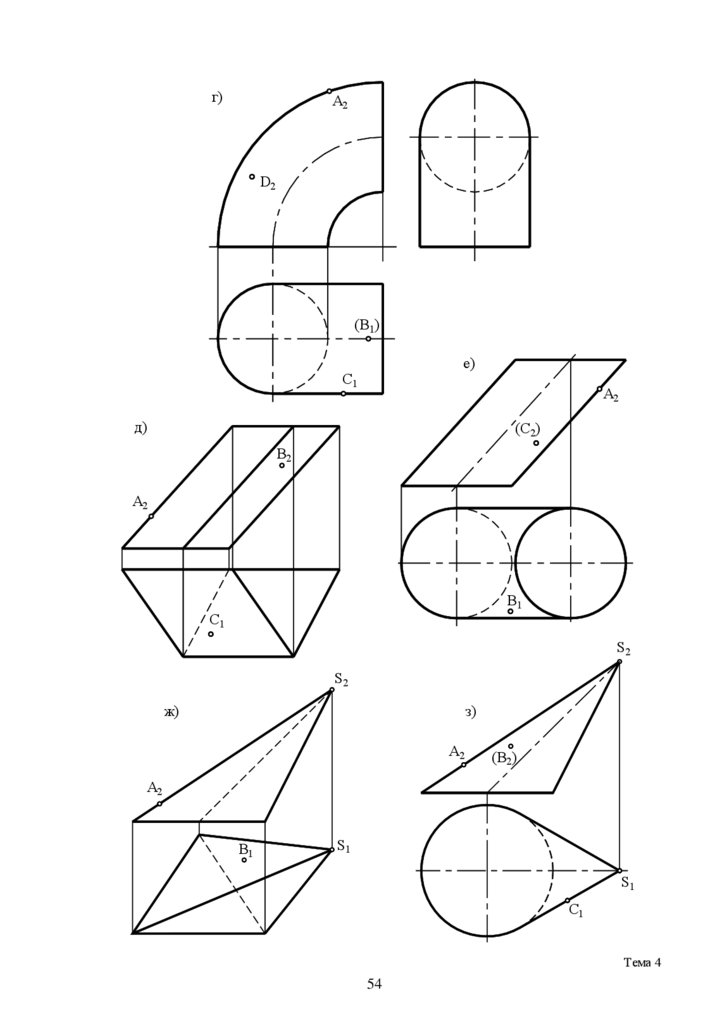
4.8. Назовите
каждую
из цилиндр
данных поверхностей
( а ... з) и постройте недостающие
а) прямой
круговой
б)
проекции точек, принадлежащих им. (См. пункт а).
а) прямой круговой цилиндр
б)
в)
в)
C3
A2
C3
A2
(D1)
B1
(D1)
B1
Тема 4
13.
г)A2
D2
(B1)
е)
C1
A2
д)
(C2)
B2
A2
B1
C1
S2
S2
ж)
з)
A2
(B2)
A2
B1
S1
S1
C1
Тема 4
54
14.
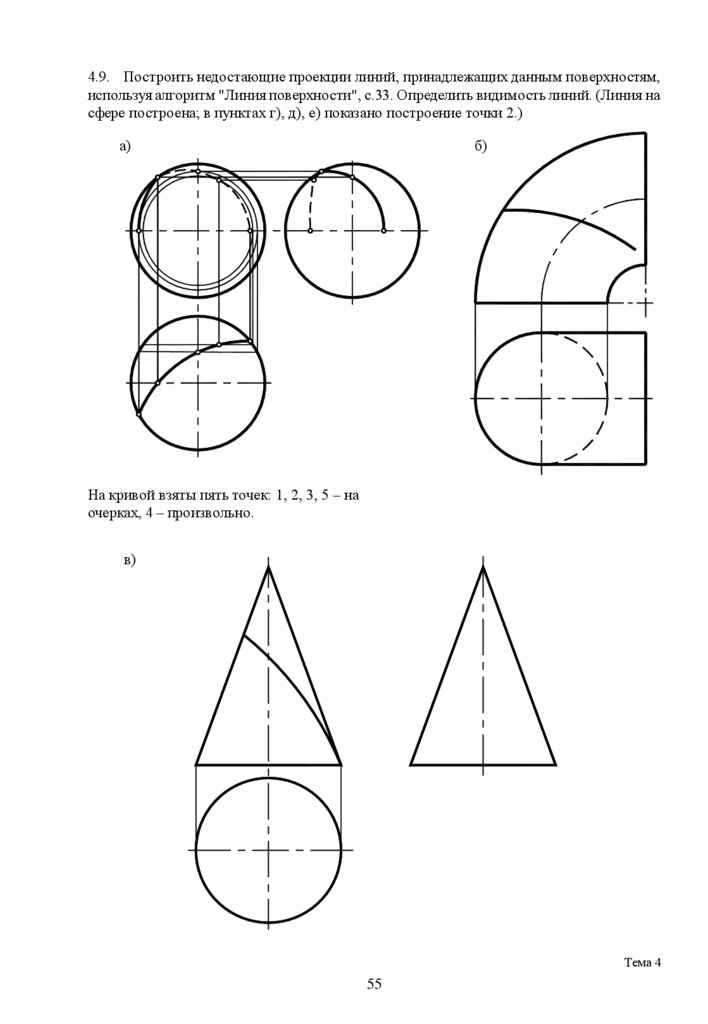
4.9. Построить недостающие проекции линий, принадлежащих данным поверхностям,используя алгоритм "Линия поверхности", с.33. Определить видимость линий. (Линия на
сфере построена; в пунктах г), д), е) показано построение точки 2.)
а)
б)
На кривой взяты пять точек: 1, 2, 3, 5 – на
очерках, 4 – произвольно.
в)
Тема 4
55
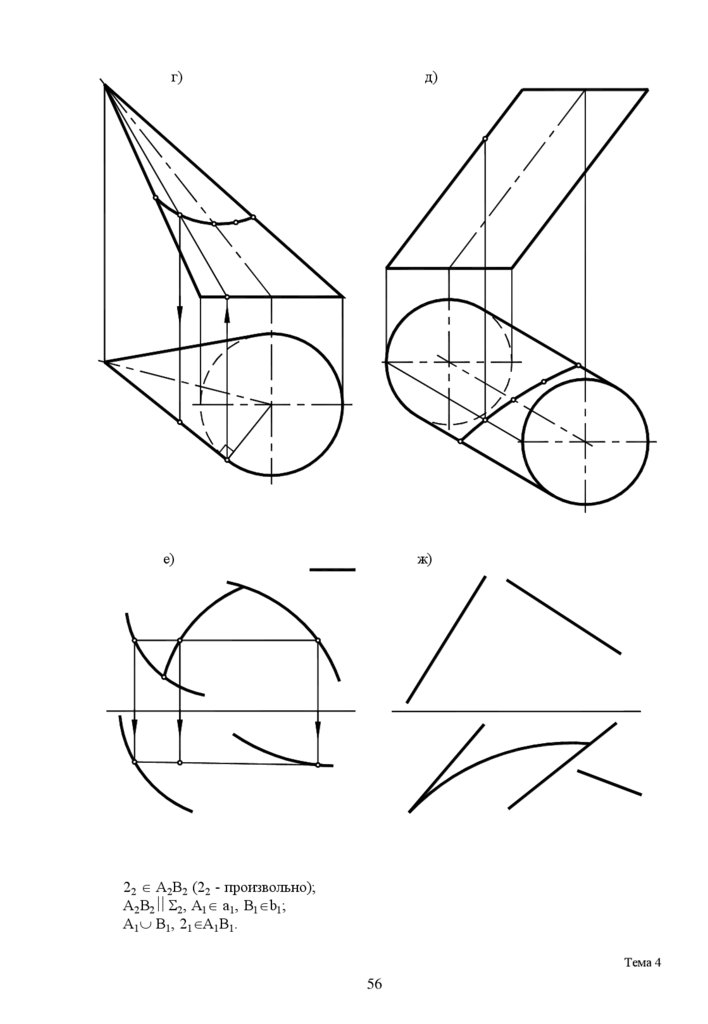
15.
г)д)
е)
ж)
22 A2B2 (22 - произвольно);
А2В2 2, А1 a1, B1 b1;
A1 B1, 21 A1B1.
Тема 4
56
16.
Вопросы для самоконтроля и задачи для самостоятельной работы потеме "Пересечение проецирующего геометрического образа с
геометрическим образом частного и общего положения"
у
с
т
н
о
5.1. Какие поверхности называются проецирующими?
5.2. Каким свойством обладает проекция-носитель поверхности?
5.3. К чему сводится определение проекций общего элемента двух проецирующих геометрических образов?
5.4. К чему сводится определение проекций общего элемента проецирующего образа и
геометрического образа общего положения?
5.5. Какие точки называются опорными?
5.6. Какая линия получается в сечении сферы плоскостью?
5.7. Как следует расположить секущую плоскость по отношению к оси цилиндра вращения,
чтобы получить: две прямые, окружность, эллипс?
5.8. Как располагается секущая плоскость, дающая в сечении конуса вращения: две прямые,
эллипс, параболу, гиперболу?
5.9. Найдите и обозначьте проекции общего элемента данных геометрических образов.
а)
l2
б)
C2
l2
B2
A2
2
x
1
A1
C1
l1
l1
B1
в)
г)
2
2
2
1
2
1
Тема 5
65
17.
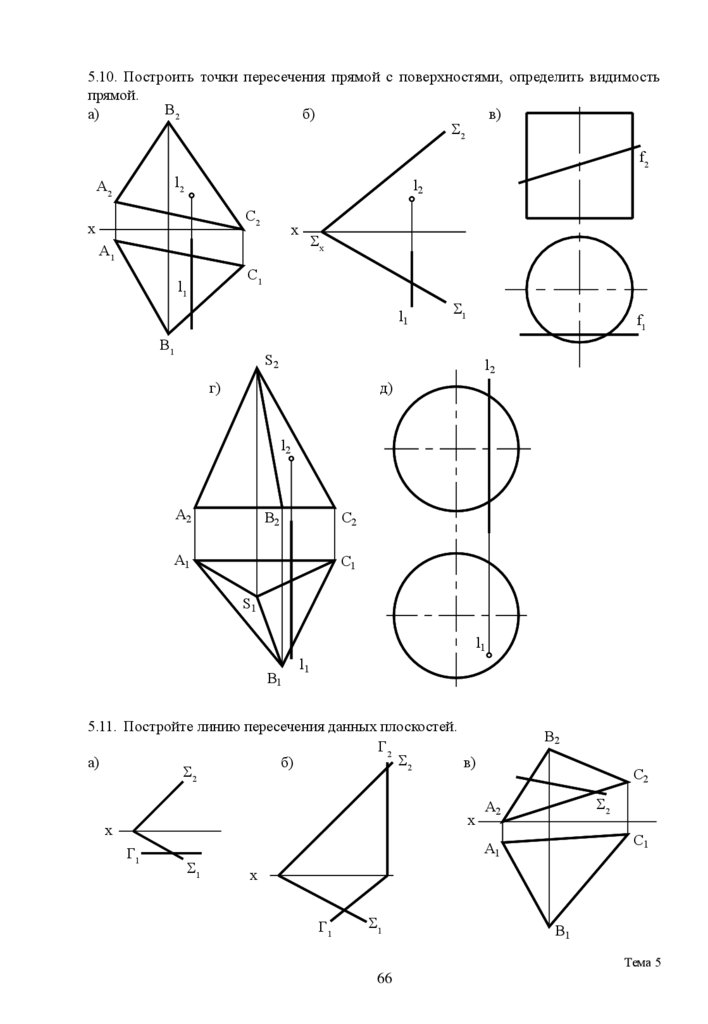
5.10. Построить точки пересечения прямой с поверхностями, определить видимостьпрямой.
B2
а)
б)
в)
2
f2
l2
A2
l2
C2
x
x
x
A1
C1
l1
l1
B1
1
f1
S2
l2
г)
д)
l2
A2
B2
C2
A1
C1
S1
l1
B1
l1
5.11. Постройте линию пересечения данных плоскостей.
2
2
а)
б)
в)
2
x
x
1
1
B2
C2
2
A2
C1
A1
x
1
1
B1
Тема 5
66
18.
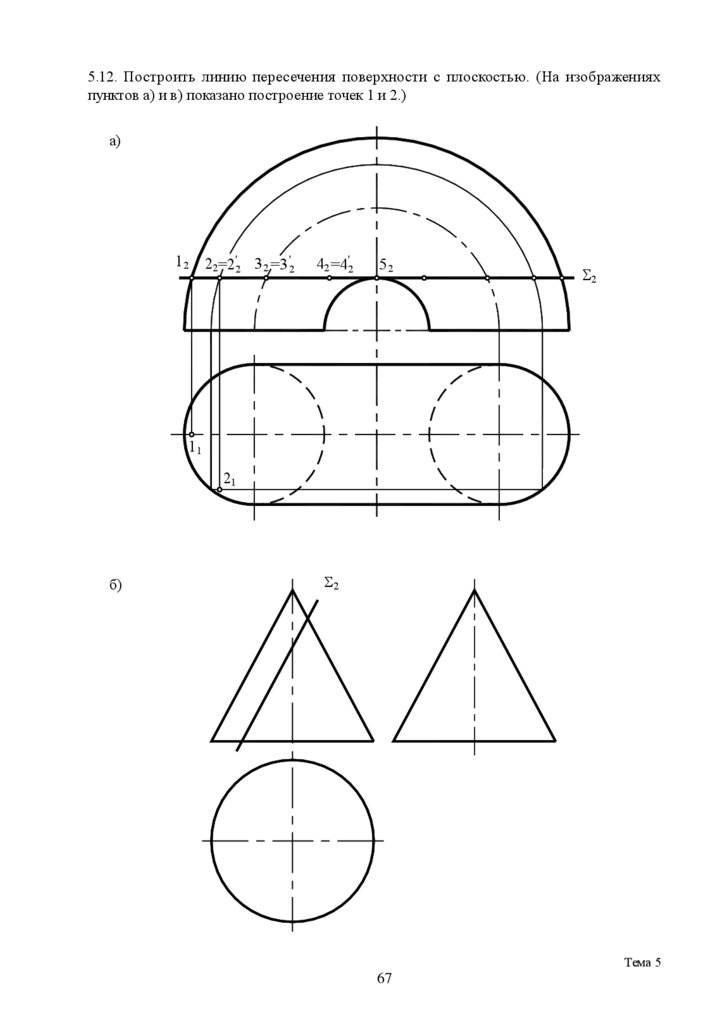
5.12. Построить линию пересечения поверхности с плоскостью. (На изображенияхпунктов а) и в) показано построение точек 1 и 2.)
а)
12
22 =2'2 3 2 =3 '2
42 =4'2
52
2
11
21
б)
2
Тема 5
67
19.
в)12
22
11
21
1
5.13. Построить три проекции фигуры с вырезом.
а)
б)
Тема 5
68
20.
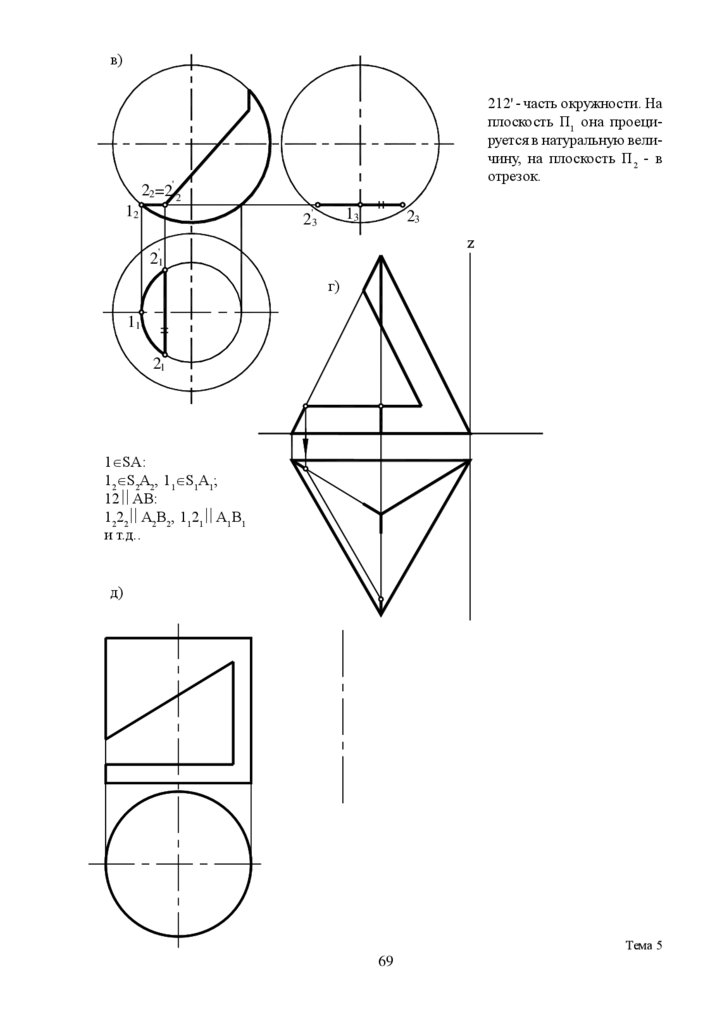
в)212' - часть окружности. На
плоскость П1 она проецируется в натуральную величину, на плоскость П 2 - в
отрезок.
22 =2' 2
12
13
2'3
23
2'1
г)
11
21
1 SA:
12 S2A2, 11 S1A1;
12 AB:
1222 A2B2, 1121 A1B1
и т.д..
д)
Тема 5
69
21.
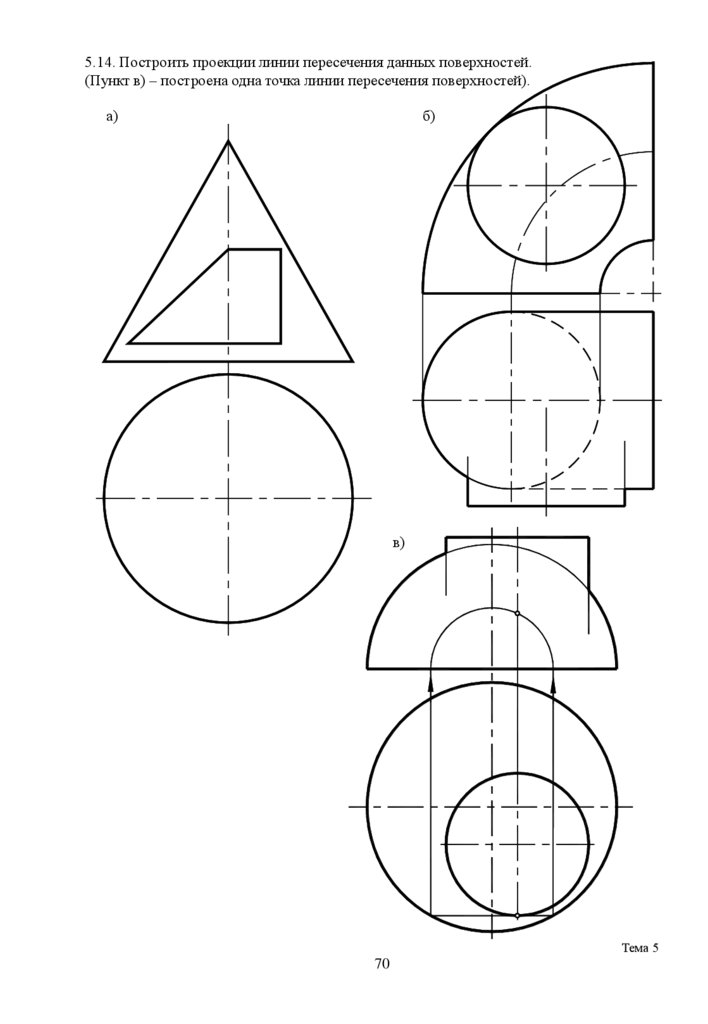
5.14. Построить проекции линии пересечения данных поверхностей.(Пункт в) – построена одна точка линии пересечения поверхностей).
а)
б)
в)
Тема 5
70






 drafting
drafting








