Similar presentations:
Уравнение прямой
1.
Уравнение прямой2. Уравнение прямой на координатной плоскости
23.
Уравнения прямыхПрямые
на координатной
плоскости могут
располагаться
только тремя
способами:
• горизонтально
• вертикально
• под наклоном к
осям
3
4.
Уравнение вертикальных прямыхУравнение вида x = a
на координатной плоскости задает
множество точек, имеющих одну и ту же
абсциссу.
Рассмотрим, например, уравнение:
x=1
Отметим на координатной плоскости
некоторые точки, имеющие абсциссу,
равную 1.
4
5.
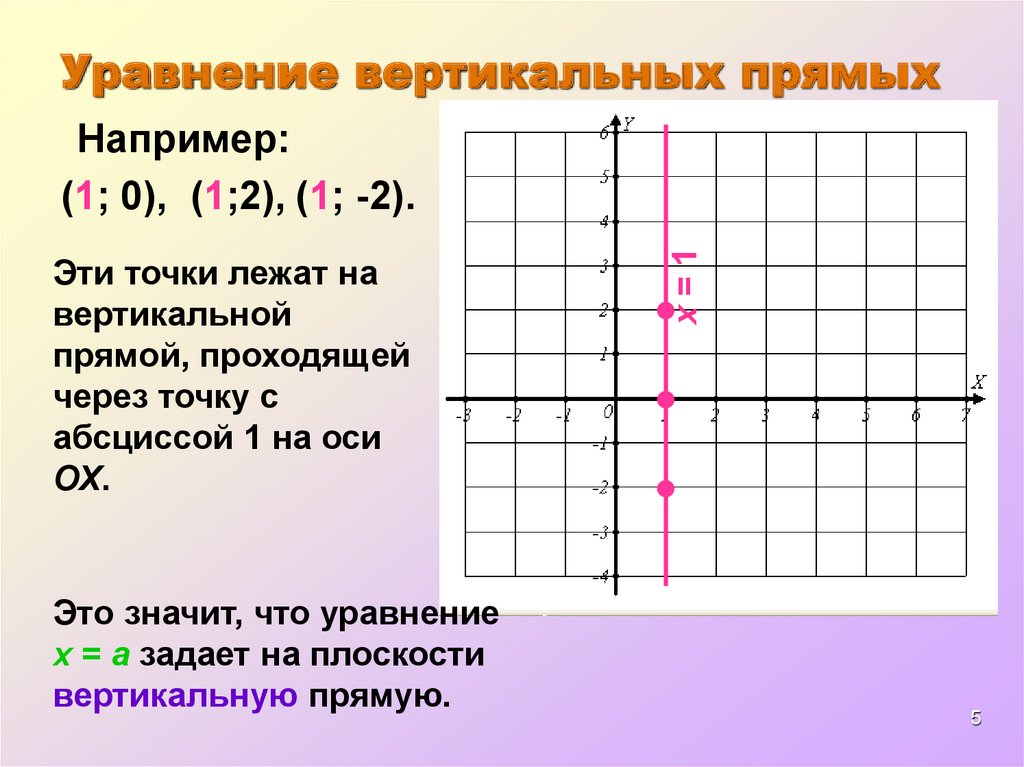
Уравнение вертикальных прямыхЭти точки лежат на
вертикальной
прямой, проходящей
через точку с
абсциссой 1 на оси
ОХ.
Это значит, что уравнение
x = a задает на плоскости
вертикальную прямую.
х=1
Например:
(1; 0), (1;2), (1; -2).
5
6.
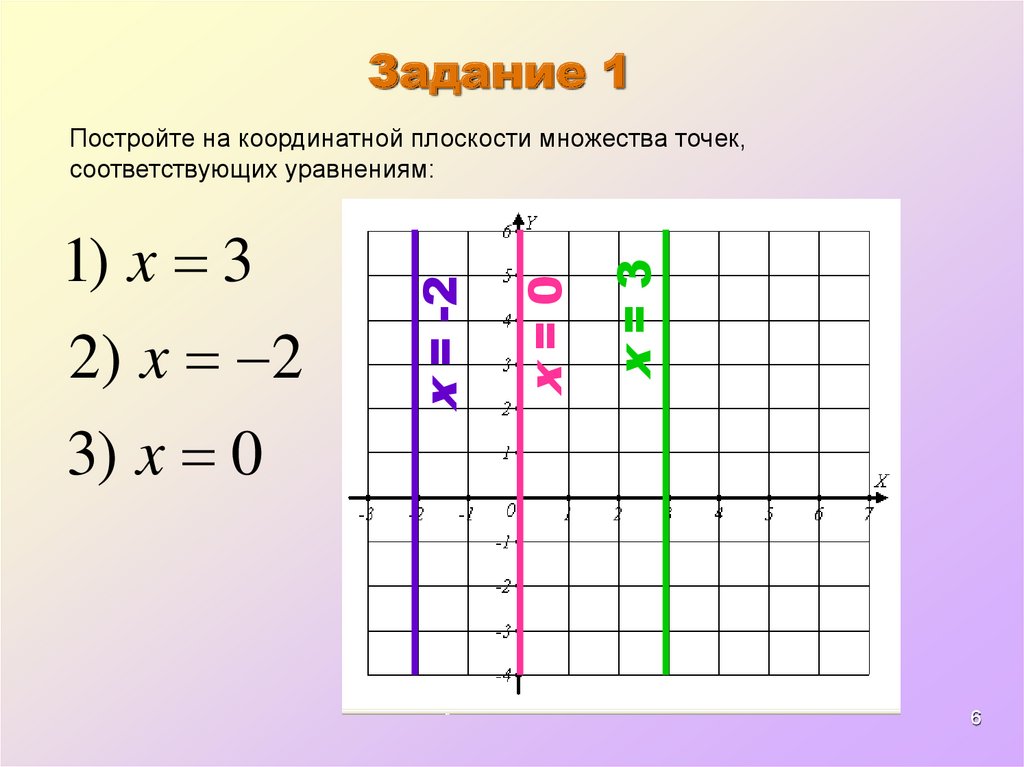
Задание 13) x 0
x=3
2 ) x 2
x=0
1) x 3
x = -2
Постройте на координатной плоскости множества точек,
соответствующих уравнениям:
6
7.
Уравнение горизонтальныхпрямых
Уравнение вида y = b
на координатной плоскости задает
множество точек, имеющих одну и ту же
ординату.
Рассмотрим, например, уравнение:
y=1
Отметим на координатной плоскости
некоторые точки, имеющие ординату,
равную 1.
7
8.
Уравнение горизонтальныхпрямых
Например:
(0; 1), (2;1), (-2; 1).
Эти точки лежат на
вертикальной
прямой, проходящей
через точку с
абсциссой 1 на оси
ОХ.
Это значит, что уравнение
y = b задает на плоскости
горизонтальную прямую.
y=1
8
9.
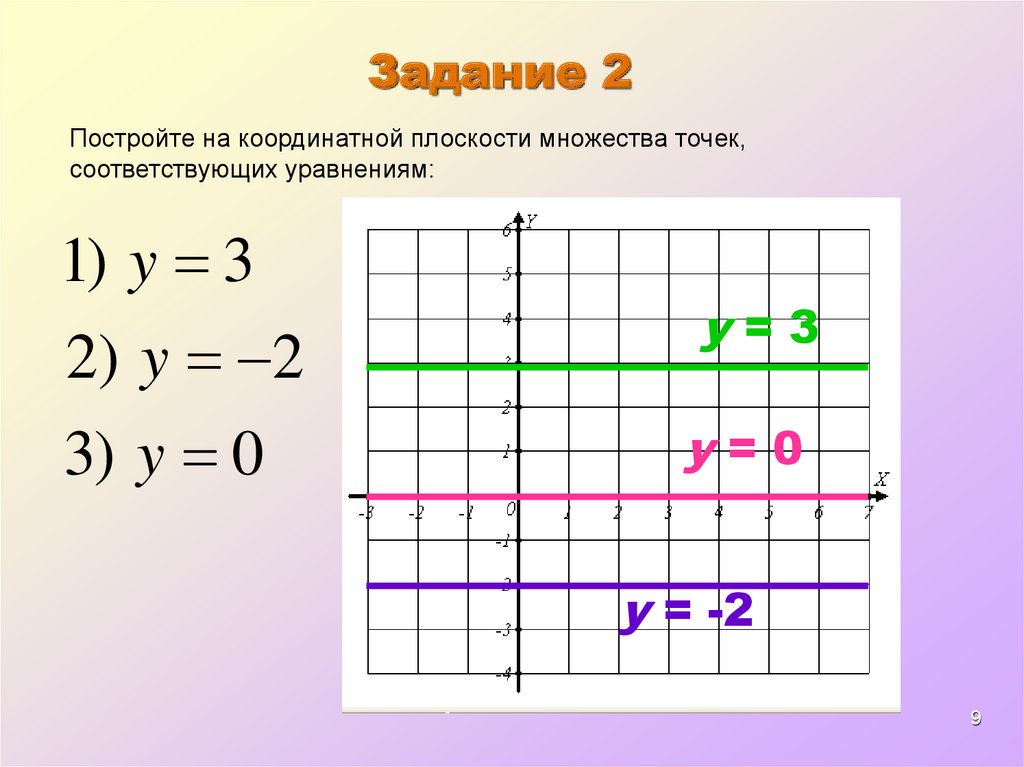
Задание 2Постройте на координатной плоскости множества точек,
соответствующих уравнениям:
1) y 3
2 ) y 2
3) y 0
y=3
y=0
y = -2
9
10.
Каноническое уравнение прямыхМы привыкли к тому, что на координатной плоскости
прямая - это график линейной функции, которая
задана уравнением вида:
y kx b
Рассмотрим следующее уравнение прямой:
Каноническая
запись
2
1
y x
3
2
6 y 4 x 3
4x 6 y 3 0
10
11.
Каноническое уравнение прямыхВ общем виде:
Ax By C 0
В канонической записи уравнения прямых принято
использовать целые коэффициенты.
Выполним обратную операцию:
By Ax C
A
C
y x
B
B
То есть:
A
k
B
C
b
B
11
12.
Задание 3Постройте на координатной плоскости множества точек,
соответствующих уравнениям:
1) y x 3
2) y 2 x 1
2
1
3) 4 x 6 y 3 0
3
12
13.
Условие параллельностипрямых
Пусть заданы уравнения прямых:
l : y k1x b1
m : y k 2 x b2
l m, если k1 k2
Например:
a: y 2 x 5
b : y 2x 7
k1 k 2 2 , то есть
a b
13
14.
Уравнение прямой, проходящейчерез две заданные точки
Запишем уравнение
прямой, проходящей
через точки А и В:
y kx b
A( xA ; yA ), B( xB ; yB ),
Если прямая проходит через точки А и В, то координаты
этих точек можно подставить в уравнение прямой:
y A kxA b
yB kxB b
Получаем систему
линейных уравнений с
неизвестными k и b.
Решив ее, находим
значения k и b.
14
15.
Уравнение прямой, проходящейчерез две заданные точки
Запишем уравнение
прямой, проходящей
через точки :
y kx b
A( 2; 1), B(2; 3),
Подставим координаты в уравнение прямой:
1 2k b k 0,5
b
2
3
2
k
b
Решаем систему
Ответ: y 0,5 x 2
линейных уравнений с
1 k ( 2) b
3 k 2 b
неизвестными k и b.
15
16.
ЗаданиеНа координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
16
17.
ЗаданиеНа координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
17
18.
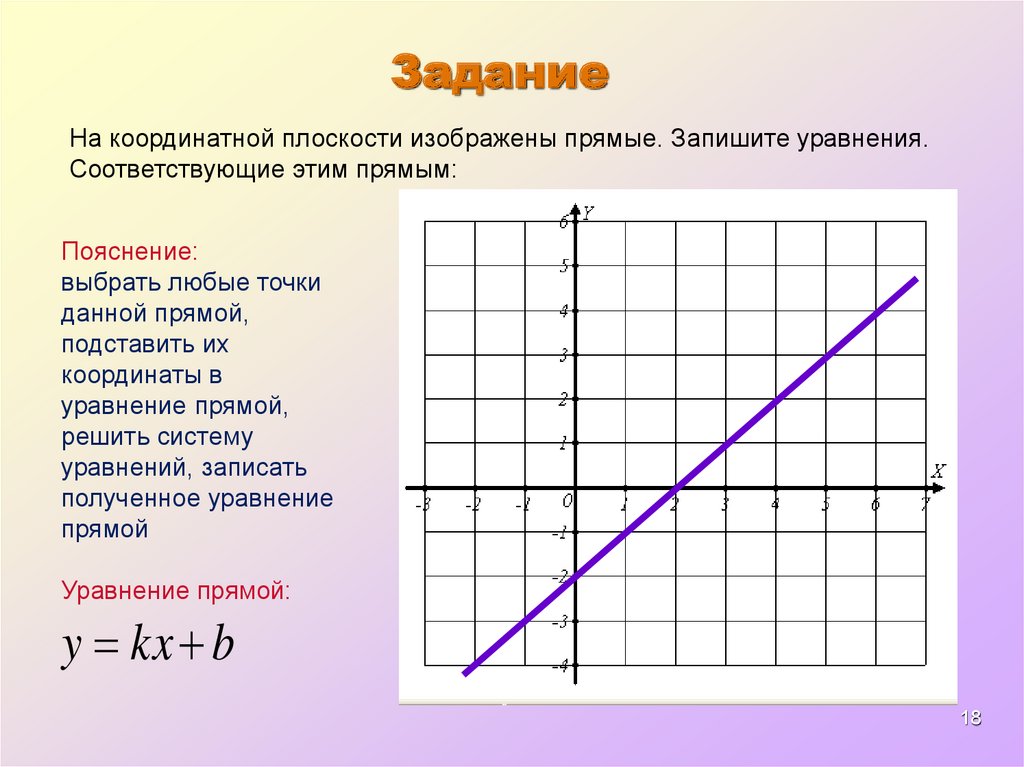
ЗаданиеНа координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
Пояснение:
выбрать любые точки
данной прямой,
подставить их
координаты в
уравнение прямой,
решить систему
уравнений, записать
полученное уравнение
прямой
Уравнение прямой:
y kx b
18
19.
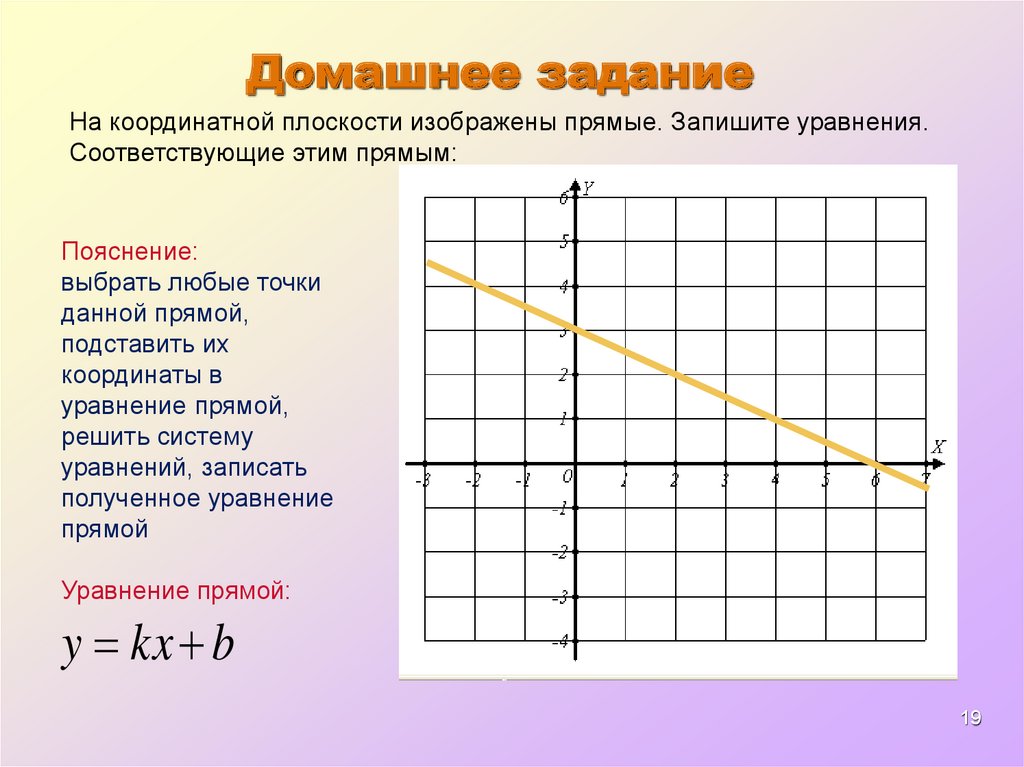
Домашнее заданиеНа координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
Пояснение:
выбрать любые точки
данной прямой,
подставить их
координаты в
уравнение прямой,
решить систему
уравнений, записать
полученное уравнение
прямой
Уравнение прямой:
y kx b
19














 mathematics
mathematics








