Динамика. Лекция 2

1.

Динамика
1) масса
2) импульс
3) сила
company name
m
Масса
масса
[m]=кг
Масса- мера инертности тела.
Инертность-свойство
тела
оказывать
сопротивление при попытках привести его
в движение или изменить величину
и
направление его скорости.

2.

Динамика
Масса
инертная
III закон Ньютона
гравитационная
закон всемирного
тяготения
company name
Гравитационная и инертная
массы равны друг другу

3.

Динамика
Инертная
масса
–
коэффициент
пропорциональности между действующей на тело
силой и ускорением тела. F ma
Способ определения инертной массы:
m1V1 m2V2
company name
F 12 F 21
m
V этал
V
mэтал
Масса – мера инертности.

4.

Динамика
Гравитационная
масса
–
источник
гравитационного поля, приводит к взаимному
притяжению тел. Определяется законом всемирного
тяготения Ньютона.
m1m2
F G
2
R
Способ определения гравитационной массы:
company name
Сравнение
сил
тяжести
эталонного и неизвестного тела
Fx
m x mэтал
Fэтал
2
E
mc
мера
энергии
m
Fэтал mэтал g
Fx m x g

5.

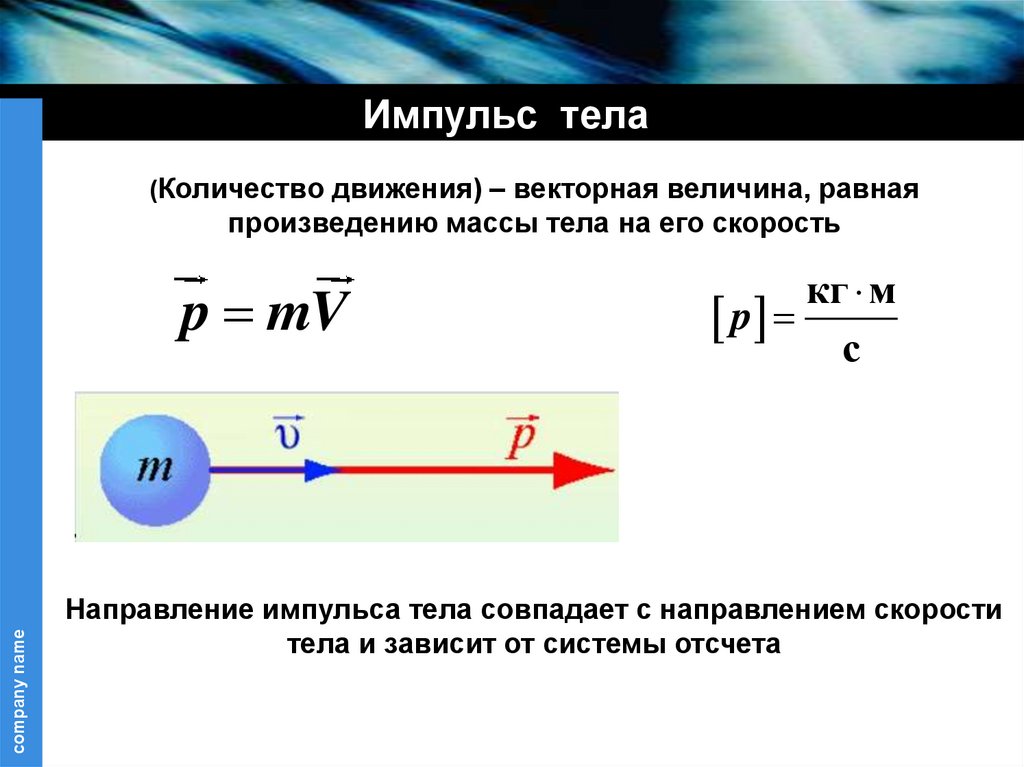
Импульс тела
(Количество движения) – векторная величина, равная
произведению массы тела на его скорость
company name
p mV
кг м
p
с
Направление импульса тела совпадает с направлением скорости
тела и зависит от системы отсчета

6.

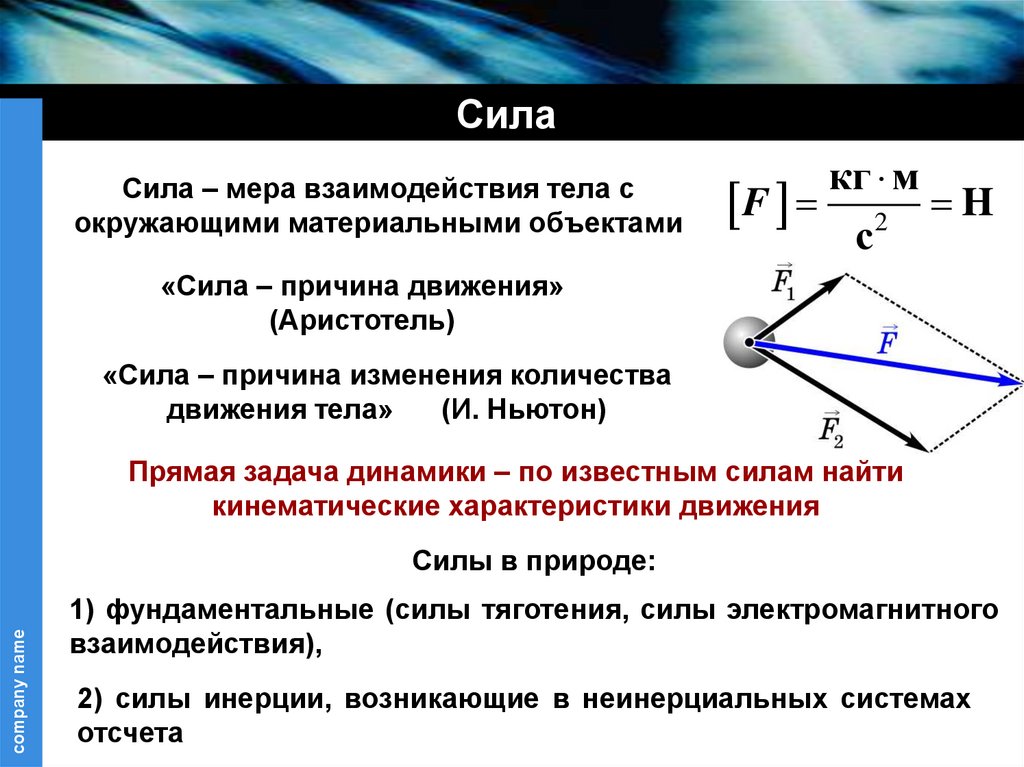
Сила
Сила – мера взаимодействия тела с
окружающими материальными объектами
кг м
F 2 H
с
«Сила – причина движения»
(Аристотель)
«Сила – причина изменения количества
движения тела»
(И. Ньютон)
Прямая задача динамики – по известным силам найти
кинематические характеристики движения
company name
Силы в природе:
1) фундаментальные (силы тяготения, силы электромагнитного
взаимодействия),
2) силы инерции, возникающие в неинерциальных системах
отсчета

7.

Сила
Силы в природе:
3) молекулярные силы (силы Ван-дер-Ваальса) – силы
взаимодействия молекул и атомов
4) силы, возникающие только при непосредственном
взаимодействии тел (силы трения, упругие силы)
5) консервативные и неконсервативные силы
company name
Если работа, совершаемая над телом, не зависит от пути, а
определяется только начальным и конечным положениями тела в
пространстве, то поле сил называется потенциальным, а сами
силы – консервативными (потенциальными).
Силы, работа которых зависит от формы пути, по
которому тело переходит из одного положения в другое,
называются неконсервативными (диссипативными).

8.

Законы Ньютона
«Математические начала натуральной философии»
(1687г.) Исаак Ньютон
Механика – классическая, квантовая, релятивистская
Основа классической механики – законы Ньютона
Первый закон Ньютона (закон инерции)
company name
Второй закон Ньютона
(основное уравнение динамики поступательного движения)
Третий закон Ньютона
(закон взаимности действия)

9.

1 закон Ньютона
Первый закон Ньютона (закон инерции): всякая материальная точка
(тело) сохраняет состояние покоя или равномерного прямолинейного
движения до тех пор, пока воздействие со стороны других тел не
заставит ее изменить это состояние.
Тело, не поддерживаемое внешними воздействиями называется
свободным.
company name
Свойство свободных тел сохранять состояние покоя или
равномерного прямолинейного движения называется инертностью
(инерцией).
Первый закон Ньютона выполняется не во всякой системе отсчета, а те
системы, по отношению к которым он выполняется, называются
инерциальными системами отсчета.

10.

1 закон Ньютона
Инерциальной системой отсчета является такая система отсчета,
относительно которой материальная точка, свободная от внешних
воздействий,
либо
покоится,
либо
движется
равномерно
и
прямолинейно.
Пример ИСО: гелиоцентрическая (звездная) система
F 0
company name
V const

11.

Принцип относительности Галилея
Все механические явления в различных
инерциальных
системах
протекают
одинаково, т.е. никакими механическими
опытами, проводимыми «внутри» данной
инерциальной
системы,
невозможно
установить,
покоится
данная
СО
или
движется прямолинейно и равномерно.
company name
Все механические процессы протекают одинаково во всех ИСО
Все системы отсчета, которые относительно инерциальной движутся
равномерно и прямолинейно, также являются инерциальными.
Систему, движущуюся ускоренно относительно инерциальной,
называют неинерциальной.
Все инерциальные системы отсчета абсолютно равноправны

12.

2 закон Ньютона
Второй закон Ньютона (основной закон динамики поступательного
движения) - ускорение, приобретаемое материальной точкой (телом),
пропорционально вызывающей силе и обратно пропорционально массе
тела.
F
a
m
company name
dp
F
dt
или
dV d mV
dp
F ma m
dt
dt
dt
dV
p mV
a
dt
- уравнение движения материальной точки
F dt d p
F dt
- импульс силы

13.

2 закон Ньютона
F dt d p
t
t
0
0
- изменение импульса материальной точки равно
импульсу силы
d p Fdt
company name
если
если
F const ,
F const ,
t
p Fdt
0
то
то
mV F
mV F t
ср t

14.

3 закон Ньютона
Третий закон Ньютона: всякое действие материальных точек (тел) друг на
друга носит характер взаимодействия; силы, с которыми действуют друг
на друга материальные точки, всегда равны по модулю, противоположно
направлены и действуют вдоль прямой, соединяющей эти точки.
company name
F 12 F 21
F12 - сила, действующая на первую материальную точку со стороны
второй;
F21 - сила, действующая на вторую материальную точку со стороны
первой.
Эти силы приложены к разным материальным точкам (телам), всегда
действуют парами и являются силами одной природы.

15.

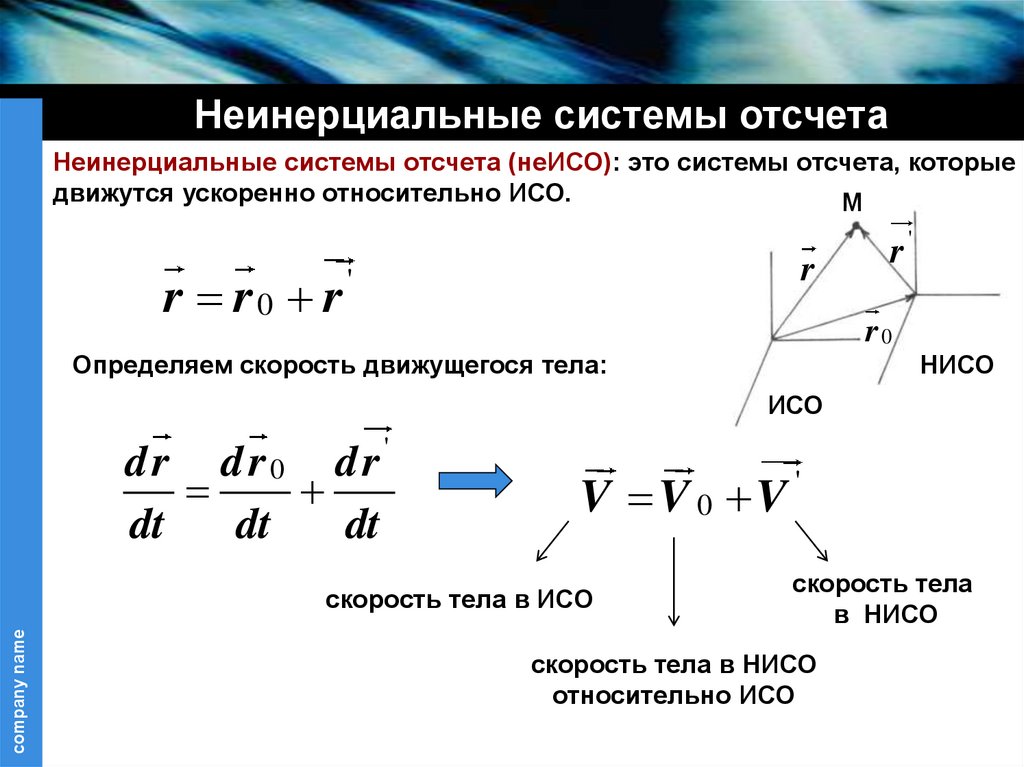
Неинерциальные системы отсчета
Неинерциальные системы отсчета (неИСО): это системы отсчета, которые
движутся ускоренно относительно ИСО.
М
r r0 r
r
'
r'
r0
Определяем скорость движущегося тела:
НИСО
ИСО
d r d r0 d r'
dt
dt
dt
V V 0 V '
company name
скорость тела в ИСО
скорость тела
в НИСО
скорость тела в НИСО
относительно ИСО

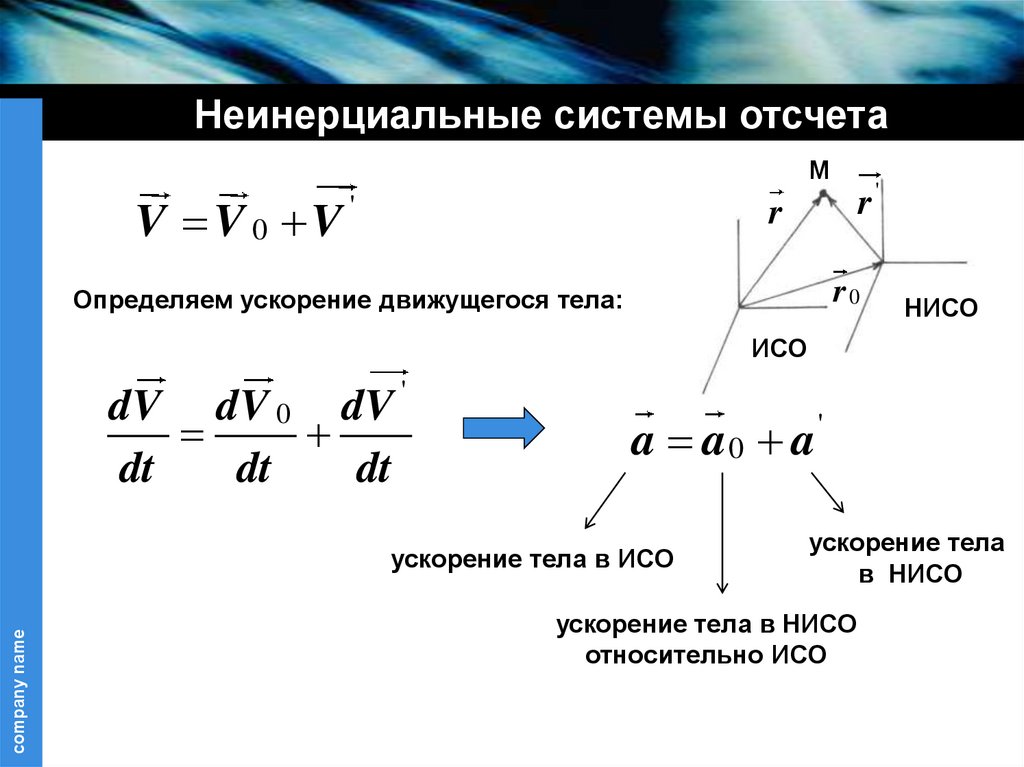
16.

Неинерциальные системы отсчета
М
V V 0 V '
r'
r
r0
Определяем ускорение движущегося тела:
НИСО
ИСО
dV dV 0 dV '
dt
dt
dt
a a0 a'
company name
ускорение тела в ИСО
ускорение тела
в НИСО
ускорение тела в НИСО
относительно ИСО

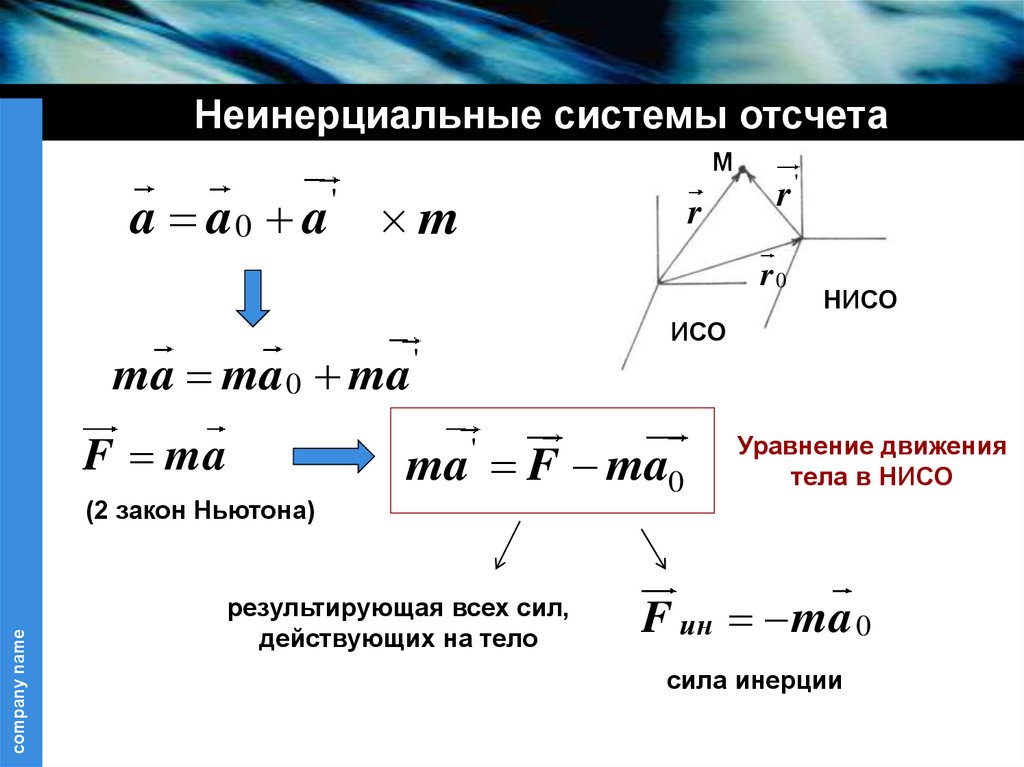
17.

Неинерциальные системы отсчета
М
a a0 a
'
m
r
r'
r0
ma ma 0 ma
F ma
company name
ИСО
'
ma F ma0
'
(2 закон Ньютона)
НИСО
результирующая всех сил,
действующих на тело
Уравнение движения
тела в НИСО
F ин ma 0
сила инерции

18.

Неинерциальные системы отсчета
ma F ma0
'
F ин ma 0
Свойства сил инерции:
1) сила инерции возникает не из-за взаимодействия тел, а лишь
вследствие ускоренного движения системы отсчета;
2) силы инерции зависят от выбора системы отсчета;
3) силы инерции не подчиняются 3 закону Ньютона;
company name
4) силы инерции пропорциональны массе тела.

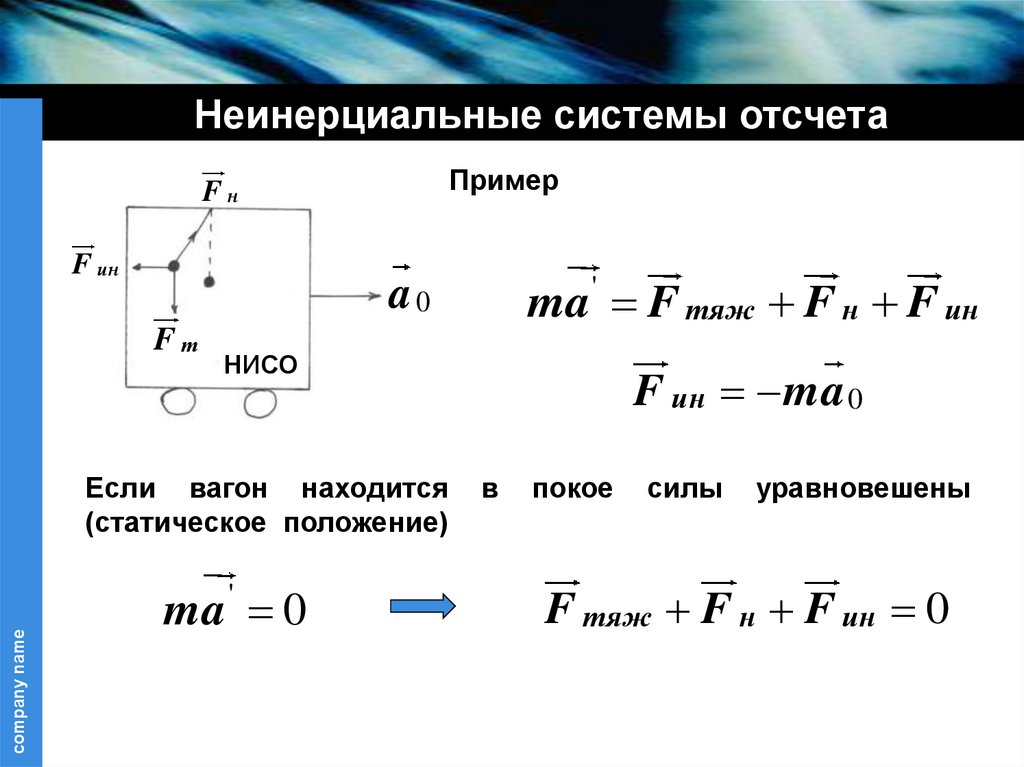
19.

Неинерциальные системы отсчета
Пример
Fн
F ин
Fт
НИСО
Если вагон находится
(статическое положение)
company name
ma ' F тяж F н F ин
a0
ma ' 0
F ин ma 0
в
покое
силы
уравновешены
F тяж F н F ин 0

20.

Закон сохранения импульса
Совокупность материальных точек (тел), рассматриваемых как единое
целое, называется механической системой.
Силы взаимодействия между материальными точками механической
системы называются внутренними.
company name
Силы, с которыми на материальные
точки системы действуют внешние
тела, называются внешними.
Механическая система тел, на которую не действуют внешние
силы, называется замкнутой (или изолированной).

21.

Закон сохранения импульса
company name
Рассмотрим механическую систему, состоящую из n тел, масса и
скорость которых равны m1, m2, ... mn ; V 1, V 2, ... V n
F 12 , F 13 , ... F ik
F 1, F 2, ... F i
- внутренние силы, действующие на 1-ое тело
со стороны 2-го, 3-го и т.д.
- внешние силы, действующие на 1-ое, 2-ое
тело и т.д.

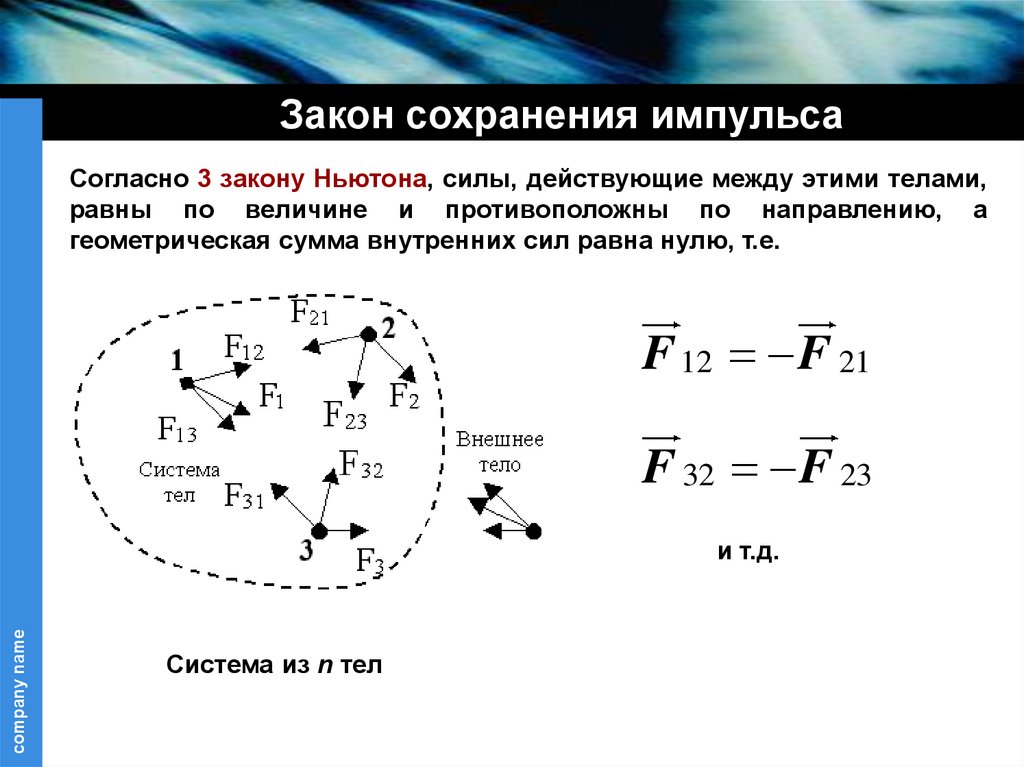
22.

Закон сохранения импульса
Согласно 3 закону Ньютона, силы, действующие между этими телами,
равны по величине и противоположны по направлению, а
геометрическая сумма внутренних сил равна нулю, т.е.
F 12 F 21
F 32 F 23
company name
и т.д.
Система из n тел

23.

Закон сохранения импульса
Запишем уравнения динамики движения
системы, согласно 2 закону Ньютона:
company name
d
d
d
m V F
12
m V F
2
F 13 ... F 1k F 1n F 1 F 1k F 1
k 2
n
2
dt
m V F
n
21
dt
i 1
F 23 ... F 2 k F 2 n F 2 F 2 k F 2
k 3
n 1
n
n
точек
n
1 1
dt
материальных
n1
F n 2 ... F nk F n,n 1 F n F nk F n
d mi Vi
dt
k 1
n
n
n
F ik F i
i 1 k 1
i 1

24.

Закон сохранения импульса
n
i 1
d mi Vi
dt
mi Vi p i
company name
импульс одной
материальной точки
n
n
n
F ik F i
i 1 k 1
n
mi Vi p
i 1
сумма
импульса
системы мат. точек
называется
импульсом системы
материальных точек
i 1
n
n
F ik 0
i 1 k 1
по 3 закону Ньютона

25.

Закон сохранения импульса
n
i 1
d mi Vi
dt
d
n
d n
dp n
mi Vi pi
F i
dt i 1
dt i 1
dt i 1
company name
dp n
Fi
dt i 1
Скорость изменения импульса системы материальных точек
равна сумме внешних сил, действующих на точки системы.

26.

Закон сохранения импульса
dp n
Fi
dt i 1
Скорость
изменения
импульса
системы
материальных точек равна сумме внешних
сил, действующих на точки системы.
В случае отсутствия внешних сил:
n
company name
p mi Vi const
i 1
Fi 0
Импульс замкнутой системы сохраняется,
т.е. не изменяется с течением времени.

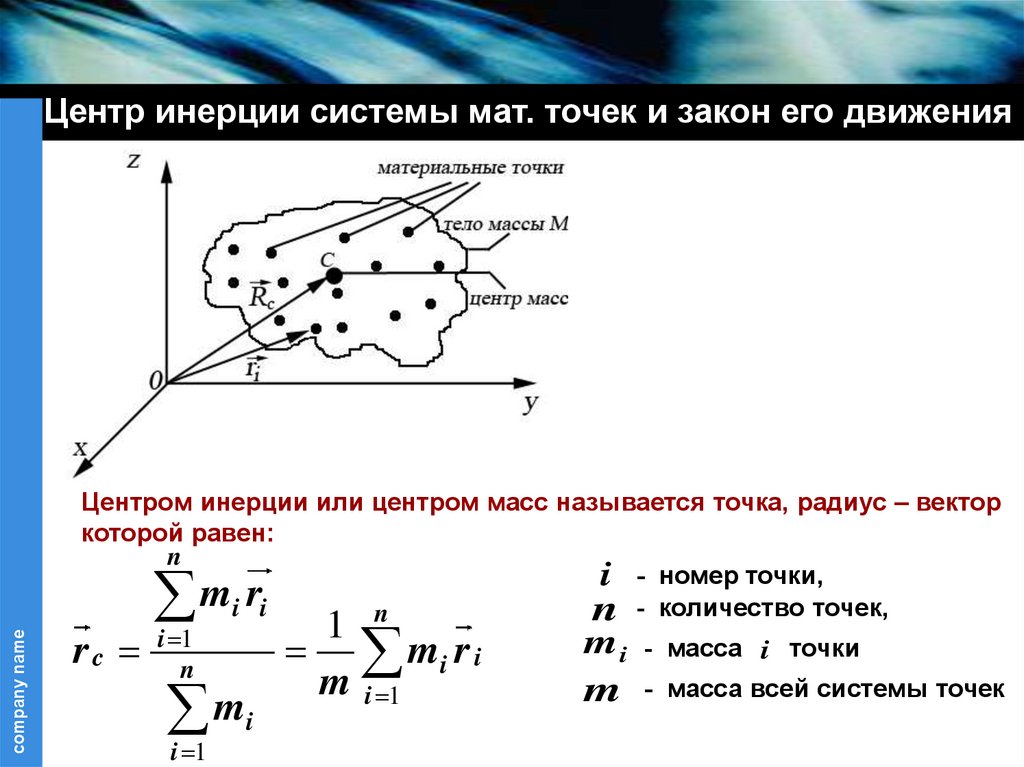
27.

Центр инерции системы мат. точек и закон его движения
Центром инерции или центром масс называется точка, радиус – вектор
которой равен:
n
i - номер точки,
mi ri
n - количество точек,
n
1
m i - масса i точки
r c i 1n
mi r i
m i 1
m - масса всей системы точек
mi
i 1
company name

28.

Центр инерции системы мат. точек и закон его движения
n
rc
mi ri
i 1
n
mi
1 n
mi r i
m i 1
i 1
1 n
xc m i x i
m i 1
n
1
yc mi yi
m i 1
1 n
zc m i z i
m i 1
company name
n
m mi
i 1
- масса всей системы точек

29.

Центр инерции системы мат. точек и закон его движения
Скорость центра инерции системы
материальных точек
d rc
Vc
dt
d rc 1 n mi d ri 1 n
Vc
mi Vi
dt m i 1 dt
m i 1
n
company name
p mi Vi mVc
i 1
Импульс системы материальных точек
равен произведению масс всей системы
на скорость ее центра инерции

30.

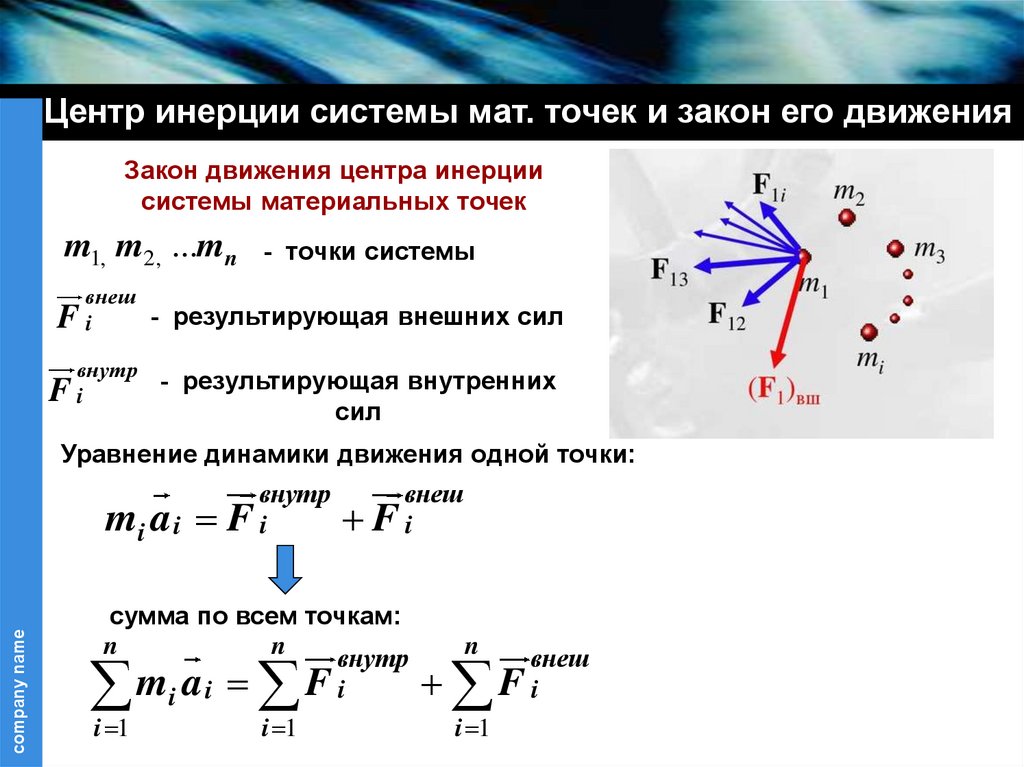
Центр инерции системы мат. точек и закон его движения
Закон движения центра инерции
системы материальных точек
m1, m2, ...mn
- точки системы
внеш
- результирующая внешних сил
Fi
внутр
- результирующая внутренних
Fi
сил
Уравнение динамики движения одной точки:
company name
mi a i
внутр
Fi
внеш
Fi
сумма по всем точкам:
n
n
внутр
mi a i F i
i 1
i 1
n
i 1
внеш
Fi

31.

Центр инерции системы мат. точек и закон его движения
n
n
mi a i ?
i 1
n
внутр
Fi
n
?
i 1
?
i 1
2
n
внеш
Fi
n
2
d ri
d
mi a i mi dt 2 dt 2 mi r i
i 1
i 1
i 1
n
n
d2 n
d2
d 2 rc
2 mi r i 2 r c mi mi
ma c
2
dt i 1
dt
dt
i 1
i 1
company name
n
mi a i ma c
i 1
масса системы
ускорение центра масс

32.

Центр инерции системы мат. точек и закон его движения
n
Если
внутр
Fi
0,
т.к.
F ik F ki
i 1
n
i 1
внеш
Fi
n
0
ma c F
внеш
i 1
company name
Закон движения центра масс
системы материальных точек
Центр масс системы материальных точек движется как
материальная точка, масса которой равна массе всей системы, и на
которую действует сила, равная результирующей всех внешних сил,
приложенных к системе.

33.

Центр инерции системы мат. точек и закон его движения
Основное
уравнение
динамики
поступательного движения твердого тела
n
ma c F
внеш
i 1
Твердое тело можно рассматривать как
систему
материальных
точек,
поэтому
полученное уравнение называют основным
уравнением
динамики
поступательного
движения твердого тела.
Следствия:
1)
n
company name
i 1
внеш
Fi
0
dV
ma c m
0
dt
n
mV c mi V i const
i 1
закон сохранения импульса

34.

Центр инерции системы мат. точек и закон его движения
Следствия:
d mV
2)
n
i 1
внеш
Fi
0
dt
n
F
внеш
i 1
n
d p F
внеш
dt
i 1
company name
Изменение
импульса
системы
материальных точек равно импульсу
внешних сил