Similar presentations:
Полярные координаты. Параметрическая форма кривых
1. Линейная алгебра и аналитическая геометрия
Тема: Полярные координаты.Параметрическая форма кривых.
Лектор Имас О.Н.
2018 г.
2.
Кривой 2-го порядка на плоскости называют геометрическое место точекM(x;y), удовлетворяющих уравнению F(x;y)=0.
Или
i j
a
x
ij y 0, max(i j ) 2
i , j n
Q( x1; x2 ;...; xn )
a xx
i , j n
Рассмотрим Q(x1;x2)
ij i
j
Функция Q называется квадратичной формой
a xx
i , j n
ij i
j
a11x12 a12 x1x2 a21x2 x1 a22 x2 2
a11 a12
Матрица A
называется матрицей квадратичной формы, где aij a ji
a21 a22
1 0
Диагональная матрица вида
, полученная из матрицы А путем
0
2
преобразования координат, называется канонической формой матрицы А
3.
Вопрос. Как найти эти новые координаты, т.е этот новый базис?Очевидно, должно выполняться: АХ= X AX- X=0 (A- E)X=0
(A- E)X=0 – система линейных однородных уравнений, из которой и
найдем фундаментальную систему решений Х, они-то и будут новым
базисом, в котором квадратичная форма примет каноническую форму
Определение. Матрица A- E называется характеристической матрицей
| A- E | называется характеристическим
Определение. Определитель
многочленом от .
a11
a12
a21
a22
Определение. Корни характеристического многочлена | A- E | 0 называются
собственными числами, а ненулевые решения системы (A- E)X=0
называются собственными векторами.
пропустить 3 страницы
4. Поверхности второго порядка
Поверхностью второго порядка называется геометрическоеместо точек в пространстве, декартовы координаты которых
удовлетворяют уравнению F(x,y,z) = 0,
F(x,y,z) – многочлен степени 2.
В общем случае :
a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a10x+2a20y+2a30z+a00=0 .
Поверхности второго порядка делятся на
1) вырожденные
и
2) невырожденные
Вырожденные - это плоскости, точки и вырожденные (мнимые)
поверхности (уравнению не удовлетворяет ни одна точка
пространства).
Невырожденными
поверхности
второго
порядка
подразделяются на пять типов.
Эллипсоид,
Гиперболоид (однополосный и двуполостный),
Конус,
Параболоид
Цилиндрическая поверхность
5.
Названиеповерхности
Сфера
Аналитический вид
( x x0 )2 ( y y0 )2 ( z z0 )2 r 2
M0(x0;y0;z0) – центр сферы, r – радиус
Эллипсоид
Цилиндр
Конус
( x x0 )2 ( y y0 )2 ( z z0 )2
1
a2
b2
c2
M0(x0;y0;z0) – центр эллипсоида, a, b, с – полуоси
( x x0 ) 2 ( z z0 ) 2
1 Ось l | | Oy
а)
a2 2
b2 2
( x x0 )
( y y0 )
1
2
б)
Ось l | | Oz
a
b2
( x x0 )2 ( y y0 )2 ( z z0 )2
M0(x0;y0) – вершина конуса
Эллиптический
параболоид
( x x0 )2 ( y y0 )2 2 p( z z0 )
Гиперболоид
(однополостный)
( x x0 )2 ( y y0 )2 ( z z0 ) 2
1
2
2
2
a
b
c
Гиперболоид
(двуполостный)
( x x0 )2 ( y y0 )2 ( z z0 ) 2
1
2
2
2
a
b
c
Графическое изображение
6.
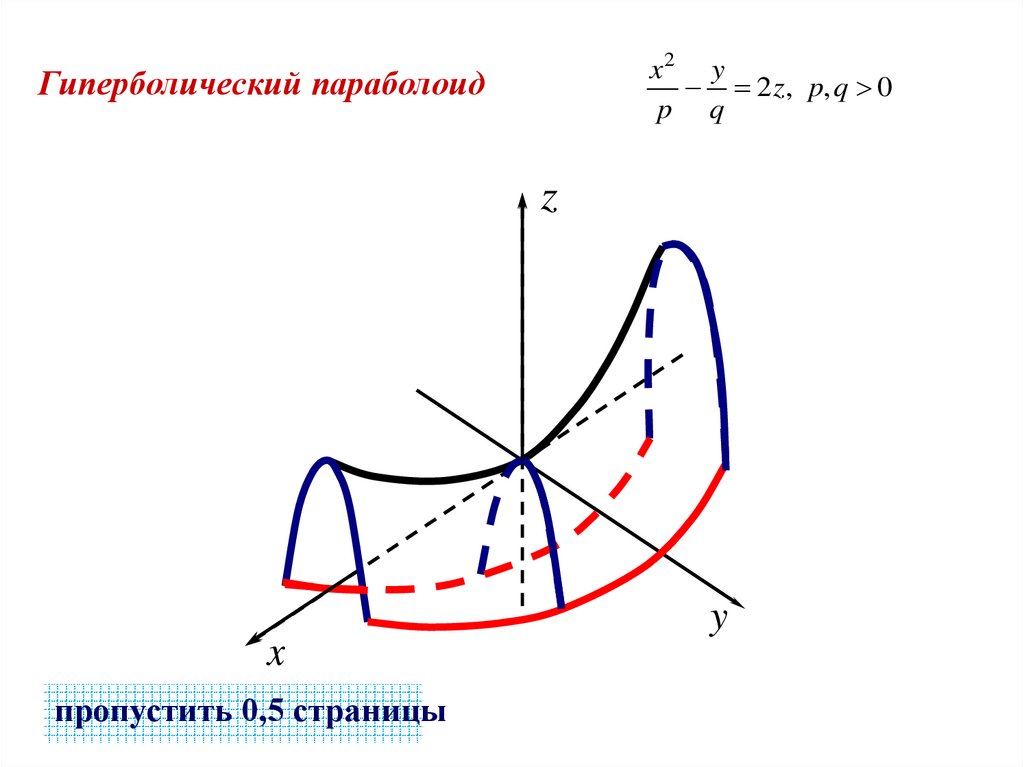
x2 y2 z, p, q 0
p q
Гиперболический параболоид
z
x
пропустить 0,5 страницы
y
7.
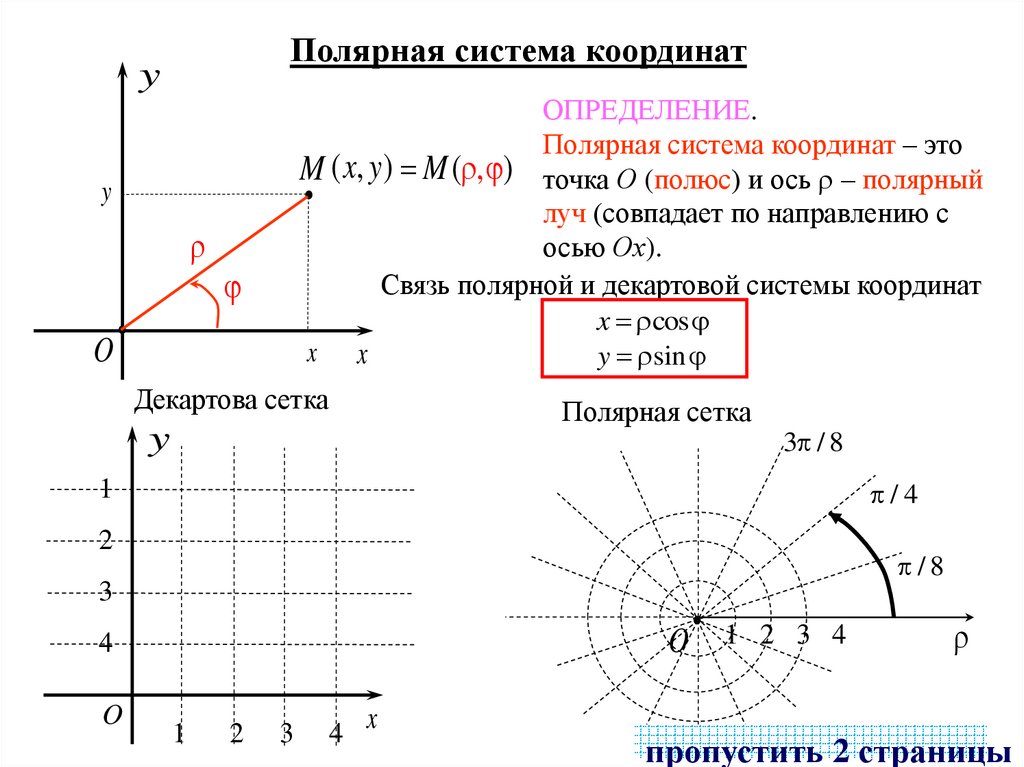
Полярная система координатy
ОПРЕДЕЛЕНИЕ.
Полярная система координат – это
M ( x, y) M ( , ) точка О (полюс) и ось – полярный
луч (совпадает по направлению с
осью Ох).
Связь полярной и декартовой системы координат
x cos
x x
y sin
y
O
Декартова сетка
Полярная сетка
y
3 / 8
/4
1
2
/8
3
O
4
O
1
2
3
4 x
1 2 3 4
пропустить 2 страницы
8. 5. Построение графиков функций, заданных параметрически
Пример.Построить кривую, заданную уравнением x a cos t ,
y b sin t
Подготовим таблицу значений x и y
t
x
y
0
a
0
/6
√3/2 a
½b
/4
√2/2 a
√2/2 b
/3
½a
√3/2 b
/2
0
b
пропустить 1 страницу
в I четверти
y
O
x






 mathematics
mathematics








