Свойства параллельных плоскостей

1.

Геометрия 10 класс
Тема:
«Свойства параллельных
плоскостей»

2.

Геометрия в своей сути и есть пространственное
воображение, пронизанное и организованное строгой
логикой.
В ней всегда присутствуют эти два неразрывно
связанных элемента: наглядная картина и точная
формулировка, строгий логический вывод.
Там, где нет одной из этих сторон, нет и подлинной
геометрии.
А. Д. Александров

3.

Тема урока:
«Свойства параллельных плоскостей»
Цели урока:
• познакомиться со свойствами
параллельных плоскостей;
• доказать свойства параллельных
плоскостей;
• научиться применять свойства
параллельных плоскостей при
решении задач.

4.

1. Верно ли, что если две пересекающиеся прямые,
лежащие в одной плоскости, параллельны другой плоскости,
то эти плоскости параллельны. Верно
2. Верно ли, что если две прямые, лежащие в одной
плоскости, параллельны двум прямым другой плоскости,
то эти плоскости параллельны. Нет
Привести контрпример – пересекающиеся плоскости,
проведенные через параллельные прямые.

5.

D
Е
A
3. Дано: ∟DAB + ∟ AEP = 180°,
∟ DBC + ∟ ТРВ = 180°.
Доказать, что (АВС) || (ЕРТ)
Т
Р
C
B
4. Каким может быть взаимное расположение прямой а и
плоскости β, если прямая а лежит в плоскости α,
параллельной плоскости β?

6.

5. Как могут быть расположены плоскости α и β, если
плоскость α проходит через некоторую прямую а,
параллельную плоскости β?
6. Как могут быть расположены плоскости α и β, если
любая прямая, лежащая в плоскости α, параллельна
плоскости β?
7. Сформулируйте определение параллельных плоскостей.
8. Сформулируйте признак параллельности двух
плоскостей.
9. Каково взаимное
пространстве?
расположение
плоскостей
в

7.

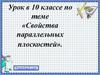
α и β совпадают
α β
α β

8.

1. Если плоскости не пересекаются, то они параллельны.
ДА
2. Плоскости параллельны, если прямая лежащая в
НЕТ
одной плоскости, параллельна другой плоскости?
3. Если две прямые, лежащие в одной плоскости,
НЕТ
параллельны двум прямым другой плоскости, то эти
плоскости параллельны?
4. Если прямая перпендикулярна одной из двух параллельных
ДА
плоскостей, то она перпендикулярна и другой плоскости.
5. Прямые, по которым две параллельные плоскости
ДА
пересечены третьей плоскостью, параллельны.
6. Если прямая пересекает одну из двух плоскостей, то
НЕТ
она пересекает и другую.
7. Две плоскости, параллельные третьей, параллельны.
ДА
8. Отрезки прямых, заключенные между
НЕТ
параллельными плоскостями, равны.

9.

а
b
Если две параллельные плоскости
пересечены третьей, то линии их
пересечения параллельны.
Дано:
α β, α = a
β =b
Доказать: a b
Доказательство:
1. a , b
2. Пусть a b,
тогда a b = М
3. M α, M β α β = с (А2)
Получили противоречие с условием.
Значит a b ч.т.д.

10.

А
В
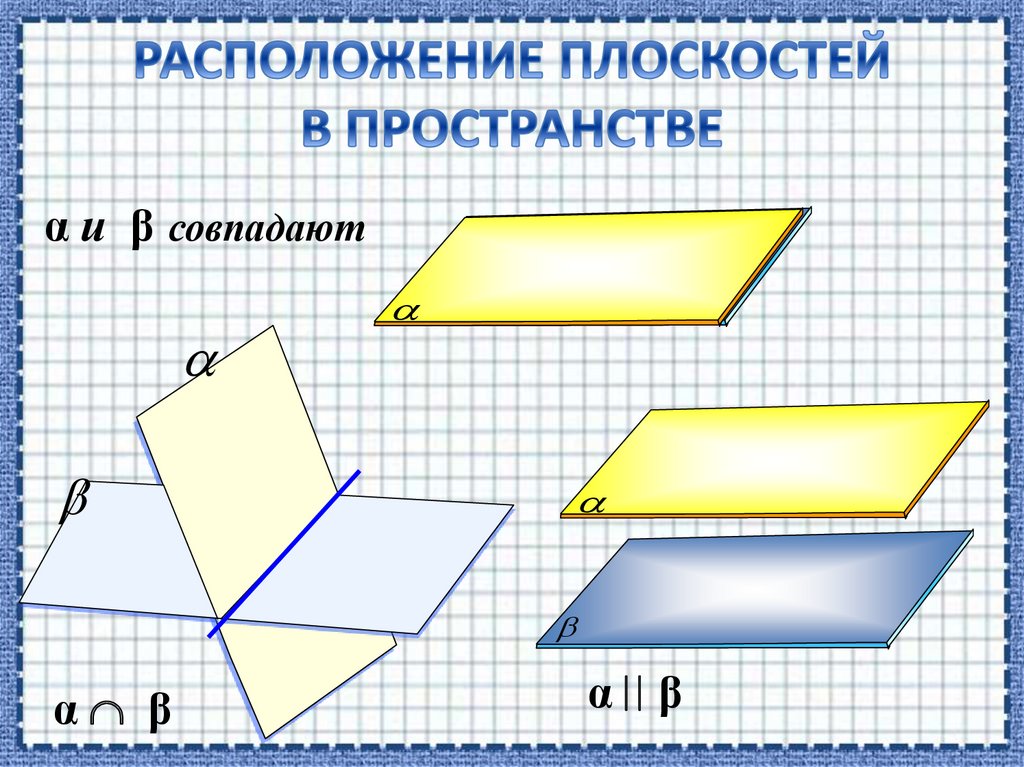
Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.
С
Дано:
α β, АВ СD
АВ α = А, АВ β = В,
СD α = С, СD β = D
Доказать: АВ = СD
Доказательство:
1. Через АВ СD проведем
D
2. α β, α = a, β = b
3. АС В D,
4. АВ СD (как отрезки парал. прямых)
5. АВСД – параллелограмм (по опр.)
АВ = СD ( по свойству параллелограмма)

11.

12.

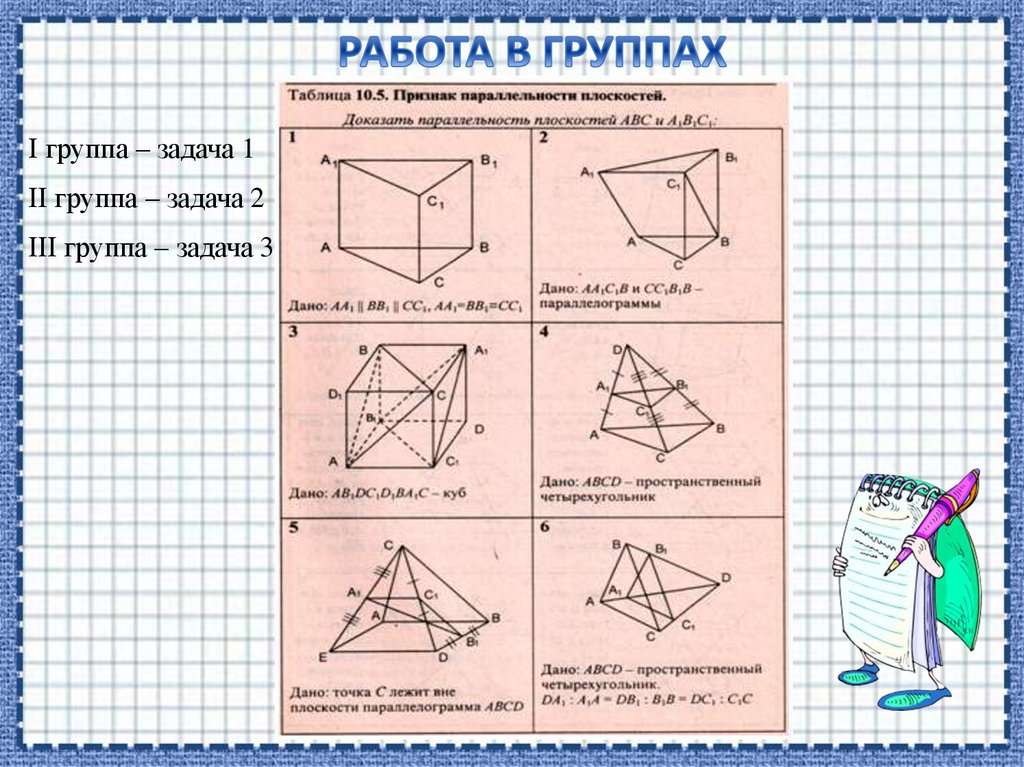
I группа – задача 1
II группа – задача 2
III группа – задача 3

13.

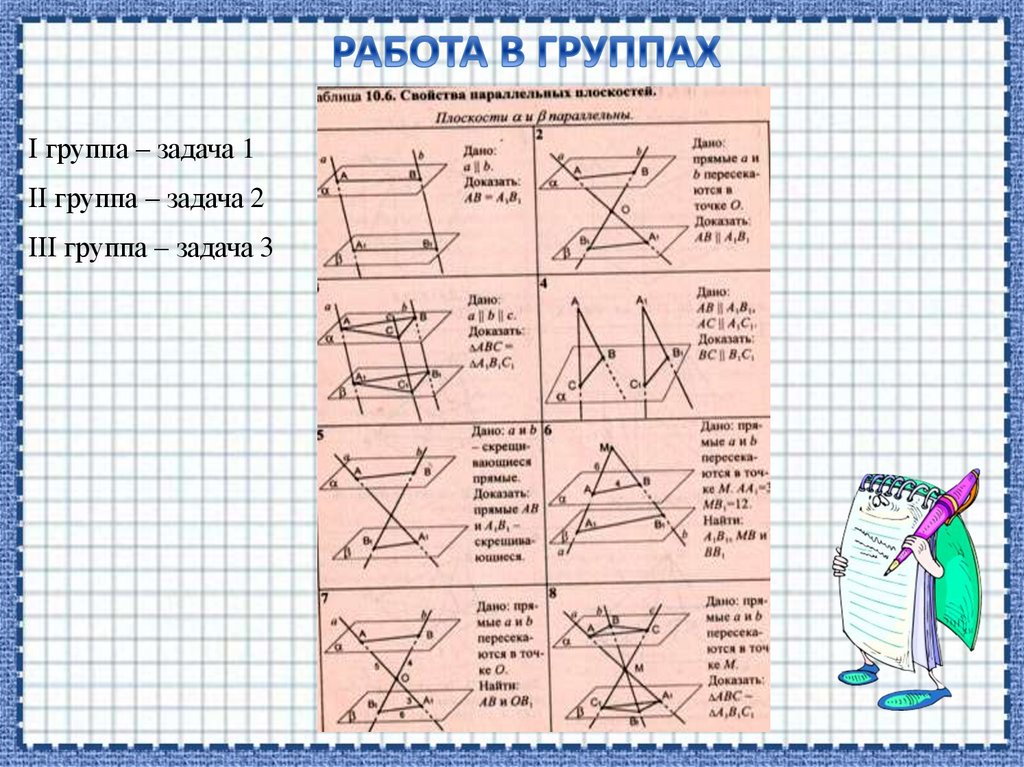
I группа – задача 1
II группа – задача 2
III группа – задача 3