Similar presentations:
Чётные и нечётные функции. Периодические функции
1.
Чётные и нечётные функции.Периодические функции.
Фомина Л.В.
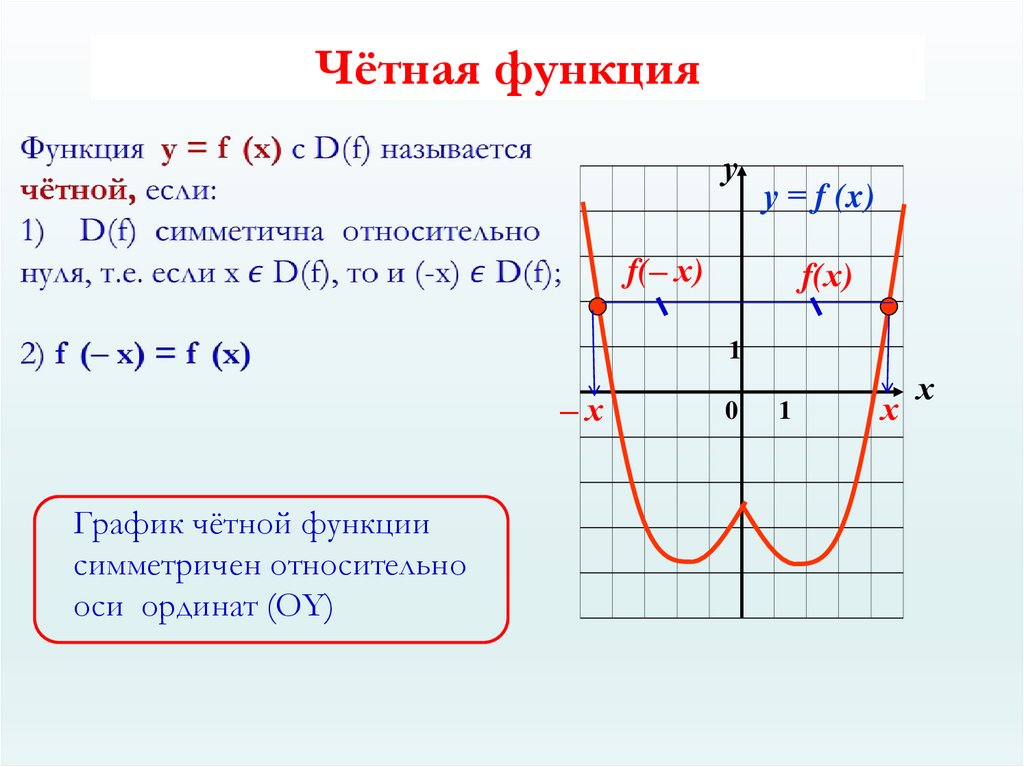
2. Чётная функция
уу = f (x)
f(‒ х)
f(х)
1
‒х
График чётной функции
симметричен относительно
оси ординат (ОY)
0
1
х
х
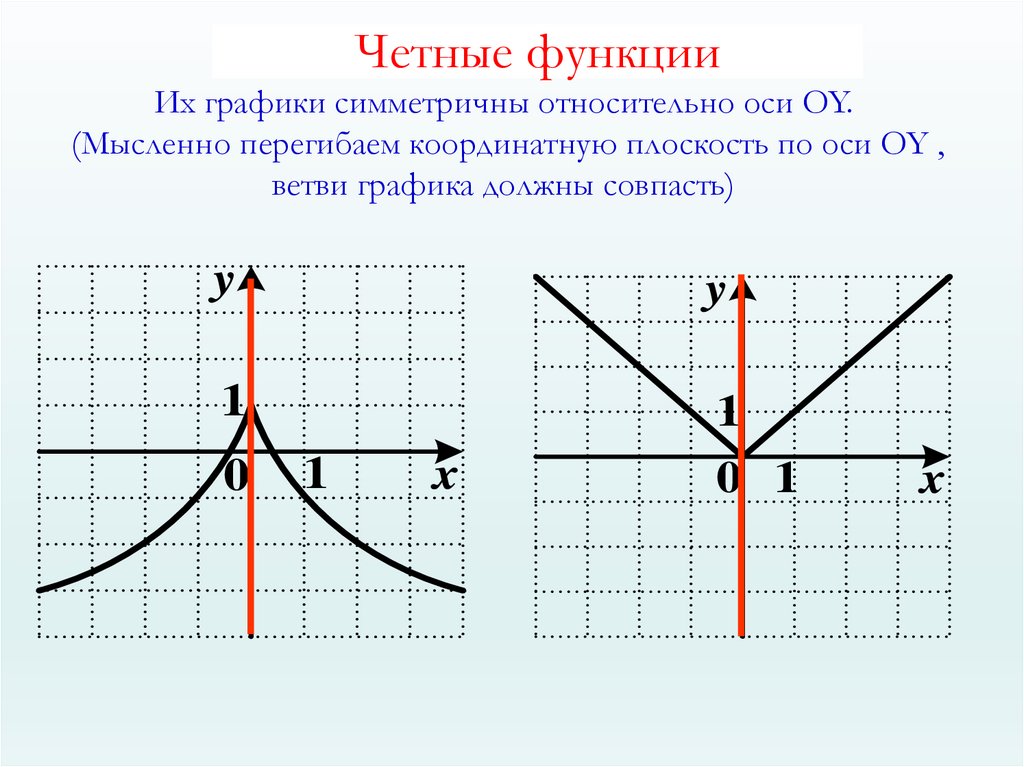
3. Четные функции
Их графики симметричны относительно оси OY.(Мысленно перегибаем координатную плоскость по оси OY ,
ветви графика должны совпасть)
y
y
1
1
0 1
0
1
x
x
4.
Примеры чётных функций1 2
у ( х) х
2
1
1 2
2
у ( х) ( х) х
2
2
у ( х) у ( х)
График данной функции
симметричен относительно
оси ОY
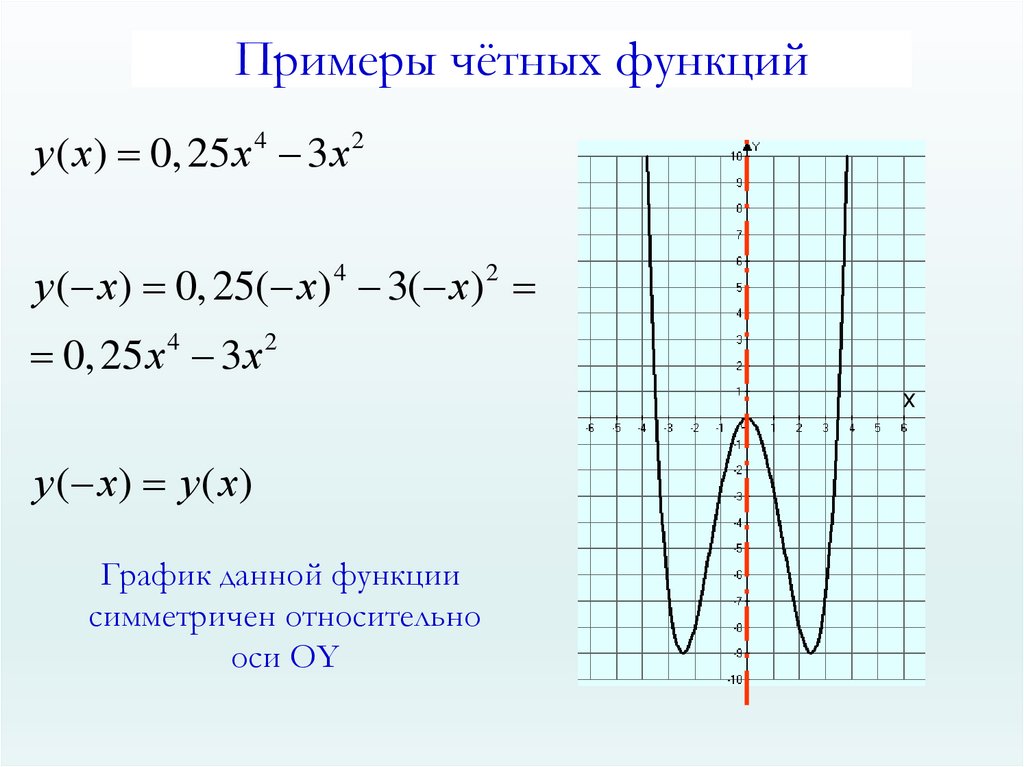
5.
Примеры чётных функцийу ( х) 0, 25 х 4 3 х 2
у ( х) 0, 25( х) 4 3( х) 2
0, 25 х 4 3 х 2
х
у ( х) у ( х)
График данной функции
симметричен относительно
оси ОY
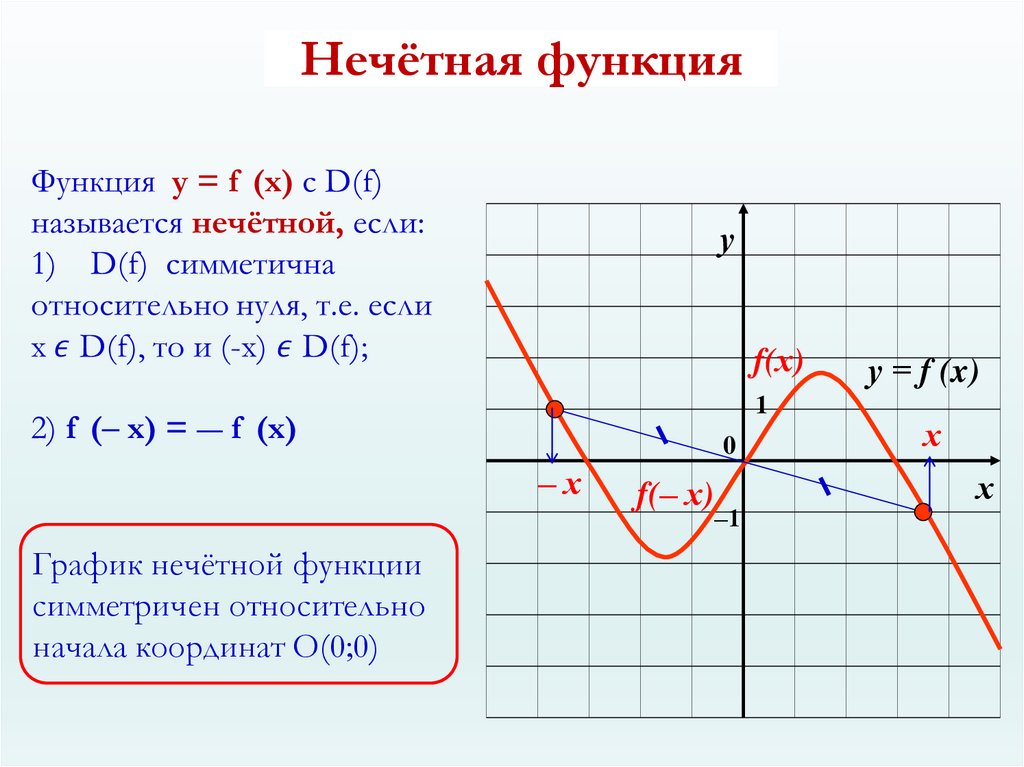
6. Нечётная функция
уf(х)
1
0
‒х
График нечётной функции
симметричен относительно
начала координат О(0;0)
f(‒ х)
‒1
у = f (x)
х
х
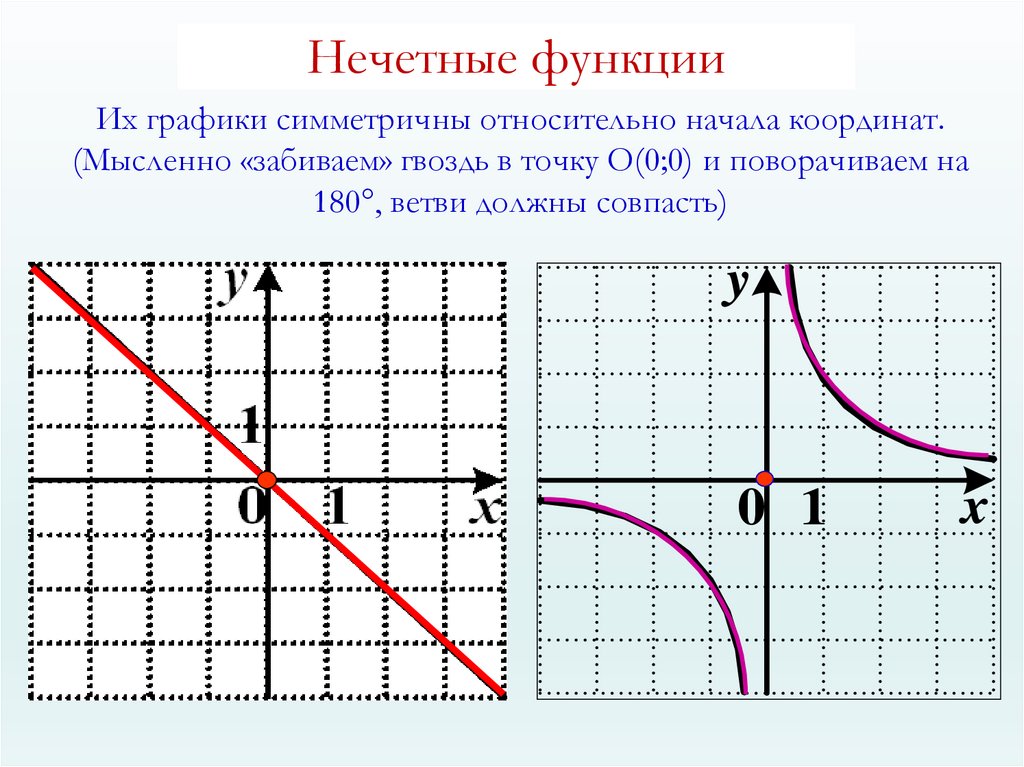
7. Нечетные функции
Их графики симметричны относительно начала координат.(Мысленно «забиваем» гвоздь в точку O(0;0) и поворачиваем на
180°, ветви должны совпасть)
y
0 1
x
8.
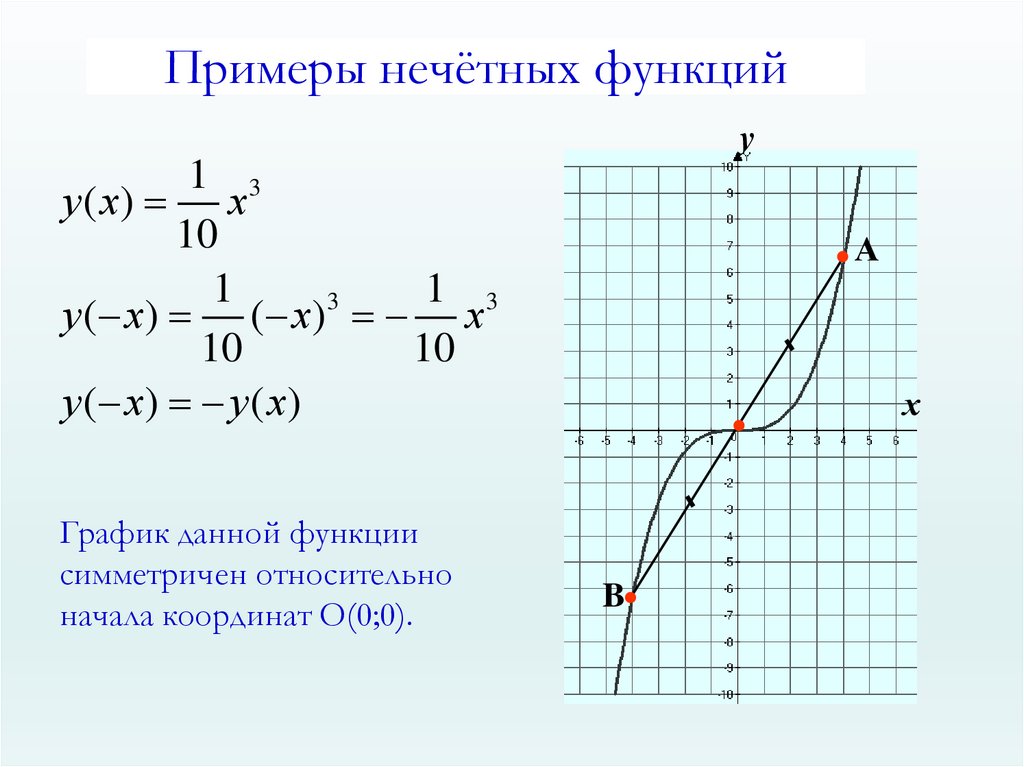
Примеры нечётных функцийу
1 3
у ( х) х
10
1
1 3
3
у ( х) ( х) х
10
10
у ( х) у ( х)
График данной функции
симметричен относительно
начала координат О(0;0).
А
х
B
9.
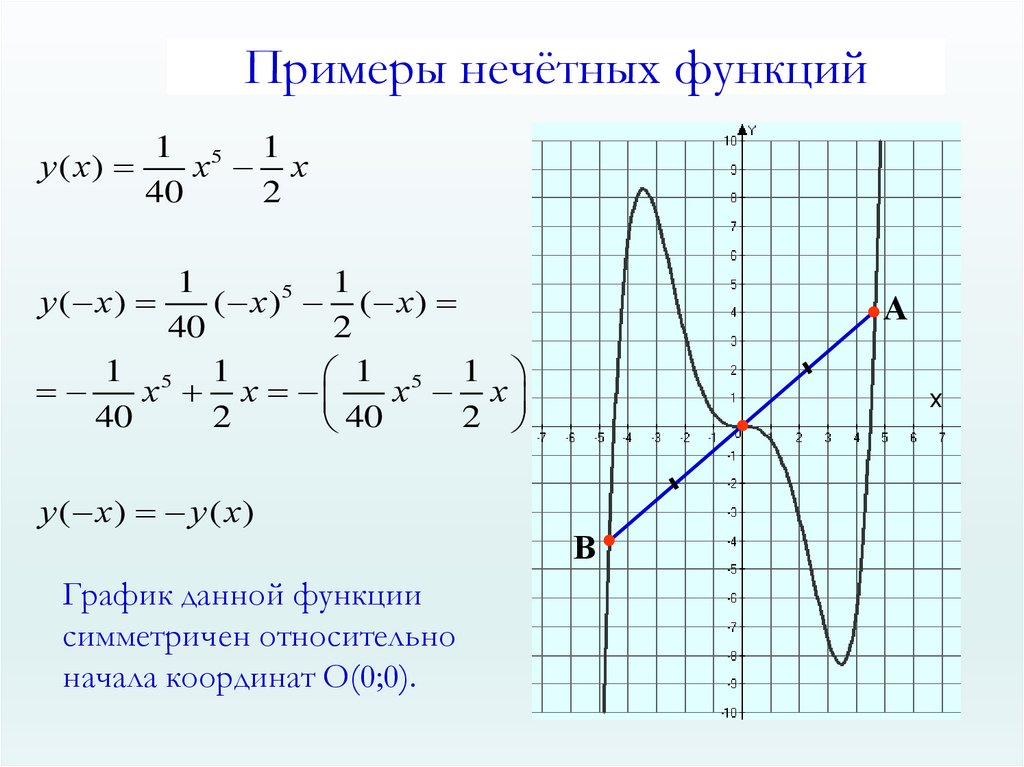
Примеры нечётных функций1 5 1
у ( х)
х х
40
2
1
1
5
у ( х)
( х ) ( х)
40
2
1 5 1
1 5 1
х х
х
40
2
2
40
у ( х) у ( х)
График данной функции
симметричен относительно
начала координат О(0;0).
А
х
х
В
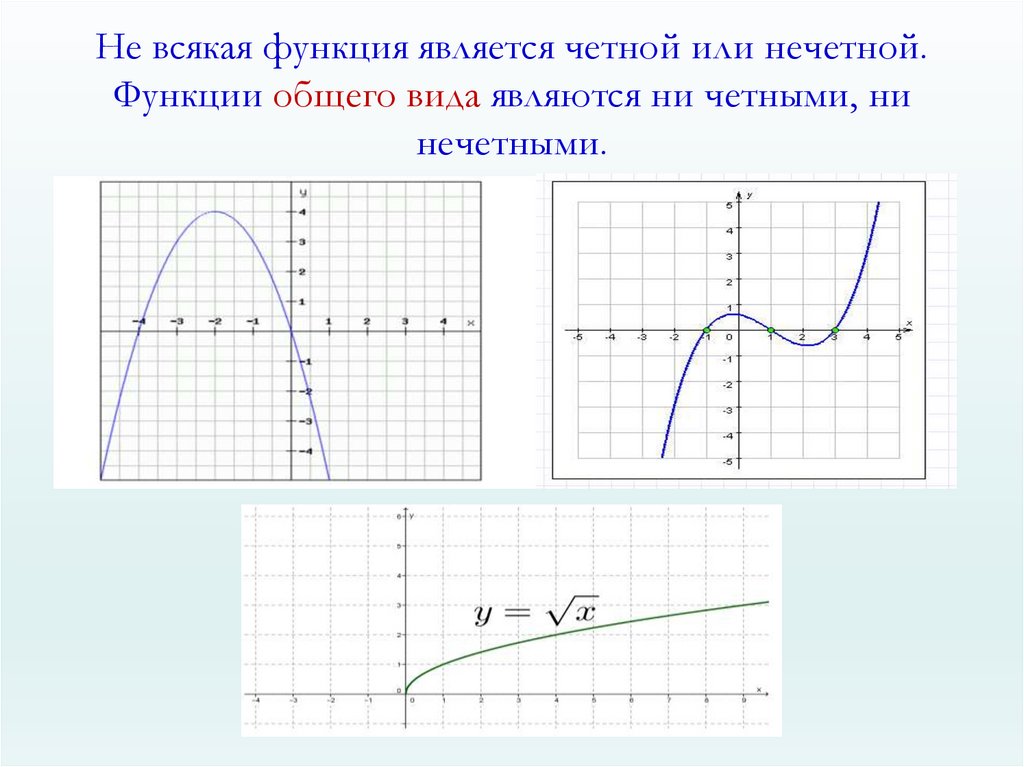
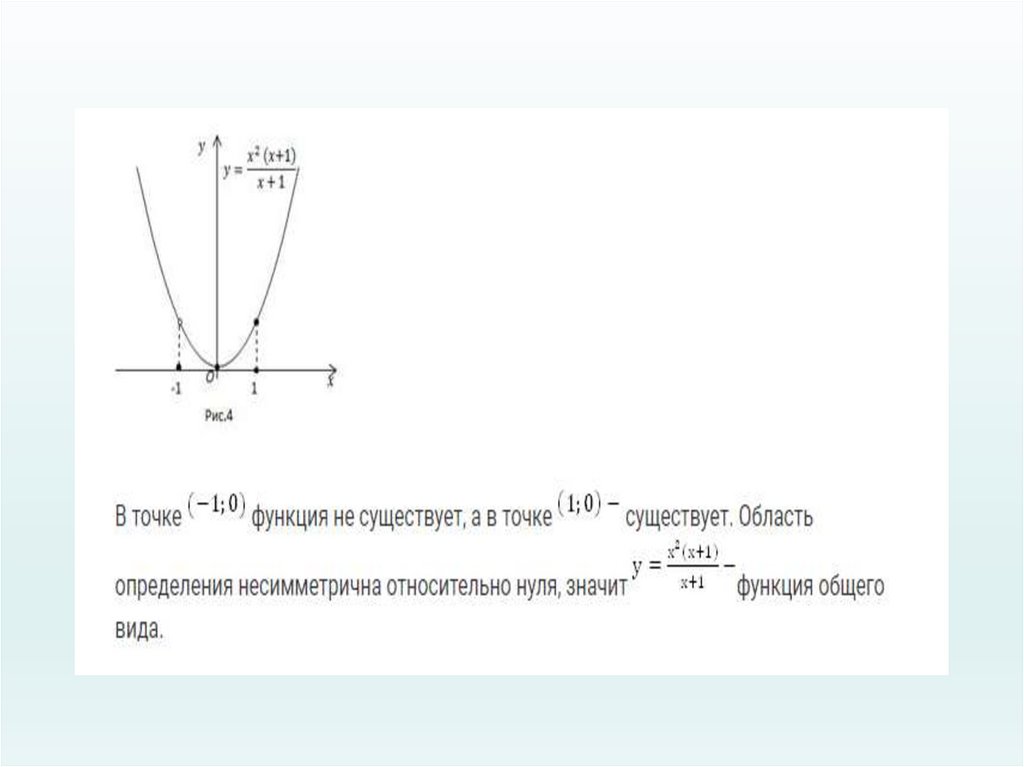
10. Не всякая функция является четной или нечетной. Функции общего вида являются ни четными, ни нечетными.
11.
12.
13.
14.
15.
16.
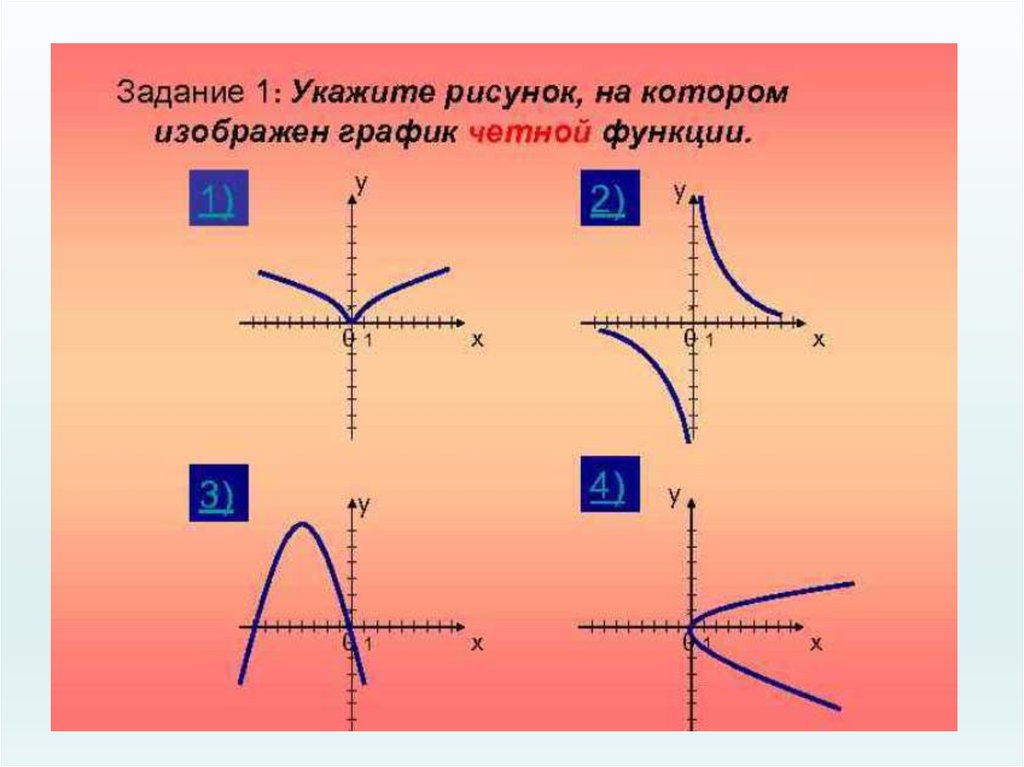
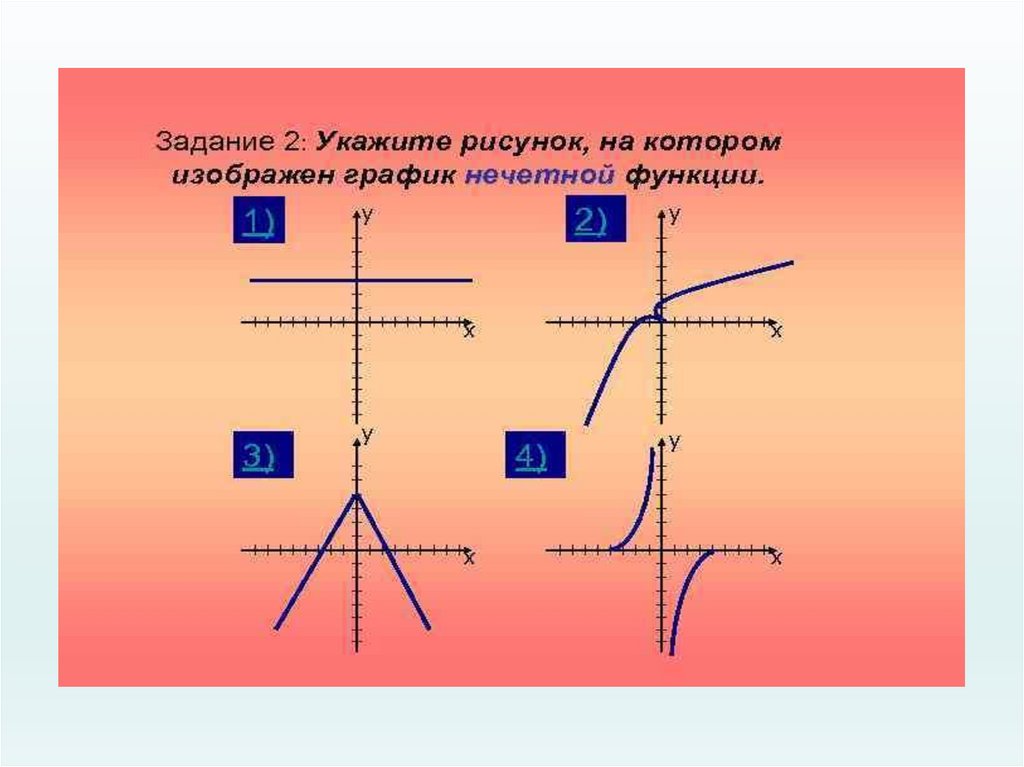
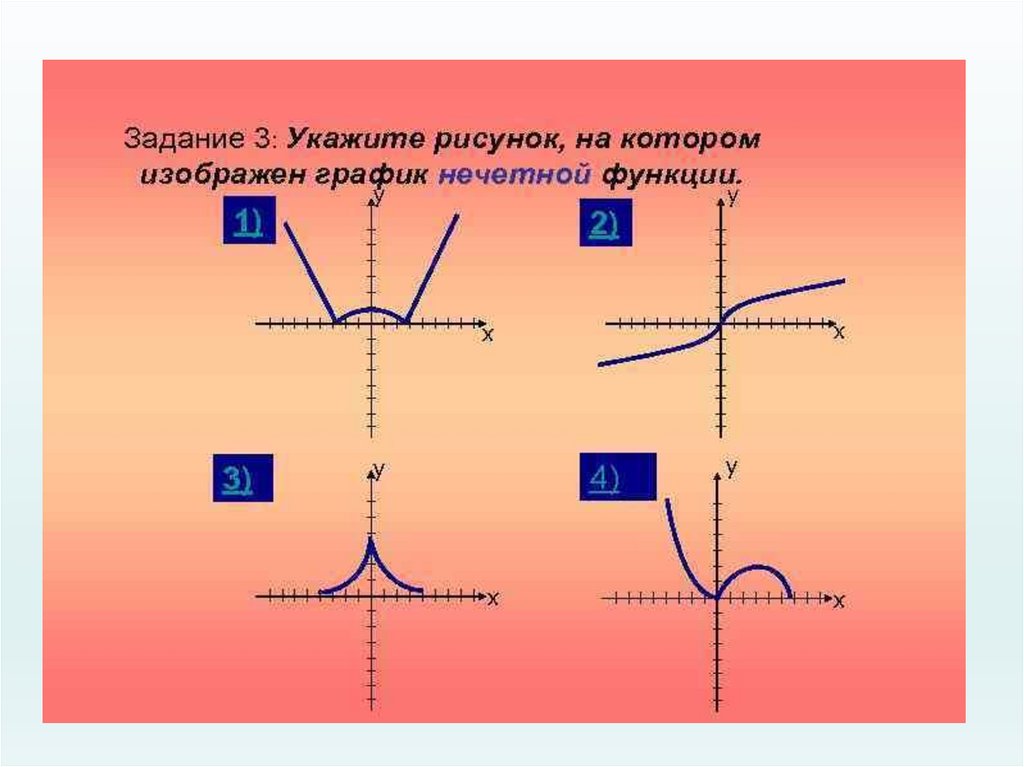
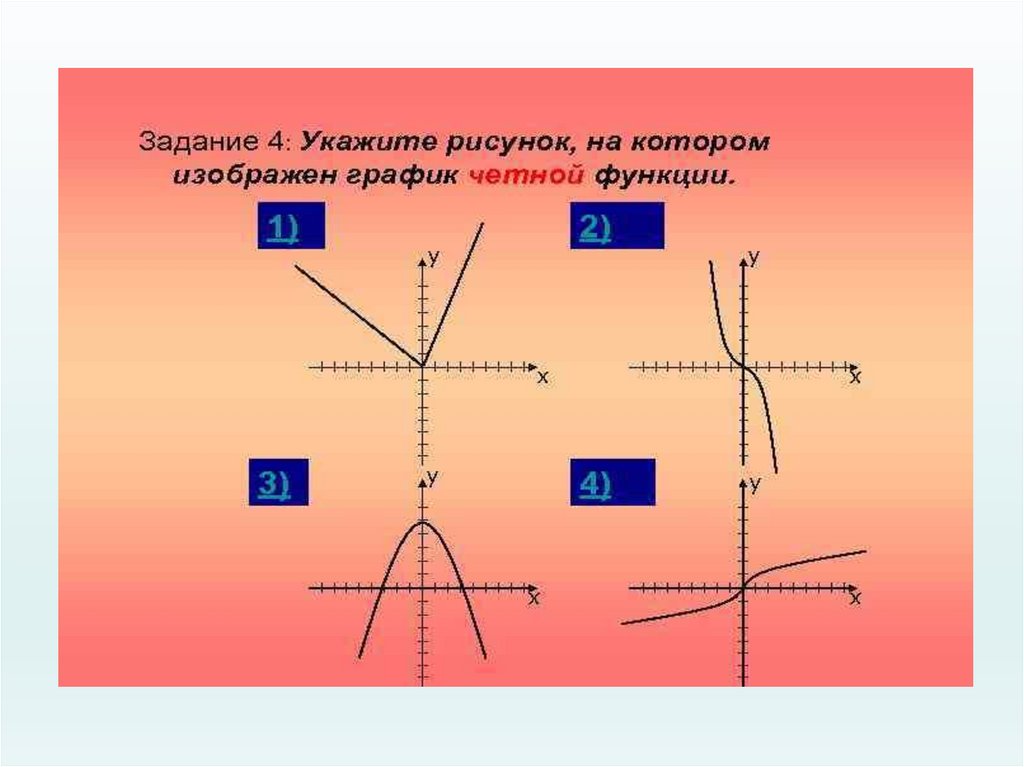
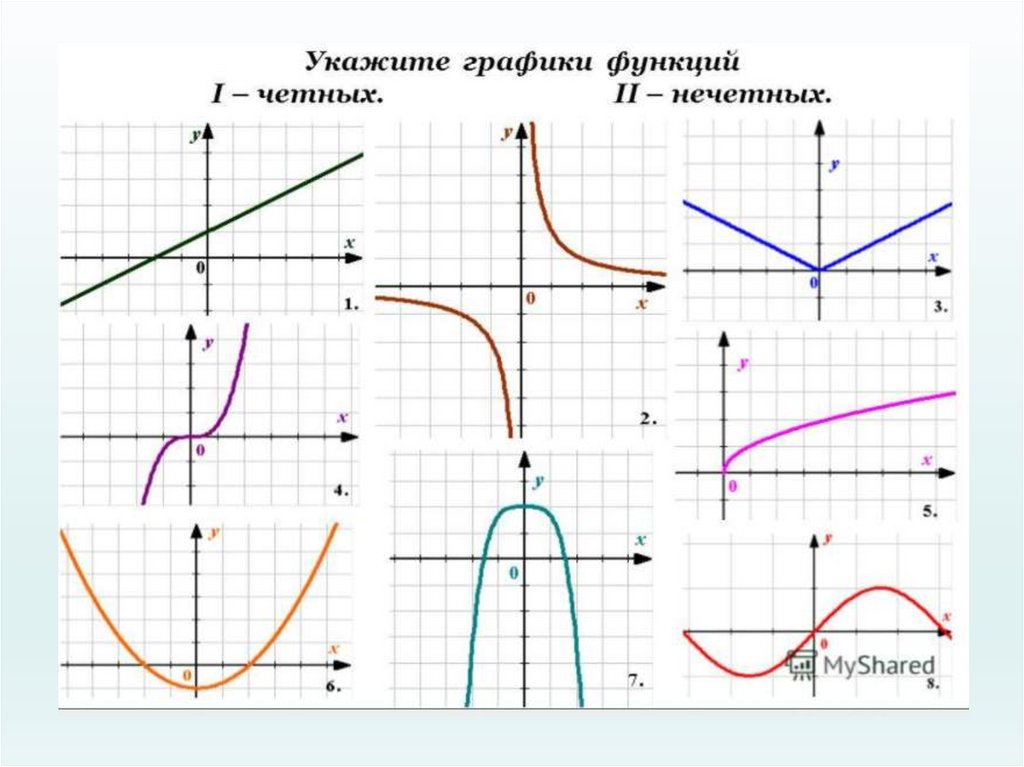
17. Ответь на вопросы:
• Может ли быть чётной или нечётной функция,областью определения которой является:
а) промежуток [ - 2; 5 ] ;
б) промежуток ( - 7; 7 );
в) объединение промежутков [ - 10; - 2 ] U [ 2; 10 ] .
• а) Функция f – чётная, f (3) = 25. Найти f (- 3).
б) Функция f – нечётная, f (- 8) = 71. Найти f (8).
18.
19.
20. Домашнее задание:
Учебник: № 57; № 5821.
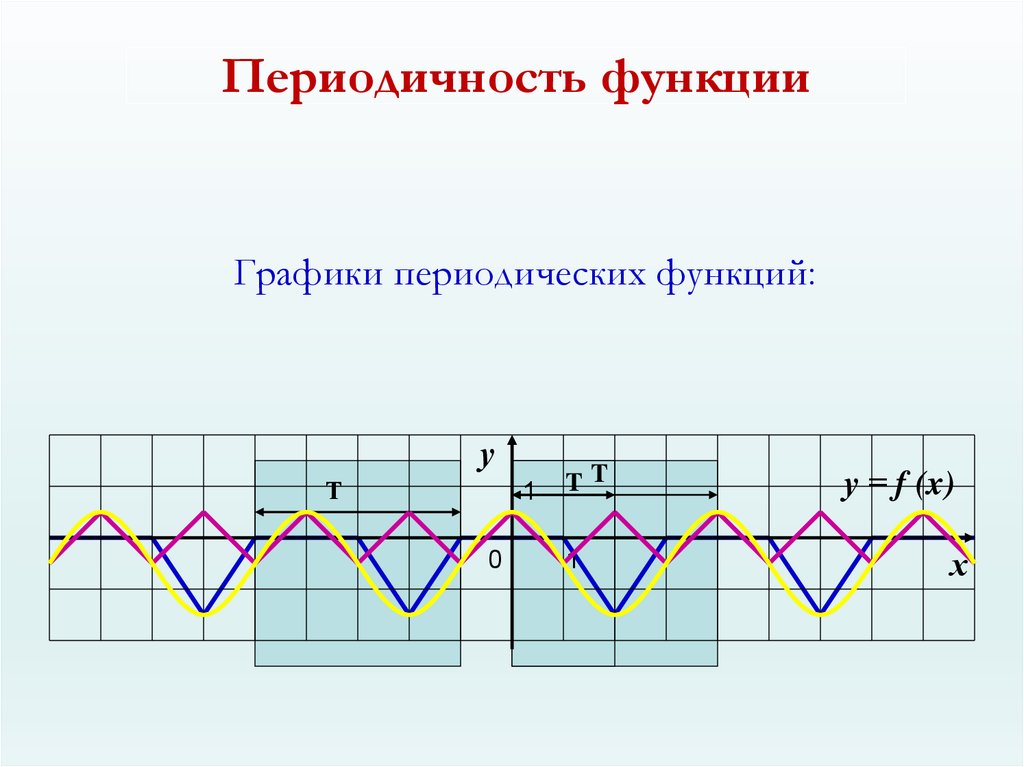
Периодичность функцииГрафики периодических функций:
у
Т
1
0
TT
1
у = f (x)
х
22. Определение
Функция у=f(x) называется периодической , еслисуществует такое отличное от нуля число Т, что для
любого х из области определения этой функции
значения x + T и x – T также принадлежат области
определения и выполняется двойное равенство
f ( x - T) = f(x) = f(x + T)
Т - период функции у=f(x)
23.
У периодической функции бесконечно многопериодов, если Т период, то и 2Т и 3Т и 10Т тоже
периоды, вообще любое число вида: kT, где k- целое
число.
Наименьший положительный период называется
основным периодом.
24.
sin(x+2πk)=sinx, k∈Z.cos(x+2πk)=cosx,k∈Z.
у=sinx, у=cosx — периодические функции с
наименьшим положительным периодом 2π
tg(x+πk)=tgx, k∈Z
ctg(x+πk)=ctgx,k∈Z
у = tgx, у=ctgx— периодические функции с
наименьшим положительным периодом π
25.
Пример №1Найти основной период функции у = sin7x
Решение:
Пусть Т основной период нашей функции, тогда:
sin7x=sin(7(x+Т))=sin(7x+7Т).
мы знаем что 2πk период синуса, найдем решение
нашей задачи:
sin(7x+7Т)= sin(7x+ 2πk)
7t = 2πk
t = 2πk/7
Ответ: T = 2πk/7
26.
Свойство 1.27.
Пример №2.Найти наименьший положительный период функций
28. №62 Докажите, что число Т является периодом функции f, если:
29. № 63 Докажите, что функции являются нечетными: f ( x - T) = f(x) = f(x + T)
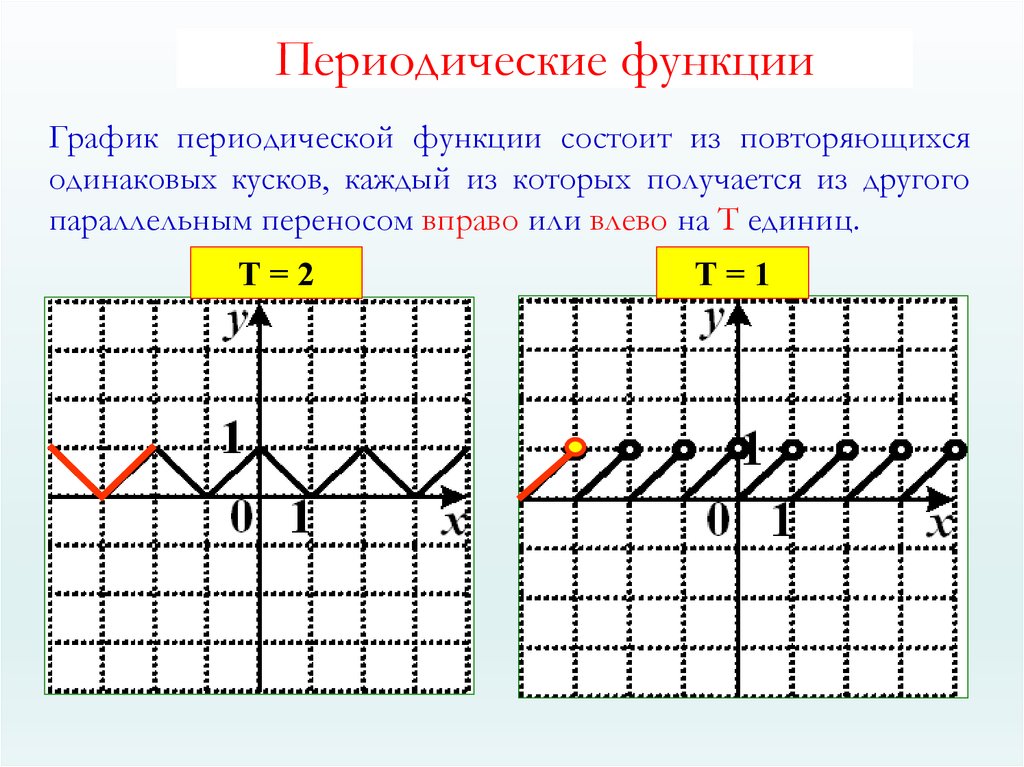
30. Периодические функции
График периодической функции состоит из повторяющихсяодинаковых кусков, каждый из которых получается из другого
параллельным переносом вправо или влево на Т единиц.
Т=2
Т=1
31.
Свойство 2.32.
Пример №3.Найти период функции:

















 mathematics
mathematics








