Similar presentations:
Матрици. Линейна алгебра. Аналитична геометрия
1.
Основни раздели на курса:1. Линейна алгебра
2. Аналитична геометрия
I контролна работа 20 точки
3. Функция на една променлива
Диференциално смятане
Интегрално смятане
II контролна работа 20 точки
3. Функция на две променливи
2.
Матрици1. Основни понятия
Определение:
Правоъгълна таблица с m реда и n стълба – матрица от ред m n
a11 a12
a21 a22
a1n
a2n
am1 am2
amn
aij
aij m n
ij - ти елемент на матрицата
ai1 ai 2
a1 j
a2 j
amj
ain
i - номер на реда на матрицата
j - номер на стълба на матрицата
i - ти ред на матрицата
j - ти стълб на матрицата
– вектор ред
– вектор стълб
3.
Пример:Намерете матрицата
A
2i j , i j
A aij 3 2 ако a
ij
3i j , i j
a11 a12
a21 a22
a31 a32
a11 2.1 1 3
a12 3.1 2 1
a21 3.2 1 5
a22 2.2 2 6
a31 3.3 1 8
a32 3.3 2 7
A
3
5
8
1
6
7
4.
2. Видове матрициАко aij 0 за всяко i , j – нулева матрица
Ако m n – квадратна матрица от ред n
a11 a12
a21 a22
a1n
a2n
an1 an 2
a11 , a22 ,
a1n , a2n 1 ,
a11 a12
a22
0
0
0
, ann
ann
– главен диагонал
– втори диагонал
, an1
a1n
a2n
ann
– горно триъгълна матрица
a11
a21
0
a22
an1 an 2
0
0
ann
– долно триъгълна матрица
5.
a11 0a22
0
0
0
0
ann
0
c
0
0
– диагонална матрица
0
c
0
0
0
c
1
0
0
1
0
0
– скаларна матрица
0
0
1
En
– единична матрица от ред n
6.
a11a21
a12
a22
a1n
a2n
– квадратна матрица от ред n
an1 an 2
ann
Ако aij a ji за всяко i , j – симетрична матрица
Пример:
1
3
3
2
4
7
4
7
5
Ако aij a ji за всяко i, j – антисиметрична матрица
aii aii aii 0
Пример:
0
3
3
0
4
7
4
7
0
7.
3. Действия с матрици– умножение на матрица с число
A
a11 a12
a21 a22
a1n
a2n
am1 am2
amn
– събиране на матрици A, B – еднотипни матрици
A B
a11 b11 a12 b12
a21 b21 a22 b22
a1n b1n
a2n b2n
am1 bm1 am2 bm2
amn bmn
– противоположна матрица A 1 A
1.A A
Свойства: A ( A) O
A O A
A B B A
A B C A B C
O нулева матрица
( A B) A B
( )A A A ,
( ) A ( A)
8.
– умножение на матрици (ред по стълб)Cm p Am n Bn p
n
cij aik bkj ai1b1 j ai 2b2 j
k 1
ainbnj ai1 ai 2
ain
i -ти ред по j -ти стълб
bnj
Свойства:
( AB) ( A) B ( A B)C AC BC
( AB)C A( BC )
– транспониране на матрица
a11 a12
a1n
a21 a22
a2n
Am n
am1 am2
3
2
AT T
A
Свойства:
AnT m
amn
Пример: A2 3 1
3
b1 j
b2 j
4
7
A3 2
AE EA A
a11
a21
am1
a12
a22
am2
a1n
a2n
amn
1 3
3 2
4 7
A B T AT BT
AB T BT AT
9.
Пример:A
Намерете x, y ако AТ B където
2 0
1 5
Т
A
От AТ B следва
B
2 y 2
x 1
5
2 1
0 5
y 2 1
y 3
x 1 0
x 1
10.
Пресметнете: AB, AC, BA, C . AA 1 2 3
2
AB 1 2 3 1 1.2 2.1 3.3 13
1 3.3 1 1 1 3
T
T
2 1
2
B 1 C 1 2
3
3
0
2 1
AC 1 2 3 1 2 1.2 2.1 3.3 1.1 2.( 2) 3.0
3 0
1 3.3 2 1 2
2.1 2.2 2.3 2 4 6
2
BA 1 1 2 3 1.1 1.2 1.3 1 2 3
3.1 3.2 3.3 3 6 9
3
13 3
AB BA
Произведението на матрици
не е комутативно
3 1.1 3 3 3
1
2
1
3
2.1 1.2 3.3
T
T
C .A
2
1 2 0 1.1 ( 2).2 0.3
3
2 3.3 1 2 1
13
3
AC T CT . AT
11.
Пресметнете AB и BA2 0
1 1 1
2 3 0
AB
1 1 2 1 1 2
1 3
2 4.4 2 2 2
2 0
1
2 3 0
1 1
A
1 1 2 1 B
1 2
1
3
2.2 3.1 0.( 1) 1.1 2.0 3.( 1) 0.2 1.3
1.2 1.1 2.( 1) ( 1).1 1.0 1.( 1) 2.2 ( 1).3
0 0
O
0 0
2 0
1 1 2 3 0
1
BA
1 2 1 1 2 1
1 3
2.( 2) 0.1
2.3 0.1
4 2.2 4 4 4
2.0 0.2
AB BA
Произведението на матрици
не е комутативно
2.1 0.( 1)
4 6 0 2
1.( 2) ( 1).1 1.3 ( 1).1 1.0 ( 1).2 1.1 ( 1).( 1) 3 2 2 2
( 1).( 2) 2.1 ( 1).3 2.1 ( 1).0 2.2 ( 1).1 2.( 1)
4 1 4 3
1.( 2) 3.1
1.1 3.( 1)
1.3 3.1
1.0 3.2
1
6
6
2
12.
Пресметнете: f ( A)f ( x) x 3 x 2
2
4 0 1
A 3 2 0
0 1 3
f ( A) A2 3 A 2 E
4 0 1 4 0 1 4 0 1
1 0 0
3 2 0 3 2 0 3 3 2 0 2 0 1 0
0 1 3 0 1 3 0 1 3
0 0 1
4.1 0.0 1.3
4.4 0.( 3) 1.0
4.0 0.( 2) 1.( 1)
( 3).4 ( 2).( 3) 0.0 ( 3).0 ( 2).( 2) 0.( 1) ( 3).1 ( 2).0 0.3
0.4 ( 1).( 3) 3.0
0.0 ( 1).( 2) 3.( 1)
0.1 ( 1).0 3.3
0 3 2 0 0
12
9 6 0 0 2 0
0 3 9
0 0 2
16 1 7
6 4 3
3 1 9
10 0 3 26 1 10
9 8 0 15 4 3
0 3 7 3 4 16
13.
11 Докажете, че матриците са комутативни.
1 1
B
2 1
3
2
Доказваме, че AB BA
3
1
2
1 1.1 ( 1).( 2) 1.1 ( 1).( 1)
1 1
AB
4 1
3 2 1
2
2.1 3.( 2)
2.1 3.( 1)
Задача: A
BA 1
2
1
1
1
2
1.( 1) 1.3
1.1 1.2
3
1
4
( 2).1 ( 1).2 ( 2).( 1) ( 1).3
3
2
1
Задача:
Намерете неизвестната матрица от уравнението (решете матричното уравнение).
1
2 X 0
5
2 1
a
Определяме, че X 2 1 Означаваме X 2 1
b
0
a
0 Получаваме a 2b
1 2
5
Заместваме в уравнението
5
2a b
2 1
b
a 2b 0
2a b 5 2
a 2b 0
4a 2b 10
5a 10
a 2
b 2a 5 1
X
2
1








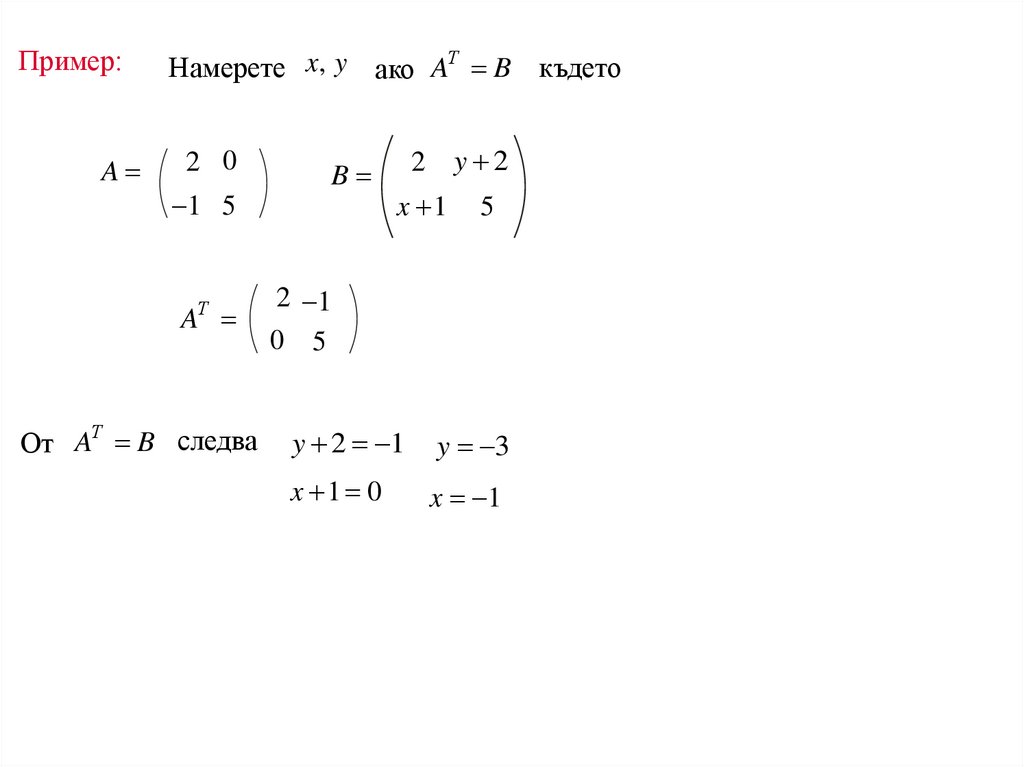




 mathematics
mathematics








