Similar presentations:
Системы линейных уравнений. Ранг матрицы
1. Исследование систем линейных уравнений.
Ранг матрицы2.
Система m линейных уравнений с nпеременными имеет вид:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
.........................................
am1x1 am 2 x2 ... amn xn bm
aij
bi
- коэффициенты системы,
- свободные члены.
Решением системы называется такая
совокупность значений, при подстановке которых
каждое уравнение системы обращается в верное
равенство.
3.
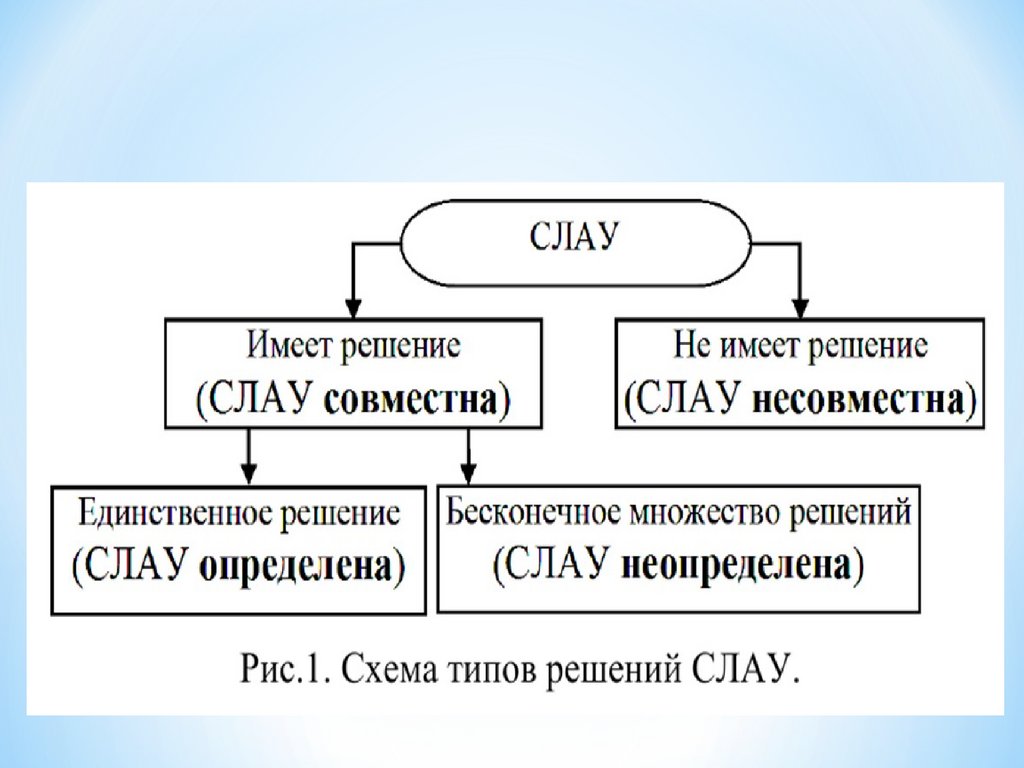
Система линейных уравнений называется:совместной, если она имеет хотя
бы одно решение;
несовместной, если она не имеет
решений;
определенной, если она имеет
единственное решение;
неопределенной, если она имеет
более одного решения;
однородной, если все bi=0;
неоднородной, если не все bi=0.
4.
5. Исследование систем линейных уравнений
Теорема Кронекера - Капелли. Для того, чтобы системалинейных алгебраических уравнений была совместна (имела
решение), необходимо и достаточно, чтобы ранг расширенной
матрицы системы равнялся рангу матрицы коэффициентов:
r ( Ap ) r ( A)
r ( Ap ) r ( A) , то система несовместна (не
Если
имеет решений).
r ( Ap ) r ( A) n
Если
(числу неизвестных), то система
совместна и определенна (имеет единственное решение).
r ( Ap) r ( A) n
Если
, то система совместна
неопределенна (имеет бесконечное множество решений):
и
6.
Рангом матрицы А называетсянаивысший порядок отличных от нуля
миноров этой матрицы
Ранг матрицы А обозначается rang A
или r(A).
Алгоритм нахождения ранга способом
перебора миноров:
1.При наличии хотя бы одного элемента,
отличного от нуля, то ранг матрицы как
минимум равен единице (т.к. есть минор
1-го порядка, который не равен нулю).
7.
2.Далее следует перебор миноров 2-гопорядка. Если все миноры 2-го порядка
равны нулю, то ранг равен единице. При
существовании хотя бы одного не
равного нулю минора 2-го порядка,
необходимо перейти к перебору миноров
3-го порядка, а ранг матрицы, в таком
случае, будет равен минимум двум. И
так далее, по аналогии.
8.
2 3 4 5A 0 2 3 1
0 2 2 4
12 миноров 1 - го порядка – сами элементы.
18 миноров 2 - го порядка, например:
2
3
0 2
4
2
Матрица А имеет 4 минора 3 - его порядка,
например:
Наибольший порядок отличного от нуля минора
этой матрицы равен 3, поэтому: r( A ) 3
3
4
0 2 3 20
0
2
2
9.
Ранг матрицы можно найти:• по определению
• методом окаймляющих миноров
• методом Гаусса (с помощью
элементарных преобразований)
Нахождение ранга матрицы методом Гаусса
— метод, который основывается на теории
эквивалентности матриц: если матрица В
получена из матрицы А при помощи
конечного числа элементарных
преобразований, то r(A) =r(B).
10.
Теорема.Эквивалентные (элементарные)
преобразования не меняют ранга матриц
Суть метода элементарных преобразований:
привести матрицу ,чей ранг необходимо найти,
к трапециевидной при помощи элементарных
преобразований.
11.
Эквивалентные преобразования:Умножение или деление элементов одного ряда на одно
и то же число, не равное нулю
Перестановка местами двух рядов
Прибавление к элементам ряда элементов другого
параллельного
ряда,
умноженного
на
произвольный множитель
Вычеркивание нулевого ряда
12.
Ранг матрицы равен числу ненулевых строк матрицы,приведенной к треугольному виду.
1 3 2
A 0 5 4 ~
1 7 6
1 3 2 ( 2)
~
0 5 4
0 10 8
1 3 2
0 5 4
0 0 0
r ( A ) 2
13.
Алгоритм исследования СЛАУ1.Записываем расширенную матрицу
системы и с помощью элементарных
преобразований приведем ее к
ступенчатому виду.
2. Используя понятие ранга матрицы и
теоремы Кронекера-Капелли определяем
вид системы.
14.
Бесконечное множество решений:r ( Ap) r ( A) n
Система имеет r базисных переменных и n – r свободных
переменных.
Общее решение системы запишется в виде:
x1(t1,..., tn r )
...
xr (t1,..., tn r )
X
t1
...
tn r
Базисные переменные,
зависящие от свободных
переменных
Свободные
переменные
t1 x r 1; t 2 x r 2 ; t n r x n
15.
Пример. Решить систему:Решение
x1
x2
x3
2 x1 2 x2 2 x3 4
x x x 0
1
2
3
3 x1 3 x2 x3 2
x1 x2 3 x3 2
2
:
2
2 2 2 4
1
1
1
2
( 3) 1 1 1
2 2 V
A p 1 1 1 0 ~ 1 1 1 0 V
0 0 2 2
3 3 1 2
~
0 0 4 4
3 3 1 2
~
1 1 3 2
0 0 4
4
1
1
3
2
x1 x2 x3
2
1 1 1
2
1 1 1
r ( Ap) r ( A) 2 совместна
0 0 2 2
0 0 - 2 2
0 0 0
0
r ( Ap ) n неопределенна
0
0 0 0
2 базисных переменных, т.к. r 2 например, x1 , x3
1 свободная переменная, т.к. n r 3 2 1 например, x2 t
Восстановим систему:
x1 1 t
x
2
t
x
1
t
x
t
x
2
1
1
3
3
x2 t
2
x
2
x
1
3
3
x 1
3
16. Однородные системы линейных уравнений
a11 x1 a12 x2 a1n xn 0a x a x a x 0
21 1
22 2
2n n
am1 x1 am 2 x2 amn xn 0
Однородная система всегда имеет решение:
x1 0 x2 0 xn 0
- тривиальное решение.
Оно является единственным решением системы в случае, когда
r ( A) n
Если r ( A)
решений.
n , то система имеет бесконечное множество
17.
Решить однородную систему уравнений:x1 x2 5 x3 7 x4 0
2 x1 x2 4 x3 x4 0
3 x 2 x x 6 x 0
1
2
3
4
1 1 5 7
0 1 14 15
0 1 14 15
1 1 5 7
0 1 14 15
n r 4 2 2
1 1 5 7
1
2 1 4
3 2 1 6
~
1 1 5 7
0 1 14 15
0 0
0
0
r ( A) 2
n 4
( 2)
( 3)
~
( 1)
~
множество решений
- число свободных переменных
















 mathematics
mathematics








