Similar presentations:
Основные положения молекулярно-кинетической теории идеальных газов. Тема 7
1.
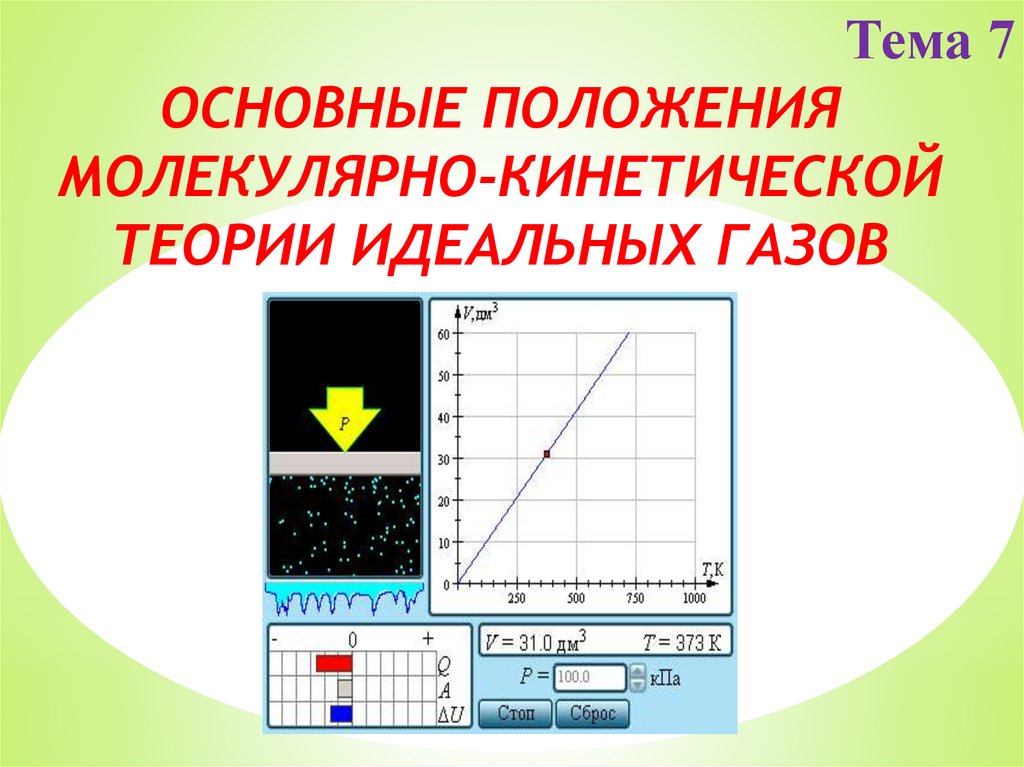
Тема 7ОСНОВНЫЕ ПОЛОЖЕНИЯ
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ
ТЕОРИИ ИДЕАЛЬНЫХ ГАЗОВ
2.
План лекции1. ОСНОВНЫЕ
ПОЛОЖЕНИЯ МОЛЕКУЛЯРНОКИНЕТИЧЕСКОЙ ТЕОРИИ ИДЕАЛЬНЫХ ГАЗОВ (МКТ).
Статистический и термодинамический методы исследований.
2. Силы и потенциальная энергия межмолекулярных взаимодействий.
3. Уравнение состояния идеальных газов.
4. Основное уравнение МКТ идеального газа.
5. Закон Максвелла о распределении молекул идеального газа по
скоростям и энергиям теплового движения. Распределение
Больцмана.
6. Среднее число столкновений и средняя длина свободного пробега
молекул.
3.
ОСНОВНЫЕ ПОЛОЖЕНИЯМОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ИДЕАЛЬНЫХ ГАЗОВ (МКТ).
Статистический и термодинамический методы исследований
Молекулярная физика и термодинамика – разделы физики, в которых изучаются
макроскопические процессы, связанные с огромным числом атомов и молекул,
содержащихся в телах.
Для исследования этих процессов применяют два качественно различных и взаимно
дополняющих друг друга метода:
1)статистический (молекулярно-кинетический),
2)термодинамический.
Первый лежит в основе молекулярной физики, второй - термодинамики.
Молекулярная физика – раздел физики, изучающий строение и
свойства вещества исходя из молекулярно-кинетических
представлений, основывающихся на том, что все тела состоят из
молекул, находящихся в непрерывном хаотическом движении.
Процессы, изучаемые молекулярной физикой, являются
результатом совокупного действия, огромного числа молекул.
Законы поведения огромного числа молекул изучаются –
статистическим методом.
Он основан на том, что свойства макро системы определяются свойствами частиц
системы, особенностями их движения и усредненными значениями динамических
характеристик (например, <V>, <E>).
4.
ОСНОВНЫЕ ПОЛОЖЕНИЯМОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ИДЕАЛЬНЫХ ГАЗОВ (МКТ).
Статистический и термодинамический методы исследований
Термодинамика – раздел физики, изучающий общие свойства макросистем,
находящихся в состоянии термодинамического равновесия и процессы перехода
между этими состояниями. Термодинамика не рассматривает микропроцессы,
которые лежат в основе этих превращений. Термодинамика базируется на двух
началах, которые являются результатом обобщения опытных данных.
Основа термодинамического метода – определение
состояния
термодинамической
системы.
Состояние
термодинамической
системы
обычно
задается
3
параметрами P, T, V. Параметры состояния системы могут
изменяться. Любые изменения хотя бы одного из
термодинамических параметров, называется процессом.
Макросистема
находится
в
термодинамическом
равновесии, если ее состояние с течением времени не
меняется.
5.
Силы и потенциальная энергия межмолекулярного взаимодействияМодель идеального газа, используемая в (МКТ) газов, позволяет описывать поведение
разряженных реальных газов при достаточно высоких температурах и низких P.
Идеальный газ – газ, в котором пренебрегают размерами молекул и взаимодействием
между молекулами, взаимодействие между молекулами абсолютно упругое.
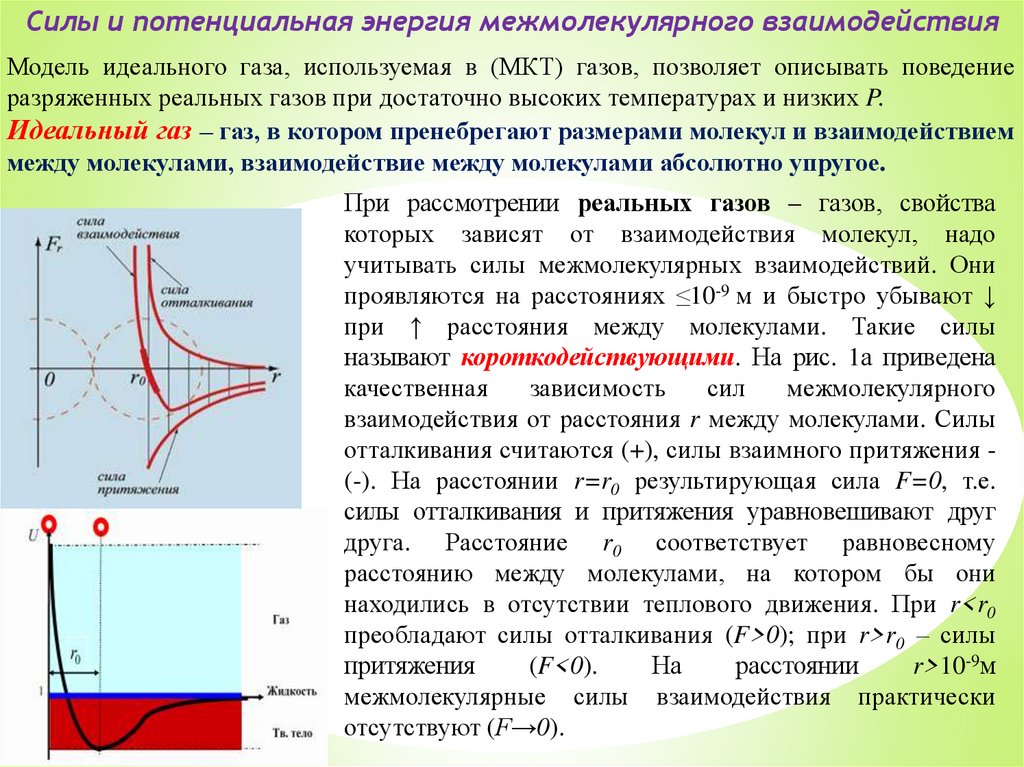
При рассмотрении реальных газов – газов, свойства
которых зависят от взаимодействия молекул, надо
учитывать силы межмолекулярных взаимодействий. Они
проявляются на расстояниях ≤10-9 м и быстро убывают ↓
при ↑ расстояния между молекулами. Такие силы
называют короткодействующими. На рис. 1а приведена
качественная
зависимость
сил
межмолекулярного
взаимодействия от расстояния r между молекулами. Силы
отталкивания считаются (+), силы взаимного притяжения (-). На расстоянии r=r0 результирующая сила F=0, т.е.
силы отталкивания и притяжения уравновешивают друг
друга. Расстояние r0 соответствует равновесному
расстоянию между молекулами, на котором бы они
находились в отсутствии теплового движения. При r<r0
преобладают силы отталкивания (F>0); при r>r0 – силы
притяжения
(F<0).
На
расстоянии
r>10-9м
межмолекулярные силы взаимодействия практически
отсутствуют (F→0).
6.
Силы и потенциальная энергия межмолекулярного взаимодействияКритерием различных агрегатных состояний вещества является соотношение величины
Umin и kT.
Umin – наименьшая потенциальная энергия взаимодействия молекул – определяет работу,
которую нужно совершить против сил притяжения для того, чтобы разъединить
молекулы, находящиеся в равновесии (r=r0),
kT – определяет удвоенную энергию, приходящуюся
на одну степень свободы
i
хаотического теплового движения молекул ( 2 kT ),
R
Дж
1,38 10 23
,
– постоянная
Больцмана,
NA
К
k
R 8,31
1
N A Авогадро,
6,022 10
- число
моль
23
Дж
- универсальная газовая постоянная.
К моль
Если Umin<<kT, то вещество находится в газообразном состоянии, т.к. движение молекул
препятствует соединению молекул.
Если Umin>>kT, то вещество находится в твердом состоянии, т.к. молекулы не могут
удалиться на значительное расстояние и колеблются около положения равновесия.
Если Umin≈kT, то вещество находится в жидком состоянии, т.к. молекулы перемещаются в
пространстве, но не расходятся на расстояние, превышающее r0.
Таким образом, любое вещество в зависимости от температуры может находиться в
газообразном, жидком и твердом состоянии, причем температура перехода из одного
агрегатного состояния в другое зависит от значения Umin для данного вещества.
7.
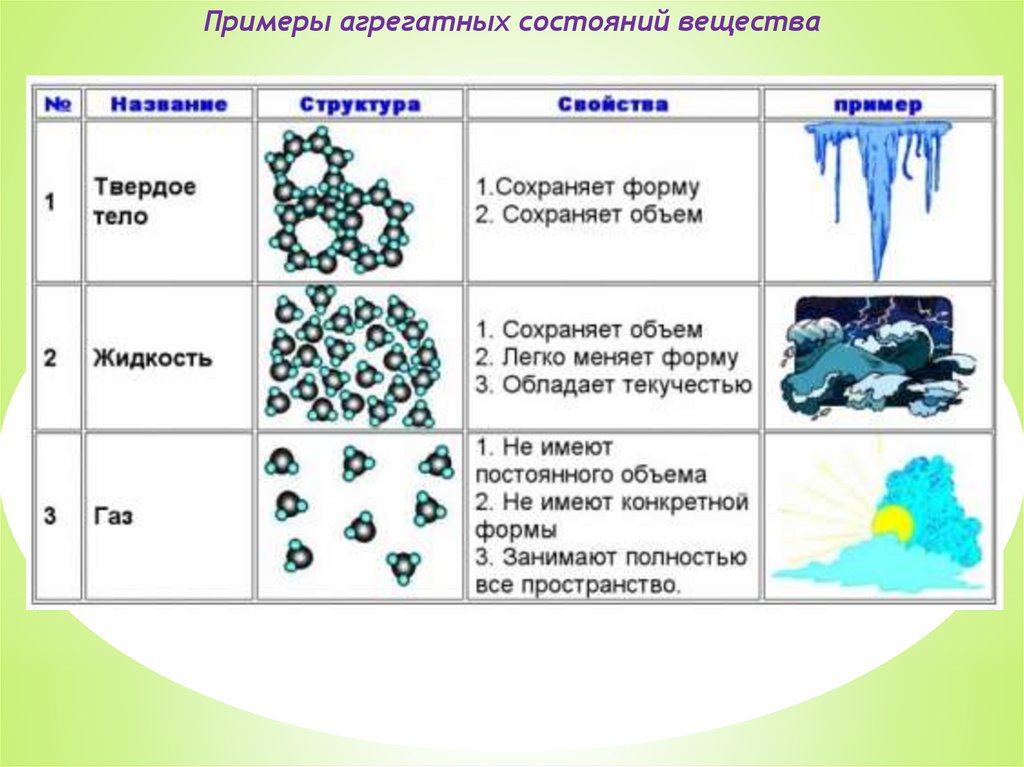
Примеры агрегатных состояний вещества8.
Изотермический процесс (закон Бойля-Мариотта)Еще до появления МКТ опытным путем были установлены законы, описывающие
поведение идеальных газов.
Закон Бойля-Мариотта: для данной массы
газа при T=const, m=const произведение
давления на объем остается величиной
постоянной
PV const. (1)
Рис. 1. Изотермы
Такой процесс называется изотермическим.
Кривая, изображающая зависимость между p и V
при T=const, называется изотермой (рис. 1).
Изотермы представляют собой гиперболы,
расположенные на графике тем выше, чем выше
Т, при которой происходит процесс.
9.
Изобарный процесс (закон Гей-Люссака)Рис. 2. Изобары
Закон Гей-Люссака: объем данной массы газа m=const при P=const
изменяется линейно с температурой
V Vo (1 t ), (2)
V0 – объем при 00С.
Процесс, протекающий при P=const, называется изобарным.
На диаграмме в координатах V, t изобарный процесс изображается
прямой - изобарой (рис. 2).
10.
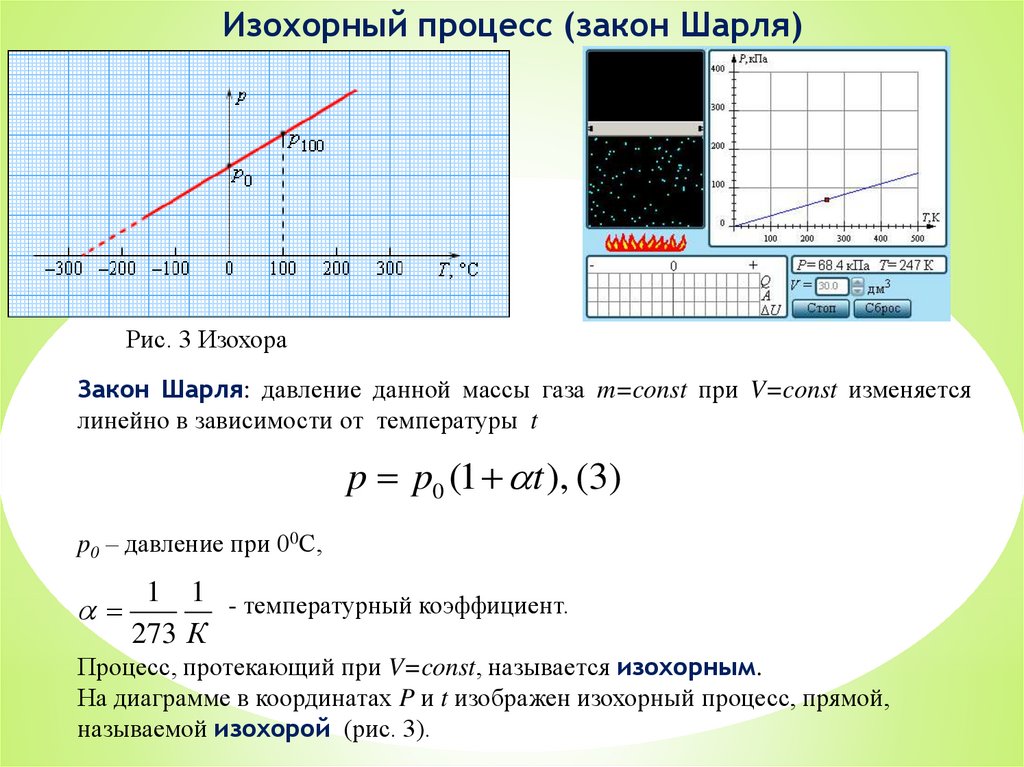
Изохорный процесс (закон Шарля)Рис. 3 Изохора
Закон Шарля: давление данной массы газа m=const при V=const изменяется
линейно в зависимости от температуры t
p p0 (1 t ), (3)
p0 – давление при 00С,
1 1 - температурный коэффициент.
273 К
Процесс, протекающий при V=const, называется изохорным.
На диаграмме в координатах P и t изображен изохорный процесс, прямой,
называемой изохорой (рис. 3).
11.
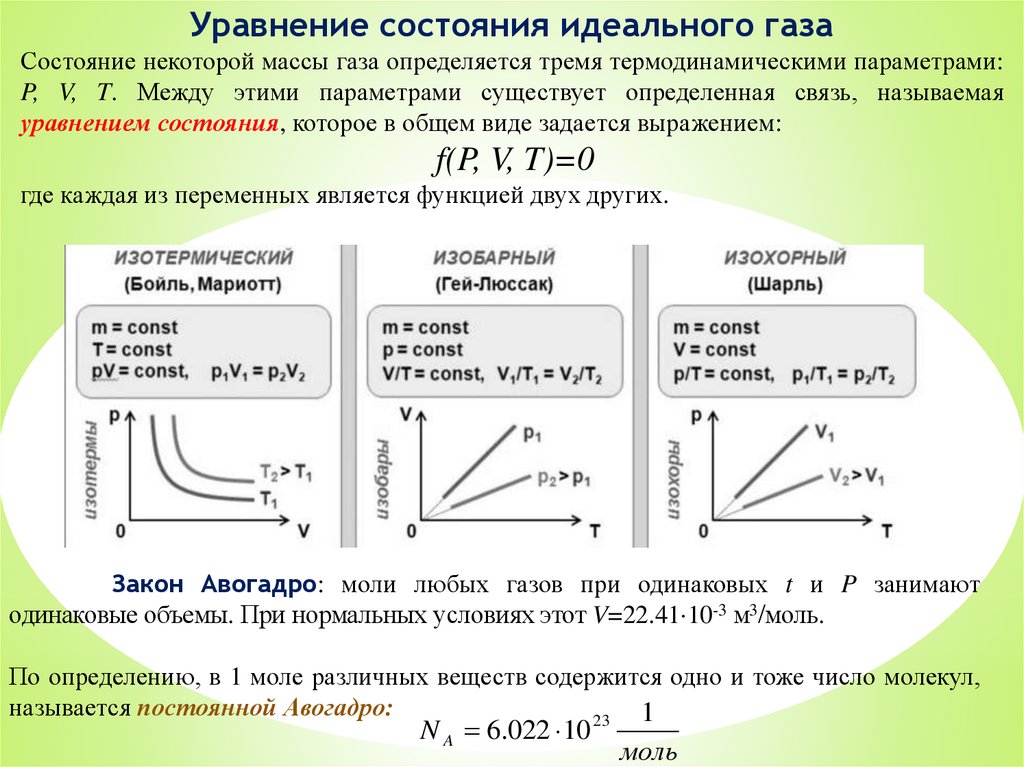
Уравнение состояния идеального газаСостояние некоторой массы газа определяется тремя термодинамическими параметрами:
P, V, T. Между этими параметрами существует определенная связь, называемая
уравнением состояния, которое в общем виде задается выражением:
f(P, V, T)=0
где каждая из переменных является функцией двух других.
Закон Авогадро: моли любых газов при одинаковых t и P занимают
одинаковые объемы. При нормальных условиях этот V=22.41 10-3 м3/моль.
По определению, в 1 моле различных веществ содержится одно и тоже число молекул,
называется постоянной Авогадро:
1
23
N A 6.022 10
моль
12.
Уравнение состояния идеального газаСостояние некоторой массы газа определяется тремя термодинамическими параметрами: P,
V, T. Между этими параметрами существует определенная связь, называемая уравнением
состояния, которое в общем виде задается выражением:
f(P, V, T)=0
где каждая из переменных является функцией двух других.
Французский физик и инженер Б. Клапейрон (1799-1864) получил уравнение состояния
идеального газа, объединив законы Бойля - Мариотта и Гей-Люссака:
PV
B const. (4)
T
Выражение (4) является уравнением Клапейрона, в которых В – газовая постоянная,
различная для разных газов.
Русский ученый Д.И. Менделеев (1834 - 1907) объединил уравнение Клапейрона и закон
Авогадро. Согласно закону Авогадро, при одинаковых P и T моли всех газов занимают
одинаковый молярный объем Vm, поэтому газовая постоянная В будет одинаковой для всех
газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой
постоянной.
Уравнению
Дж
PVм RT . (5)
R 8,31
моль К
удовлетворяет лишь идеальный газ, и оно называется уравнением состояния идеального
газа или уравнением Клапейрона – Менделеева.
13.
Уравнение состояния идеального газаУравнение Клапейрона - Менделеева для массы m газа:
PV
m
RT RT , (6)
m
- количество вещества.
Часто используют другую формулу уравнения Клапейрона-Менделеева, вводя постоянную
Больцмана
R
23 Дж
k
NA
1,38 10
Тогда уравнение Клапейрона - Менделеева
p nkT (7)
NA
n концентрация молекул.
VM
Из (7) следует, что давление для
идеального
газа
при
данной
температуре прямо пропорционально
концентрации его молекул (или
плотности газа). При одинаковых T и
P все газы содержат в единице объема
одинаковое число молекул.
К
,
р
RT kN AT
nkT ,
VM
VM
14.
Основное уравнение МКТ идеальных газовРассмотрим одноатомный идеальный газ. Предположим,
что молекулы газа движутся хаотически, число взаимных
столкновений между молекулами газа пренебрежимо мало
по сравнению с числом ударов о стенки сосуда, а
соударения молекул со стенками сосуда абсолютно упругие.
Выделим на стенке сосуда элементарную площадку ΔS (рис.
4) и вычислим давление, оказываемое на эту площадку. При
каждом
соударении
молекула,
движущаяся
Рис. 4
перпендикулярно площади ΔS, передает ей импульс
m ( m ) 2m ,
где m0 – масса молекулы; – скорость молекулы.
За время Δt площадки достигнут только те молекулы, которые заключены в объеме
цилиндра с основанием ΔS и высотой Δt. Число этих молекул равно N nV n S t ,
где n – концентрация молекул.
1
Число ударов молекул, движущихся в одном направлении, о площадку ΔS:
N1 n S t.
6
При столкновении с площадкой они передадут ей импульс:
0
0
0
1
1
Δp 2m0 nΔS Δt nm0 2 ΔSΔt.
6
3
Тогда давление газа, оказываемое им на стенку сосуда:
Р
Δp
1
nm0 2 , (8)
ΔtΔS 3
15.
Основное уравнение МКТ идеальных газовЕсли газ в объеме V содержит N молекул, движущихся со скоростями 1, 2,…, n, то
N
целесообразно рассмотреть среднюю квадратичную скорость:
2
i
которая характеризует всю совокупность молекул газа.
КВ i 1 , (9)
Уравнение (8) с учетом (9):
N
1
3
2
- основноеpуравнение
идеальных
газов.
nm0 КВМКТ
. (10
)
КВ
3RT
, (11)
КВ
3RT
3kT
, (12)
m0 N A
m0
m0 N A , m - масса молекулы газа.
o
Средняя кинетическая энергия поступательного движения 1 молекулы идеального газа
0
E m
0 КВ
N
2
2
3
kT . (13)
2
Средняя кинетическая энергия поступательного движения молекулы идеального газа
пропорциональна температуре и зависит только от нее.
Из уравнения (13) следует, что при T=0 K, < o>=0, т.е. при T=0 К прекращается
поступательное движение молекул газа, следовательно, его p=0.
Таким образом, термодинамическая температура является мерой средней кинетической
энергии поступательного движения молекул идеального газа и формула (13) раскрывает
молекулярно-кинетическое толкование температуры.
16.
Закон Максвелла о распределении молекул идеальногогаза по скоростям и энергиям теплового движения
В газе, находящемся в состоянии равновесия, устанавливается некоторое
стационарное, не меняющееся со временем распределение молекул по скоростям,
которое подчиняется статистическому закону, который теоретически вывел Дж.
Максвелл. Закон Максвелла описывается некоторой функцией f(v), называемой
функцией распределения молекул по скоростям, которую Максвелл нашел,
применяя методы теории вероятностей
2
mo
m
2
o
f ( ) 4
exp
, (1)
2 kT
2kT
3/ 2
Рис. 5
График функции распределения молекул
по скоростям
Из (1) видно, что конкретный вид
функции зависит от рода газа (от массы
молекулы) и от параметра состояния (от
температуры).
График
функции
(1)
представлен на рис. 5.
17.
Закон Максвелла о распределении молекул идеальногогаза по скоростям и энергиям теплового движения
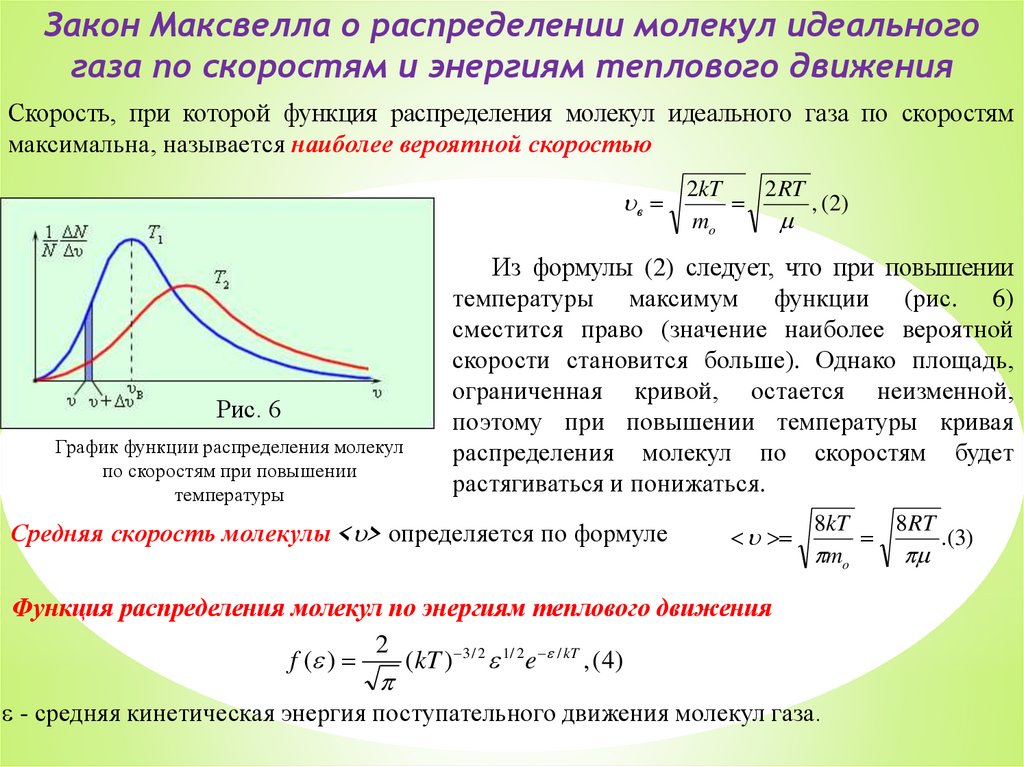
Скорость, при которой функция распределения молекул идеального газа по скоростям
максимальна, называется наиболее вероятной скоростью
в
Рис. 6
График функции распределения молекул
по скоростям при повышении
температуры
2kT
2 RT
, (2)
mo
Из формулы (2) следует, что при повышении
температуры максимум функции (рис. 6)
сместится право (значение наиболее вероятной
скорости становится больше). Однако площадь,
ограниченная кривой, остается неизменной,
поэтому при повышении температуры кривая
распределения молекул по скоростям будет
растягиваться и понижаться.
Средняя скорость молекулы < > определяется по формуле
8kT
8 RT
.(3)
mo
Функция распределения молекул по энергиям теплового движения
2
f ( )
(kT ) 3 / 2 1/ 2 e / kT , (4)
- средняя кинетическая энергия поступательного движения молекул газа.
18.
Закон изменения давления с высотой, предполагая, что поле тяготения однородно,температура постоянна и масса всех молекул одинакова, если атмосферное давление на
высоте h равно p имеет вид
g (h2 h1 )
p2 p1 exp
, (5)
- барометрическая формула
RT
где изменение высоты от h1 до h2 приводит к изменению давления от р1 до р2.
(5) позволяет найти атмосферное давление в зависимости от высоты или, измерив,
давление, найти высоту. Так как высоты обозначаются относительно уровня моря, где
давление считается нормальным, то (5) можно записать
gh
p pо exp
, (6)
RT
где р - давление на высоте h.
Используя формулу p=nkT, можно получить формулу для концентрации молекул на высоте
h, которая называется распределением Больцмана для внешнего потенциального
поля:
n no exp[ mo gh / kT ], (7)
no – концентрация молекул на высоте h=0.
Из (7) следует, что при постоянной температуре плотность газа больше там, где
меньше потенциальная энергия его молекул. Распределение Больцмана справедливо в
любом внешнем потенциальном поле, а не только в поле сил тяжести.
19.
Среднее число столкновенийи средняя длина свободного пробега молекул
Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются
друг с другом. Между двумя последовательными столкновениями молекулы проходят
некоторый путь l, который называется длиной свободного пробега.
В общем случае длина пути между последующими столкновениями различна, но т.к. мы
имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то
говорят о средней длине свободного пробега молекул <l>.
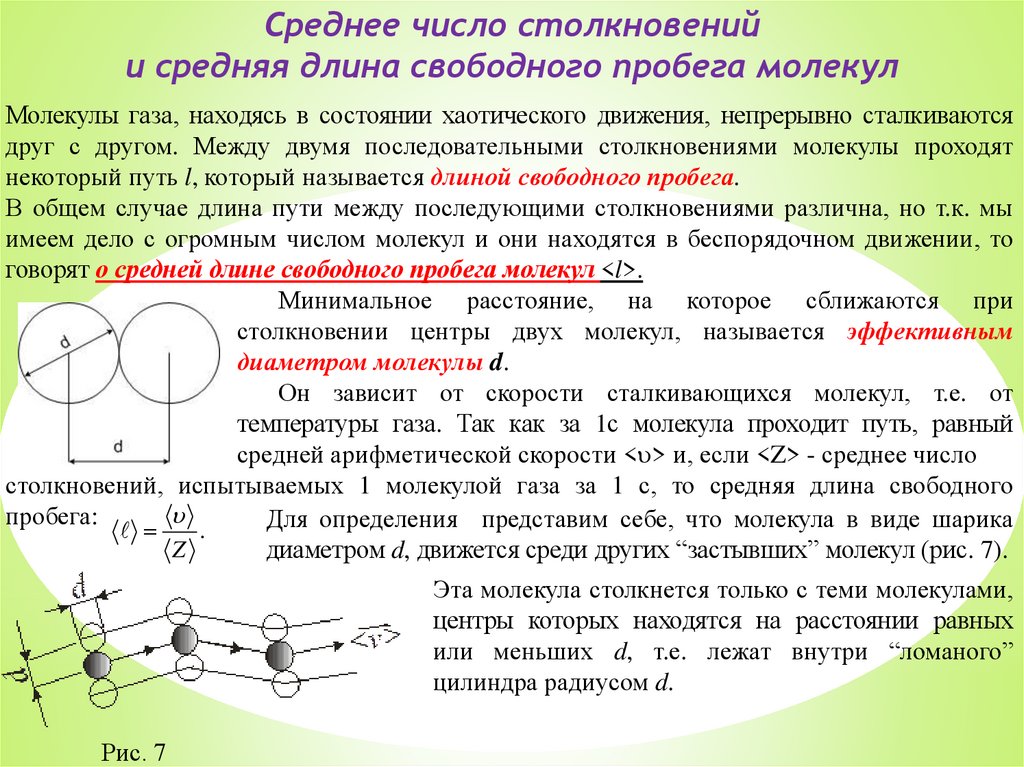
Минимальное расстояние, на которое сближаются при
столкновении центры двух молекул, называется эффективным
диаметром молекулы d.
Он зависит от скорости сталкивающихся молекул, т.е. от
температуры газа. Так как за 1с молекула проходит путь, равный
средней арифметической скорости < > и, если <Z> - среднее число
столкновений, испытываемых 1 молекулой газа за 1 с, то средняя длина свободного
пробега:
Для определения представим себе, что молекула в виде шарика
.
Z
диаметром d, движется среди других “застывших” молекул (рис. 7).
Эта молекула столкнется только с теми молекулами,
центры которых находятся на расстоянии равных
или меньших d, т.е. лежат внутри “ломаного”
цилиндра радиусом d.
Рис. 7
20.
Среднее число столкновенийи средняя длина свободного пробега молекул
Среднее число столкновений за 1с равно числу молекул в объеме “ломаного” цилиндра:
Z nV ,
V d 2 < >
,
- средняя скорость молекулы или путь,
n - концентрация молекул,
пройденный ею за 1с.
Среднее число столкновений:
Z 2 d 2 n .
Тогда средняя длина свободного пробега:
С другой стороны с учетом формулы
следует, что при T=const, n P.
Следовательно,
1
2
n2 p 2
.
n1
p1
p nkT ,
1
2 d 2 n
,
1
т.е. .
n













 physics
physics








