Similar presentations:
Решение линейных уравнений и их систем
1.
Решение линейныхуравнений и их систем
2.
Уравнение с одним неизвестным, которое послераскрытия скобок и приведения подобных членов
принимает вид
aх + b = 0, где a и b произвольные числа,
называется линейным уравнением с одним
неизвестным.
3.
Значение неизвестного, обращающее уравнение вверное
равенство
называется решением или корнем уравнения.
Например, если в уравнении 3х + 7 = 13 вместо
неизвестного х подставить число 2 , то получим
верное равенство 3· 2 +7 = 13. Значит, значение х =
2 есть решение или корень уравнения.
4.
ПримерРешите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х
‒ 1.
Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.
Сгруппируем в левой части члены,
содержащие неизвестные, а в правой ‒
свободные члены:
5х – 3х ‒ 2х = – 12 ‒ 1 + 15 ‒ 2.
Приведем подобные члены:
0х = 0.
Ответ: х - любое число.
5.
6.
Пусть надо решить уравнение1) Умножим все члены уравнения на наименьшее общее кратное
знаменателей, равное 12.
2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)
3) Чтобы отделить члены, содержащие неизвестные и свободные
члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .
4) Сгруппируем в одной части члены, содержащие неизвестные, а в
другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.
5) Приведем подобные члены:
‒ 22х = ‒ 154.
6) Разделим на – 22 , Получим х = 7.
7.
Вообще такие уравнения можно решать последующей схеме:
а) привести уравнение к целому виду;
б) раскрыть скобки;
в) сгруппировать члены, содержащие неизвестное, в
одной части уравнения, а свободные члены ‒ в
другой;
г) привести подобные члены;
д) решить уравнение вида aх = b, которое получили
после приведения подобных членов.
8.
1) 2х = 1/4.2) 2 (х + 3) = 5 – 6х.
3) – 6 (5 – 3х) = 8х – 7
4) 12−(1−6x)x=3x(2x−1)+2x
5) 8(2x−1)−5(3x+0,8)=x−4
6) (7x+1)(3x−1)−21x=3
7) (1−4x)(1−3x)=6x(2x−1)
8) (2x+1)(2x−3)4=x2−1
9.
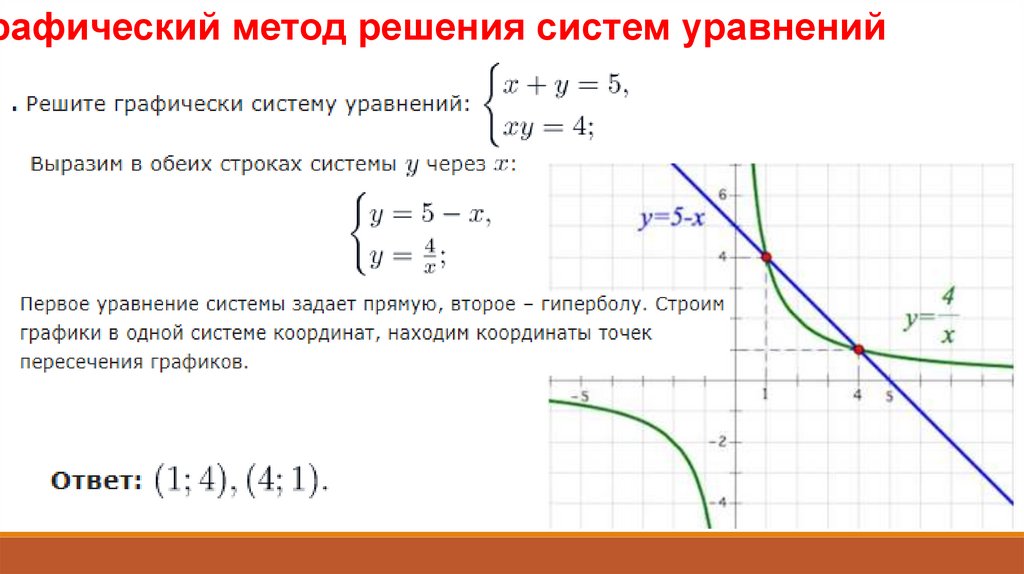
Методы решениясистем уравнений
10.
Системой уравнений называют два уравнения сдвумя неизвестными (чаще всего неизвестные в
них называют «x» и «y»), которые объединены в
общую систему фигурной скобкой.
Чтобы решить систему уравнений, нужно найти и «x»,
и «y».
Существуют два основных способа решения систем
уравнений. Рассмотрим оба способа решения.
11.
Метод подстановки• Выражаем одну переменную через другую.
• Выраженную из одного уравнения переменную
подставляем во второе уравнение. Получаем уравнение
относительно одной переменной, которое и решаем.
• Опираясь на найденное значение одной переменной,
находим значение второй, подставляя в оставшееся
уравнение.
12.
13.
Метод сложения• Добиваемся, путем равносильных преобразований,
наличия равных (или противоположных) коэффициентов
при одной из неизвестных переменных в уравнениях.
• Вычитаем (или складываем) полученные уравнения с
целью выхода на уравнение с одной неизвестной.
• Решаем полученное уравнение с одной неизвестной.
• Найденное значение одной переменной подставляем в
любое из уравнений системы, находим значение второй.







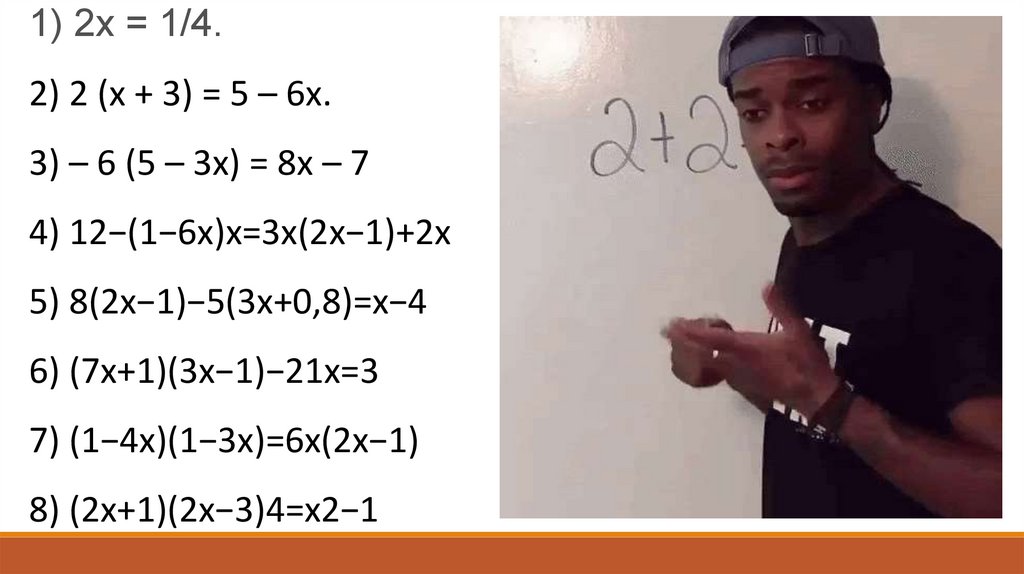








 mathematics
mathematics








