Similar presentations:
Решение систем линейных уравнений методом сложения
1. Алгебра 7 класс
Тема урока:Решение систем линейных
уравнений
методом сложения.
2. Цель урока:
• Научиться решать системы двухлинейных уравнений с двумя
переменными методом
алгебраического сложения.
3. Повторение:
• 1.Что называется системой двухлинейных уравнений с двумя
переменными?
• 2.Что называется решением
системы?
4.
Сколько решений имеет система?a)
2х + у = -3,
3х + у = 1
y = -2x-3,
у = -3x+1
б)
2у =4x+8,
-2х + у = 1
y = 2x+4,
у = 2x+1
в)
2х – 2у = 1,
6х – 6у = 3
y=х – 0.5,
y=х – 0.5
5.
Задача:Четыре медвежонка тяжелее
медведицы на 30 кг, а два таких же
медвежонка легче медведицы на
80 кг. Найти массу медведицы.
Решение:
Пуст ь Х кг – масса медведицы,
У кг – масса одного медвежонка.
Составьте по условию задачи
систему уравнений.
6.
4y-x = 30,х -2у = 80
x = 190, у = 55
Ответ: 190 кг.
7.
+4y-x = 30,
х -2у = 80
(4y-x)+ (х -2у) = 30+80
4y-x+ х -2у = 110
2y = 110
Y = 55
x-2*55 = 80
x = 80+110
x = 190
(190,55)
8. Решить систему:
2х+3у=1,5х+3у=7
9.
-2х+3у=1
5х+3у=7
(2х+3у)-(5х+3у)=1-7
2х + 3у - 5х - 3у = -6
-3х = -6
х=2
2*2+3у = 1
4+3у = 1
3у = -3 у = -1
Ответ: (2;-1)
10. Решить систему:
4х+5у=1,5х+7у=5
11.
4х+5у=1, *55х+7у=5 *4
-
20х+25у=5,
20х+28у=20
-3у=-15,
у= 5.
4х+5*5=1,
4x = -24, x = -6
(-6;5)
12.
Алгоритм метода сложения1)
2)
3)
4)
5)
Привести уравнения системы к одинаковым
по модулю коэффициентам при
переменных x и y.
Если коэффициенты одинаковы, то из
одного уравнения вычесть другое.
Если же коэффициенты противоположные,
то уравнения складываются.
Решить полученное уравнение (найти
значение одной из переменных системы).
Подставить известное значение переменной
в одно из уравнений и найти значение
второй переменной.
Записать ответ.
13.
Исключить одну из переменныхa)
2х + у = -3,
3х + у = 1
б)
2x-y =5,
х + у = 7
в)
5х – 2у =26,
3х + 5у =-3
14.
64
3
2
-5
-2
0
2
4






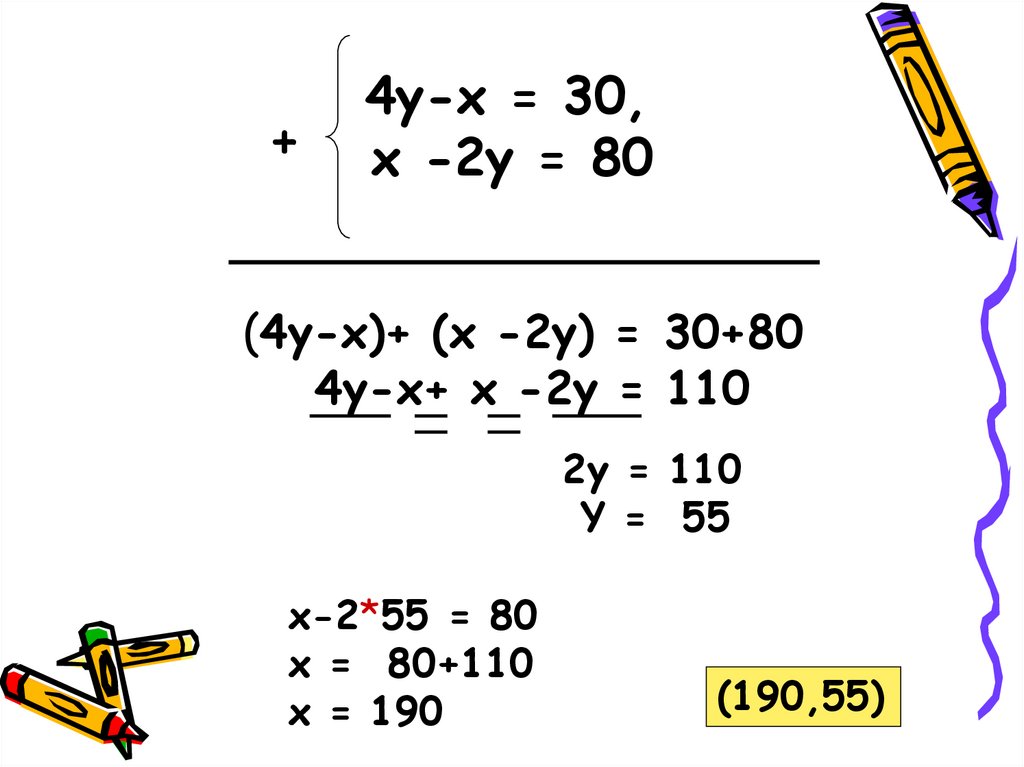


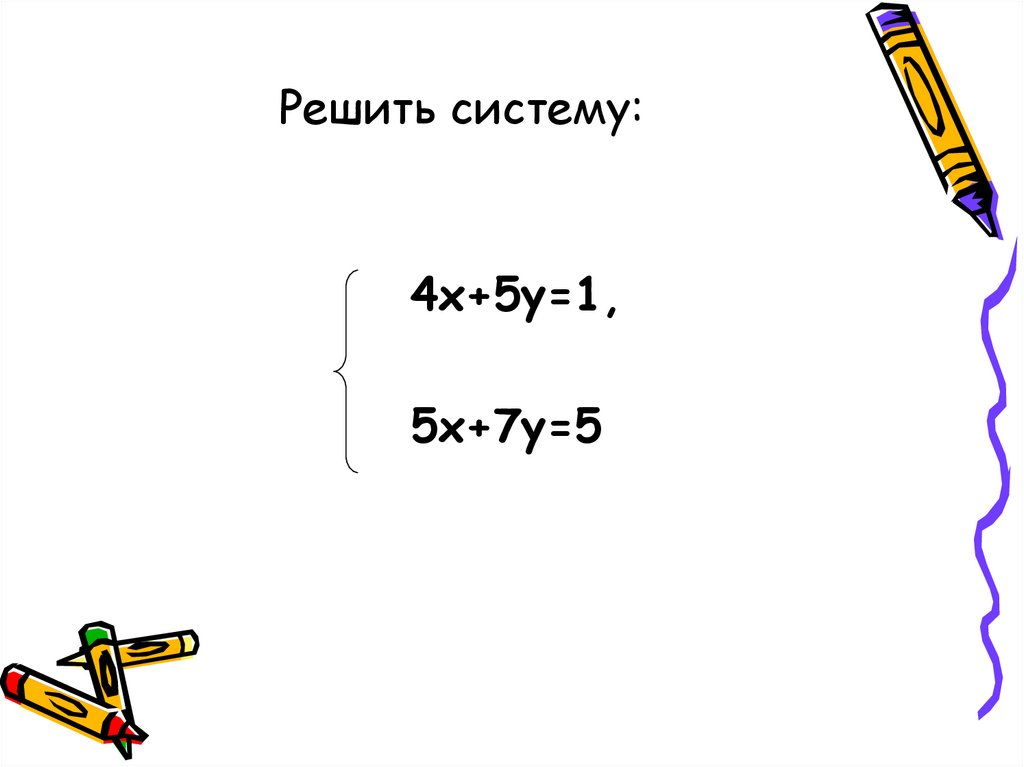
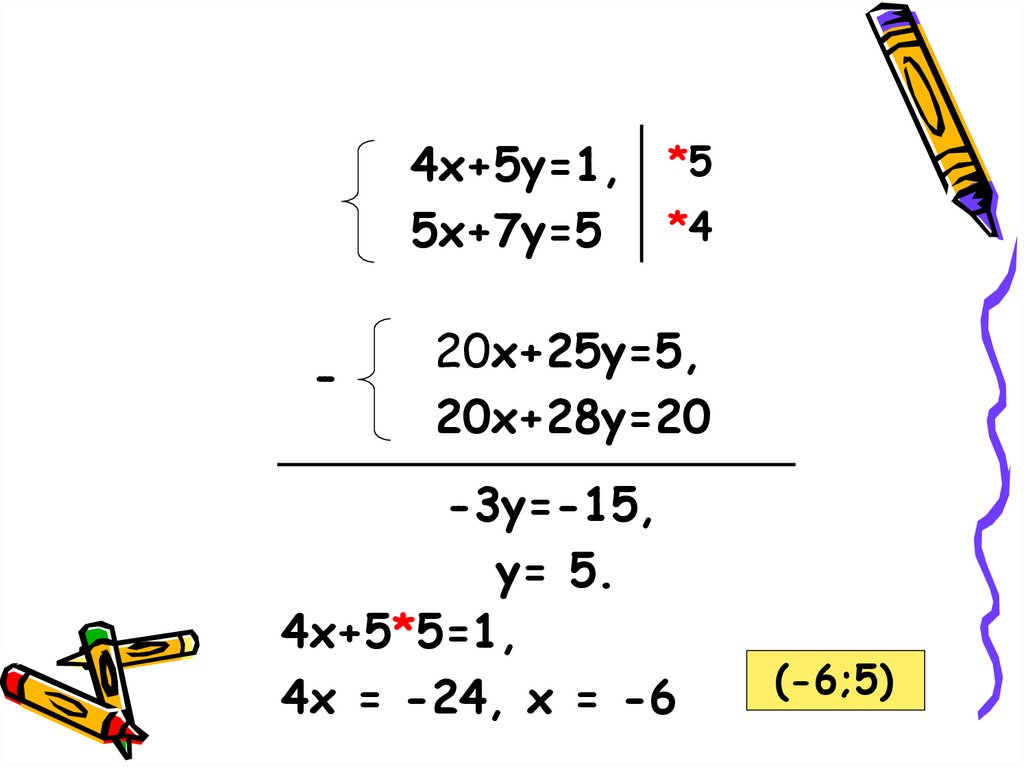



 mathematics
mathematics








