Similar presentations:
Теорема Гаусса
1.
ТЕОРЕМАГАУССА
2.
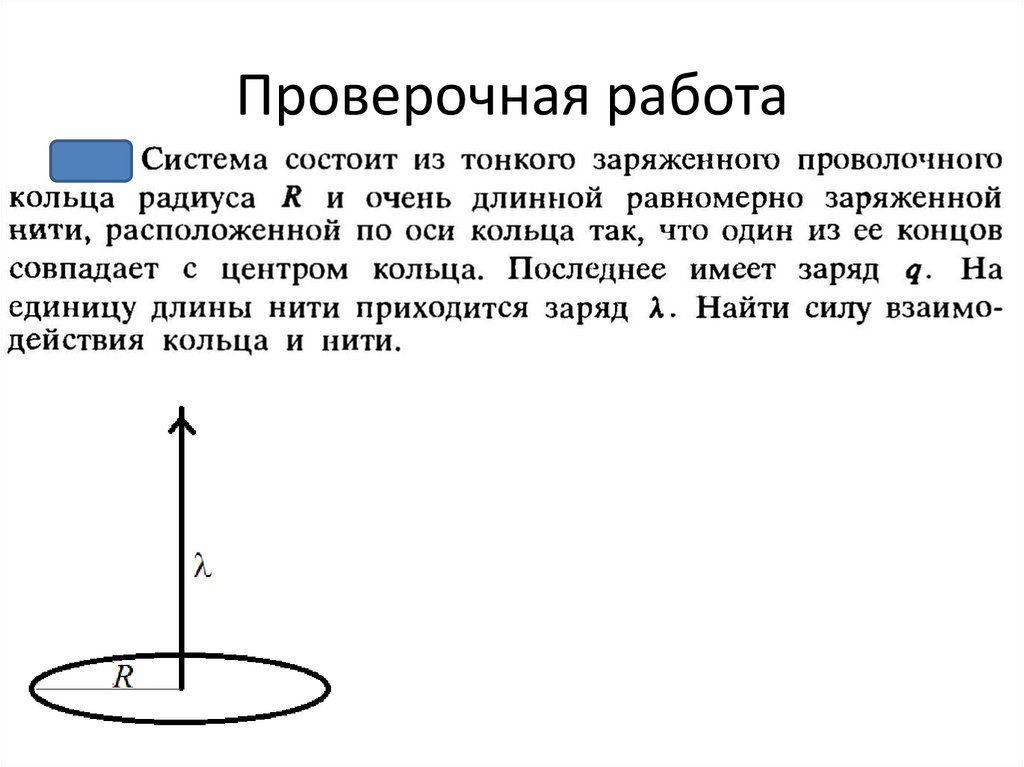
Проверочная работа3.
BrAB R cos , R sin , z ,
A R cos , R sin , 0
q
dq A
d
2
B 0, 0, z
kdq A
dE 3 rAB
rAB
2
kqd
kq
dEx
R cos Ex
R cos d 0
3
3
2 rAB
2 rAB 0
2
kqd
kq
dE y
R sin E y
R sin d 0
3
3
2 rAB
2 rAB 0
4.
2kqd
kq
kq
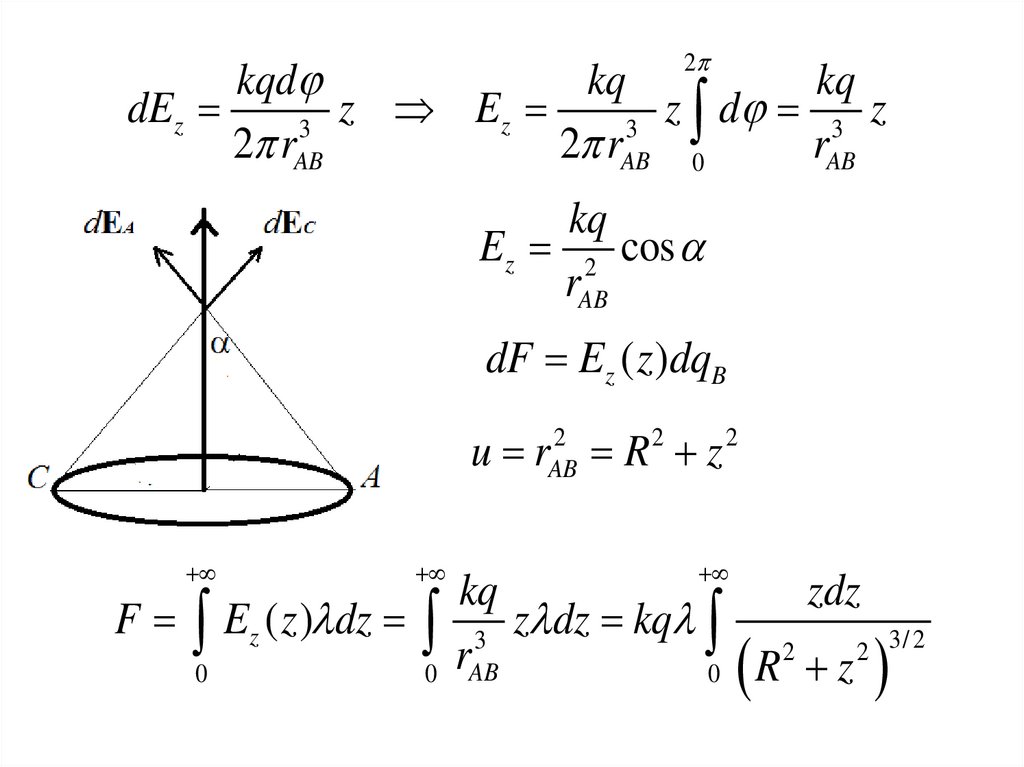
dEz
z Ez
z d 3 z
3
3
2 rAB
2 rAB 0
rAB
kq
Ez 2 cos
rAB
dF Ez ( z )dqB
2
u rAB
R2 z 2
F
E ( z) dz
z
0
0
kq
zdz
z dz kq
3/ 2
3
2
2
rAB
0 R z
5.
R2kq du kq 1/ 2
kq
F
2u
3/ 2
2 R2 u
2
R
6.
Операторq iqx jq y kqz
i j k
x y
z
q iqx jq y kqz
i j k
grad
x
y
z
7.
Дивергенция и роторa q qx ax q y a y qz az
ax ay az
div a a
x y z
i
j
k
q a qx q y qz
ax a y az
i
j
k
rota a
x
ax
y
ay
z
az
8.
Символический методdiv rota a a 0
rot grad 0
div(a b) a (a b) b (a b)
b a a a b b b rota a rotb
rot rota a ( a) a( a)
2
grad div a a
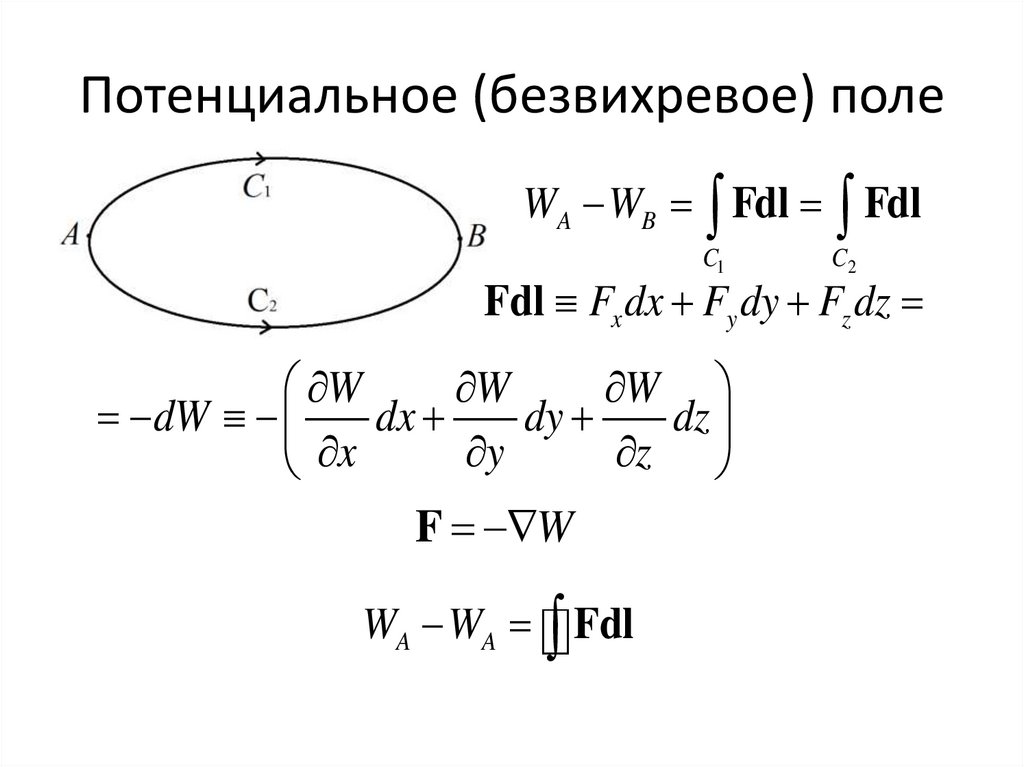
9.
Потенциальное (безвихревое) полеWA WB Fdl Fdl
C1
C2
Fdl Fx dx Fy dy Fz dz
W
W
W
dW
dx
dy
dz
y
z
x
F W
WA WA Fdl
10.
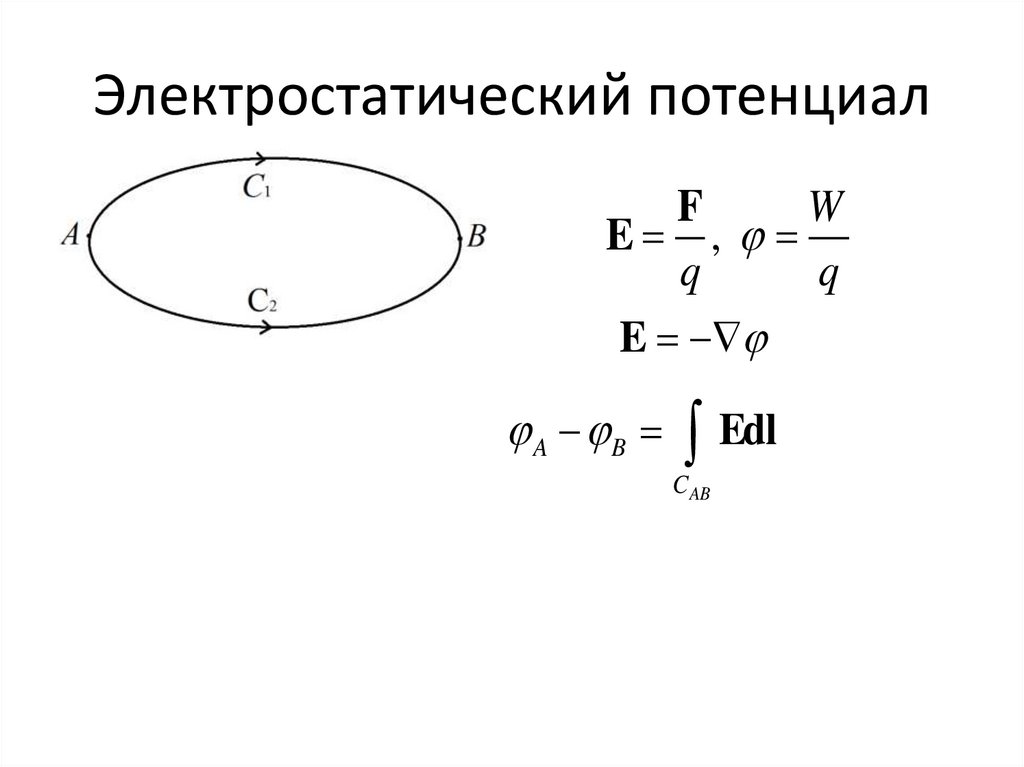
Электростатический потенциалF
W
E ,
q
q
E
A B
Edl
C AB
11.
Независимое определениеротора
rota lim
V 0
a dS
V
V
a dl
S
rota n lim
S 0
j
k
rota a
x
ax
y
ay
z
az
S
e
1
rota
a a
e
, , z :
i
ez
z
az
12.
Случай цилиндрической симметрии0,
0 :
z
e z a
az
rota
e
re
r sin e
1
rota 2
r sin r
ar ra
r sin a
er
r , , :
13.
Случай сферической симметрии0 :
e ra e ra
rota
r r
r r
14.
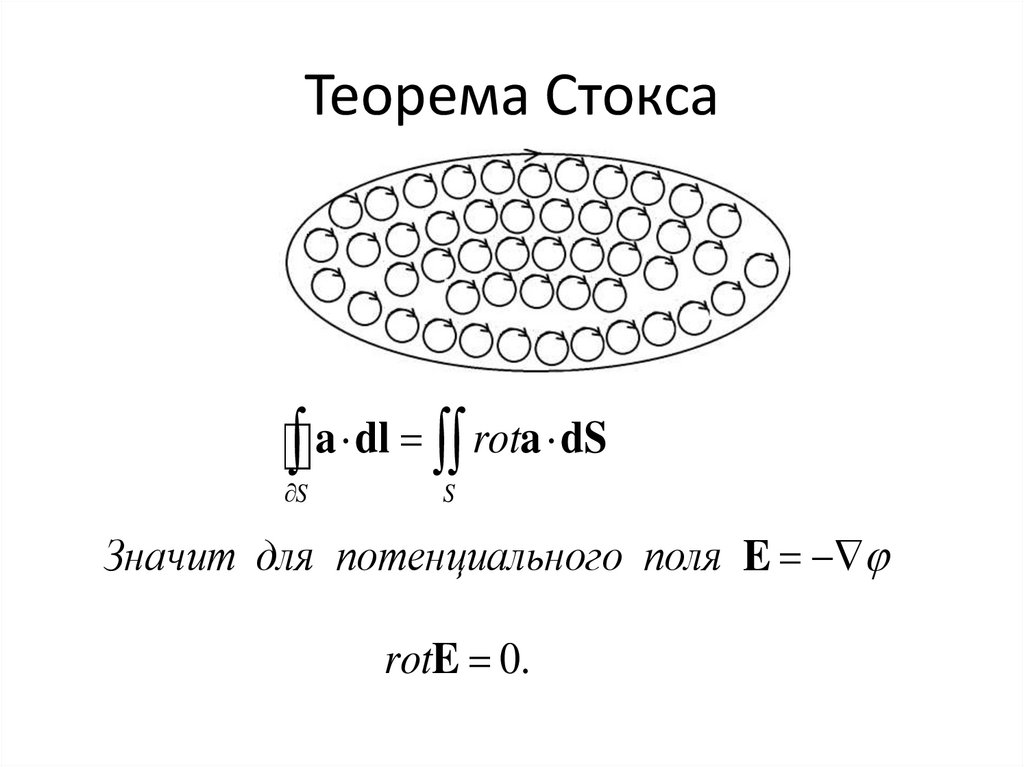
Теорема Стоксаa dl rota dS
S
S
Значит для потенциального поля E
rotE 0.
15.
Независимое определениедивергенции
ax a y az
div a
x y z
, , z :
diva lim
V 0
1 a 1 a az
diva
z
a dS
V
V
r , , :
1 r ar
1 sin a
1 a
diva 2
r
r
r sin
r sin
2
16.
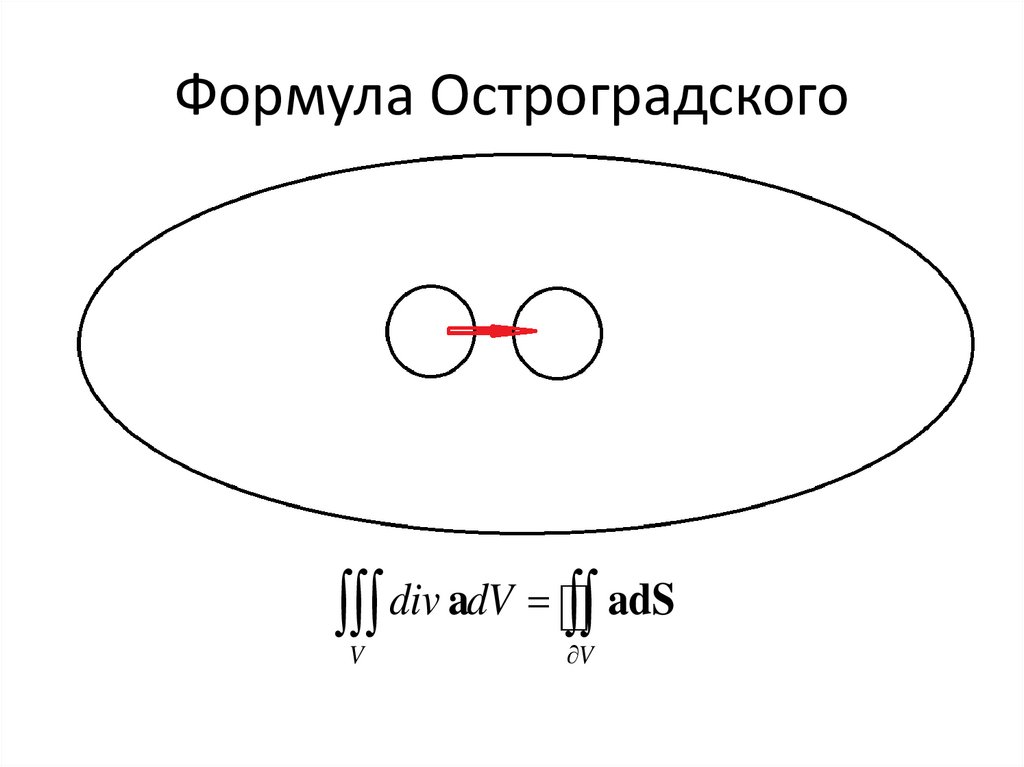
Формула Остроградскогоdiv adV adS
V
V
17.
Формулы Остроградского и Стоксаdiv adV adS
V
V
rota dS a dl
S
S
18.
Приецип суперпозицииE E1 E2 ...
Поле системы зарядов равно векторной сумме
полей подсистем.
Действует только в средах, в которых линейны
уравнения Максвелла.
Мы можем им пользоваться если исследуемые
поля много меньше внутриатомных
(макроскопические поля много меньше
микроскопических).
19.
Телесный уголТелесный угол измеряется отношением площади той
части сферы с центром в вершине угла, которая вырезается
этим телесным углом, к квадрату радиуса сферы:
dS0
dS cos r dS
d 2 sin d d
3 , dS ndS
2
r
r
r
20.
Теорема Гауссаq
rdS
q
q
E
d
3
4 0 S r
4 0
0
E
1
q
EdS dV
V
0
V
0
E
qr
4 0 r
3
21.
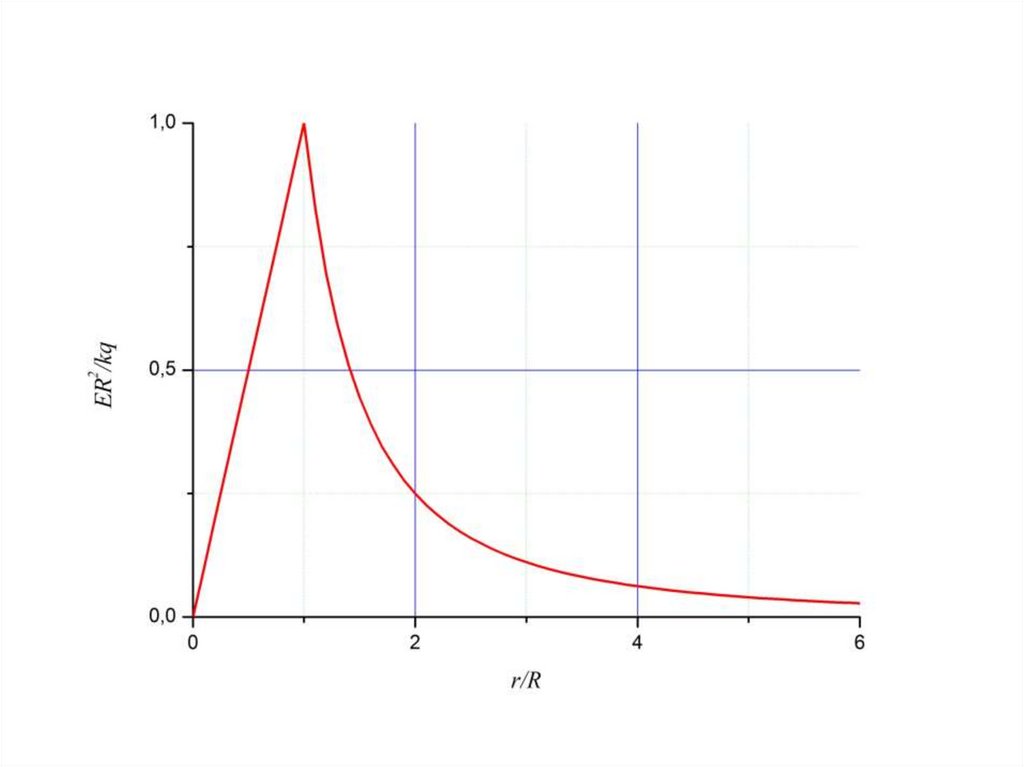
Поле равномерно заряженногошара
R, Q
E r R
E r R
E
1
q
EdS dV
V
0
V
0
22.
4 3r R : E 4 r E
r
3 0
2
4 3
Q
r
r
Q
3
4 3
3
R
0
R 0
3
r
E Q
4 0 R 3
3
r R : E 4 r E
2
Q
0
Q
E
2
4 r 0

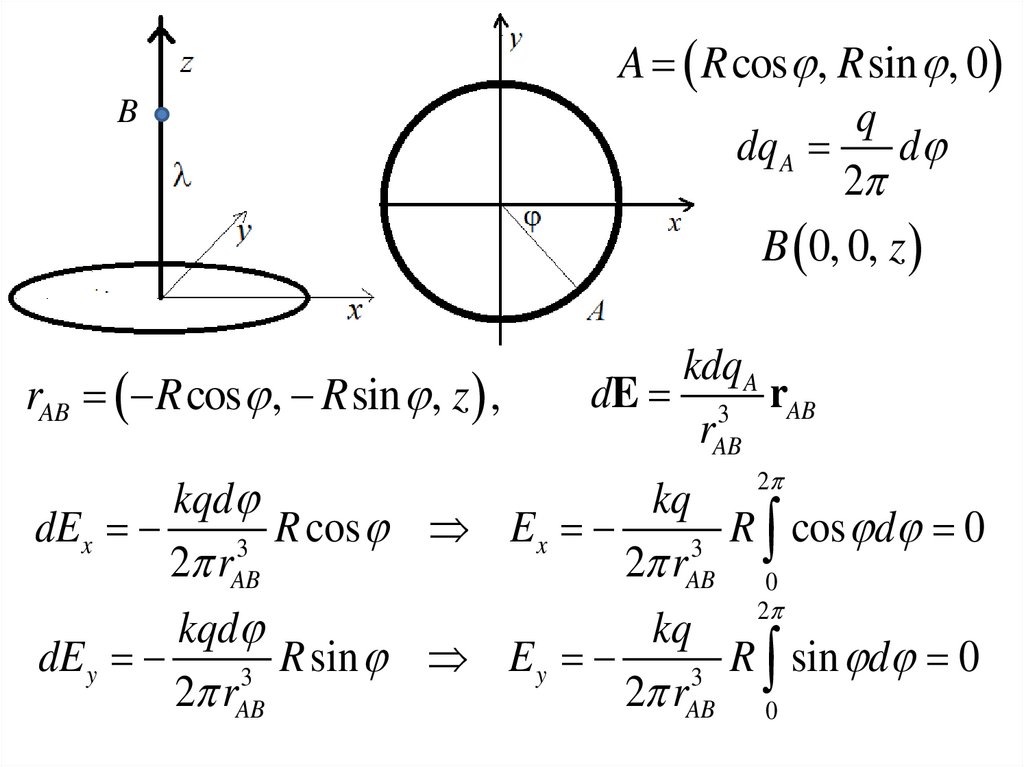













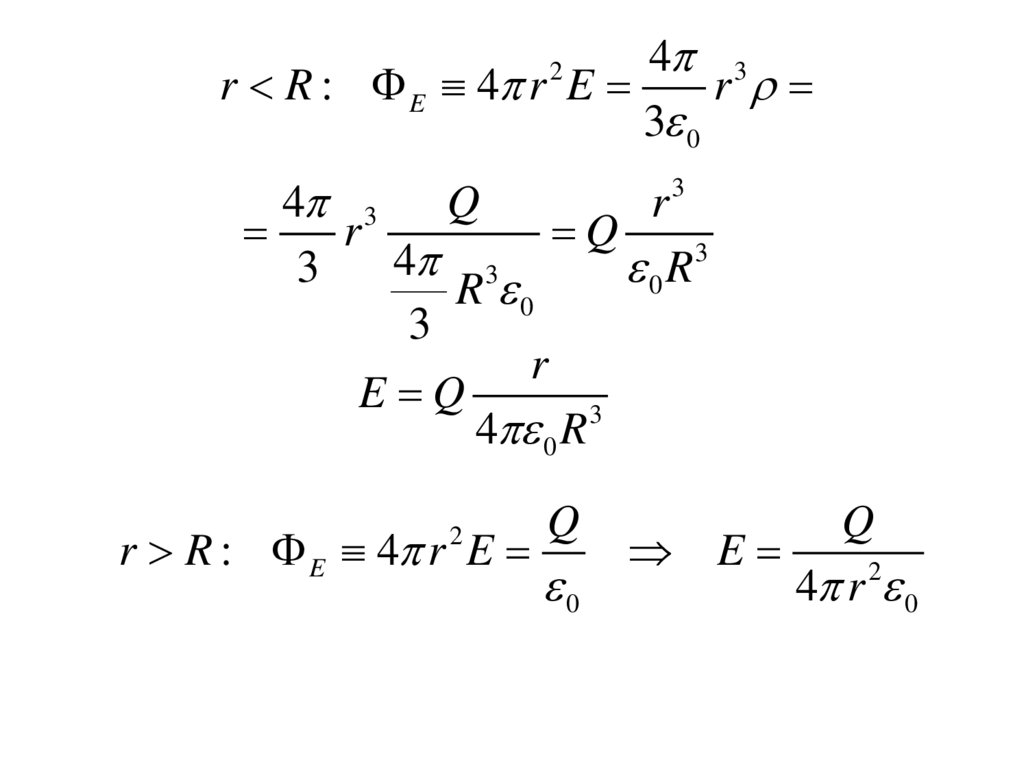
 physics
physics








